基于稀疏約束的DCD滑動窗RLS水聲信道估計算法研究
梁仕杰,王 彪,張 岑
(江蘇科技大學電子信息學院,江蘇鎮(zhèn)江212003)
0 引 言
水聲信道的多徑效應強、可利用帶寬窄,信號衰減嚴重等特點使得水聲通信的發(fā)展受到限制。利用水聲信道的稀疏性,研究稀疏信道估計算法可以極大地改善水聲通信的性能。
目前,稀疏信道估計問題一般通過壓縮感知算法[1-2]或自適應濾波算法來解決。基于壓縮感知的信道估計方法如正交匹配追蹤算法(Orthogonal Matching Pursuit, OMP),正則化正交匹配追蹤算法(Regularized Orthogonal Matching Pursuit, ROMP)等雖然可以根據(jù)少量的信息通過信號的重構(gòu)[3]來估計信道,但這些方法需要信道稀疏度的先驗信息[4],這限制了此類方法的應用。
自適應濾波算法主要有最小均方(Least Mean Square, LMS)算法、最小二乘(Least Square, LS)算法及遞歸最小二乘(Recursive Least Squares, RLS)算法等。LMS算法是基于均方誤差的算法,利用 LMS算法所估計的濾波器系數(shù)與數(shù)據(jù)的統(tǒng)計特性有關,因此其收斂速度較慢。而利用LS算法[5-6]估計信道,收斂速度較快。RLS算法在LS算法的基礎上引入了遺忘因子[7],雖然在一定程度上改善了LS算法的性能,但是其未對信道系數(shù)進行范數(shù)約束,因此在稀疏信道估計問題上效果并不好。文獻[8-9]將范數(shù)約束的概念引入到稀疏信道估計中,估計性能較傳統(tǒng)算法有明顯提高。本文在時域以高斯訓練序列為處理對象,在現(xiàn)有理論的基礎上,將懲罰函數(shù)加入到RLS算法的代價函數(shù)中,對估計信道系數(shù)進行范數(shù)約束,同時利用滑動窗方式處理代價函數(shù),在改善稀疏信道估計性能的同時又降低了 RLS算法的復雜度。此外,將二分坐標下降(Dichotomous Coordinate Descent, DCD)[10]算法應用于單次迭代代價函數(shù)最優(yōu)解的搜索中,進一步降低了算法的復雜度,對稀疏信道估計的研究具有一定的意義。
1 基于范數(shù)約束的DCD滑動窗RLS信道估計原理
1.1 信道估計問題的實質(zhì)
通信系統(tǒng)的接收信號在時域中表示為


1.2 RLS自適應濾波算法的原理
自適應濾波主要利用前一時刻獲得的濾波器參數(shù),根據(jù)估計誤差自動調(diào)節(jié)當前時刻的參數(shù),使得某個代價函數(shù)達到最小,從而實現(xiàn)最優(yōu)濾波。
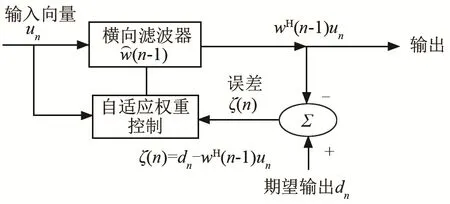
圖1 自適應濾波算法原理圖Fig.1 Schematic diagram of adaptive filtering algorithm
RLS自適應誤差算法的代價函數(shù)為
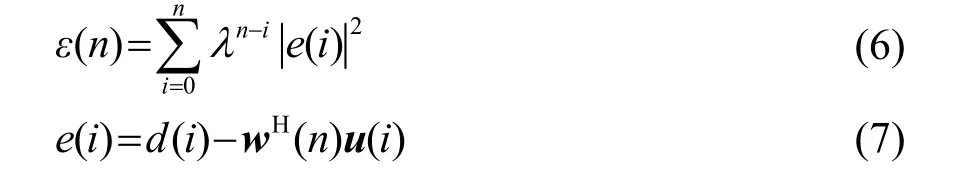
與LS算法相比,RLS算法引入遺忘因子,其作用是離當前時刻近的誤差賦較大權(quán)重,離當前時刻遠的誤差賦較小權(quán)重,從而減小過去較遠時間點的誤差影響,使濾波器平穩(wěn)工作。
1.3 基于范數(shù)約束的DCD滑動窗RLS算法原理



2 本文算法的信道估計步驟


3 仿真與分析
仿真所選信道為稀疏時不變信道,其時域信道沖激響應模型為

其中,L是具有不同時延的多徑數(shù)目,h(l)是第l條路徑下的信道增益,τl是第l條路徑下的時延差。
3.1 懲罰函數(shù)對估計結(jié)果影響
仿真采用的高斯訓練序列的長度為 7 000,信道采樣點數(shù)為 2 000,采樣頻率為 128 kHz。迭代5 000次,信噪比為25 dB。圖2是本文采用的DCD滑動窗-Lasso RLS算法估計結(jié)果、RLS算法估計結(jié)果以及實際信道系數(shù)的對比圖。由圖2可知,RLS算法與本文采用算法在信道的抽頭系數(shù)處估計精度相似,但是RLS算法估計結(jié)果在信道零系數(shù)位置處普遍存在波動,因而其對稀疏信道估計的結(jié)果較差。本文采用的算法利用Lasso懲罰函數(shù)對信道系數(shù)進行了l1范數(shù)約束,使稀疏信道估計精度更高。
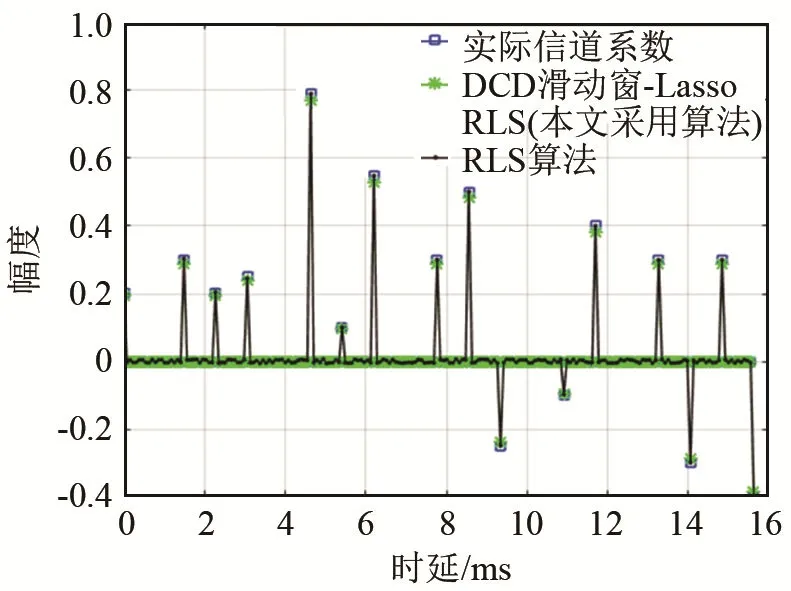
圖2 懲罰函數(shù)對估計結(jié)果的影響Fig.2 The effect of the penalty function on the estimated result
3.2 不同種類懲罰函數(shù)的估計性能對比
本節(jié)主要通過每次迭代所估計的信道系數(shù)與實際信道系數(shù)的歸一化均方誤差(Normalized Mean Square Error, NMSE)來反映各算法信道估計的性能。其數(shù)學表達式為
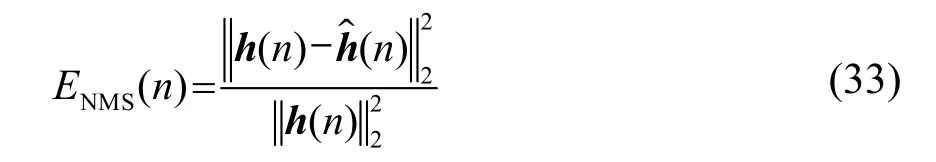
本部分對比了代價函數(shù)采用三種不同懲罰函數(shù)時的估計性能。高斯訓練序列長度為 7 000,信道采樣點數(shù)為2 000,迭代次數(shù)為5 000,信噪比為25 dB,結(jié)果如圖3所示。由圖3可見,經(jīng)過5 000次迭代,DCD滑動窗-Lasso RLS(套索懲罰函數(shù))算法的估計性能最好,這是因為它代價函數(shù)中的Lasso 懲罰函數(shù)用l1范數(shù)來約束信道系數(shù),將絕對值較小或影響因子較小的自變量的回歸系數(shù)置為 0,這使得它更適用于稀疏信道估計,DCD滑動窗-ElasticNet RLS(彈性網(wǎng)懲罰函數(shù))算法的β值為0.6,其性能介于 DCD滑動窗-Lasso RLS算法和DCD滑動窗-Ridge RLS(嶺回歸懲罰函數(shù))算法之間。
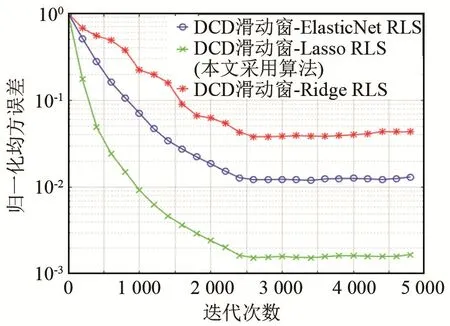
圖3 不同懲罰函數(shù)的估計性能對比Fig.3 Comparison of estimation performance between different penalty functions
3.3 不同信道估計算法的估計性能對比
本節(jié)分析了本文采用算法與傳統(tǒng)信道估計算法的性能。信噪比在 5~30 dB變換,變換間隔為5 dB。不同信道估計算法的歸一化均方誤差如圖4所示。在LS信道估計過程中,256個子載波每隔8個子載波插入導頻。OMP算法采用隨機導頻。RLS算法和DCD滑動窗-Lasso RLS算法均通過時域插入長度為1000的高斯訓練序列。由于OMP算法感知矩陣中的傅里葉變換矩陣列數(shù)與信道長度相同,若信道長度過大,將會大大增加仿真的復雜度,因此稀疏信道采樣點數(shù)取為100。由圖4可知,所有算法的歸一化均方誤差都隨信噪比的增加而下降,LS算法雖然簡單易實現(xiàn),但其估計精度遠低于其余三種算法。這是由于LS算法在估計稀疏信道時忽略了噪聲的影響,所以信道估計值對噪聲干擾的影響比較敏感。同時,由于LS方法的整體估計精度不高,因此其信道估計性能比較其他算法變化波動較小。RLS算法估計精度略優(yōu)于OMP算法,本文算法在四種信道估計算法中性能最優(yōu)。
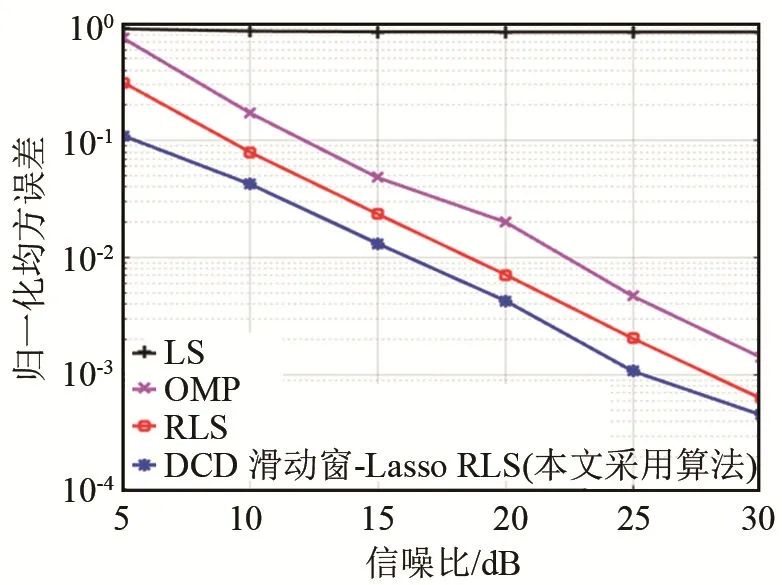
圖4 不同信道估計算法的歸一化均方誤差Fig.4 Normalized mean square error of different channel estimation algorithms
3.4 不同信道估計算法的復雜度對比
通過CPU運行時間分析不同信道估計算法的復雜度,結(jié)果如圖5所示,仿真信噪比為15 dB。基于壓縮感知的信道估計方法的迭代次數(shù)和稀疏度K值有關,因此OMP算法受K值的影響較大,K值越大,其復雜度越高。本文采用的DCD滑動窗-Lasso RLS算法與RLS算法相比,用滑動窗方法處理代價函數(shù)并且應用 DCD算法搜索其最優(yōu)解,減少了算法的復雜度。與LS算法相比,本文算法因在代價函數(shù)中添加了范數(shù)約束項,所以其復雜度略高于LS算法,但其信道估計精度遠高于LS算法。
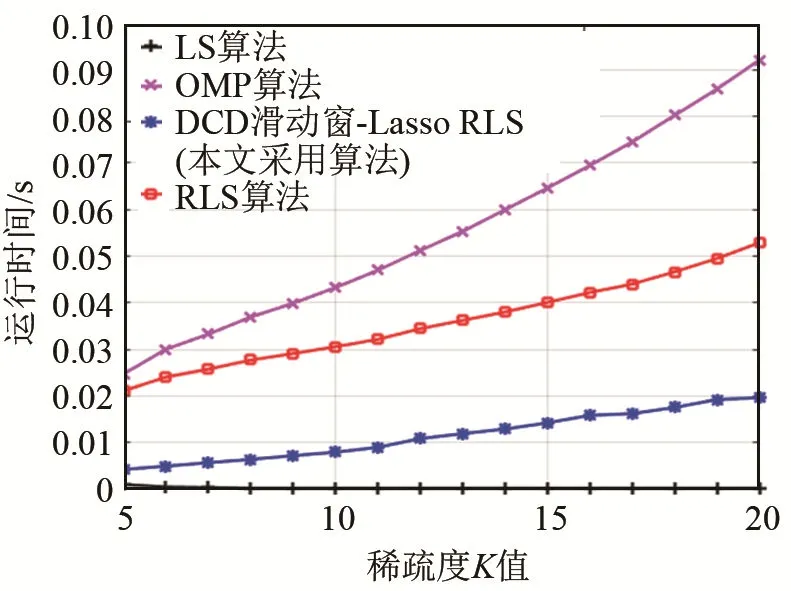
圖5 不同信道估計算法的CPU運行時間Fig.5 CPU running time of different channel estimation algorithms
4 結(jié) 論
本文提出了一種基于時域訓練序列的自適應稀疏信道估計算法。為解決傳統(tǒng)算法在稀疏信道估計方面精度低的問題,在經(jīng)典RLS算法的代價函數(shù)中添加了懲罰函數(shù)項,用以對信道系數(shù)進行范數(shù)約束。仿真結(jié)果表明本算法相較于傳統(tǒng)信道估計算法,提高了稀疏信道估計的精度。此外,所提算法在其代價函數(shù)中應用滑動窗處理方法并通過 DCD算法搜索代價函數(shù)的最優(yōu)解,仿真結(jié)果表明本算法相較于其他信道估計算法具有較低的復雜度。因此將本算法應用于稀疏信道估計中具有一定的意義。

