離散元法的螺旋攪拌機參數優化及其數據模型構建

（塔里木大學 機械電氣化工程學院，新疆阿拉爾 843300）

0 引言

顆粒物質超越了固、液、氣態的界限被視為第四態物質［1-3］，因其特殊性，不同顆粒混合過程也不相同。顆粒混合機是利用外力混合顆粒的裝置，但顆粒混合運動受到顆粒的物理特性、混合機構的結構和工藝參數等影響［4］，沒有一種混合機能混合所有顆粒。深入研究顆粒在混合機內的運動規律可為提升作業效率，提高混合質量，攪拌機械結構設計及優化帶來理論指導。因此，研究顆粒混合攪拌運動規律十分必要。

螺旋攪拌混合機的結構設計受到顆粒隨機運動和混合特性的影響。顆粒在混合攪拌機內的運動非常復雜，傳統通過試驗方法預測和評價混合過程，許多參數難以獲得［5-6］。隨著各學科的交叉滲透，計算機仿真模擬技術已成為探尋物體活動規律的主要研究方法。因為離散元法能形象的描述螺旋攪拌機內顆粒體系的運動規律及參數信息，所以受到了廣泛的應用。基于此，李斌［7］將DEM與計算流體力學相結合，對流化床內顆粒混合運動機制進行定性與定量分析，指出在模擬工況下，顆粒混合質量與流化氣速有關，且存在最佳流化氣速。徐穎［8］用離散元法模擬了紅外滾筒干燥機內顆粒混合運動，發現顆粒混合效果與初始分布有關。Shirsatha［9］采用三維粒子跟蹤測速的研究方法，得出了顆粒實際運動路線與離散元模擬的運動軌跡高度吻合。張凱杰［10］用離散元法模擬了不同轉速下回轉設備的運動，發現離散元法不僅可定量研究顆粒在空間中的運動，而且易于找出最佳轉速。郝友莉［11］用離散元法對粉體在不同振幅和頻率下的振動密實過程進行仿真，發現隨著振幅和頻率的增加，顆粒X方向上的速度波動變大，且振幅對顆粒速度波動的影響不顯著。基于DEM的螺旋攪拌機內糙米運動軌跡和混合過程很少有報道，但其研究結果可直接運用于實際生產中，所以具有重要的研究價值。

本文以自行設計的螺旋攪拌混合機為研究載體，采用離散元法的計算機仿真模擬數據進行數學建模，對螺旋攪拌機內糙米顆粒的運動過程做模擬研究，探究螺旋攪拌葉片轉速、填充量與顆粒混合程度的關系，為糙米攪拌混合機的設計和優化提供理論依據，也為其他橢球型顆粒混合運動規律分析提供參考。

1 離散元模型構建

1.1 糙米顆粒模型構建

模型使用的原顆粒聚合體建模方法能最大限度的模擬真實糙米顆粒［12-13］，本次試驗模型對經過一年貯藏，米粒飽滿，大小均勻的30粒新疆長粒糙米，采用千分尺進行測量，其中糙米長徑L范圍為 5.4～6.2 mm，短徑 P的范圍為 2.2～3.0 mm，試驗采用其平均值L=5.8 mm，P=2.6 mm。

1.2 螺旋攪拌混合倉模型建立

實際試驗的螺旋攪拌機如圖1所示，整個機器由進料口、攪拌混合倉、螺旋攪拌葉片、卸料口、以及與螺旋攪拌葉片相連的行星減速裝置等組成，其動力裝置采用750 W步進電動機可對轉速精確的調控，為了試驗取樣在螺旋攪拌倉的上方開有折疊式觀察口，以便于觀察糙米混合過程中運動狀態及取樣。

圖1 螺旋攪拌混合機Fig.1 Spiral mixer

螺旋攪拌混合倉由殼體和螺旋攪拌部件組成，殼體呈倒金字塔形并帶有進料口和出料口，仿真時為提升EDEM軟件效率只保留殼體部分，螺旋攪拌部件由一根軸和螺旋形葉片組成，螺旋葉片寬度為7.5 cm、厚度為0.5 cm、螺旋間距為18 cm。螺旋葉片表面光滑，以防止糙米顆粒黏連，螺旋攪拌混合倉模型材料選用鋼，用Solidworks2017繪制。

1.3 模擬參數確定

試驗采用貯藏一年后的新疆長粒糙米作為EDEM仿真軟件的橢球顆粒原型，因原顆粒較干燥，故忽略顆粒之間的粘附力和液橋力，選用Hertz-Mindlin（no slip）無滑動接觸模型作為橢球顆粒與橢球顆粒以及橢球顆粒與螺旋攪拌混合倉壁之間的接觸模型，其模型符合顆粒Hertz法向接觸理論和Mindlin-Deresiewicz切向接觸理論，顆粒在螺旋攪拌混合機內的移動和滾動符合平動方程和轉動方程。如式（1）和式（2）表示［14］：

式中 v ——顆粒平移速度，m/s；

I ——轉動慣量，kg·m2；

ω ——顆粒轉動速度，rad/s；

t ——為顆粒運動時間，s；

ni——與顆粒i接觸的顆粒總數；

Fn——顆粒間法向碰撞接觸力，N；

Fnd——法向阻尼，N；

Ft——顆粒間切向碰撞力，N；

Ftd——切向阻尼，N；

Tt——顆粒單元 i受到切向力矩，N·m；

Tr—— 顆粒單元 i受到滾動摩擦力矩，N·m；

g ——重力加速度，m/s2；

mi——顆粒 i質量，kg。

糙米之間相互碰撞的參數、糙米與攪拌倉內機壁碰撞的參數、糙米泊松比與密度等建模所需要的參數均參照胡國明的研究。

2 糙米顆粒運動軌跡分析

研究中轉速和填充率為自變量，變異系數為因變量，用離散元法分析了攪拌機內糙米的運動軌跡。其中，順時針旋轉攪拌機葉片，顆粒在螺旋攪拌混合機的混合運動無序且復雜。為更好地觀察到糙米顆粒在螺旋攪拌混合機的混合狀態，如圖2（a）所示，將物理參數完全相同的糙米顆粒群分為數量相同的上下兩層，上層標記為淺（青）色，下層標記為深（紅）色。如圖2（b）所示，在經歷了螺旋攪拌混合機的混合之后，兩種顆粒均勻的分布到螺旋攪拌混合倉內。

圖2 糙米狀態圖Fig.2 Brown rice status map

2.1 單一顆粒混合分析

如圖3所示，為探究糙米在攪拌機內的混合狀態，隨機從顆粒群中挑選出一顆糙米顆粒并在EDEM軟件中標記其運動軌跡。

在實施會計集中核算的時候，會計業務的決策者與執行者是相分離的，財務審批與會計監督之間的分離會改變單位的核算權以及會計監督權。審計部門與被審計單位之間的中間人就是核算中心，因此在會計監督工作中會存在著一些盲點。一旦會計財務處理出現了差錯、單位會計信息失真等問題，被核算單位認為本單位缺乏專業的會計人員，因此他們不會承擔相應的責任。所以在追究會計責任的時候，無法確定雙方的責任，增加了認定責任的難度。

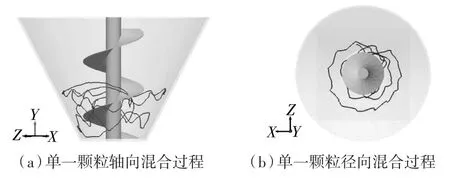
圖3 單一顆粒混合過程分布圖Fig.3 Distribution map of single particles

圖3（a）中該顆粒從軸向觀察大致呈螺旋狀沿螺旋攪拌軸轉動，在軸的四周無規律的運動著。圖3（b）從徑向觀察該顆粒發現其運動軌跡就像水中的波紋一樣，從螺旋攪拌軸向著四周擴散。綜合來看，顆粒在螺旋攪拌混合機內的軌跡近似橢圓形繞著軸運動，運動軌跡隨機且復雜，但又有規律。這是因為螺旋攪拌混合機特殊的攪拌裝置，螺旋攪拌葉片可以自下而上輸送糙米顆粒，且糙米顆粒在離心力的作用下輸送到螺旋葉片的邊緣后，被拋送到顆粒群中，最終在糙米間的擠壓力、摩擦力、自身的重力等多種作用力的共同作用下完成混合運動。從單顆粒在螺旋攪拌混合機內的運動軌跡可以看出：糙米顆粒在螺旋攪拌機內隨機運動明顯，在徑向和軸向上顆粒的混合運動活躍，混合效果明顯。

2.2 顆粒群運動分析

為了形象地表示顆粒群在攪拌機內的混合過程，試驗截取了顆粒從分層狀態到混合狀態軸向和徑向兩個方向具有代表性的宏觀運動矢量圖。

圖4 顆粒群軸向混合過程Fig.4 Axial mixing process of particle groups

如圖4（a）所示的顆粒群混合運動軸向第一形態，此時處于上層右側的淺色顆粒群沒有被螺旋攪拌葉片帶動做圓周運動，且部分的淺色顆粒擴散到深色顆粒群中，這一特征符合McCarthy描述的符合顆粒間擴散混合運動，即顆粒之間在運動中的相互滲透與貫穿。這種情況可能是因為靠近倉壁位置的淺色顆粒受葉片的作用力弱，在自重與上層顆粒擠壓力的共同作用下造成這一狀態；圖4（b）在螺旋攪拌葉片的提升作用下，深色顆粒被自下而上的帶動到淺色顆粒群中，且深色顆粒空出的位置快速的被重力作用下的淺色顆粒填充，淺深顆粒相互穿插；圖4（c）淺深顆粒在螺旋攪拌葉片的進一步作用下進行同向運動，處于右側的部分淺深顆粒滯留在倉壁處，造成這一原因可能是被螺旋攪拌葉片甩出的顆粒給倉壁處顆粒群施加了一定的擠壓力：圖4（d）隨著顆粒間混合運動的深入，顆粒速度之間的差異開始顯現，外在表現為淺深顆粒間明顯的剪切運動。其實，糙米顆粒在攪拌機內，擴散、穿插、剪切、下落，同向運動始終存在著。

圖5（a）為混合運動徑向第一形態，淺深顆粒在螺旋攪拌葉片的作用下開始運動；圖5（b）下層的深色顆粒隨著螺旋攪拌葉片上升，并由于向心力不足無法維持圓周運動開始朝著四周擴散；圖5（c）深淺顆粒在混合過程中，由于受到螺旋攪拌葉片的作用力，顆粒之間的擠壓力的大小不同造成速度分化，表現為局部穿插效果明顯。圖5（d）是顆粒混合過程的完全擴散階段，可以看出深色顆粒已經充分的穿插滲透到淺色顆粒中，且呈流線狀繼續與淺色顆粒混合。直至分布均勻。

3 螺旋攪拌機混合試驗的模型建立與驗證

3.1 試驗安排

為定量描述螺旋攪拌混合機內糙米顆粒混合程度，運用變異系數評價顆粒混合程度。利用EDEM的后處理手段將螺旋攪拌混合機混合區域進行網格劃分，通過統計三維網格中帶色糙米的數量（剔除處于混合倉外邊緣及上方的網格），根據下式計算其變異系數RCV：

式中 Sd—— 劃分網格中紅色糙米顆粒個數的標準差；

Mn—— 劃分網格中紅色糙米顆粒個數的平均值。

3.2 仿真結果的分析與數據模型構建

如圖6、圖7所示，通過離散元法對糙米在攪拌機內的混合過程進行仿真模擬，可發現轉速、填充量對變異系數的影響規律，發現當填充量一定時，隨著轉速的提高，螺旋攪拌混合機的變異系數越低，原因為在相同時間內，轉速越高使得螺旋攪拌混合機內螺旋葉片與顆粒之間的接觸增多，混合效果好。當轉速一定時，發現填充量為35.13%與48.49%的變異系數較低，填充量為42.82%時變異系數較高，即混合效果差，是因為填充量較少的情況下，螺旋攪拌葉片與糙米之間的接觸更充分。當填充量大時，因為填充量的增多，造成染色顆粒與未染色顆粒之間的接觸面積增加，推動了各層顆粒之間的位置互換。

圖6 轉速影響下變異系數擬合曲線（試驗1）Fig.6 Fitting curve of variation coefficient under the influence of rotational speed（Test 1）

圖7 填充量影響下變異系數擬合曲線（試驗2）Fig.7 Fitting curve of variation coefficient under the influence of filling amount（Test 2）

應用SigmaPlot軟件擬合轉速與變異系數仿真值的數學關系，擬合曲線為圖6所示，擬合數學模型為：

式中 RCV——變異系數，%；

n ——轉速，r/min；

P1、P2——模型系數，其中 P1=43.441 1，P2=0.012 9。

對轉速與變異系數仿真值擬合后可發現方程的決定系數R2=0.995 0，方程擬合度較高，表明該數學模型可以代表此次模擬轉速與變異系數的關系。

應用SigmaPlot軟件擬合填充量與變異系數仿真值的數學關系，擬合曲線為圖7所示，擬合數學模型為：

式中 RCV——變異系數，%；

φ——填充量，%；

P1、P2、P3—— 模型系數，其中 P1=10.127 2，P2=8.334 1，P3=42.682 1。

對填充量與變異系數仿真值擬合后可發現方程決定系數R2=0.976 2，方程擬合度較高，表明該數學模型可以代表此次模擬轉速與變異系數的關系。

3.3 驗證數據模型

按照試驗設計，可分別得到轉速、填充量與變異系數的數據如表1與表2所示，可發現實際試驗中變異系數略大于數據模型模擬的變異系數。考慮到糙米在螺旋攪拌混合機實際工作中影響因素較多，采用SigmaPlot軟件擬合的數據模型是可接受的，基本符合實際情況。

分析轉速與變異系數的關系時可發現，變異系數試驗值與數據模型模擬的變異系數仿真值對比誤差最大7.6%，最小3.4%，如表1所示，由此可表明模型效果良好。

表1 仿真變異系數與試驗值對比（試驗1）Table 1 Comparison between simulated variation coefficient and experimental value（Test 1）

分析填充量與變異系數的關系時可發現，變異系數試驗值與數據模型模擬的變異系數仿真值對比誤差最大5.8%，最小2.9%，如表2所示，由此可表明模型效果良好。

表2 仿真變異系數與試驗值對比（試驗2）Table 2 Comparison between simulated variation coefficient and experimental value（Test 2） %

上述模型的建立有助于分別詳細的表明轉速、填充量與變異系數的關系，為后續其他轉速，填充量的試驗提供理論參考依據，具有重要研究價值。

4 結語

試驗采用離散元法模擬了攪拌機內糙米顆粒的運動軌跡。從單顆粒的隨機運動和顆粒群的混合運動兩方面分析了顆粒的運動規律和混合特性，發現糙米在攪拌機內隨機運動顯著，軸向上、徑向上的運動十分活躍。填充量在35.13%與48.49%時，混合效果比42.82%的混合效果更優，變異系數的數學模型預測值與實際試驗值誤差在2.9%～5.8%之間，驗證了該數學模型具有良好的準確性，該研究降低了實際生產中螺旋攪拌機能耗的損失，提升了糙米的攪拌效率，節省能源，提高了螺旋攪拌機的工作效率，具有重要的工藝研究價值。