基于動力數值分析的拋錨航速
吳衛兵
(大連海事大學 航海學院, 遼寧 大連 116026)
挪威和德國勞氏船級社(Det Norske Veritas Germcunischer Lloyd, DNV GL)調查數據[1]顯示每年千艘船舶丟錨事故數為8~10起,其中油船、化學品船和客船占比較高。由于錨泊操作不當導致的事故占錨泊事故總數的20%以上,拋錨的航速控制不當是錨泊事故發生的主要原因之一。拋錨時船舶的動能應會被船體受到的風阻力、水流阻力以及錨鏈的拉力做功抵消,如拋錨航速太快則會導致拖錨,或者錨、錨鏈和錨機等設備的損壞,嚴重時可能會導致發生擱淺、碰撞和人員傷亡等事故。顯然,拋錨航速越小,越利于保護錨設備。但拋錨航速太小將使操縱船舶到拋錨位置的難度加大,并且拋錨時還有可能使錨鏈在海底堆積,嚴重時會出現錨與錨鏈絞纏的現象。因此,拋錨航速是判斷錨泊作業安全的一個重要參數。目前,錨泊操縱運動數學模型、船舶拋錨作業和錨泊操縱的方法等相關研究較多,如:王飛[2]建立用于預報分析船舶在錨泊操縱全過程中各種動態運動響應的船舶錨泊操縱運動數學模型,并設計一種錨抓力的數學計算模型;巖井聰[3]利用動能定理構建船舶受力、位移、船舶質量以及航速之間的數學關系模型;顧明章[4]提出大型集裝箱船舶進拋法定點錨泊操縱的方法;富志禹等[5]運用牛頓力學定律描述船舶拖錨淌航的過程,并計算船體阻力和附加慣性力;陸冬青等[6]提出錨在海底移動的運動方程,并在考慮錨在海底移動的距離、錨桿仰角、錨型和底質等因素的基礎上,計算錨的運動和船體的運動態勢,建立了一種基于船舶操縱運動數學模型研究小組(Ship Manoeuvring Mathematical Model Group, MMG)模型建立船舶拋起錨操縱運動數學模型; MCDOWALL[7]在總結航海實踐中大型船舶拋錨經驗的基礎上,運用牛頓力學定律和能量守恒定理建立大型船舶拋錨的運動數學模型,將船舶余速所致的動能分解成艏艉和正橫2個方向上外力做功的矢量和,并分別進行計算出大型船舶拋錨航速的推薦值;唐天國[8]在流體動力學原理的基礎上,建立艦船錨泊運動的動力學模型和非線性波浪力的數學模型,并對艦船錨泊運動和六自由度操縱運動進行研究。目前,專門針對拋錨航速的定量研究相對較少,在航海實踐中主要依靠經驗數據作為支撐。因此,有必要對拋錨航速進行定量研究,在參考船舶動能定理模型的基礎上,綜合考慮錨在觸底至抓牢過程中,做功對船舶動能的消耗和錨機設計的剎車力,選取小型、中型、大型和超大型等4種實船船型參數進行計算,并將計算值與經驗值進行比較分析,最后建議各種船型的拋錨航速,以便在航海實踐中拋錨作業時提供參考。
1 拋錨航速與錨鏈受力關系數學模型
當錨觸底并抓牢不再移動時,拋錨時船舶余速所產生的動能應等于船體受到的外力做功之和。這些外力包括錨鏈張力、船體受到的水流阻力和風阻力。按照良好船藝的要求,拋錨前將調整船舶航向至頂風頂流方向。根據文獻[3]提出的船舶動能定理船舶拋錨前余速所致的動能與外力做功關系為
(1)
式(1)中:Fw為船舶受到的風阻力,N;FV為船體受到的水阻力,N;FA為錨鏈張力,N;SV為拋錨至停船時船舶前進的水平距離,m;SA為錨觸底至抓牢時移動的水平距離,m;MV和ME分別為船舶質量和附加質量,ME=0.1MV,kg;v為船舶拋錨時船舶的對地航速,m/s。
根據《港口工程荷載規范》[9]計算船舶受到的風阻力和水流阻力。
1.1 風阻力
(2)
(3)
式(2)和式(3)中Fxw和Fyw分別為風阻力的橫向和縱向分力,kN;Axw和Ayw分別為橫向和縱向受風面積,m2;Vxw和Vyw分別為風速的橫向和縱向分量,m/s;ζ1和ζ2分別為風壓不均勻折減系數和風壓高度變化修正系數,其取值見表1和表2。Fw應為Fxw和Fyw的合力,當船舶頂風拋錨時,風阻力Fw=Fyw。
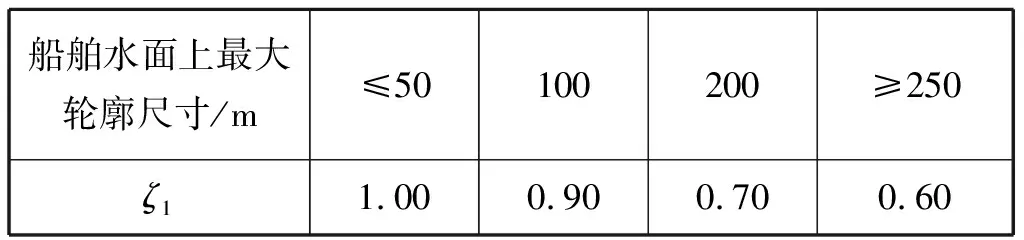
表1 風壓不均勻折減系數[9]

表2 風壓高度變化修正系數[9]
1.2 水流阻力
拋錨時航速一般較小,興波阻力和渦流阻力也很小,因此,船體受到的水流阻力主要考慮黏性阻力為
(4)
式(4)中:FV為水流黏性阻力,N;ρ為水密度,kg/m3;AV為船舶吃水線以下的表面積,m2;vTW為船舶對水航速,為實際對地航速與流速的矢量差,當船舶頂流拋錨時,vTW則為拋錨航速v與流速的代數和,m/s;Cv為水流縱向分力系數。
Av的計算為
Av=1.7LD+CbLB
(5)
式(5)中:L為船長,m;D為船舶吃水,m;B為船寬,m;Cb為方形系數。
水阻力系數計算為
CV=0.046Re-0.134+b
(6)
(7)
式(7)中:Re為水流對船舶作用的雷諾數;b為系數;v1為水的運動黏性系數,與水溫有關。
2 拋錨工況及參數取值
2.1 拋錨場景設置
選取小型、中型、大型和超大型等4種實船船型參數進行計算。小型船參數采用某3 000噸級的集裝箱散貨兩用船,中型船參數采用某1.8萬噸級靈便型散貨船,大型船舶參數采用某82 000tDW巴拿馬型散貨船,超大型船采用某超大型油船(Very Large Grude Carrier, VLCC)船型實船參數。選擇計算船型尺度及其相關參數見表3。
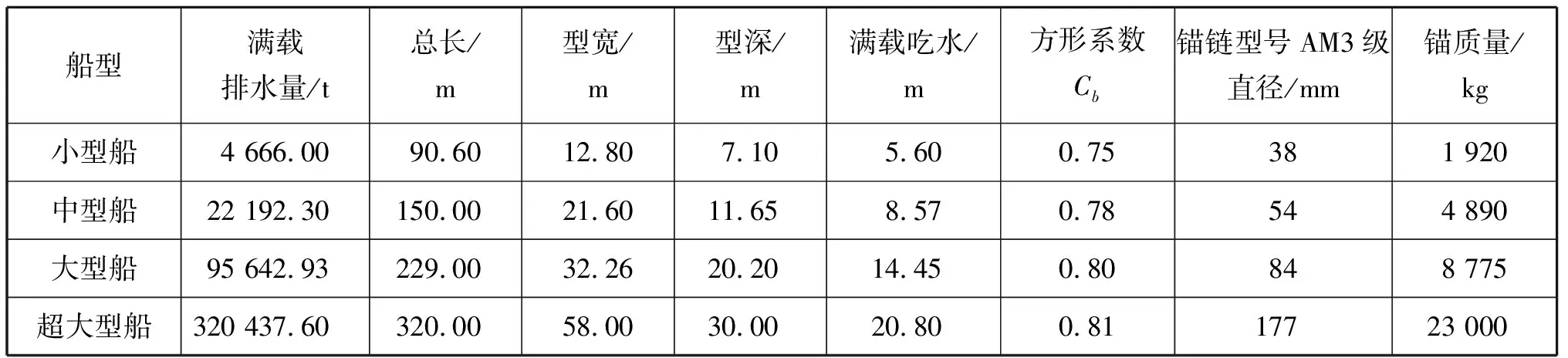
表3 選擇船型尺度及其相關參數[10-12]
錨泊水域按照一般港口水域錨地設置,選取錨地水深小型船舶20 m,其他船型30 m,底質良好,錨觸底后移動10 m(SA,約5倍錨桿長度)抓牢。[10]
在出鏈長度為3節(82.5 m)錨鏈、4節(110.0 m)錨鏈、5節(137.5 m)錨鏈和6節(165.0 m)錨鏈等4種工況下,分別計算在不拖錨和不損壞錨設備時的拋錨航速極限值。
在航海實踐中主要有退速拋錨和進速拋錨2種拋錨方式。相較退速拋錨方式進速拋錨具有便于控制錨位和拋錨作業耗時短等優點,因此在航海實踐中被廣泛采用。在退速拋錨過程中,需倒車至停船后繼續倒車船舶才會出現退速,控制到較小的退速拋錨相對較易。船舶因退速太快而導致拋錨事故情況非常少見。因此,選取對控制拋錨航速有較大難度的進速拋錨方式進行數值計算。風阻力做功遠小于水阻力做功,因此,計算過程忽略風的影響,船舶頂流拋錨時實際控制的拋錨航速等于不考慮在水流影響情況下的計算拋錨航速值與水流速度值的代數和。綜上所述,計算拋錨航速極限值時選擇無風流水域。
2.2 SV和SA取值
對應上述4種工況下船舶的水平位移量SV為
(8)
式(8)中:LA為出鏈長度,m;DW為水深,m。
代入數值計算在4種計算工況下的船舶水平位移量SV值分別見表4和表5。

表4 小型船舶的SV值 m

表5 中型、大型和超大型船舶的SV值 m
2.3 b和v1取值
b和v1的插取值見表6和表7。
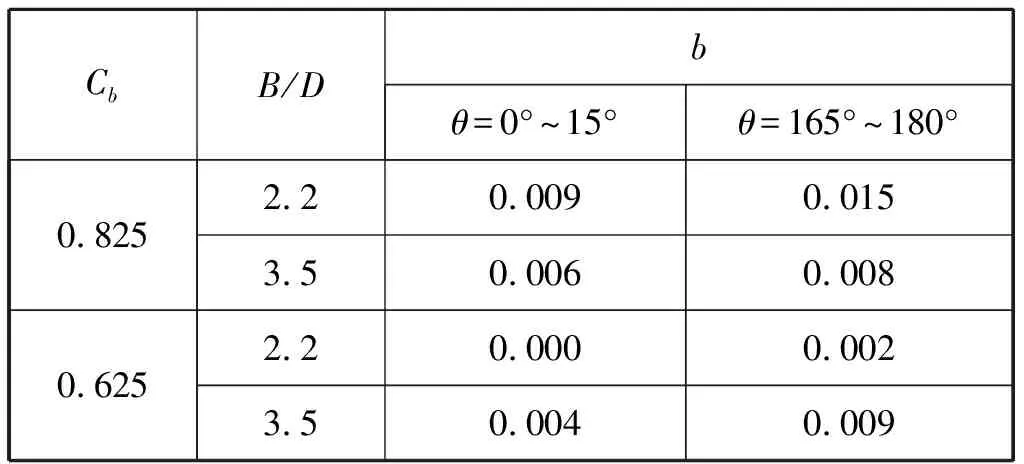
表6 b取值表[9]

表7 v1取值表[9]
表6和表7中:D為船舶吃水,m;B為船寬,m;θ為水流方向與船舶縱軸之間的夾角,(°);油船、散貨船和河駁的Cb取0.825;雜貨船、河船的Cb取0.625。
綜上,在水溫15℃時v1取1.14×10-4m2/s;選擇計算小型、中型、大型和超大型船舶的b分別為0.002 4、0.013 3、0.014 8和0.011 8。
3 錨機剎車力與錨抓力
中國船級社《鋼制海船入級規范》[14]規定:設置有止鏈器的錨機剎車力不應小于錨鏈破斷負荷的45%,錨鏈破斷負荷按照《電焊錨鏈》(GBT549—2017)[15]查取。選擇計算的小型、中型、大型和超大型船舶的錨鏈分別為AM3級直徑38 mm、54 mm、84 mm和177 mm,錨鏈的破斷負荷分別為1 160 kN、2 270 kN、5 160 kN和9 290 kN;所對應船型的設計錨機的剎車力應該不小于522.0 kN、1 021.5 kN、2 322.0 kN和4 180.5 kN。
錨抓力與底質、錨的類型和錨重等有關。設定泥沙底質,錨抓力與錨鏈長度和水深的關系表見表8。
鏈長與水深比為2.75時,選擇計算船型的錨抓力為1.8倍水中錨重,則錨抓力分別為45 kN、75 kN、135 kN和353 kN。
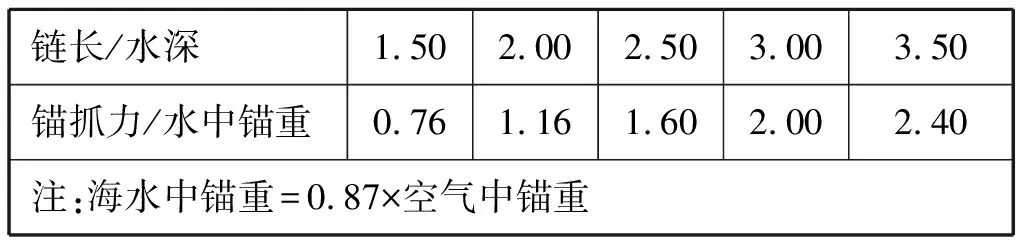
表8 錨抓力與錨鏈長度和水深關系表[12]
顯然選擇計算船型的設計錨機剎車力明顯大于錨抓力,船舶在拋錨時,因航速太快首先將導致拖錨,之后有可能發生損壞錨機剎車的情況。因此,如拋錨時要求相對準確的錨位,不出現拖錨現象,則FA應不大于PA,即FA≤PA;如拋錨有協助減速的目的但要求不應損壞錨機剎車,則FA應不大于PW,即FA≤PW。綜上,只需針對FA=PA和FA=PW2種臨界狀態進行計算,即可獲取拋錨航速的2個臨界值,分別為不發生拖錨現象和不損壞錨機時的航速最大值。選擇計算船型的PA和PW值見表9。
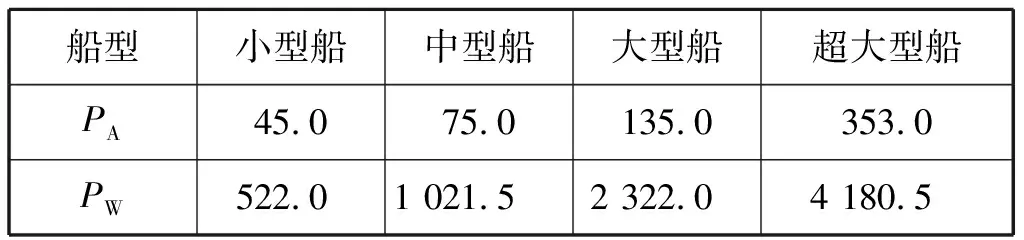
表9 PA和PW值 kN
4 數值計算與分析
4.1 計算結果
分別計算在出鏈長度為3節、4節、5節和6節錨鏈等4種工況下錨鏈張力與拋錨航速的關系,并計算當錨鏈張力FA分別為PA和PW時的拋錨航速值。計算結果見圖1~圖4。
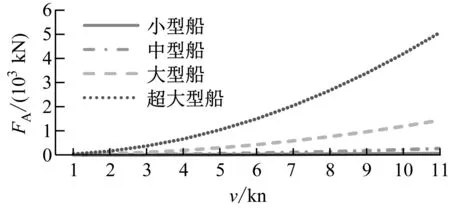
圖1 工況1計算結果(3節錨鏈)
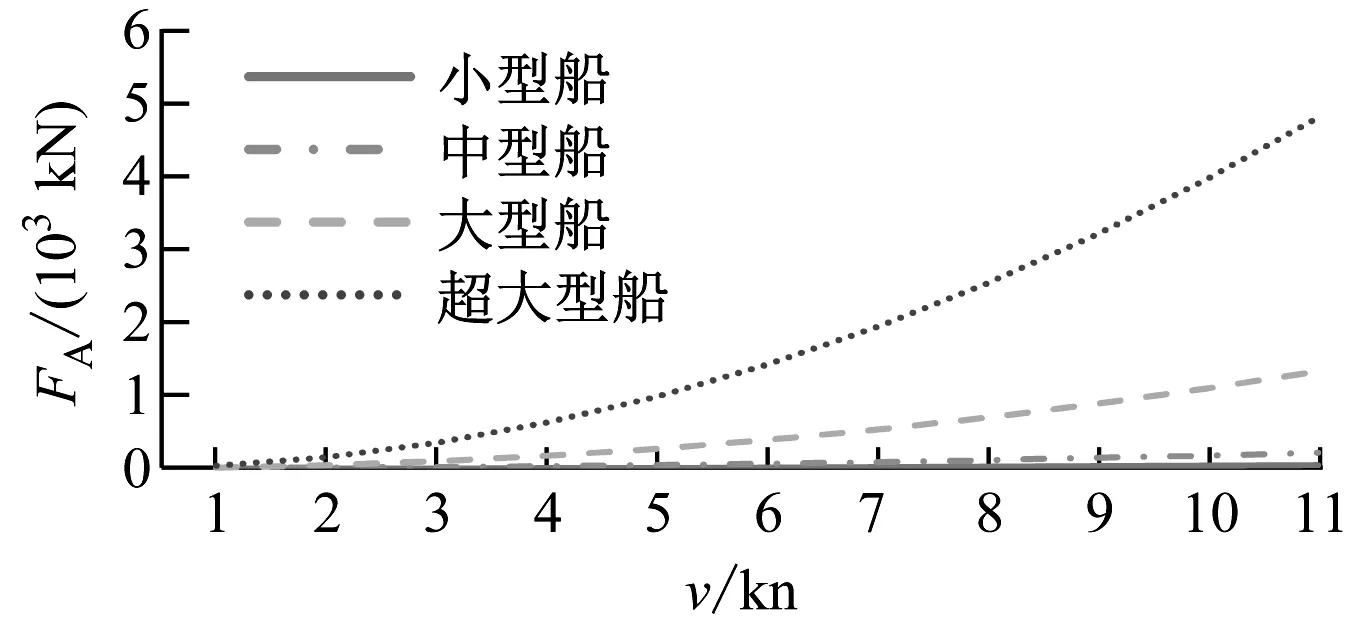
圖2 工況2計算結果(4節錨鏈)
4.2 數值分析
分析計算結果可知:
1)相同的v,船舶排水量越大,FA越大。隨著v的增加,排水量越大的船舶,FA增加越明顯。
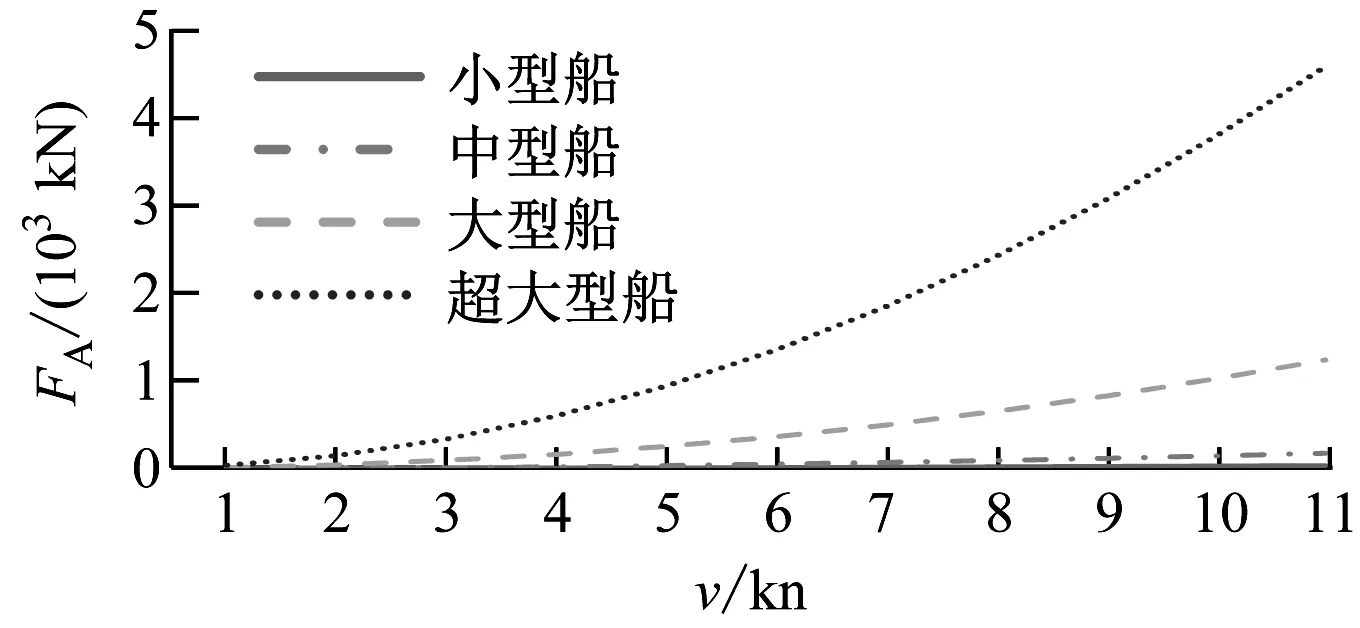
圖3 工況3計算結果(5節錨鏈)
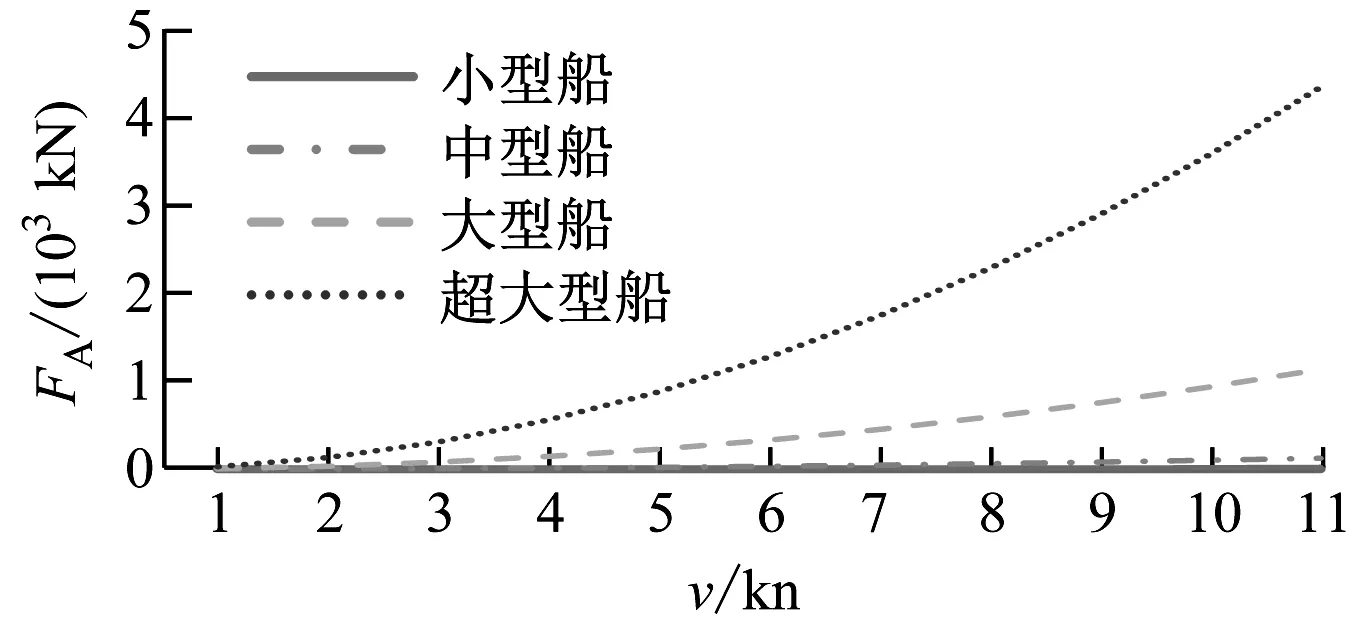
圖4 工況4計算結果(6節錨鏈)
2)拋錨前船舶余速產生的動能主要被船體受到的水流阻力做功抵消,而在錨觸底至抓牢過程中錨鏈張力做功僅為水流阻力做功的0.5%~1.0%。無論是要求不出現拖錨現象(FA≤PA)還是錨機剎車力能控制船舶(FA≤PW),出鏈長度對同一船型錨鏈受力和拋錨航速的影響不明顯,且隨著船舶排水量的增加,影響越不明顯。
3)以下分3種情況討論拋錨航速:
(1)當FA=PA時,計算到的vS為低風險拋錨航速。當拋錨航速以vA不大于vS,即vA≤vS,則FA≤PA,出鏈后即使完全剎住錨機剎車也不會導致拖錨。因此,該拋錨航速適用于對錨位精度要求較高的拋錨作業,但因拋錨航速值較小,拋錨作業耗時較長,增加拋錨前操縱船舶至指定拋錨位置的難度。
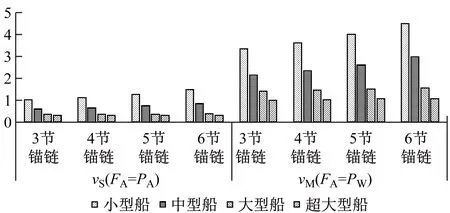
(2)當FA=PW時,計算到的拋錨航速值(vM)為風險可控的拋錨航速,同時也是可拋錨航速的最大值。當vS (3)當vA>vM時,則FA>PW,此時錨鏈受到的張力大于錨機設計的剎車力并遠大于錨抓力,如剎住錨機剎車會導致船舶轉向或拖錨來額外做功抵消船舶的動能,如錨在海底拖動過程中卡住將非常危險,很容易造成錨機剎車損壞、丟錨或斷鏈等事故,嚴重時會導致人員傷亡。vS和vM計算值見表10,其拋錨航速計算結果比較見圖5。 表10 vS和vM計算值 kn 圖5 FA=PA和FA=PW時的拋錨航速計算結果比較 4)因不同拋錨工況對拋錨航速值影響甚小,故采用在4種工況下計算航速的算術平均值作為拋錨航速的控制值,見表11。小型、中型、大型和超大型等4種計算船型對應的低風險拋錨航速值vS分別為1.2 kn、0.7 kn、0.3 kn和0.3 kn;風險可控拋錨航速值vM分別為3.8 kn、2.5 kn、1.4 kn和1.0 kn。 表11 拋錨航速控制值 kn 1)在計算拋錨航速時,忽略了在錨入水到觸底過程中錨受到的水阻力以及錨鏈與錨鏈孔之間的摩擦力。因此,拋錨航速的計算值偏小,偏向于安全。 2)拋錨航速計算值是基于在靜水中不考慮風載荷做功情況下船舶動能定理,因此對地航速和對水航速相等。實際上,錨泊水域的風和流對拋錨航速的計算值會有一定程度的影響,但從良好船藝角度出發,拋錨前艏部一般迎風頂流,因此,進速拋錨時風和流對船舶做功可額外抵消一部分船舶動能,更有利于船舶減速,錨鏈實際受到的張力要小于計算值,因此,拋錨航速計算值偏小,有利于拋錨作業安全。實際控制的拋錨航速約為計算值與流速的和。 3)拋錨航速的計算模型在退速拋錨時確定拋錨航速同樣適用,但相同航速的進速拋錨和退速拋錨時船舶所受到的水流阻力不一致。拋錨前艏向迎風頂流,船舶后退時風和流對船舶做功在一定程度上增加船舶動能,不利于船舶減速,錨鏈實際受到的張力大于計算值,因此,計算到的拋錨航速值偏大,不利于拋錨作業安全。 實際控制的拋錨航速應為計算值減去流速。 4)在拋錨實踐中,在參考拋錨航速計算值的基礎上,船長還應充分考慮到錨泊水域的風、流和浪等自然環境的影響,仔細觀察錨鏈受力情況能盡早發現拖錨,并適時用車控制船舶航速,以保障安全。 文獻[13]建議萬噸級商船拋錨航速控制在2.0 kn以下,滿載1.5 kn以下,超大型船舶0.5 kn以下;文獻[16]提出小型船舶控制在2 kn以內,VLCC控制在0.4 kn以內;文獻[7]和文獻[17]建議萬噸級船舶控制在2 kn以內,VLCC一般控制在0.25~0.50 kn。這些經驗數據對出鏈長度和拋錨過程中是否允許出現拖錨現象都未做出界定。對錨位精度要求較高的定點拋錨作業而言,要求不出現拖錨現象時,選擇計算的小型船、中型船、大型船和超大型船滿載拋錨航速計算值分別為1.2 kn、0.7 kn、0.3 kn和0.3 kn以內;如允許拖錨減速但不至于損壞錨機剎車,則拋錨航速計算值分別為3.8 kn、2.5 kn、1.4 kn和1.0 kn以內。對于中小型船舶在不出現拖錨現象時的拋錨航速計算值小于經驗值,超大型船舶計算值與經驗值基本吻合。 在留有安全余量的基礎上,建議選擇計算的小型、中型、大型和超大型船舶滿載拋錨航速分別控制為: 1)對錨位精度要求比較高的拋錨作業,要求不出現拖錨現象,則拋錨航速需控制在 1.0 kn、0.5 kn、0.3 kn和0.3 kn以內。 2)對拖錨協助減速的拋錨作業,要求拖錨過程中不至于損壞錨機剎車,則拋錨航速控制在3.0 kn、2.0 kn、1.4 kn和1.0 kn以內。 3)為確保錨和錨設備的安全,建議大型和超大型船舶不采用拖錨減速的方式進行拋錨作業。 4)中小型船舶如采用拖錨減速的方式進行錨泊作業除控制好拋錨航速之外,還應控制好拖錨鏈長,一般不應超過1.5倍水深,否則錨鏈與海底的摩擦力將對錨鏈張力的變化產生不可忽略的影響。 本文建立拋錨航速與錨鏈受力關系的數學模型,對小型集散兩用船、中型散貨船、大型散貨船和VLCC等4種實船船型滿載情況下進行計算,對計算值進行分析,并與經驗值進行比較,提出拋錨航速的相關建議。建立的數學模型和計算值可為航海實踐中同類型船舶錨泊作業控制航速提供有價值的參考。該模型可應用于其他船型,能在一定程度上提高船舶拋錨作業的安全性,后期還應對更多不同類型船舶的拋錨航速進行深入的研究,并結合實測數據對建立的模型進行適當修正。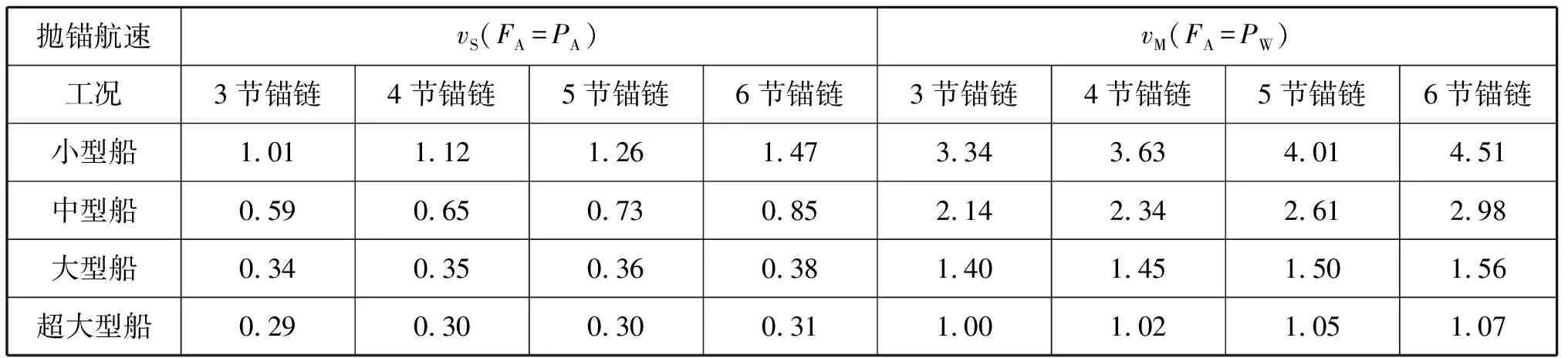

5 計算值局限性分析
6 計算值與經驗值比較分析
7 結束語

