船舶模型在波浪下的崩潰數值仿真及試驗

劉維勤, 黃 宇, 王緒明, 宋學敏

(武漢理工大學 a.交通學院； b.教育部高性能船舶技術重點實驗室；c.國家水運安全工程技術研究中心， 武漢 430063)

船舶在海洋中航行時會遭遇大波浪，從而導致船舶結構發生斷裂，引發海損事故，造成大量的財產損失和人員傷亡。海上大波浪是真實存在的，HAYER等[1]在北海的Draupner海洋平臺上監測到了極端波的存在，監測數據表明，極端波的波高可達25.63 m。KHARIF等[2]列舉了1969—1994年全球因極端波導致的22起船舶事故，導致525人傷亡。MüLLER等[3]記錄挪威籍油船“威爾斯特號”在南非海域被一個極端波嚴重毀壞，艏部嚴重破損，舯部結構嚴重斷裂。

船舶結構遭遇大波浪時的動態強度問題已引起國內外諸多學者的注意。LIU等[4]采用一個非線性的切片理論程序計算集裝箱船在極端波中的波浪載荷，并將波浪載荷載入到非線性動態有限元模型中，結合靜態非線性有限元計算出動態的垂向彎矩(Nertical Bending Moment, VBM)和舯部的轉角。PEI等[5]提出一個結合波浪載荷與理想單元法的極限強度評估系統，可得到舯部的結構崩潰響應。PEI等[6]采用奇點分布和理想單元法分析雙層底散貨船在隔艙裝載工況下的船體強度。目前，這些數值計算方法的有效性還沒有經過試驗驗證。LIU等[7]進行了單波下的屈曲鉸船模試驗，研究極端單波下的船體結構崩潰響應和舯部的大變形，但缺乏相應的數值計算。XU等[8]設計了一個水彈塑性模型試驗，將塑性鉸連接2個船體，得到波浪的遭遇彎矩與極限強度的關系，但在試驗中并未考慮波擊或砰擊產生的振動影響。

目前，研究波浪下船體結構的非線性強度的可行數值計算方法是將波浪載荷與船體強度分開計算，計算時調用波浪載荷求解器和非線性有限元2個求解器，忽略慣性力和動態效應對船體結構強度的影響。本文提出結合三維勢流理論波浪載荷求解器AQWA和非線性動態有限元法求解器MECHANICAL研究船舶結構在波浪下的非線性動態強度。先采用AQWA計算作用在船體濕表面上的水動壓力、船舶運動和慣性力，再將濕表面上的水動壓力和船體運動引起的慣性力施加到結構有限元模型上，最后采用MECHANICAL求解船體結構的非線性動態強度。為驗證該數值仿真方法的準確性和可靠性，設計一個能在試驗水池條件下產生崩潰響應的船體模型，并在水池波浪下對該模型進行崩潰試驗，經過模型試驗驗證的數值仿真方法可用于評估船體結構的非線性動態強度。

1 船體結構的水彈塑性試驗設計

1.1 水彈塑性試驗模型設計

模型試驗是研究波浪載荷作用下船體結構崩潰響應的可行方法。

1)實船結構的崩潰需遭遇真實的海洋極端波，極端波的出現為小概率事件，具有隨機性、瞬時性和不可預測性。

2)由于水池所造波浪的波高過小，普通縮尺比的試驗模型擁有較大的剛度，難以在水池波浪下產生結構崩潰響應，因此，需設計一個特殊的船體模型研究船體結構在波浪作用下的崩潰行為。

船舶在波浪中航行時，舯部遭受的波浪彎矩最大，最有可能發生崩潰破壞。因此，崩潰試驗模型設計為強-弱-強的改良形式。本文的船舶模型與文獻[7]采用的模型相似，見圖1和圖2，試驗模型由舯部區域用鋁合金制造的屈曲鉸構件和左右兩端由玻璃鋼制造的船體分段組成，左右兩端由玻璃鋼制造的船體分段的剛度很大，試驗中不會產生任何變形，可視為剛體。舯部采用鋁合金材料(楊氏模量E=69 GPa, 泊松比ν=0.3, 屈服強度σY=120 MPa)制造的屈曲鉸構件剛度較小，在水池波浪下能產生結構崩潰響應。該屈曲鉸構件不完全釋放左右剛性船體的轉動，可實現對船體梁結構彈塑性特征的模擬，試驗時可通過測量左右兩端剛性船體分段的轉角變化反映舯部屈曲鉸構件的大變形響應。

圖1 屈曲鉸構件

圖2 試驗模型

屈曲鉸構件如圖1所示，其縱向長度為100 mm，兩端是直徑為100 mm、厚度為10 mm的鋁盤，2個鋁盤由上下2個具有一定厚度的鋁片相連，其中上鋁片要比下鋁片窄且薄，符合船舶上部結構要比下部結構更容易破壞的結構特點。屈曲鉸左右兩端的鋁盤上設計4個螺絲孔，螺栓通過這些螺絲孔將舯部的屈曲鉸構件與左右2部分剛性船體分段緊固連接，形成完整的水彈塑性試驗模型。

2個船體分段為方駁狀的理想形狀，分別稱為船體分段1和船體分段2，2個船體分段除了通過舯部的屈曲鉸連接以外，還向舯部延伸的重疊區域分別設置了開孔，利用直徑略小于開孔的螺栓串接船體分段1和船體分段2，從而在舯部形成理想的鉸接方式，以消除屈曲鉸的擠壓和剪切變形，僅保留彎曲變形。每個船體分段有3個隔艙，每個隔艙的空間用來放置傳感器和壓載。試驗模型的主尺度見表1。

表1 試驗模型的主尺度 m

通過測試2個船體分段之間的轉角變形反映船舶模型在波浪下的大變形響應。為獲得動態的轉角變形，在2個船體分段的中間隔艙內放置無線動態傾角儀，分別命名為1號無線傾角儀和2號無線傾角儀，見圖3。該無線傾角儀由德國制造，量程為±30°，測量精度為0.025°。采用無線接收器接收無線傾角儀發出的信號，并將其傳輸到電腦端進行試驗數據記錄，1號傾角儀記錄的數據記為θ1，2號傾角儀記錄的數據記為θ2，2臺無線傾角儀記錄的數據之差θb為試驗模型的轉角變形，即

θb=θ1-θ2

(1)

圖3 測試儀器布置剖視圖

1.2 波浪模型和試驗工況設計

試驗在武漢理工大學交通學院流體實驗室玻璃水槽內進行(見圖4)，該波浪水槽裝備的造波機可造出滿足本文要求的規則波浪。SHI等[9]和LIU等[10]的研究結果表明:當波高相同，波長接近或等于1倍船長時，舯部會產生最大的變形和彎矩，本文波長取1倍模型長度，通過改變波高定義不同的試驗工況，模型試驗工況見表2。

圖4 波浪玻璃水槽

表2 模型試驗工況

塑形累積影響結構的載荷位移關系，為排除塑形累積的影響，本文僅研究造波穩定后第一個規則波周期內船體結構的崩潰響應。試驗中在艏部布置1臺波高儀，可獲得波面升高的時程曲線，工況2、工況4和工況7的波面時程曲線見圖5。

1.3 屈曲鉸的極限強度試驗及數值仿真計算

在開展水彈塑性試驗之前，先了解屈曲鉸構件的極限承載能力。通過4點彎曲試驗和非線性有限元方法獲取屈曲鉸構件的極限承載能力和載荷位移曲線。屈曲鉸構件的4點彎曲試驗示意見圖6，屈曲鉸和兩端的剛性延伸段通過螺栓固定在一起，支撐屈曲鉸的圓撐穿過延伸段靠近中部的圓孔，以保證屈曲鉸和延伸段可繞圓撐轉動。通過在延伸段左右兩端的托盤上增加質量塊，向屈曲鉸施加垂向彎矩載荷；試驗時采用百分表和拉力傳感器分別記錄垂向位移和拉力值，通過簡單的數學變換便可得到屈曲鉸的極限彎矩和載荷位移曲線。屈曲鉸的極限強度數值計算在ABAQUS中進行。屈曲鉸構件的轉角-垂向彎矩曲線見圖7，試驗和數值仿真時屈曲鉸構件的失效模式見圖8。

圖5 工況2、工況4和工況7的波面時程曲線

圖6 屈曲鉸構件的4點彎曲試驗示意

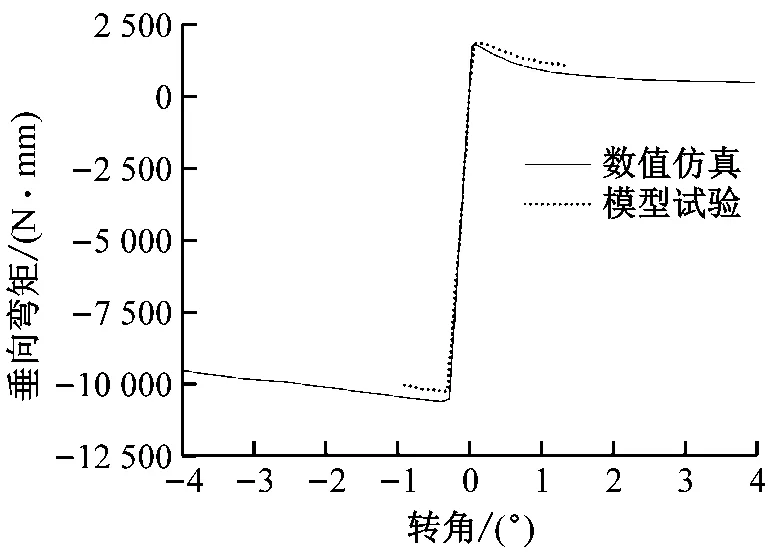
圖7 屈曲鉸構件的轉角彎矩曲線

圖8 屈曲鉸失效模式

屈曲鉸構件4點彎曲試驗和數值仿真計算的極限承載能力見表3。由表3可知：屈曲鉸的極限彎矩試驗值與非線性有限元計算值相差不大，利用數值方法計算屈曲鉸構件的極限強度是可行的。

表3 屈曲鉸極限強度點的極限彎矩和轉角

2 船體結構非線性動態強度數值仿真

本文提出一種結合三維勢流理論和非線性動態有限元的數值仿真方法研究船體結構在波浪作用下的非線性動態強度，數值仿真計算在ANSYS中進行，需調用AQWA和MECHANICAL進行求解計算。數值仿真分析思路見圖9。

圖9 數值仿真分析思路

1)建立數值計算模型。根據模型試驗的詳細尺寸數據建立水動力模型和船體有限元模型。水動力網格模型見圖10，包含5 894個單元。結構網格模型見圖11，與模型試驗一致，由左、中、右3部分組成，考慮數值計算精度，對屈曲鉸部分進行網格細化，屈曲鉸部分包含10 184個單元，整個結構網格模型共包含30 750個單元。

圖10 水動力網格模型

圖11 結構網格模型

2)結構預計算。在MECHANICAL中進行靜態結構預計算，提取結構有限元模型的轉動慣量和重心高度等信息。

3)波浪載荷求解。提取結構預計算的轉動慣量和重心高度等信息并將其輸入AQWA中。

4)結構非線性動態強度計算。先在動態強度求解器中設置系列約束，實現對模型試驗中各種約束的模擬；在左、右2個剛性部分的底部施加彈簧約束，模擬重力和靜水力的耦合效應；在左、右2個剛性部分和屈曲鉸部分之間施加設置綁定約束實現對螺栓固定的模擬；在舯部左、右個剛性部分重疊處設置鉸接約束，實現對鉸接約束的模擬。隨后將步驟3)求解的波浪載荷傳遞到結構網格模型中，對波浪載荷作用下的非線性動態強度進行求解。

3 模型試驗及數值仿真結果分析

3.1 船體舯部的時域轉角變形對比分析

試驗開始之前，分別在試驗模型兩端的隔艙中布置1臺無線傾角儀，記錄試驗模型的2個船體分段在規則波下的縱向傾角運動，2個船體分段之間的傾角運動之差便是試驗船體結構舯部屈曲鉸的轉角變形。通過模型試驗和數值仿真計算獲得不同波高下屈曲鉸的動態轉角變形，規則波的波浪載荷輸入頻率在低頻范圍內，因此由波浪載荷引起的船體遭遇變形是一種低頻響應。對由試驗測量直接得到的舯部動態轉角變形進行低通濾波，可得到波浪載荷導致的低頻船中遭遇變形，過濾掉高頻顫振部分，這與數值仿真計算相符。工況1、工況2、工況4、工況5、工況7和工況8下的舯部時域轉角變化曲線見圖12。

a)工況1時域轉角曲線b)工況2時域轉角曲線

c)工況4時域轉角曲線d)工況5時域轉角曲線

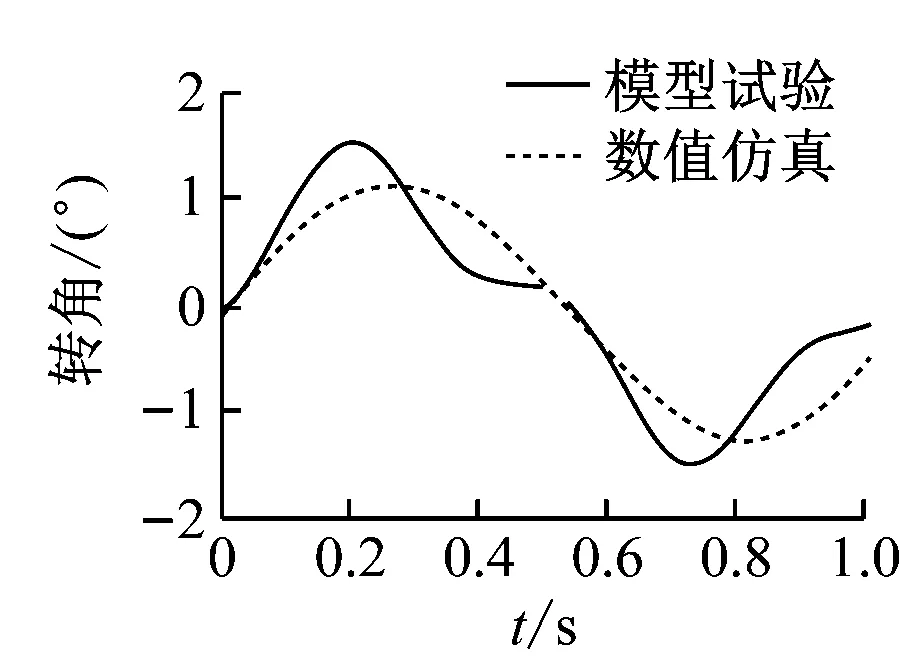
e)工況7時域轉角曲線f)工況8時域轉角曲線

由圖12a和圖12b可知：工況1和工況2下中垂時最大的舯部轉角Rs大于極限強度對應的轉角θs，中拱時最大舯部轉角Rh小于極限強度對應的轉角θh，表明船體結構在中垂時已進入極限強度，而在中拱時處于彈塑性變形階段，還未進入極限強度。由圖12c和圖12d可知：中垂和中拱時最大轉角變形R已接近甚至超過極限強度對應的轉角θ，這表明在這2個波高下，船體結構不論是遭遇中垂變形，還是中拱變形，都已接近甚至進入極限強度階段。由圖12e和圖12f可知：中垂和中拱時最大轉角變形R已大大超過極限強度對應的轉角θ，這表明在此波高下船體結構已產生塑性大變形。由圖12a～圖12f可知：舯部時域轉角變形并不是嚴格按照圖5所示波面升高的形式變化的，不僅船體結構的中垂和中拱強度不同，而且在試驗和數值計算中產生舯部大變形，是由船體結構產生崩潰變形導致的。工況7中船體處于中拱時的運動和變形對比見圖13。

a)水動力數值模型

b)船體崩潰試驗模型

c)非線性有限元模型

3.2 舯部的時域非線性彎矩對比分析

船體結構在波浪載荷作用下達到極限強度，此時有必要研究舯垂向彎矩，了解船體結構的承載能力的變化。屈曲鉸的載荷位移曲線反映屈曲鉸的非線性彎矩與轉角之間的關系，第1.3節通過屈曲鉸的4點彎曲試驗驗證采用非線性有限元法計算屈曲鉸極限強度的可靠性，得到屈曲鉸的載荷位移曲線，并通過模型崩潰試驗得到舯部時域轉角曲線。因此，通過屈曲鉸的載荷位移曲線舯部的時域轉角曲線進行轉化，可得到船體結構的時域垂向彎矩曲線工況1、工況2、工況4、工況5、工況7和工況8下的舯部時域垂向彎矩變化曲線見圖14。

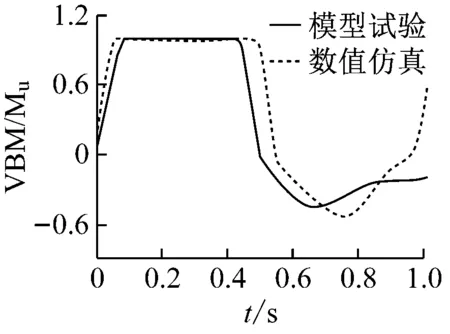
a)工況1時域VBM曲線b)工況2時域VBM曲線

c)工況4時域VBM曲線d)工況5時域VBM曲線

e)工況7時域VBM曲線f)工況8時域VBM曲線

利用最大垂向彎矩與極限彎矩的比值VBM/Mu評估船體結構是否還能繼續承受外載荷。若VBM/Mu<1，表明船體結構還未達到極限強度狀態，船體結構還具有一定的承載能力，VBM/Mu的值越小，說明船體結構的富余強度越足，可繼續承受的外載荷越大；若VBM/Mu的值接近甚至等于1，表明船體結構達到極限承載狀態，增大外載荷會導致船體結構崩潰，承載能力下降。由圖14a和圖14b可知：中垂狀態下的最大垂向彎矩與中垂極限彎矩的比值VBM/Mu接近于1，而中拱狀態下的最大垂向彎矩與中拱極限彎矩的比值約為0.6，表明船體在中拱受力狀態下還有一定的承載能力，而在中垂狀態下已接近其所能承載的最大外載荷。圖14c和圖14f可知：VBM/Mu的值已接近甚至等于1，無論是處于中垂狀態，還是處于中拱狀態，都已達到船體結構的極限承載狀態。

3.3 改變波高對船體結構強度的影響

隨著規則波的波高增加，對所有工況下的舯部最大轉角變形和中拱狀態下VBM/Mu的值進行綜合分析。舯部最大轉角隨著波高增加的變化曲線見圖15，中拱時VBM/Mu最大值隨著波高增加的變化曲線見圖16。由圖15和圖16可知：船體結構的遭遇轉角變形和垂向彎矩隨著波高的增加呈非線性增加，表明波高對波浪載荷和遭遇變形有顯著的影響。

圖15 腫部最大轉角隨波高的變化曲線

圖16 中拱時VBM/Mu最大值隨波高的變化曲線

4 結束語

本文提出一種結合三維勢流理論和非線性動態有限元的數值仿真方法，研究船體模型結構在波浪作用下的非線性動態強度，同時，設計并開展一個水池波浪下的船體結構模型崩潰試驗，試驗結果用來修正和改進提出的數值仿真方法。通過對船體結構的模型崩潰試驗結果和數值仿真結果進行分析，得到以下結論：

1)該模型試驗方案能產生水池波浪下的結構崩潰響應。

2)數值仿真結果與試驗結果吻合度較好，表明提出的數值仿真方法可用于評估船體結構在波浪下的非線性動態強度。

3)舯部轉角變形隨著波高的增加呈現出非線性增長的趨勢，船體結構在大波高條件下進入結構非線性，甚至達到極限強度的狀態，說明本文設計的船體結構模型崩潰試驗模型可在水池波浪條件下發生崩潰。

今后可將該數值仿真方法用于工程化應用，評估實船結構在波浪作用下的非線性動態強度。