數學情境問題解決錯誤分析與評價

鄧海英，嚴 卿，魏亞楠

數學情境問題解決錯誤分析與評價

鄧海英1，嚴 卿2，魏亞楠3

（1．湖南第一師范學院 數學與計算科學學院，湖南 長沙 410205；2．湖北大學 數學與統計學學院，湖北 武漢 430062；3．南京師范大學 數學科學學院，江蘇 南京 210046）

在問題解決中，出現錯誤是不可避免的，錯誤的合理性正逐漸得到教育工作者的認可，將其看作一種有效的教學資源．情境問題解決與核心素養密切相關，因此，從核心素養的視角出發，構建數學情境問題解決錯誤分析框架，分析結果如下：（1）在6個數學核心素養成分中，數學抽象、邏輯推理錯誤出現得最多；（2）數學核心素養三級水平中，被試普遍難以達到二級水平．研究亦得，不理解情境是影響錯誤的核心因素．教師在教學中應深化學生對情境的理解和培養情境中的知識遷移能力，以促成數學核心素養的培養．

數學情境問題解決；錯誤分析與評價；數學核心素養；情境

1 問題提出

中國最新頒布的《普通高中數學課程標準（2017年版）》給出了數學核心素養六大成分的具體內涵，并相應劃分了三級水平，為數學核心素養培養的水平提供了理論依據和判斷標準．大型國際教育測量項目PISA秉持弗賴登塔爾的現實數學教育觀（RME），在開發測試體系的時候便提出了“素養”的概念（“不管是哪個國家或地區，不管學生在學校學習的內容是什么，學習的目標應該是培養學生應用知識的能力，使學生能夠在實際生活中應用所學知識，進而解決問題”），試題也都基于現實情境，通過學生在不同現實情境下解決實際問題的表現來評價他們的素養[1-2]．PISA測試中有關情境的研究，比較早期的有Chipman等人發現對情境的熟悉度對應用題的表現有很小的正面影響[3]；也有個別研究宣稱并不能確定“情境熟悉度”和“正確率”之間的關系是什么[4]；還有從男女性別對情境的不同熟悉度和興趣對PISA的影響進行的研究，但是這方面的研究還不完善[5]．這些研究主要針對15歲學生（在世界各國大部分已經完成義務教育階段），小學階段情形如何還不能確定．

當前核心素養是中國新一輪深化課程改革的主要方向，然而不少一線小學數學教師對核心素養怎么進課堂感到迷茫，不知如何落實．這里不妨借鑒PISA測試的有益經驗，將在現實情境中解決問題的能力作為核心素養重要的參考指標，已有國內外學者關注到了現實情境與數學核心素養的關系，認為數學核心素養要借助特定的情境潛移默化方能習得[6]，“讓知識學習與多樣化的情境相聯系，讓學生置身真實問題情境、親歷復雜的問題解決過程，可以促進核心素養的培養與發展”[7]．因此，基于PISA和數學核心素養的共同理念，改編PISA試題，選擇小學四年級學生（三~四年級是抽象[8]、歸納和演繹能力發展的關鍵時期[8]．這3種能力是數學核心素養的關鍵成分）為研究對象，測試在情境中解決數學問題的能力，分析在情境中的錯誤以及錯誤原因．分析學生的錯誤是最重要的、也是最困難的[9]，但依然試著努力去做，希望減少數學錯誤的發生，為培養核心素養提供有用的教學資源和參考．

2 測試卷的水平劃分和指標分析

2.1 測試卷的水平劃分

喻平教授認為要發展學生的數學核心素養，就要發展學生的學科關鍵能力[10]，學科關鍵能力生成的本源是知識，生成機制是知識理解、知識遷移、知識創新3種知識學習形態，對應生成的結果是學科關鍵能力的一、二、三級水平[11]．由此，從知識與能力的角度提出評價數學核心素養的框架，即3種知識學習形態對應著學科關鍵能力的三級水平[12]．情境問題解決也是一種數學能力，知識也是其生成的本源，需要理解、運用知識，甚至帶有創造性．所以，測試卷借鑒該框架，將數學情境問題解決水平分成知識理解、知識遷移、知識創新3個等級．

測試卷由數學教育專業教授、研究生和小學數學特級教師根據PISA測試題共同改編完成，參照PISA2012的情境分類，將情境分為個人情境、公共情境、科學情境、教育與職業情境．個人情境聚焦個人日常生活的各個方面；公共情境聚焦公民、地方、國家或全球；科學情境要求學生運用數學知識解決和科學技術相關的問題[5]；教育與職業的情境指與學生的學校生活或工作環境相關的情境[13]．測試共9道大題13個小題，分別簡稱為登富士山、跑道賽跑、最大心跳率、建筑距離、顏色合成、公園排隊、雇傭關系、花圃面積、開車上班．試卷各題項的測試內容、三級水平劃分以及情境類型見表1．要特別提出的是，由于情境的復雜性，這些對應不是絕對的，只是給出各題項最相關的情境類型．

2.2 測試卷的指標分析

PISA試題難度要求必須是中等的，所以PISA測試中不會包含難度非常大或者難度非常小的題目．測試題全部由PISA試題改編而來，有必要對試卷難度進行分析，用SPSS 17.0進行分析如表2．

表1 數學情境問題解決試卷各題項水平劃分與情境類型

表2 測試卷題項得分與總分的相關系數及試卷難度

表2結果顯示，總測試難度系數為0.474，接近中等難度臨界值0.4，與PISA難度接近，但存在個別難度較大和較小的題，如題9和題2，但還是在可接受范圍之內．（另注：測試卷的3個水平是關鍵能力的水平劃分，并非難度水平劃分．雖然二者確實從理論上存在一致性，但并非絕對的．如題4屬于知識理解水平，但是理解層次加深，使得難度大于知識遷移水平的題5、6(1)、7(1)(2)；又如題7(3)屬于知識遷移水平，情境遷移與(1)(2)小題類似，但是運算方法要復雜一些，使得難度大于知識創新水平的題8．）表2結果還顯示所有題項與總測驗得分都在0.001的顯著水平上相關，每個題項與總分的相關系數在0.239~0.729之間，說明題項與測試卷的測驗目標一致，因此保留所有題項．

結果顯示三級水平之間的內部一致性系數在0.555~ 0.725之間，總測試的內部一致性系數為0.799，說明該測試卷的總體信度較好．三級水平之間的相關系數小于每個水平與總測試的相關系數，表明該測試卷具有較好的結構效度．同時，一級水平和三級水平之間的相關系數小于一級水平與二級水平，同時也小于二級水平與三級水平，說明3個水平的等級劃分是合理的．

由以上分析得到，此次測試卷難度、信度、結構效度等各項指標都較好，為下文分析、評價錯誤提供了合理的前提．

3 數學情境問題解決錯誤分析框架

對數學核心素養各成分三級水平的描述[14]進行歸納，作為數學情境問題解決錯誤的分析框架見表4．通過這種框架的建立，旨在發現數學情境問題解決典型錯誤的水平分布．

表3 測試卷題項克倫巴赫a系數和結構效度

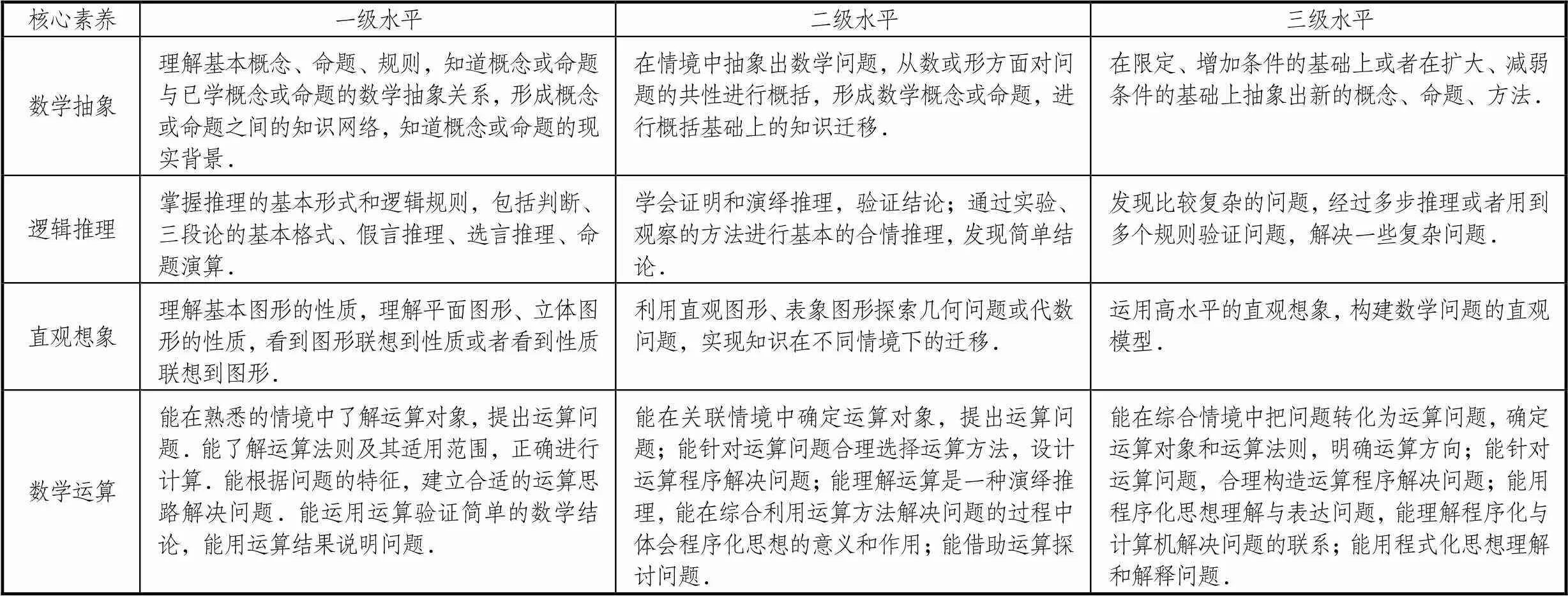
表4 數學核心素養的三級水平劃分與內涵

表4（續） 數學核心素養的三級水平劃分與內涵

4 數學情境問題解決典型錯誤分析

4.1 題項錯誤率統計

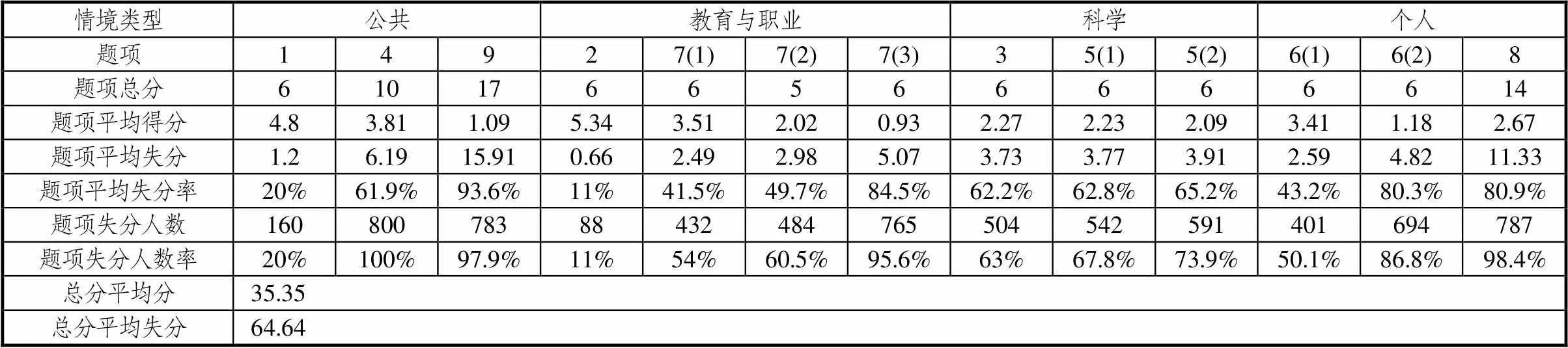
表5 數學情境問題解決測試失分統計

表5數據說明出錯的人次很多，題目錯誤率也很高，每道題都有人做錯，4種情境出錯的程度不一．以下給出如圖1所示4種情境出錯人數率的散點圖（橫軸1~13為13個小題題號，縱軸0~100為省去百分號的出錯人數率）．

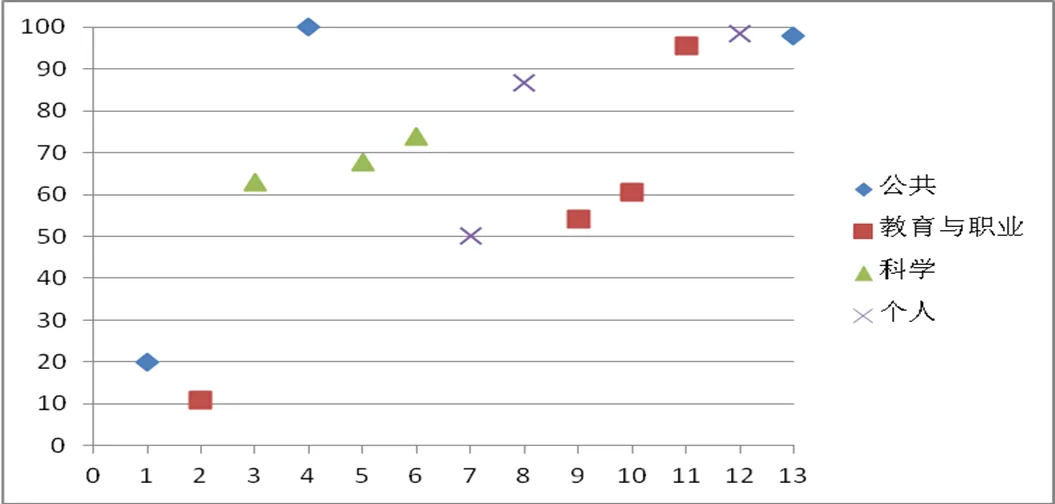
圖1 4種情境出錯人數率

從圖1可看出，此次測試人數出錯率內部相對最穩定的是科學情境，其次是個人情境，波動最大的是公共情境，其次是教育與職業情境，13個小題的出錯人數率均值67.62%，方差0.085，總體上看，出錯人數率隨題號往后有一定的上升趨勢．

4.2 題項錯誤分析

題1：登富士山．

此題除去沒有作答，錯誤結果還有280?000、270?000、210?000、27?000、1萬、8?971、9?000、4?500、4?000、3?400、3?000、2?700、2?100、1?000、999、900、700、540、500、430、360、388、344、321、320、310、270、261、200、114、100、94、56、51.83、38、35、31、30、6、4.93、3等．除了可能因為粗心產生的計算錯誤或者題意弄錯之外，反映了典型錯誤：被試對登富士山的情境不熟悉，因而不能將情境中的總天數、總人數正確轉化為求平均數的條件．甚至還出現了人數為小數的情況．這類典型錯誤指向數學抽象一級水平不足，同時還缺乏基本的邏輯推理能力．

題2：跑道賽跑．

該題除了沒有作答和填了時間“9.87”之外，還出現了一些非常“奇特”的答案：出現了15次“1”，3次“2”，4次“4”和1次“5”（這些被試在不同學校或同校不同班，答案純屬巧合）．典型錯誤：被試可能不熟悉跑道賽跑的情境，不知道時間與排名的關系，而是錯誤地運用了個人經驗，比如認為位于跑道1或5的選手占據了跑道優勢，所以跑起來更快．這類典型錯誤指向邏輯推理一級水平不足，而填了“2”或“4”的被試有可能是因為3與2和4相鄰，所以粗心誤填，觀察能力不夠強．

題3：最大心跳率．

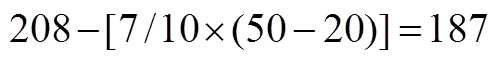
題4：建筑距離．

該題錯誤答案分成4類：給出了最大值和最小值、給出最大值或最小值、無作答和作答全錯．典型錯誤：被試對三點距離知識和3個建筑的“位置情境”都缺乏全面的理解，將“兩點共線”錯誤遷移至“三點共線”，錯誤的知識產生錯誤的遷移，沒有建立起直觀的三角模型與建筑實際位置進行對應．這類典型錯誤指向直觀想象的二級水平和數學建模的二級水平不足．對于只給出一個值的被試，其直觀想象不足二級水平，數學建模不足一級水平．沒有作答或邏輯不清的樣本則尚未達到直觀想象和數學建模的一級水平．

題5：顏色合成．

該題是科學情境．從錯誤的答題過程來看，存在典型錯誤：盡管學生可能認識數組，但是不少被試理解不了題中數組的構成（比如數字大小和排列順序）與顏色的關系，不能給出完整答案，或是只能給出數組中的個別數字，并且順序還不一定對，不能完成知識的情境遷移．這類典型錯誤指向數學抽象二級水平、數學建模二級水平、數據分析二級水平和邏輯推理的三級水平等多種水平的不足．

題6：公園排隊．

該題主要錯在沒有作答或者部分知識點正確．典型錯誤：將知識遷移到現實情境中時沒有弄清題目條件和問題之間以及多個條件之間的關系，邏輯不清、缺乏條理，不能實現點分線段到游客排隊情境的遷移，導致不能正確列式，個別被試列式正確但計算錯誤．這類典型錯誤指向數學抽象二、三級水平，邏輯推理三級水平，直觀想象二級水平，數學運算二級水平等多種水平的不足．

題6(2)存在的典型錯誤，除與題6(1)相似的幾種外，還出現了被試沒有列式101-1=100的錯誤，也是沒有在排隊的情境中聯想到“植樹原理”．這類典型錯誤指向數學建模二級水平的不足．

題7：雇傭關系．

題7(1)出錯的被試除了沒有作答，錯誤的理由各異：比如因為小菊工作時間長，干活久，所以選小菊；因為6+5=11<8+4=12，所以選小蘭；雖然小菊種花慢，但是種得好，所以選小菊；還有更多的被試沒有理由，就寫個小菊，等等．典型錯誤：被試對工作效率不理解，不能將效率的意義遷移到雇傭關系情境中，甚至還產生了誤區：工作時間越長，所以做得越多，沒有理解這里是單位時間．題7(2)本質上也是計算工作效率．這兩個題項反映的典型錯誤類似，都是在表格表示的方法下，對工作效率與工作時間、工作總量、單位工作量之間的關系不清楚．這類典型錯誤指向邏輯推理一、二級水平和數據分析一、二級水平的不足．

題7(3)相比起題7(1)、7(2)，比較工作效率的情境要復雜一些．這道題除了因工作效率概念不清、算法出錯和其它各種具有偶發性的錯誤之外，有一類錯誤非常典型，見圖2．

圖2 典型錯誤

圖2中右邊解答思路是對的（但220計算錯誤和作答結論出錯）．這次測試中有11.3%的被試得出了96和80的結果，具體過程舉例如圖3所示．

圖3 解答舉例

這種錯誤的解答在于少乘了兩次10，原因是被試對較復雜情境下的多步乘法理解不透徹．題7(3)的典型錯誤還應包括邏輯推理三級水平和數據分析三級水平的不足．

題8：花圃面積．

該題屬于個人情境，題目已給出代表花圃的平面圖形矩形，幫學生完成了抽象的第一步，只有13個被試給出了3種及以上的分法，有一定的創新能力，少部分被試能給出一到兩種分法，有欠創新．一半的被試沒有作答或者只是在矩形上思路不清地點畫了幾筆，這些學生不明白矩形的用途，沒有將三等分花圃的面積轉化為三等分矩形的面積，情境遷移失敗，更無從談分法創新．典型錯誤：被試將實物轉化成平面圖形的知識遷移水平非常不足和探索幾何問題的創新能力也相當缺乏．這類典型錯誤反映數學抽象的二級水平、直觀想象的二級水平有很大欠缺．

題9：開車上班．

此題中開車時間會因等待紅綠燈的不同而變化，是一個變化的量，但是學生對此不敏感，視紅綠燈等待時間為無用的數據．只有17個被試完成要求，其他很多被試沒有作答，還有不少被試沒有設計情境，只是按照常規思路求出了蔡老師的家到辦公大樓的距離或中間某一段距離等，與題意不符，還有少部分被試“陷”在多步運算中“跳”不出來，思路和計算都不對．典型錯誤：學生對真實的復雜生活情境缺乏經驗，限制在書本的理想情境里，形成思維定式、缺乏創新．此題的典型錯誤指向數學抽象、數學運算和數據分析的三級水平不足．

4.3 典型錯誤水平分布

對上述錯誤水平進行頻數統計，得到錯誤水平分布表如表6所示．

表6 數學情境問題解決錯誤水平分布

從表6可以看出，數學抽象、邏輯推理是典型錯誤出現得最多的兩個數學核心成分，數據分析次之．另外，除了邏輯推理之外，其它5個數學核心素養成分各自三級水平出錯最多的都是二級水平．

5 結論

國際上對影響學生PISA成績的因素做了一些宏觀的分析：社會階層[15]、教育公平和學校環境等[16]，這些因素也可能是學生在PISA測試中出錯的間接原因；學生的粗心、觀察能力不強、策略[17]不足等，也是錯誤產生的重要原因，在此次測試中普遍存在．此外，學生的自我效能感、焦慮等[18]也是學生出錯的心理等原因．下文根據題項錯誤分析，從情境的角度總結錯誤原因．

（1）情境類型之間沒有難易之分．

通過上文4種情境錯誤人數率散點圖可以看到，每個情境類型中都有不同層次的人數出錯率，4種情境類型之間沒有難易的區別，不能肯定學生會在哪個情境中更容易產生錯誤．

（2）不熟悉情境加重認知負荷．

（3）不理解情境影響遷移和創新．

熟悉情境并不一定就理解情境，不熟悉的情境在知識的充分理解下也能理解情境．因此，理解情境是解決問題的關鍵，對情境的理解是遷移和創新最基本的前提．如學生理解不了題5的科學情境，同時也失去了數組知識遷移的方向和目標．又如題9要求學生根據條件“創設情境”，這本身就置學生于一種“動態”的問題解決情境之中，但是學生對由題目條件而生可又不是“現成”的“情境”不理解，因此不能創新．

（4）對情境不感興趣影響正確率．

測試之余，對學生進行了問卷調查，其中有如下問題“你覺得剛才做的測試卷題目很有意思嗎”“你對有故事情節的數學題目很感興趣嗎”涉及到學生對題目的興趣，其實質也是學生對試題情境設計的興趣．問卷結果顯示，學生對試題情境的興趣與測試成績呈現弱相關性．學生對情境的興趣會影響他們解題動機和毅力等，正面的作用會激勵學生，負面的作用則會讓學生變得消極，比如放棄作答或者敷衍了事，從而增加錯誤．

Chipman等人指出學生對情境不感興趣的情況最容易發生在學生不熟悉情境的時候[3]．用圖4表示情境類型、熟悉、理解、興趣四因素之間的關聯：對情境的理解占據中心地位，同時受情境類型、熟悉度的制約；類型和熟悉度影響興趣，但是對情境很好的理解又可以改善對情境不熟悉和不感興趣的狀況．因此，不理解情境是學生出錯的首要原因．

6 啟示與建議

（1）創設多樣化的情境，深化理解．

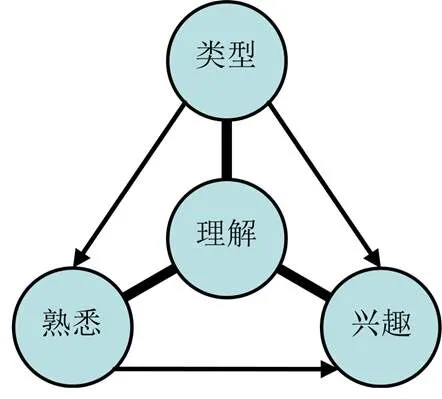
圖4 四因素關聯圖

教師在教學中要創設多樣化的、合理的情境，并要深化理解，而不只是為了“裝飾”停留在表面．如何深刻理解情境？能夠判別情境傾向哪個類型、是純數學的還是現實的，這是最基本的要求，更重要的是要理解這個情境用到什么知識、解決什么問題，主要方法是什么？歸根結底，首先還是要加強對知識的理解，除了“4個基本理解”（知識的基本性質、基本事實和結論、基本概念和規則以及基本方法），還包括了解知識的源頭、形成概念和命題體系、理解規則和法則的結構以及使用條件等3個較高的要求．只有深層次的理解，抽象出知識的本質屬性，才能實現在情境中的靈活運用．典型例子如題4，所有被試都沒有深刻理解在不同條件下的求距離的方法，存在“知識盲點”而造成了普遍的錯誤．

（2）提高情境中的知識遷移能力，發展數學核心素養．

表6顯示，數學核心素養各成分的二級水平出錯最多，學生也就達不到相應的三級水平．表4也顯示，數學核心素養各成分的二級水平較普遍地涉及到了知識遷移．這為培養數學核心素養提供了一條思路：提高情境中的知識遷移能力即能促進數學核心素養的發展．表4中二級水平的內涵從知識的角度概括了在情境中遷移的目標，在教學中可結合具體教學內容進行實踐，促成目標的達成．如題7，在教學中應讓學生理解“工作效率”的實質，掌握總工作量、總工作時間和單位工作量這3個要素之間的相互轉化關系和等價作用，再實現在不同情境中的遷移．

（3）重視數據分析能力的培養，與時俱進．

當今社會，數據已經滲透到各個行業．從情境的角度看，數據的主要來源是客觀現實世界，任何數據不僅僅是包含數量、文字、符號、圖形等抽象信息，必然還包含了與現實情境有關的背景信息，這些背景信息中的人或事物就構成了數據的情境[20]．如題9，“每個紅綠燈的等待時間2分鐘”是一個非常關鍵的條件，既是數學的信息，也是情境的信息，是一個典型的“情境數據”，但是學生幾乎都忽視了．教師對這樣的問題應該多分析情境中的數學信息，善于抓住“情境數據”，幫助學生改變對“數據”的狹隘理解．此外，要培養學生的數據分析能力，必然要發展學生的閱讀能力，不但是要能看“文字”，還要能讀懂題中的數量、符號、圖象等一切能夠承載事物信息的載體．當然，發展學生的數據分析能力不能急于求成，教師應按部就班，提供現實情境中的典型案例，讓學生隨著學齡的增長，經歷建立數據分析意識—掌握數據分析方法—積累數據分析經驗的學習過程，逐步形成數據分析素養．

（4）加強培養數學抽象和邏輯推理能力依然是根本．

抽象能力和邏輯推理能力是思維品質深刻性的重要指標．通常在教學中，教師可展示數學抽象的情境背景以降低抽象層次，反過來又影響學生在情境中抽象出數學問題的能力，讓學生學會剝離情境中的非本質屬性，逐步實現“去情境化”，最終脫離較低層次的情境支持而發展成獨立的數學知識．邏輯推理的依據是“事實”和“命題”，是建立在情境基礎上的思維過程[20]，現實情境或純數學情境是培養學生邏輯推理能力的有力支撐，可以啟示學生不必犯一些“低級”錯誤，如題1中的登山人數絕對不可能是小數．很多時候，學生邏輯推理素養的形成，在本質上不是靠教師“教”出來的，而是靠學生自己“悟”出來的[21]，合適的情境就是一個“悟”的好環境．

數學情境問題解決需要學生多種核心素養在情境中共同作用，是一種較高水平的數學素養．測試結果顯示四年級學生在六大核心素養上水平欠缺，對教師而言，明確數學核心素養的內涵、各成分三級水平的劃分，了解國際先進教育思想，形成科學的知識觀、數學觀，是培養學生數學核心素養的必備素質；在數學教學中合理對待學生的錯誤，化“錯誤”為資源，以“錯誤”促教學，是正確的教學態度；了解情境與核心素養的密切關系，發揮情境在培養數學核心素養中的作用則是有效的教學策略．

[1] 陳敏，楊玉東．小學生解決真實情境問題的調查研究——基于PISA數學素養的視角[J]．上海教育科研，2016（9）：46–49，54．

[2] OECD. What is PISA [EB/OL]. (2018–02–06) [2019–07–09]. http://www.oecd.org/pisa/aboutpisa/.pdf.

[3] CHIPMAN S, MARSHALL S, SCOTT P. Content effects on word problem performance: A possible source of test bias [J]. American Educational Research Journal, 1991, 28 (4): 897–915.

[4] DE LANGE J. Large-scale assessment and mathematics education [M] // LESTER F K. Second handbook of research on mathematics teaching and learning. Charlotte: Information Age Publishing, 2007: 1?112–1?142.

[5] STACEY K，TURNER R．數學素養的測評——走進PISA測試[M]．雷一鳴，譯．北京：教育科學出版社，2017：30．

[6] LENGNIK K. Reflecting mathematics: An approach to achieve mathematical literacy [J]. ZDM the International Journal on Mathematics Education, 2005, 37 (3): 246–249.

[7] 張華．論核心素養的內涵[J]．全球教育展望，2016，45（4）：1–15．

[8] 林崇德．智力發展與數學學習[M]．北京：中國輕工業出版社，2011：185．

[9] 郜舒竹，劉瑩．兒童數學學習中思維的自然結構及其正誤辨別[J]．課程·教材·教法，2010，30（7）：42–45，76．

[10] 喻平．發展學生學科核心素養的教學目標與策略[J]．課程·教材·教法，2017，37（1）：48–53，68．

[11] 喻平．學科關鍵能力的生成與評價[J]．教育學報，2018，14（2）：34–40．

[12] 喻平．數學核心素養評價的一個框架[J]．數學教育學報，2017，26（2）：19–23，59．

[13] 陳慧，袁珠．PISA：一個國際性的學生評價項目[J]．外國中小學教育，2008（8）：53–58．

[14] 喻平．數學核心素養的培養：知識分類視角[J]．教育理論與實踐，2018，38（17）：3–6．

[15] COOPER B, DUNNE M. Anyone for tennis? Social class differences in children’s responses to national curriculum mathematics testing [J]. The Sociological Review, 1998, 46 (1): 115–148.

[16] 陸璟．PISA測評的理論和實踐[M]．上海：華東師范大學出版社，2013：127–148．

[17] 李清，王菡．元認知策略、解題策略對不同層次學生數學問題解決影響的實證研究[J]．教育理論與實踐，2017，37（35）：41–43．

[18] 劉星辰，原露，陳啟山．數學焦慮與數學自我效能感對數學素養的影響：來自PISA的結果[J]．考試研究，2016（2）：89–94．

[19] 陳燕，羅增儒，趙建斌．從認知負荷理論看數學錯誤[J]．數學教育學報，2009，18（4）：19–22．

[20] 常磊，鮑建生．情境視角下的數學核心素養[J]．數學教育學報，2017，26（2）：24–28．

[21] 史寧中．試論數學推理過程的邏輯性——兼論什么是有邏輯的推理[J]．數學教育學報，2016，25（4）：1–16．

Identification and Analysis of Mathematical Errors in Solving Contextualized Problems

DENG Hai-ying1, YAN Qing2, WEI Ya-nan3

(1. School of Mathematics and Computational Science, Hunan First Normal University, Hunan Changsha 410205, China;2. Faculty of Mathematics and Statistics, Hubei University, Hubei Wuhan 430062, China;3. School of Mathematical Sciences, Nanjing Normal University, Jiangsu Nanjing 210046, China)

In problem solving, making errors are inevitable. The appropriate use of mathematical errors has gradually been recognized by educators as an effective teaching resource. Contextualized problem solving is closely related to key competency in mathematics. This paper developed a framework for error analysis of in solving contextualized mathematical problems. It is found that: (1) Among the six components of key competency of mathematics, mathematical abstraction and logical reasoning errors occur most frequently; and (2) in the three levels of key competency of mathematics, it is generally difficult to reach the second level. Research has also shown that the key factor in error making is not understanding the context. Teachers should deepen students’ understanding of the context and cultivate their ability to transfer knowledge in the context to promote the cultivation of mathematical key competency.

mathematical contextual problem solving; error analysis and evaluation; key competency of mathematics; context

附錄：測試題

1. 每年的7月1日—7月30日富士山對公眾開放，在這段時間里，大約有9?000名游客去富士山爬山，平均每天大約有名游客．

2. 學校剛剛舉行了秋季運動會，短跑競賽的競爭非常激烈．下表列出了進入決賽的5名同學的短跑成績，則跑道的同學是冠軍．

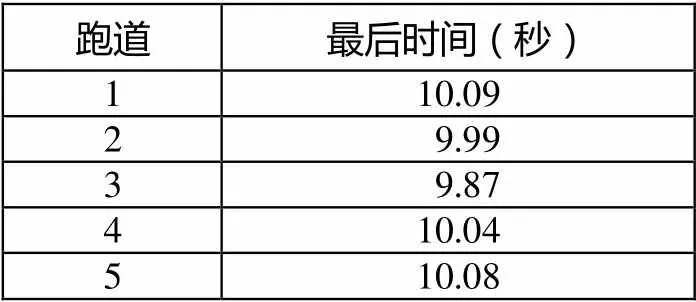
跑道最后時間（秒） 110.09 2 9.99 3 9.87 410.04 510.08

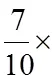
4. 體育中心距離學校17千米，一大型超市距離學校8千米，請問體育中心和超市有多遠？

5. 紅色、綠色和藍色被稱為光的三原色．在電子設備中我們通過調節這3種顏色的亮度表示其他顏色．用3個255以內的整數分別表示紅色、綠色和藍色的亮度，數字越大代表亮度越高．例如：(255, 0, 0)是指紅色，(0, 255, 0)代表綠色．(0, 255, 255)表示紅光亮度0、藍光亮度255、綠光亮度255，合起來就是標準青色；(200, 0, 150)表示紅光亮度200、綠光亮度0、藍光亮度150，合成的顏色是偏紅的紫色．(255, 255, 255)表示紅光亮度255、綠光亮度255，藍光亮度255合起來是白色．紅色和綠色可以合成黃色．標準黃色可由亮度最高的紅光和最高的綠光合成，請問：

（1）如何表示“標準黃色”?（2）如何表示“偏紅的黃色”？

6. 小明的爸媽趁著假期帶著小明和妹妹到花博園游玩．園內人山人海，每個展館幾乎都要排隊．大家討論決定要去參觀夢想館和流行館．每個展館的排隊方式都是兩人并排，地面畫有小型圓圈，工作人員會請排隊人群站在小型圓點上，以便統計人數．如右圖：

問題（1）：首先，小明一家人來到夢想館，小明他們所排位置旁的告示牌寫著離入口處大約需要2小時．而工作人員平均每十分鐘放30人同時入場，請問排在小明一家人前面的大約有多少人？

問題（2）：小明一家人來到流行館．小明發現排隊位置上寫的第101排，而工作人員平均約每10分鐘開放20人同時入場．請問，小明一家人還要等多久才能夠入場？

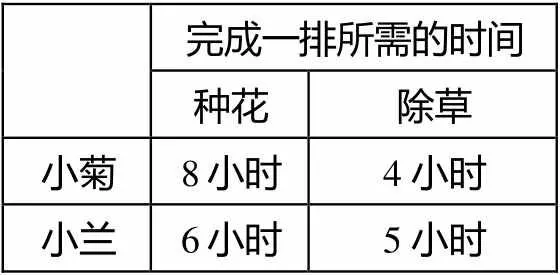
完成一排所需的時間 種花除草 小菊8小時4小時 小蘭6小時5小時

7. 小菊和小蘭應征園丁的工作，花園老板發現二人的工作態度都很好，對薪水的期待也相同．在完成一件需要種花和除草的工作中，老板比較二人種花和除草所需的時間如右表，請回答下列問題：

問題（1）：如果你是花園的老板，需聘用一位專職種花的人，每天工作10小時，你會請哪一個人幫你種花？請說明理由．

問題（2）：如果花季的臨時工，工資是以種花或除草的數量計算（例如種花或除草的工資都是5元/株），就小蘭而言，同樣的加班時間，她應該選擇種花還是除草的工作賺得比較多？

問題（3）：如果你是花園的老板，只能聘用一人負責種花與除草，若一個月的工作約需種10排花、每排要除4次草，你會聘用誰？請說出理由．

8. 翰子老師有一塊長方形的花，長15米、寬10米，如下圖：

將花圃以長方形表示，=15 m，=10 m．若翰子老師欲將郁金香、百合花、玫瑰花分別種滿花圃總面積的1/3，則有什么方式可以將此花圃面積三等分？請你幫翰子老師設計一下．（至少兩種方案，越多越好）

9. 蔡老師上班的概況如下，家里大門口出發到第一個紅綠燈下約2 km，再開到第二個紅綠燈下約3 km，第二個人紅綠燈即上高速公路，路程約15 km，下高速公路后，會遇到第三個紅綠燈，再開到上班的辦公大樓約20 km，這之間還有一個紅綠燈．蔡老師遵守交通規則，平常開車習慣是：一般限速70 km/小時的道路，蔡老師會開60 km/小時，高速公路限速110 km/小時，蔡老師會開100 km/小時．道路紅綠燈需要等2分鐘．

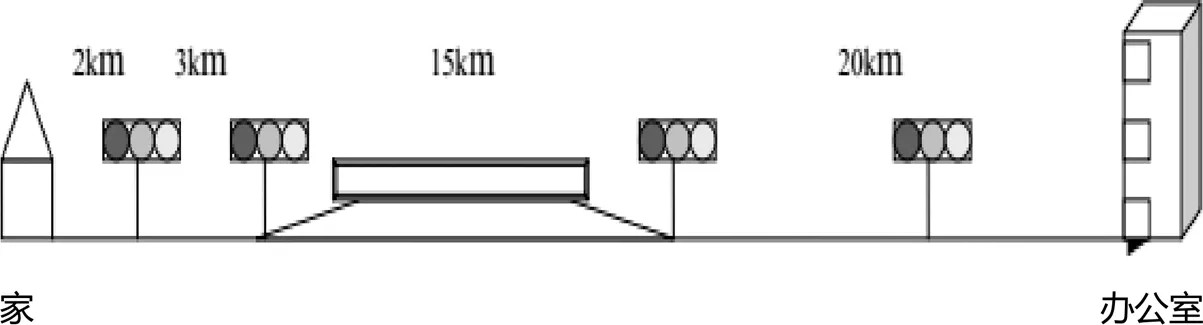
請根據以上信息，自己設計一個情境，可以增加條件，提出一個數學問題并解答．

G622

A

1004–9894（2021）01–0061–07

鄧海英，嚴卿，魏亞楠．數學情境問題解決錯誤分析與評價[J]．數學教育學報，2021，30（1）：61-67．

2020–10–09

湖南省社會科學成果評審委員會項目——小學生情境問題解決能力培養研究（XSP21YBC052）

鄧海英（1982—），女，湖南邵陽人，講師，碩士，主要從事課程與教學論和小學數學教育研究．

[責任編校：周學智、張楠]