視覺測量中環狀編碼標記點檢測與識別方法

左承林， 馬 軍， 岳廷瑞

(中國空氣動力研究與發展中心 低速空氣動力研究所，四川 綿陽 621000)

基于立體視覺技術進行三維測量時，需要對不同視角拍攝獲取的圖像進行特征提取和立體匹配，以計算被測物體的三維信息。匹配的精度直接影響著最終的測量精度，因而需要高精度的匹配算法。但是，傳統立體匹配方法計算復雜度高，匹配精度也較低，難以適用于高精度測量應用中。為此，通常使用編碼標記點作為被測物體的特征點，其具有唯一的編碼標識信息，便于檢測和識別，可實現不同視角圖像的高精度匹配。

到目前為止，已有眾多種類的編碼標記點被設計應用于視覺三維測量中[1-7]。具有代表性的編碼標記點有：環狀編碼標記點、點狀編碼標記點、方形編碼標記點、分布式編碼標記點、彩色編碼標記點、可糾錯編碼標記點、雙環象限編碼標記點、漢字編碼標記點等。其中，環狀編碼標記點具有仿射不變、平移旋轉不變、尺度不變等特性，易于檢測識別，因而被廣泛應用于視覺三維測量中。

編碼標記點檢測識別包括標記點中心定位和編碼環解碼兩個步驟，其中，中心定位是關鍵，也是編碼環解碼的基礎。圍繞著提高解碼精度和速度，國內外研究者進行了大量的研究。Forbes等[8]采用Canny 算子提取圖像輪廓，然后基于尺寸準則、形狀準則提取中心標記點擬合橢圓，再根據灰度準則讀取編碼帶信息進行解碼。Chen等[9]針對像素較小或投影角較大的編碼標記點，提出一種利用灰度梯度提取各編碼段中心角的檢測算法，能實現準確定位與解碼。宋麗梅等[10]和周玲等[11]基于環狀編碼標記點的仿射不變特性，分別通過坐標變化的方式將成像橢圓變換成直線和單位圓，實現了環狀編碼標記點的解碼識別。楊忞等[12]為提高標記點定位精度，利用擬合橢圓外切矩形的幾何性質來確定橢圓的長短軸位置和旋轉角度，進一步構造驗證參數，并結合聚類算法，最終提取有效的標記點類。此外，秦大輝等[13]將YOLO v3目標檢測網絡應用到了編碼標記點檢測定位中，提出了一種基于YOLO v3改進網絡識別編碼標記點，再通過距離判斷確定中心標記點的定位方法，最終獲得了較好的檢測識別效果且該方法魯棒性好。

針對視覺測量中環狀編碼標記點的檢測識別問題，本文提出了一種基于編碼環采樣的解碼識別方法。首先，使用Canny算子對圖像進行邊緣檢測，提取圖像的輪廓結構信息；然后，基于尺寸和形狀準則約束，初步濾除非標記點輪廓；使用Otsu算法[14]進一步提取標記點邊緣環狀鄰域，通過最小二乘橢圓擬合求解橢圓參數，并通過橢圓參數約束，再次進行非標記點輪廓濾除；最后，通過對編碼環進行360°采樣，解算獲得編碼值，實現標記點的解碼識別。

1 編碼標記點設計

本文使用的編碼標記點為8位環狀編碼標記點，結構如圖1(a)所示，其由中心圓和同心圓環構成，中心圓用于標記點定位，同心圓環則用于標記點編碼。編碼環根據實際需求可進行不同數量的等分，等分數量越多，編碼位數就越多，可產生的編碼標記點數量也就越多，通常使用較多的為8、12、15這3種等分數量的編碼標記點。編碼環編碼原理如圖1(b)所示，編碼環中每一個等分區域根據顏色的不同對應于“0”或“1”，整個編碼環對應于一個8位的二進制數。為了確保編碼值的唯一性，按逆時針方向逐位移動二進制數，其對應的十進制數中最小的十進制數即為編碼標記點的唯一編碼值。編碼環不同等分情況下的二進制數和標記點數如表1所示。

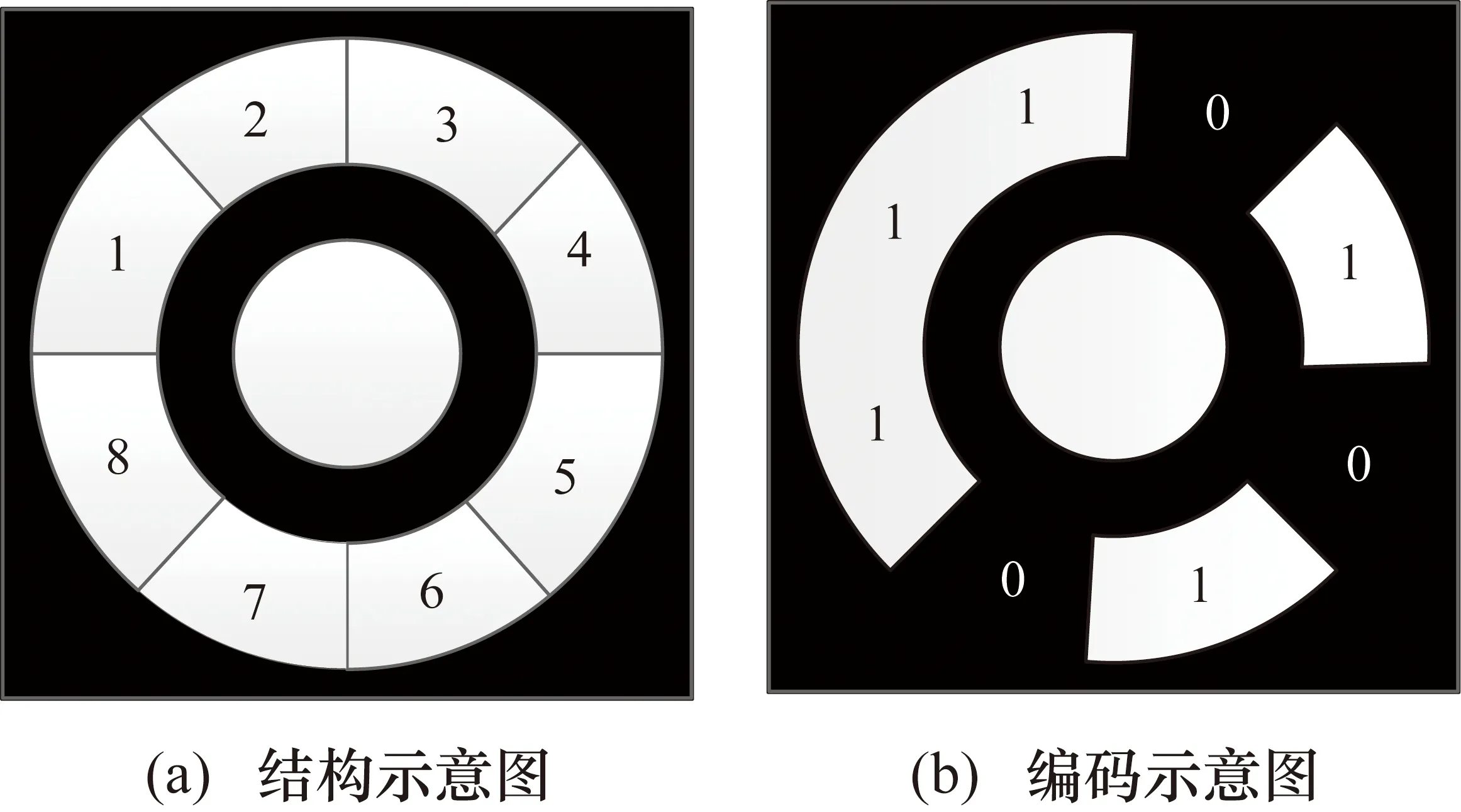
圖1 編碼標記點

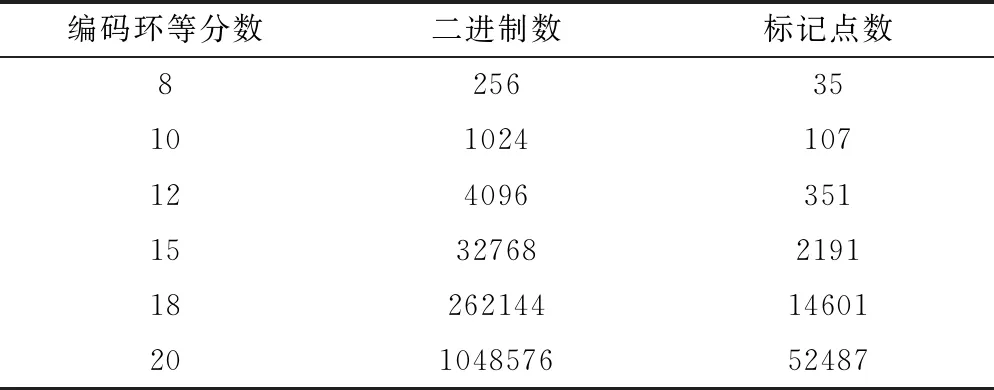
表1 編碼數、標記點數與二進制數關系表

2 編碼標記點檢測與識別

2.1 檢測定位

由于拍攝角度的影響，編碼標記點中心圓成像后通常呈橢圓形狀，對編碼標記點進行檢測定位即可確定中心圓在圖像平面上成像的橢圓中心。

首先采用Canny算子對圖像進行邊緣檢測，提取得到圖像的輪廓信息。然后，計算各邊緣輪廓的周長L、面積S和形狀因子G，通過設置合適的閾值，篩除不滿足閾值的輪廓，實現標記點的粗定位。其中，輪廓形狀因子G計算公式為

(1)

在標記點粗定位的基礎上，根據Otsu算法確定梯度閾值，提取得到標記點的邊緣環狀鄰域。與采用Canny算子得到的標記點單像素邊緣相比，標記點邊緣環狀鄰域對噪聲和不均勻光照條件具有更好的魯棒性。

為了得到成像中心圓的橢圓中心，需要對邊緣環狀鄰域進行最小二乘橢圓擬合。對于任意位置的橢圓，其一般方程表示為

f(x,y)=x2+Axy+By2+Cx+Dy+E=0

(2)

對邊緣環狀鄰域上的點進行最小二乘橢圓擬合，則目標函數為

(3)

式中，N為邊緣環狀鄰域上像素點個數。由極值原理可知，要使F最小，則必有：

(4)

通過式(4)即可解算得到橢圓方程參數A、B、C、D、E，進而可以計算得到：

(5)

式中，(x0,y0)，a，b，θ分別為標記點成像橢圓的中心坐標、長軸半徑、短軸半徑和偏角。由于尺寸和形狀約束不一定能完全濾去偽標記點，因此，基于擬合得到的橢圓參數進行了二次篩選，約束準則具體如下。

① 橢圓擬合偏差約束；

② 橢圓長短軸約束；

③ 橢圓長短軸比例約束。

當滿足上述約束準則后，橢圓輪廓即為標記點的成像中心圓，基于其橢圓中心坐標，即可實現標記點的精確定位。

2.2 解碼識別

由于編碼標記點成像符合仿射變換，圖像中心圓與編碼環仍然具有相同的中心和偏角，大小比例也不會發生變化。根據編碼標記點的物理尺寸和成像中心圓的橢圓參數，可計算得到成像編碼環的橢圓參數為

(6)

式中，R1和R2分別為編碼環的物理內環半徑和物理外環半徑；r為中心圓的物理半徑。

基于解算得到的成像編碼環橢圓參數，對編碼環進行采樣，如圖2所示。

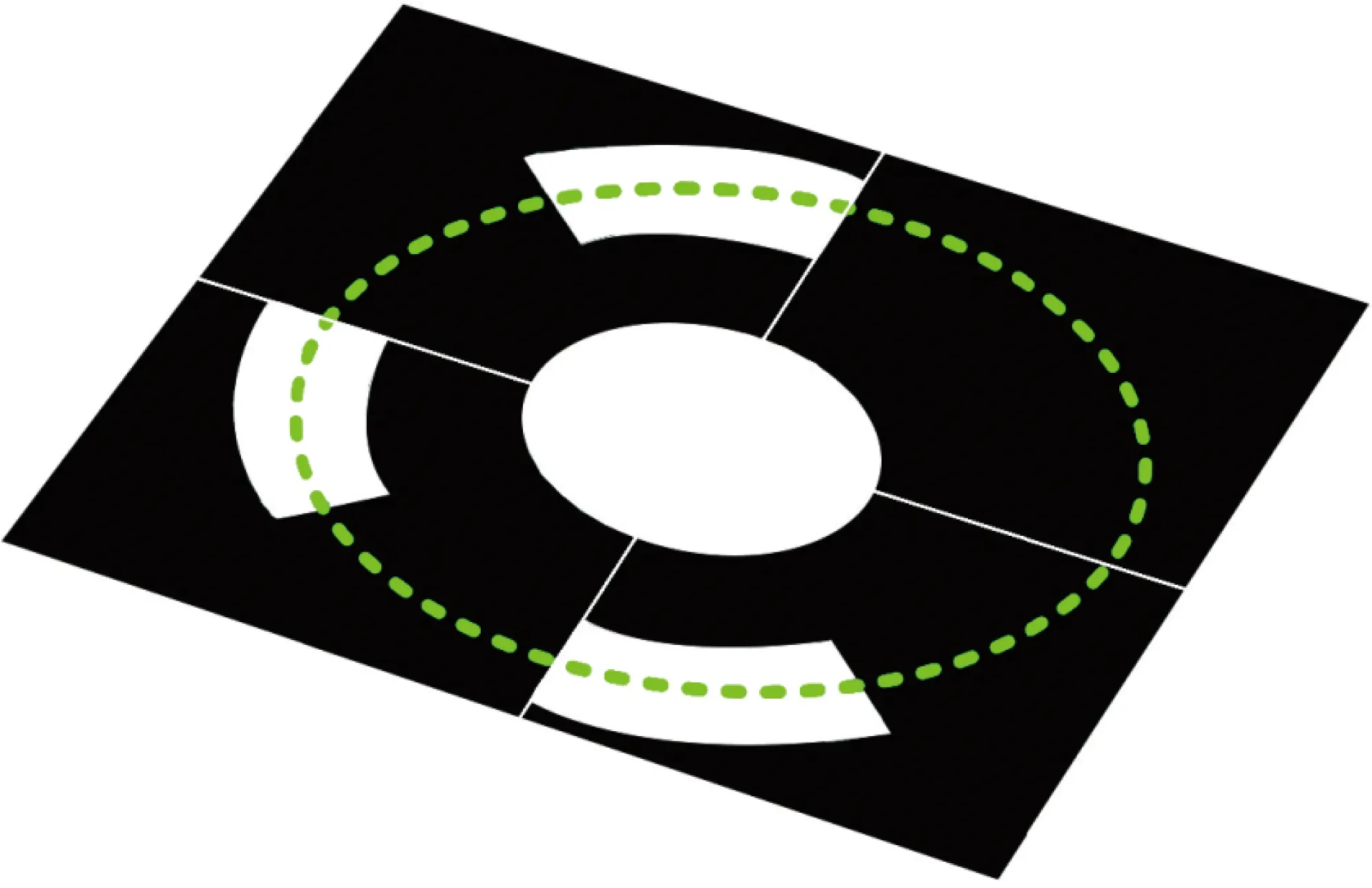
圖2 編碼環采樣

基于編碼環采樣的解碼識別具體步驟如下。

① 在編碼環上以任意位置為起點，按逆時針方向進行采樣，得到采樣序列Si= {si,1,si,2,…,si,j,…,si,k}。其中，i= 1,2,…,n為標記點編號；si,j為第i個標記點編碼環上的第j個采樣灰度值；k為采樣數量。

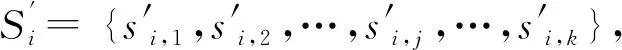
(7)

二值化處理方法如下：

(8)

(9)

式中，INT為取整函數；N=8為編碼標記點編碼環的等分段數；e=0.5為固定常數。

3 試驗結果與分析

為了驗證所提出的編碼標記點檢測識別算法的有效可行性，首先進行了模擬試驗，隨后，在直升機旋翼槳葉視覺測量風洞試驗中進行了實際應用。

3.1 模擬試驗

在室內燈光照明條件下拍攝得到的編碼標記點圖像如圖3(a)所示，相機成像傾角約為60°，每個編碼標記點旁邊都標注有相應的真實編碼值。從圖3(a)中可以看到，在較大成像傾角情況下，編碼標記點發生了較為明顯的變形，并且，局部區域還存在高反光情況。使用Canny算子進行邊緣檢測得到的圖像輪廓，如圖3(b)所示，基于尺寸準則、形狀準則和橢圓參數準則篩選后得到的標記點成像中心圓輪廓如圖3(c)所示，可以看到，經過篩選后，其他偽標記點輪廓得到了有效濾除。最終的解碼識別結果如圖3(d)所示，所有編碼標記點都得到了正確解碼識別，這說明本文所提出的算法對于成像變形和光照不均具有較好的魯棒性。

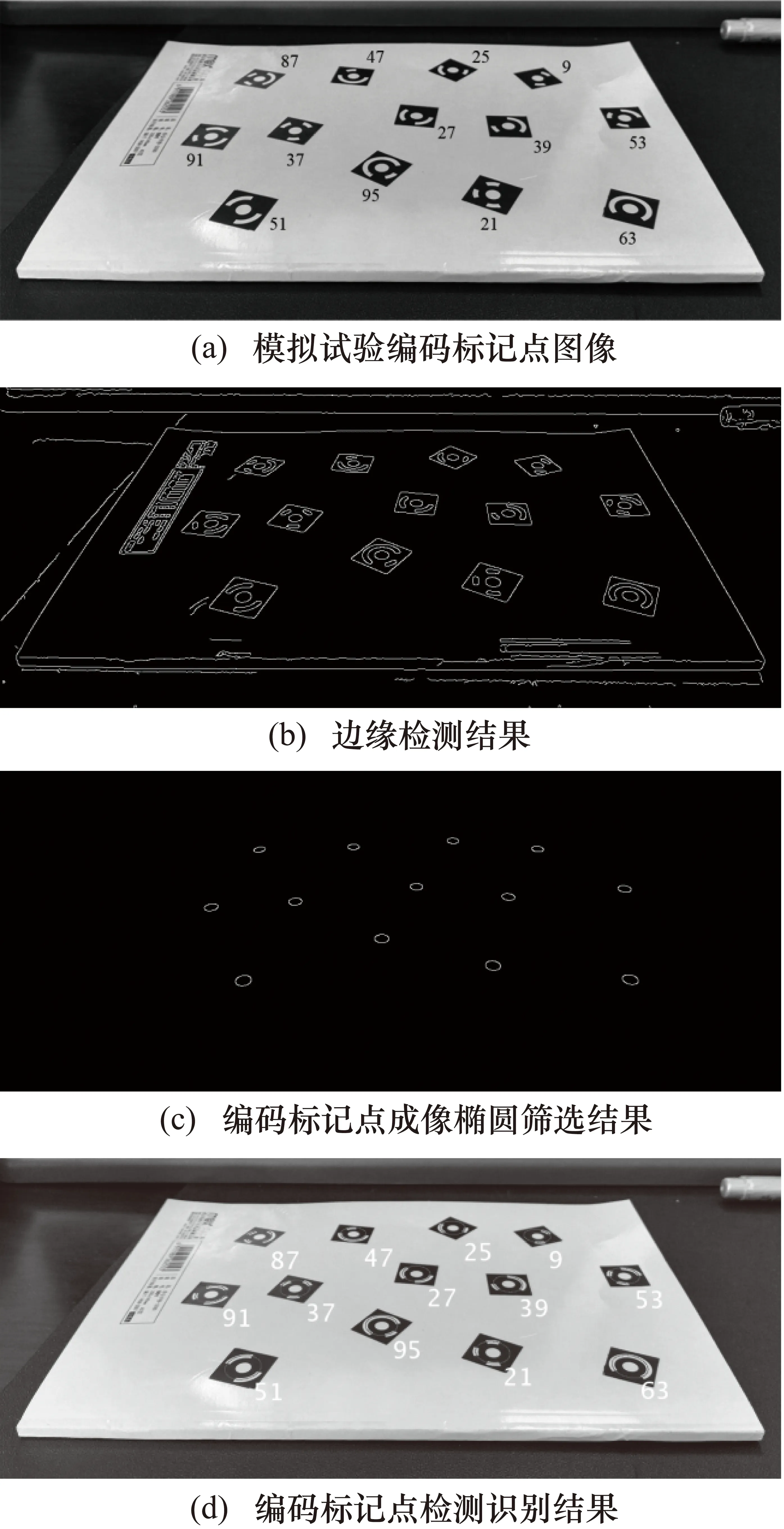
圖3 模擬試驗

3.2 直升機旋翼槳葉視覺測量風洞試驗

在中國空氣動力研究與發展中心Φ3.2 m風洞開展的Φ2 m直升機旋翼槳葉視覺測量風洞試驗如圖4所示，其中一片槳葉下表面上共布置有20個編碼標記點，其沿槳葉展向成對等距分布，每對編碼標記點之間的物理距離均為35 mm。測量系統由兩臺高速CCD相機構成，其被安裝固定在旋翼下方的試驗平臺上，確保了試驗過程中相機不會因為旋翼高速旋轉而發生振動。兩臺相機的成像分辨率為1024像素×1024像素，圖像位數為12-bit，最大幀頻為3.6 kHz。相機之間的光軸夾角約為30°，距離旋翼約2.5 m，測量視場約為1 m×1 m，可覆蓋旋翼一個象限的旋轉范圍。為了能夠拍攝得到清晰的旋翼槳葉瞬態圖像，試驗采用了高頻激光器進行瞬態照明，其波長為527 nm，能量為2×30 mJ@1 kHz，脈沖寬度為150 ns。試驗中，高頻激光器通過激光擴束鏡形成體激光，其照明區域覆蓋相機測量視場范圍；基于同步控制器、高速CCD相機和高頻激光器進行時鐘同步，根據旋翼編碼器信號，同步觸發高頻激光器和高速CCD相機進行瞬態照明成像。該試驗對旋翼高速轉速下不同槳葉傾角工況的編碼標記點進行了檢測識別。

圖4 直升機旋翼槳葉視覺測量風洞試驗

高速CCD相機拍攝得到的旋翼槳葉圖像如圖5(a)所示，為了不產生圖像拖影，成像系統采用了強照明、高速曝光的成像方式，因此，高反光特性的編碼標記點成像結構清晰，而背景則幾乎看不到，這極大地提高了編碼標記點檢測識別的準確性和魯棒性。圖像邊緣檢測結果和編碼標記點成像中心圓輪廓篩選結果如圖5(b)和5(c)所示。不同槳葉傾角條件下編碼標記點的解碼識別結果如圖6所示，可以看到，所有編碼標記點都得到了正確解碼識別，這說明槳葉傾角變化并不會影響編碼標記點檢測識別的準確性。

圖5 旋翼槳葉編碼標記點檢測定位

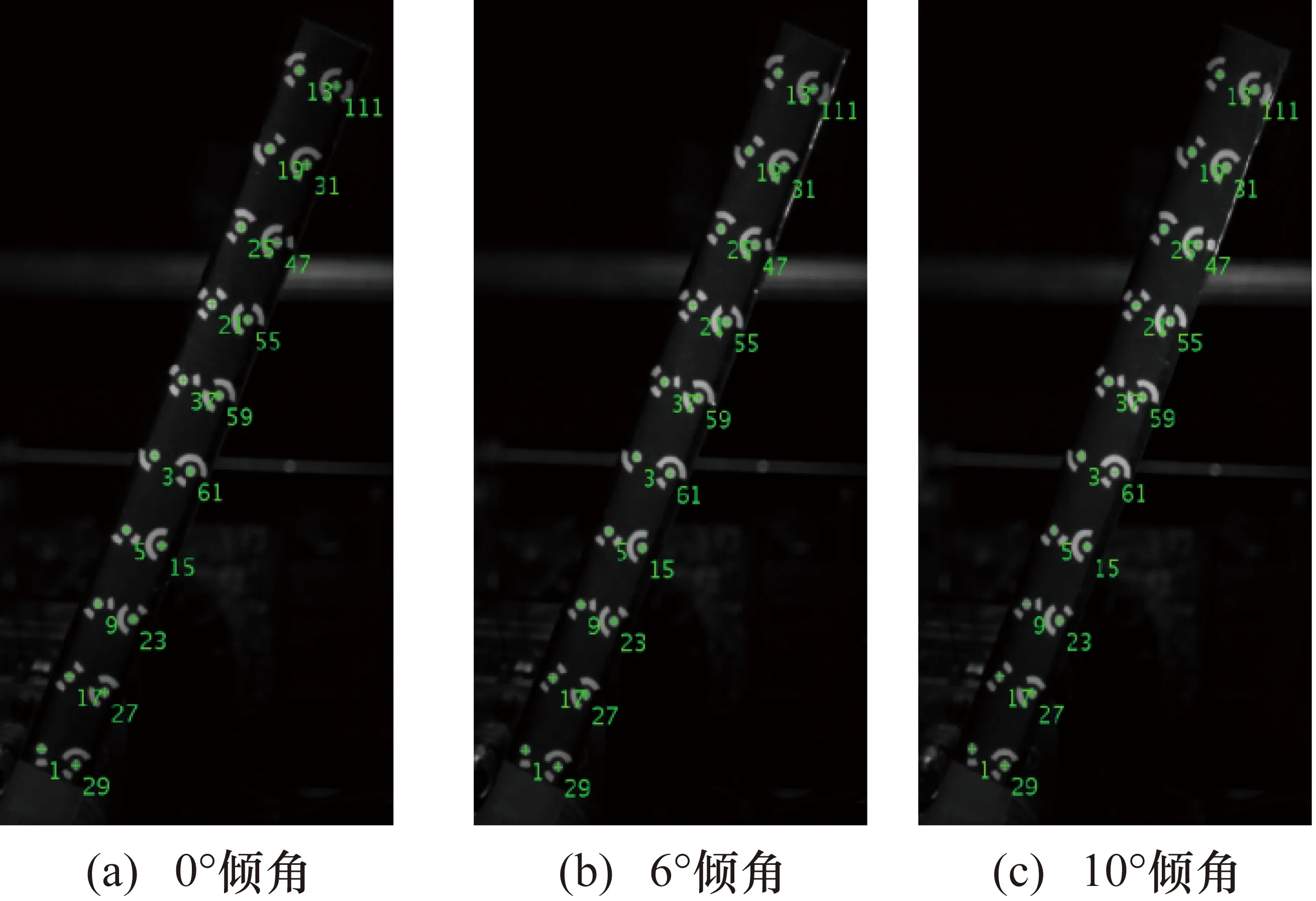
圖6 旋翼槳葉編碼標記點解碼識別

通過編碼標記點解碼值進行立體匹配解算得到的三維測量結果如圖7所示。基于測得的所有工況下編碼標記點對之間的三維空間距離，對測量精度和準度進行計算，結果如表2所示。表2雖然反映的是整個系統的測量精度，但也從側面驗證了本文所提出的算法的準確性。

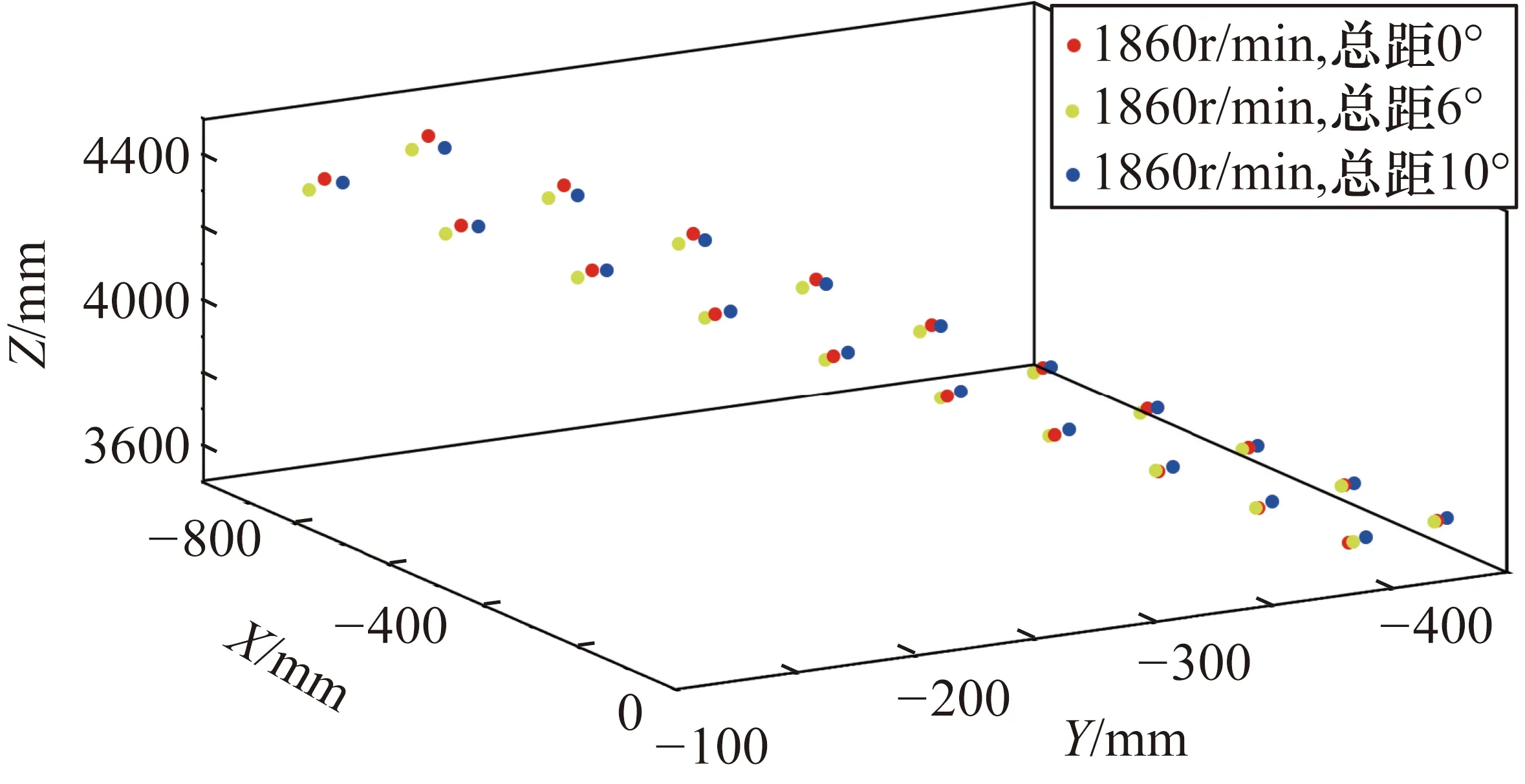
圖7 旋翼槳葉編碼標記點三維測量結果

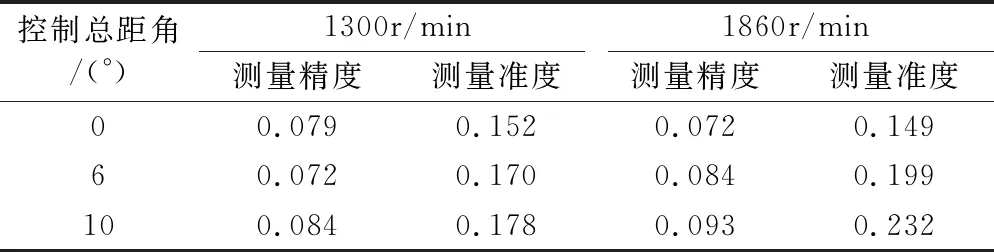
表2 不同轉速下測量精準度 單位：mm

4 結束語

視覺測量中，編碼標記點識別的準確性和魯棒性對后續的三維重建有著非常重要的意義。本文針對目前廣泛使用的環形編碼標志點，提出了一種基于編碼環采樣的檢測識別方法。試驗結果表明，所提出的算法受成像角度變化和光照不均等因素影響較小，編碼標記點檢測識別具有較高的魯棒性，實用性強。