激光追蹤測量系統機械結構動力學建模方法

李長亮， 陳洪芳， 孫若水

(北京工業大學 北京市精密測控技術與儀器工程技術研究中心，北京 100124)

隨著現代工業技術的發展，大型工件檢測、計算機輔助設計(CAD)對比測量、機器人校準等領域對測量的精度、范圍和實時性等方面都提出了更高的要求，激光精密跟蹤測量技術發揮著越來越重要的作用[1-3]。激光追蹤測量系統具有高精度、高效率、無接觸動態測量等優點，被廣泛應用于現代工業機床的在線校準、精密機構的裝配和工業產品的合格性檢測等方面。國外對激光追蹤測量技術的研究較為成熟，美國的Chesapeake公司研制了CMS-1000型六站距離交會激光跟蹤測量系統，測量精度達到了7～70 μm[4]。2005年德國國家計量研究院和英國國家物理實驗室聯合研發了一臺高精度的激光追蹤儀,此后，德國Etalon公司推出了Laser Tracer-NG激光追蹤儀,Laser Tracer-NG追蹤半徑在0.2～15 m范圍內，追蹤速度可達600 mm/s，測距分辨力為0.001 μm[1]。國內常放等[5]提出了一種基于WinCE的目標跟蹤控制系統，利用GPS模塊獲取目標方位，實現了跟蹤功能。2016年董登峰等[6]研究了激光跟蹤儀的跟蹤伺服控制系統并給出了總體設計方案，將角度測量精度提高到1.5″，可實現的最遠跟蹤距離不小于41.7 m。2017年張東坡等[7]設計了基于視覺伺服的目標跟蹤控制系統，實現對特定顏色目標的實時跟蹤控制，粗跟蹤精度可達38×10-6rad[8]。目前，我國高端測量的精密儀器研發基礎仍然十分薄弱，激光追蹤測量技術發展遲緩，國內科研和商用的激光追蹤設備還主要依賴進口，特別是高精度、高檢測速度、高經濟性的追蹤儀已經成為制約我國一系列重大裝備研制的瓶頸問題[9-12]。

本文提出一種基于激光追蹤測量系統機械結構的動力學建模分析方法，將拉格朗日動力學分析方法引入到激光追蹤測量系統機械結構設計分析中，為機械結構的設計改進和電機的精確選型提供了建議。

1 激光追蹤測量系統機械結構模型簡化

激光追蹤測量系統選用位置固定且不參與運動的標準球作為反射機構，不涉及角度測量,將誤差源引入減少到最少，提高了空間追蹤測量的效率和精度。激光追蹤測量系統主要由機械結構、伺服控制系統、光路系統和信號采集系統四大部分組成。機械結構作為激光追蹤測量系統的關鍵部件之一，是激光追蹤測量系統的基礎，也是激光追蹤測量系統的執行結構。其主要由底座、兩個精密轉軸軸系和兩個伺服減速電機、光學系統支撐板和光學元件以及標準球調節座組成。其機械結構的性能和動態特性以及機械結構的參數都會影響測量系統的準確度和精確度[12]。運用拉格朗日分析力學的方法研究其動態特性，在設計開發中對激光追蹤測量系統機械結構進行建模分析。

對完整激光追蹤測量系統進行動力學和力學分析的過程較為復雜，也存在很多影響較小但處理復雜的部件，通常應對其完整模型進行簡化處理。圖1為激光追蹤測量系統機械結構的完整模型，圖2為激光追蹤測量系統機械結構的簡化模型。

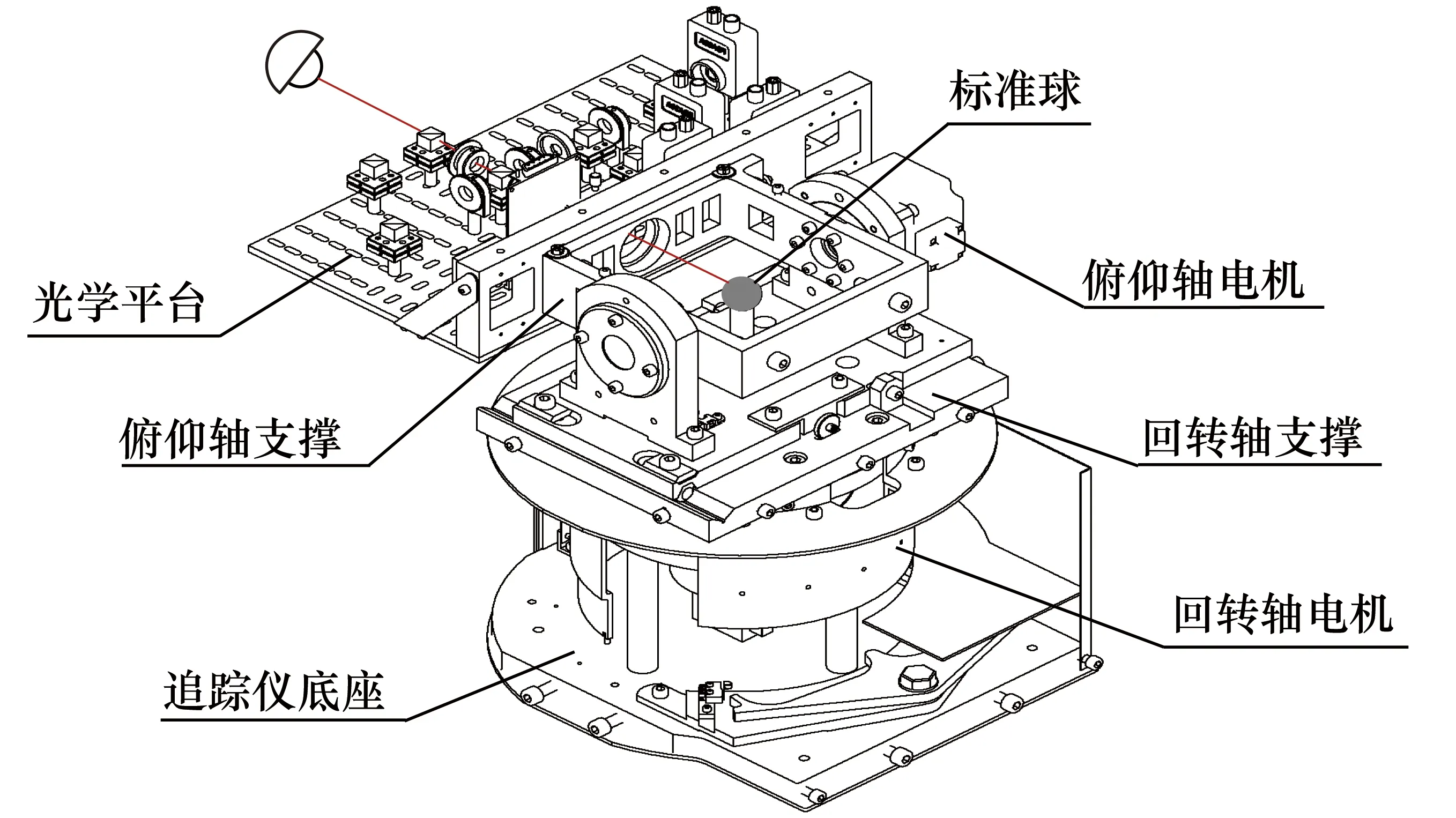
圖1 激光追蹤測量系統機械結構完整模型

圖2 激光追蹤測量系統機械結構簡化模型

由于低階模態對結構的性能影響較大，選取第1～6階固有頻率進行研究，通過ANSYS Workbench進行模態分析,得到完整和簡化模型前6階固有頻率的結果如表1所示。

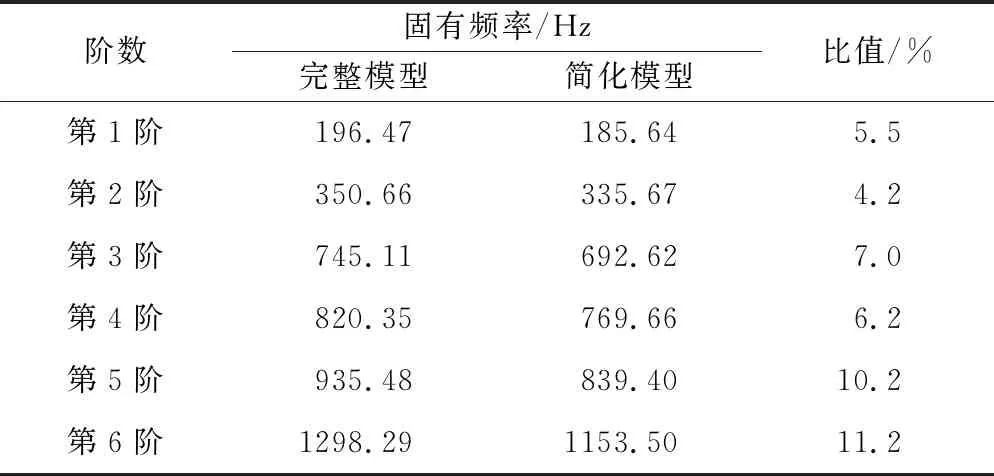
表1 前6階固有頻率對比

對完整模型和簡化模型進行振動頻率對比分析,如圖3所示，得到固有頻率的最大差異為11.2%,模型簡化處理在合理范圍內。

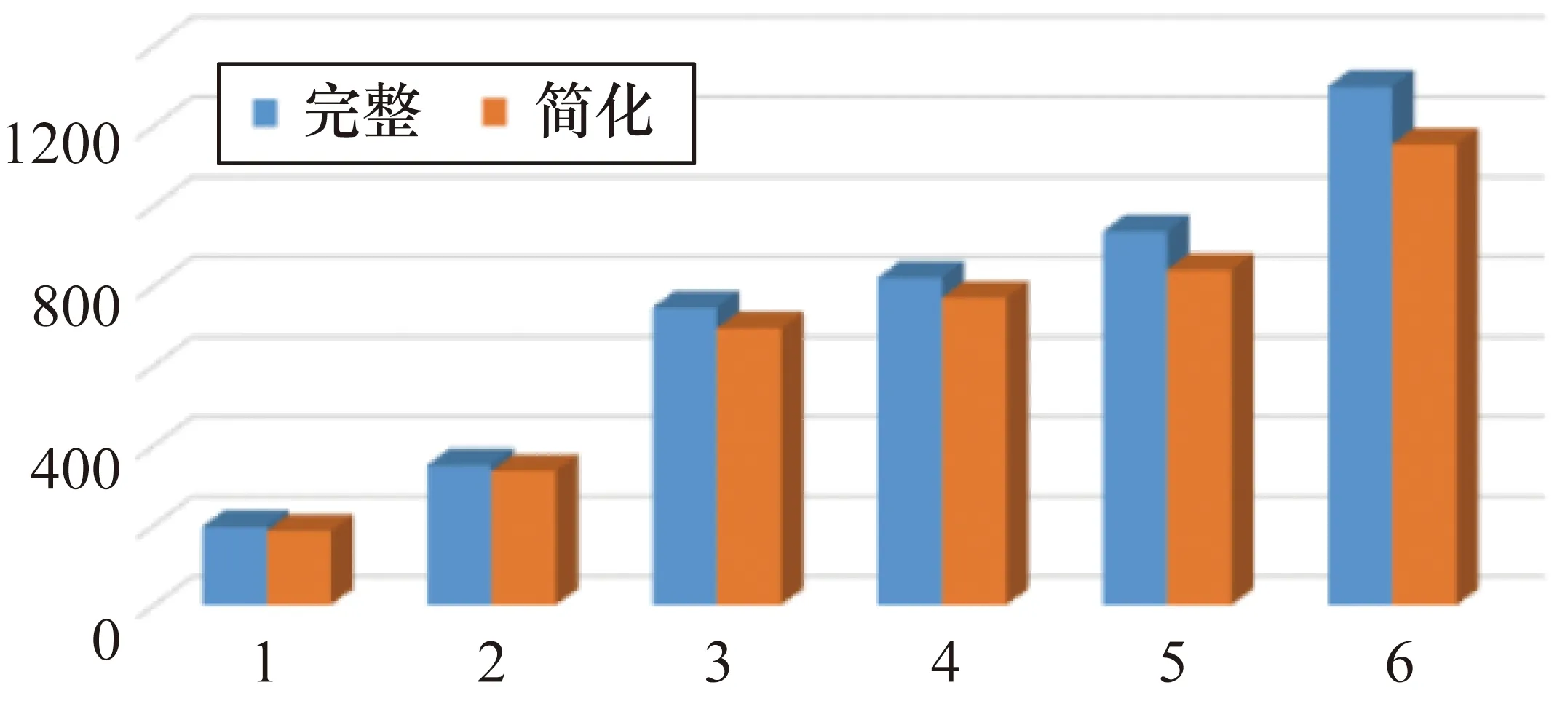
圖3 完整模型和簡化模型前6階振動頻率對比

2 系統機械結構的動力學建模

對激光測量系統機械結構進行動力學建模分析，分別考慮理想情況下和引入誤差項的非理想情況下的模型，對研究在運動過程中的關節電機力與力矩變化具有重要意義。

2.1 拉格朗日-歐拉動力學建模基礎

拉格朗日基于牛頓歐拉法創造了分析力學，其依賴廣義坐標和功能原理，不包含所有不做功的力和內部相互作用的力，把整個系統的動力學問題描述成一個封閉的數學表達式，其一般形式為

(1)

式中，qi為廣義坐標；T為動能；θj為廣義力。

拉格朗日方法具有較強的理論性和邏輯性，表示系統較簡潔。

拉格朗日函數被定義為系統的動能K和勢能P之差，即

L=K-P

(2)

K和P可以用任何方便的坐標系來表示。由拉格朗日函數所描述的拉格朗日-歐拉動力學方程[13]為

(3)

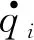
對于具有完整約束的兩自由度系統，可以得到兩個拉格朗日方程組。

2.2 激光追蹤測量系統機械結構理想動力學模型建立

對激光追蹤測量系統機械結構進行理想情況下的建模分析，不考慮結構參數誤差研究其動態特性。

2.2.1 激光追蹤測量系統機械結構理想D-H數學模型

建立機械結構的D-H數學模型為拉格朗日-歐拉動力學建模打基礎。

理想激光追蹤測量系統機械結構D-H模型的坐標系示意圖圖4所示。

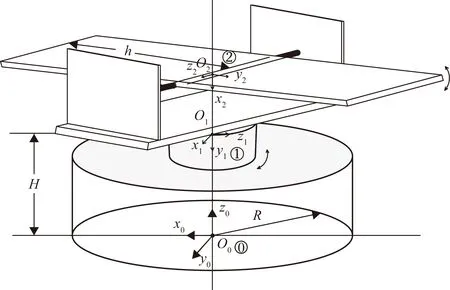
圖4 理想情況機械結構的D-H模型坐標系統

機械系統的坐標系廣泛采用直角坐標系，理想情況下回轉軸和俯仰軸交匯于一點，這一點在標準球的中心，按照D-H數學模型的建系規則建立如圖4所示的坐標系統。表2為理想激光追蹤測量系統機械結構的坐標系分配。

表2 機械結構D-H模型的坐標系分配

可以得到激光追蹤測量系統機械結構D-H模型的齊次變換矩陣為

(4)

(5)

(6)

式中，C1=cosθ1，S1=sinθ1,C2=cosθ2，S2=sinθ2。

式(6)為激光追蹤測量系統機械結構理想情況的D-H數學模型。

2.2.2 激光追蹤測量系統機械結構理想動力學模型

不考慮結構參數引入的誤差項建立機械結構的動力學模型。

根據兩自由度機械結構的動力學方程封閉形式：

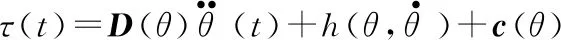
(7)

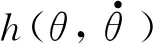
兩自由度慣性加速度相關的系統矩陣為

(8)

(9)

(10)

式中，J1，J2為回轉軸和俯仰軸的慣性矩矩陣。

U11=Q10A1

U21=Q10A2

U22=0A1Q21A2

式中，Qi,i=1,2為廣義坐標點。

激光追蹤測量系統兩個牽引軸的慣性矩為

(11)

(12)

式中，R為回轉軸電機驅動的上部構件的理想回轉半徑；m1為回轉軸電機驅動的上部構件的總質量；r為俯仰軸運動的俯仰旋轉半徑；m2為俯仰電機帶動做俯仰運動的構件總質量。

科里奧利力項和離心項如下：

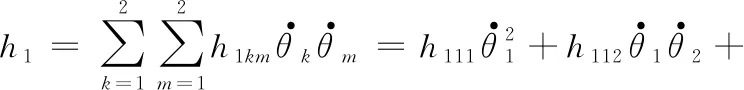
(13)

(14)

式中不同項的系數為

(15)

在激光追蹤測量系統進行目標追蹤的過程中沒有機械結構的平移運動只有旋轉運動，系統的動能只包括旋轉部分，因此無須考慮勢能的變化。

結合式(7)～式(10)和式(13)～式(14)，得到激光追蹤測量系統機械結構理想情況拉格朗日-歐拉動力學模型為

τ1τ2 =12m1R2+12m2r2S220012m2r2 θ··1θ··2 +

(16)

式中，τ1，τ2分別為回轉軸和俯仰軸的關節力矩。旋轉關節空間的動力學方程反映了關節力矩與關節變量、運動速度和加速度之間的函數關系，將力與運動結合在一起。

2.2.3 理想機械結構動力學模型的冗余項分析

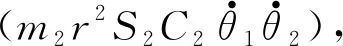
實際上，俯仰角θ2是由俯仰軸控制電機帶動跟蹤光學系統的旋轉角，其取值范圍在-15°～85°，可對S2C2構造函數求極值。在實際的追蹤過程及大多數的應用中，激光追蹤測量系統的追蹤速度相對較慢，設其跟蹤速度為0.03 rad/s。激光追蹤測量系統機械結構的工作參數如表3所示。

表3 激光追蹤測量系統機械機構的實際工作參數

基于上述激光追蹤測量系統實際工作參數，當激光追蹤測量系統在較低速度下工作時，理想動力學方程中的科里奧利力項和離心力項都遠小于第一項，因此在實際工作的情況下可以忽略不計。所以激光追蹤測量系統的機械結構理想的拉格朗日-歐拉動力學模型可以簡化為

τ1τ2 =12m1R20012m2r2 θ··1θ··2

(17)

可以看出，激光追蹤測量系統機械結構的理想動力學模型在實際工作情況下較為簡單，加速度參數對關節力的影響最大，在電機啟動時回轉軸和俯仰軸的力矩瞬間達到最大值，與實際情況相符。

2.3 激光追蹤測量系統機械結構非理想動力學模型建立

對激光追蹤測量系統機械結構進行非理想情況下的建模分析，考慮結構參數誤差研究其動態特性。

2.3.1 激光追蹤測量系統機械結構非理想D-H數學模型

任何機械結構都存在一定的非理想情況，激光追蹤測量系統機械結構的非理想情況主要指機械構件與電機回轉軸線存在的位置偏心和角度偏移，激光追蹤測量系統機械結構的非理想D-H模型坐標系統示意圖如圖5所示。

圖5 激光追蹤測量系統機械結構的非理想D-H模型坐標系統

考慮到非理想情況下的機械結構可能存在的角度偏移和位置偏移誤差，與理想情況不同，3個坐標系的原點不一定在電機的旋轉軸線上，點o0，o1和o2分別表示坐標系o0-x0y0z0，o1-x1y1z1和o2-x2y2z2的原點。按照D-H建模規則建立圖5所示的坐標系統，通過這種方式在模型中將角度偏移和位置偏移誤差包含在模型內。非理想激光追蹤測量系統機械結構的坐標系分配如表4所示。

表4 激光追蹤測量系統機械結構非理想情況的坐標系統D-H模型參數

對于實際的情況，坐標系2所在的激光追蹤測量系統光學平臺用于安裝追蹤系統的光學元件，由于軸心偏移方向平行于俯仰運動的旋轉軸，可忽略不計，位置偏移僅考慮底部回轉軸電機與頂部俯仰軸電機所在的旋轉軸線即可。可以得到Δθ2≈0和α2≈0。因此系統變換矩陣為

(18)

(19)

(20)

式中，C1=cosθ1，S1=sinθ1，Sα1=sinα1,C2=cosθ2，S2=sinθ2，Cα1=cosα1。

其中，式(20)為激光追蹤測量系統機械結構非理想的D-H數學模型。

2.3.2 激光追蹤測量系統機械結構非理想動力學模型

考慮激光追蹤測量系統機械結構參數引入的誤差項角度偏移和位置偏移,建立機械結構的非理想動力學模型。

慣性加速度相關的系統矩陣為

(21)

(22)

(23)

其中：

(24)

V12=a2[Sα1(a1C2+a2)+d2S2Cα1]

(25)

(26)

科里奧利力項和離心項如下：

(27)

(28)

式中，

(29)

F21=a2(d2Cα1C2-a1Sα1S2)

(30)

(31)

(32)

結合式(21)～式(23)、式(27)～式(28)和式(14)，得到激光追蹤測量系統機械結構非理想情況拉格朗日-歐拉動力學模型為

τ1τ2 =12[m1R2C2α1+m2r2(S2α1C22+S22)]+m2V1112m2r2Sα1+m2V1112m2r2Sα1+m2V1212m2r2+m2V22 θ··1θ··2 +[m2r2S2C2(1-S2α1)+2m2Cr]θ ·1θ ·2+m2F21θ ·22-12m2r2S2C2(1-S2α1)+m2F12 θ ·1+m2F22θ ·22

(33)

非理想旋轉關節空間的動力學方程反映了關節力矩與關節變量、速度和加速度之間的函數關系，并引入了相關誤差項，將力與運動結合在一起。

2.3.3 非理想機械結構動力學模型冗余項分析

非理想情況下激光追蹤測量系統機械結構的動力學方程太復雜，需要做進一步的分析處理。

耦合慣性項對于加速度有關項的影響取決于偏心角α1。因此，耦合慣性項的影響程度取決于激光追蹤測量系統機械結構的最大偏心角。激光追蹤測量系統機械結構中允許的最大偏心角α1max可以使用上面得出的機械結構的動力學模型來估算。

對于安裝在回轉軸電機上的機械結構的慣性項，最大偏心角的正弦值為

sinα1max≤0.05

耦合慣性項小于主慣性項的5%可以忽略不計[14]，則最大偏心角為

α1max≤3°

在激光追蹤測量系統機械結構中，由耦合慣性項引起的不良影響小于主慣性項的1%，可以忽略不計。

對于主慣性項，實際的a2和d2很小也可能不存在，取決于激光追蹤測量系統中的機械構件的加工和總體的安裝過程。實際系統中a2和d2的實際值小于1 mm，同樣與主要慣性項相比可以忽略不計。

科里奧利力項和離心力項如下：

(34)

(35)

因此，激光追蹤測量系統機械結構的非理想動力學模型可以簡化為

τ1τ2 =12(m1R2+m2r2S22)+(m1+m2)a210012m2r2 θ··1θ··2 +

(36)

由理想和非理想情況下的動力學分析可得，激光追蹤測量系統在實際應用中追蹤速度較低，經分析可以忽略所有科里奧利力項和離心力項的影響。激光追蹤測量系統機械結構屬于兩自由度系統，動力學模型為兩個相互獨立的方程，可見對每一軸系可以單獨進行分析和電機選擇。

3 分析與討論

根據激光追蹤測量系統動力學運動參數要求，運用ADAMS軟件分別仿真機械結構從靜止加速到追蹤速度過程和以勻速追蹤速度追蹤過程兩種情況下的關節力矩變化進行分析，激光追蹤測量系統簡化的機械結構ADAMS模型如圖6所示。

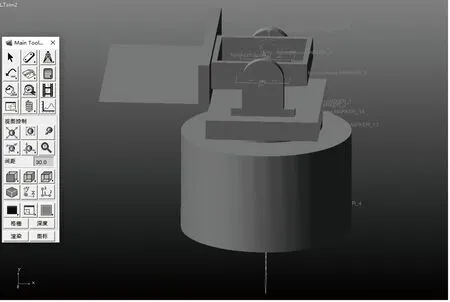
圖6 激光追蹤測量系統簡化結構的ADAMS模型

3.1 加速啟動過程

追蹤測量系統機械結構在控制系統的控制下從對準目標靶鏡的位置開始，要求在0.04 s的響應時間內達到勻速追蹤速度，相關參數設置見表5，研究兩軸力矩在啟動過程的變化。

表5 啟動過程運動參數

根據激光追蹤儀控制系統的設計要求，負載曲線如圖7所示。

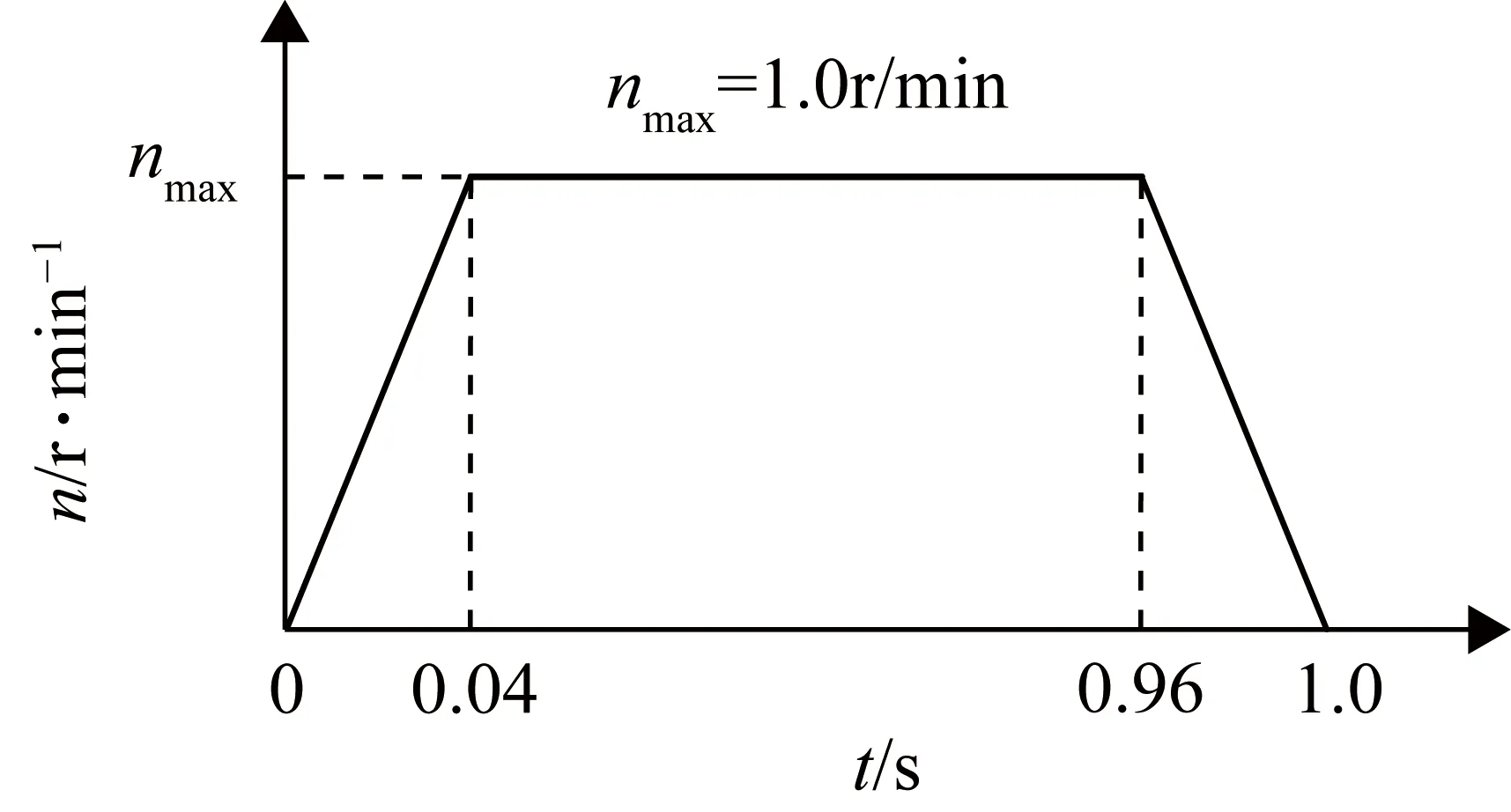
圖7 負載曲線

計算得到系統的運動參數如表5所示。

按照運動參數要求，在ADAMS中為激光追蹤測量系統機械結構的簡化模型運動關節添加驅動函數，具體如表6所示。

表6 ADAMS驅動輸入

得到回轉軸和俯仰軸的關節處驅動力矩變化曲線,如圖8、圖9所示。

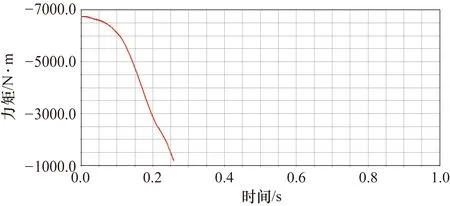
圖8 回轉軸驅動力曲線

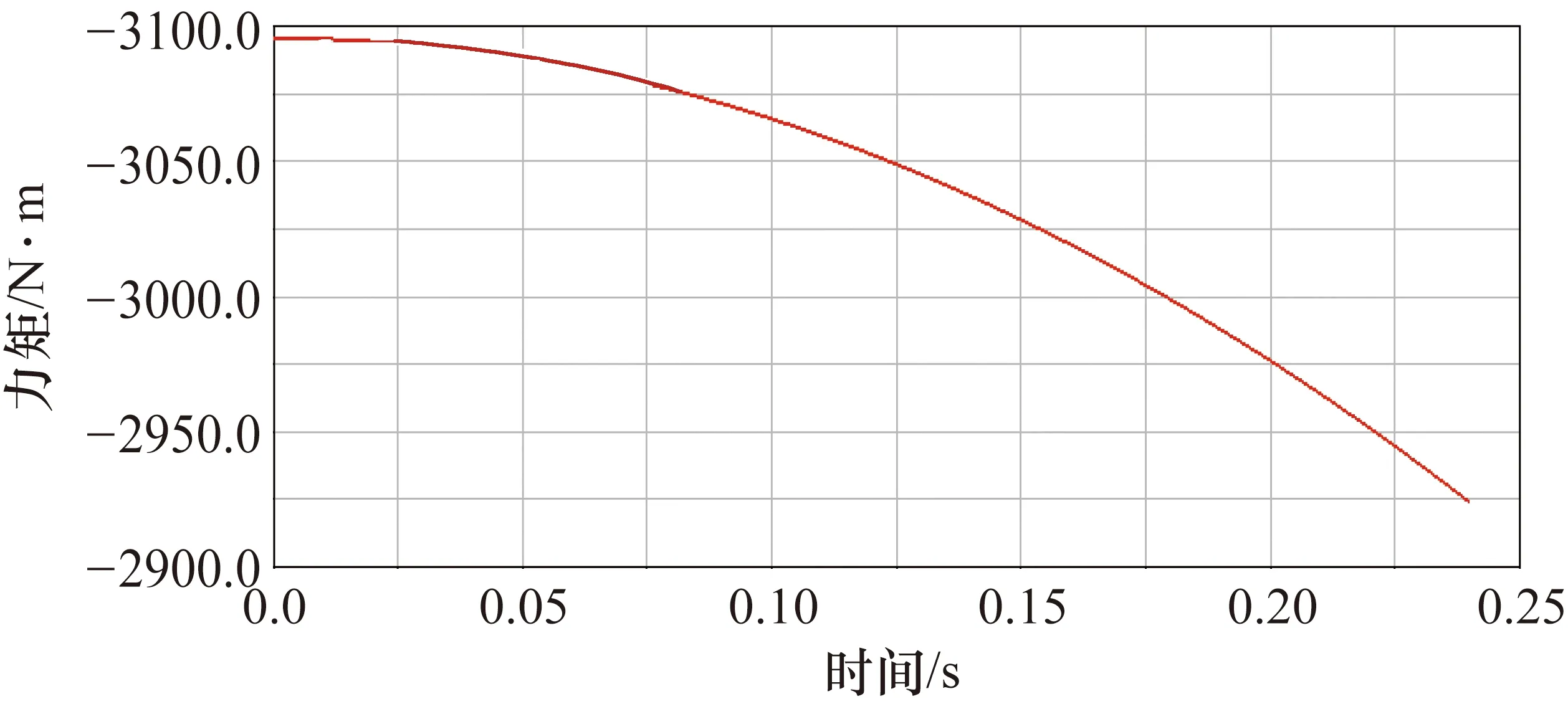
圖9 俯仰軸驅動力曲線

通過力矩變化曲線可以看出，在加速啟動的過程中，不考慮驅動力矩的方向,只研究前0.04 s其驅動力矩的最大值出現在t=0 s時刻，其對應的力矩最大值分別為：回轉軸T1max=6.8 N·m，俯仰軸T2max=2.8 N·m，最大驅動力矩出現在開始加速的瞬時，與模型分析一致，在機械結構的設計過程中須保證大于此力矩值的強度。

3.2 勻速追蹤過程

根據勻速追蹤過程運動參數表(如表7所示)，在ADAMS中為激光追蹤測量系統機械結構的簡化模型添加相應的關節驅動函數，具體如表8所示。

表7 勻速追蹤過程運動參數

表8 ADAMS驅動輸入

得到回轉軸和俯仰軸的驅動力矩曲線如圖10、圖11所示。

圖10 回轉軸驅動力曲線

圖11 俯仰軸驅動力曲線

由以上仿真結果可以看出，在勻速追蹤過程中，驅動力矩值為零，與所建的動力學模型一致。

對激光追蹤測量系統機械結構的動力學理想與非理想動力學建模進行分析，發現可以忽略機械結構參數引入的動態耦合項影響，通過ADAMS對機械模型的分析驗證了動力學數學模型的準確性。

4 結束語

本文提出了激光追蹤測量系統機械結構的動力學建模方法，通過對激光追蹤測量系統機械結構的理想和非理想動力學模型建立和簡化機械模型的ADAMS分析，可以得出以下結論。

① 激光追蹤測量系統機械結構中沒有顯著的動態耦合力，與動態耦合力相關的耦合項，例如科里奧利力項和離心力項在系統測量過程中可以忽略。

② 激光追蹤測量系統每一個運動軸系可以單獨建立動力學模型并可以單獨選擇合適的電機。