不確定性負虛系統(tǒng)的絕對穩(wěn)定性研究

陳 陣

(中國科學技術(shù)大學 信息科學技術(shù)學院，安徽 合肥 230026)

Lanzon和Peterson最早提出負虛系統(tǒng)這一概念，并且引起了很多系統(tǒng)理論研究者的關(guān)注[1-4]。在實際工程中，通過選取合適的系統(tǒng)狀態(tài)，系統(tǒng)的傳遞函數(shù)將表現(xiàn)出負虛性質(zhì)，例如大型車隊的編組控制、原子力顯微鏡納米懸梁臂定位系統(tǒng)、機械硬盤驅(qū)動器、Sallen-Key低通濾波器等都可以建模成具有負虛性質(zhì)的模型[5-7]。負虛系統(tǒng)考慮系統(tǒng)頻率響應(yīng)M(jω)的虛部的性質(zhì)，要求對于所有的ω∈(0,∞)，j(M(jω)-M(jω)*)≥0。

線性時不變(LTI)多輸入多輸出(MIMO)負虛系統(tǒng)互連的魯棒穩(wěn)定性已經(jīng)被廣泛研究[1-2,8-9]。并且，得到了傳遞函數(shù)為M(s)的負虛的被控對象和傳遞函數(shù)為N(s)的嚴格負虛的控制器的正反饋互連系統(tǒng)(如圖1所示)穩(wěn)定的充分必要條件，即DC增益條件[1]：

λmax(M(0)N(0))<1

(1)

式中，λmax(·)為一個只有實特征值的矩陣的最大的特征值。

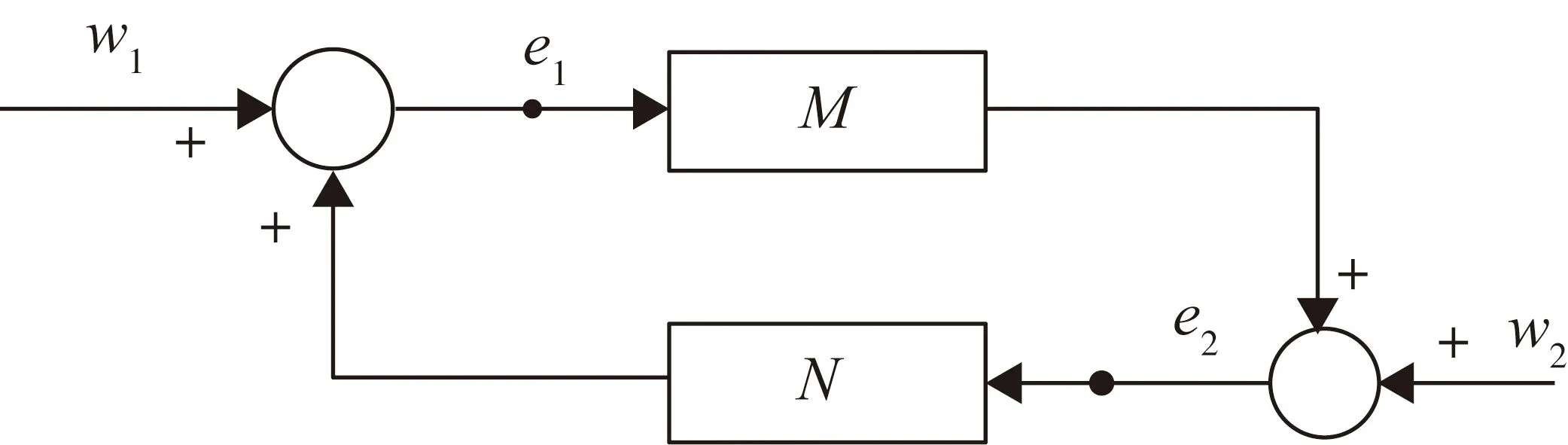
圖1 負虛反饋控制系統(tǒng)

近年來，負虛系統(tǒng)理論的研究被拓展到了無損負虛系統(tǒng)[10]、有混合性質(zhì)的互連系統(tǒng)的穩(wěn)定性研究[11]、控制器設(shè)計和性能分析[12]等各個方面。其中，假設(shè)所有狀態(tài)都可用于狀態(tài)反饋，針對具有嚴格負虛不確定性的系統(tǒng)，Song等[12]提出了一種基于狀態(tài)反饋的系統(tǒng)魯棒靜態(tài)反饋綜合方法，這是唯一的關(guān)于具有非線性的負虛性質(zhì)的研究，但由于要求非線性部分具有嚴格負虛性質(zhì)，具有較高的保守性。

絕對穩(wěn)定性定理保證了反饋路徑包含動態(tài)線性時不變系統(tǒng)和反饋路徑包含無記憶非線性系統(tǒng)的反饋系統(tǒng)的穩(wěn)定性。因此，絕對穩(wěn)定性定理為具有給定集合不確定性的系統(tǒng)的魯棒穩(wěn)定性的充分條件[13]。對絕對穩(wěn)定條件的進一步研究考慮限制在單調(diào)的、基于擴展的Lur’e-Postnikov李雅普諾夫函數(shù)的斜率有界時不變非線性性[14]。在實際工程系統(tǒng)中，普遍存在著斜率有界的無記憶不確定性，這是影響動態(tài)系統(tǒng)性能的一個重要因素[15-22]。因此，具有限斜非線性的系統(tǒng)的絕對穩(wěn)定性受到越來越多的關(guān)注[23]。

本文考慮一個負虛的被控對象，一個斜率有界、無記憶的不確定性和一個嚴格負虛的控制器互連的系統(tǒng)。提出的定理表明，對于上述系統(tǒng)，如果一些線性矩陣不等式成立，則閉環(huán)系統(tǒng)是絕對穩(wěn)定的。本文使用環(huán)變換的方法，擴展了無源性定理的效用。利用這些方法，整個閉環(huán)系統(tǒng)采用分解形式。在分解部分的基礎(chǔ)上，建立了連通的全局漸近收斂性，并建立了一個Lur’e-Postnikov李亞普諾夫函數(shù)，進而驗證了系統(tǒng)的絕對穩(wěn)定性。在負虛系統(tǒng)和不確定性已知的情況下，得到了使系統(tǒng)絕對穩(wěn)定的嚴格負虛控制器的DC增益條件。

1 問題描述

1.1 負虛系統(tǒng)

引理1[8]：設(shè)(A,B,C,D)是m×m維正則實有理傳遞函數(shù)矩陣R(s)的一個最小狀態(tài)空間實現(xiàn)，其中A∈Rn×n，B∈Rn×m，C∈Rm×n，D∈Rm×m，則R(s)是負虛的，當且僅當：

① det(A)≠0，D=DT；

② 存在Y=YT>0，Y∈Rn×n，使得

AY+YAT≤0且B+AYCT=0

(2)

引理2[8]：設(shè)(A,B,C,D)是m×m維正則實有理傳遞函數(shù)矩陣R(s)的一個最小狀態(tài)空間實現(xiàn)，其中A∈Rn×n，B∈Rn×m，C∈Rm×n，D∈Rm×m，則R(s)是負虛的，當且僅當：

①A是Hurwitz，rank(B)=rank(C)=m，D=DT；

② 存在Y=YT>0，Y∈Rn×n，使得

AY+YAT≤0且B+AYCT=0

(3)

1.2 斜率有界不確定性

將多個標量斜率有界的非線性以向量形式考慮在一起，將非線性算子的類[25]定義為

(4)

式中，AC(R+)為絕對連續(xù)函數(shù)f:R+→R構(gòu)成的空間。由于在變換后的非線性中需要建立一個無源關(guān)系，因此提出了扇形變換。

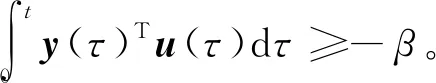
下面的定理給出了斜率有界無記憶的非線性性和無源算子之間的關(guān)系。

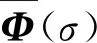
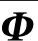
圖2 多個解耦非線性性，M=diag(μ1,μ2,…,μm)

定義2[26]：對于一個由線性系統(tǒng)部分和非線性部分反饋互連的系統(tǒng)，如果對于任意滿足扇形條件的非線性性，該系統(tǒng)在原點是全局一致漸進穩(wěn)定的，則稱這個系統(tǒng)是絕對穩(wěn)定的。

本文研究的是帶有不確定性的系統(tǒng)的絕對穩(wěn)定性，如圖3所示。假設(shè)外部輸入為0，其中x∈Rn，xc∈Rnc；u,y∈Rm，uc,yc∈Rmc。

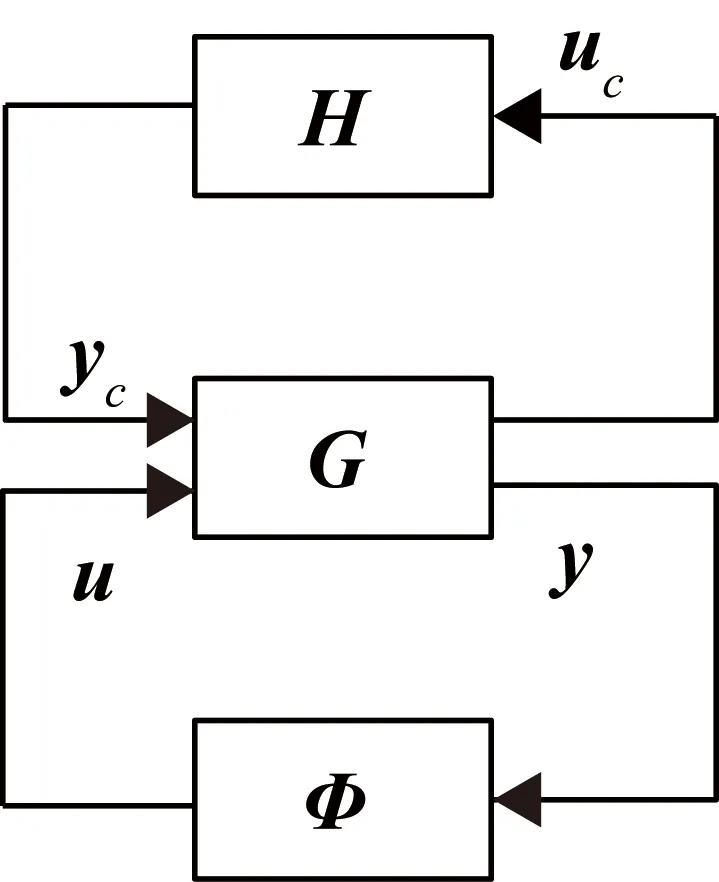
圖3 帶有斜率有界非線性性的反饋系統(tǒng)

圖3系統(tǒng)狀態(tài)空間方程為

(5)

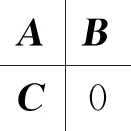
1.3 環(huán)變換

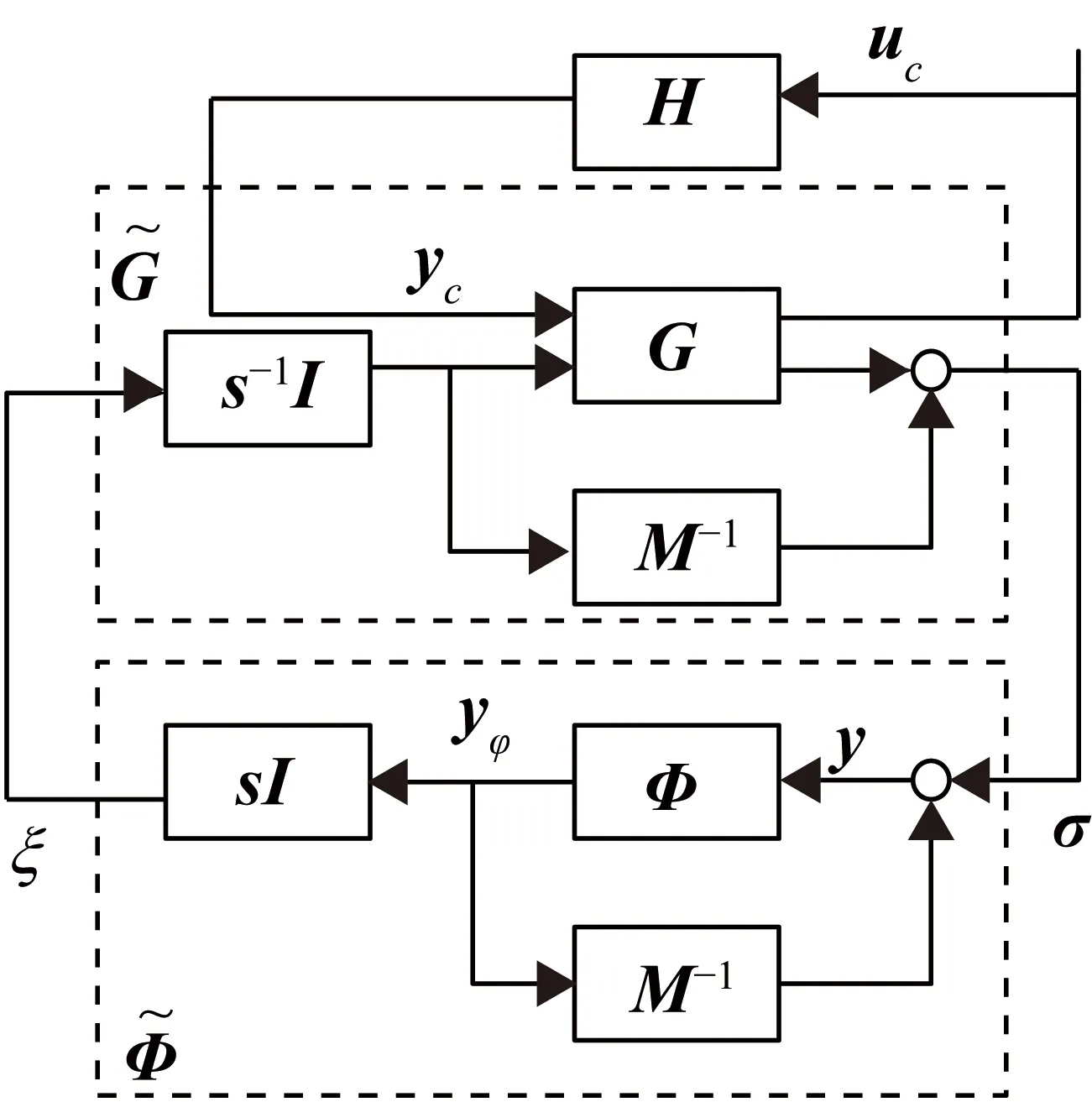
圖4 環(huán)變換后的系統(tǒng)

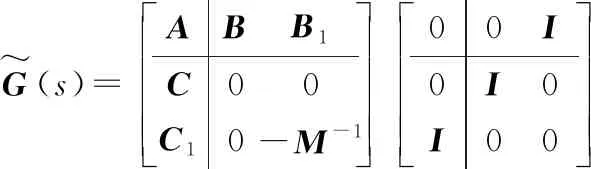
G～(s)=ABB1C00C10-M-1 00I0I0I00

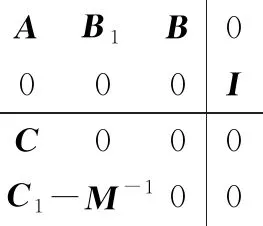
(6)

式中，M為一個嚴格正定的對角陣。圖4中環(huán)變換后系統(tǒng)的狀態(tài)方程為

(7)

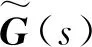
G～(s)=TA～T-1TB～C～T-1D～

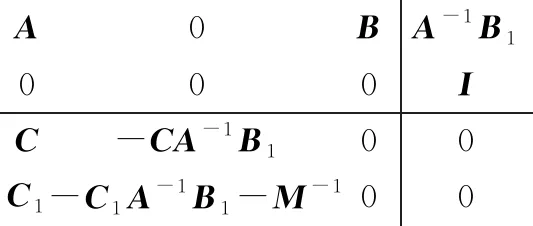
(8)

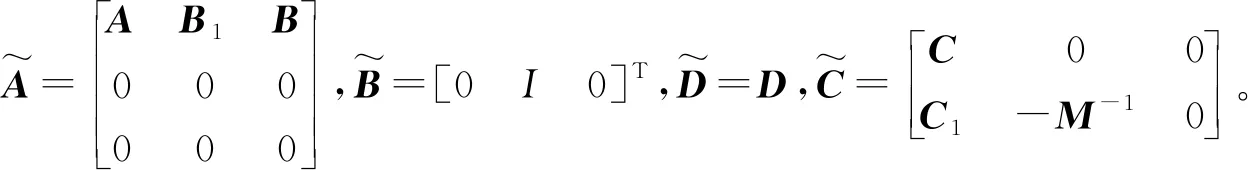
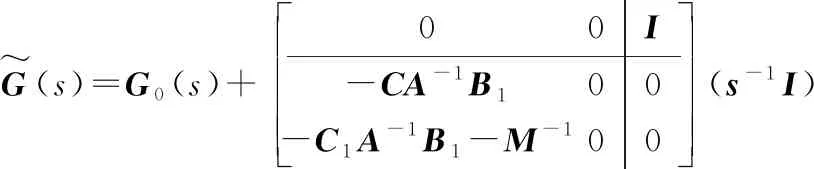
G～(s)=G0(s)+00I-CA-1B100-C1A-1B1-M-100 (s-1I)

(9)

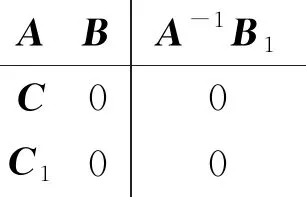
因此定義：

z(t)=x(t)+A-1B1η(t)

(10)

η(t)=ω(t)

(11)

用z和η替換x和ω，則互聯(lián)系統(tǒng)為

(12)

該互聯(lián)系統(tǒng)如圖5所示。

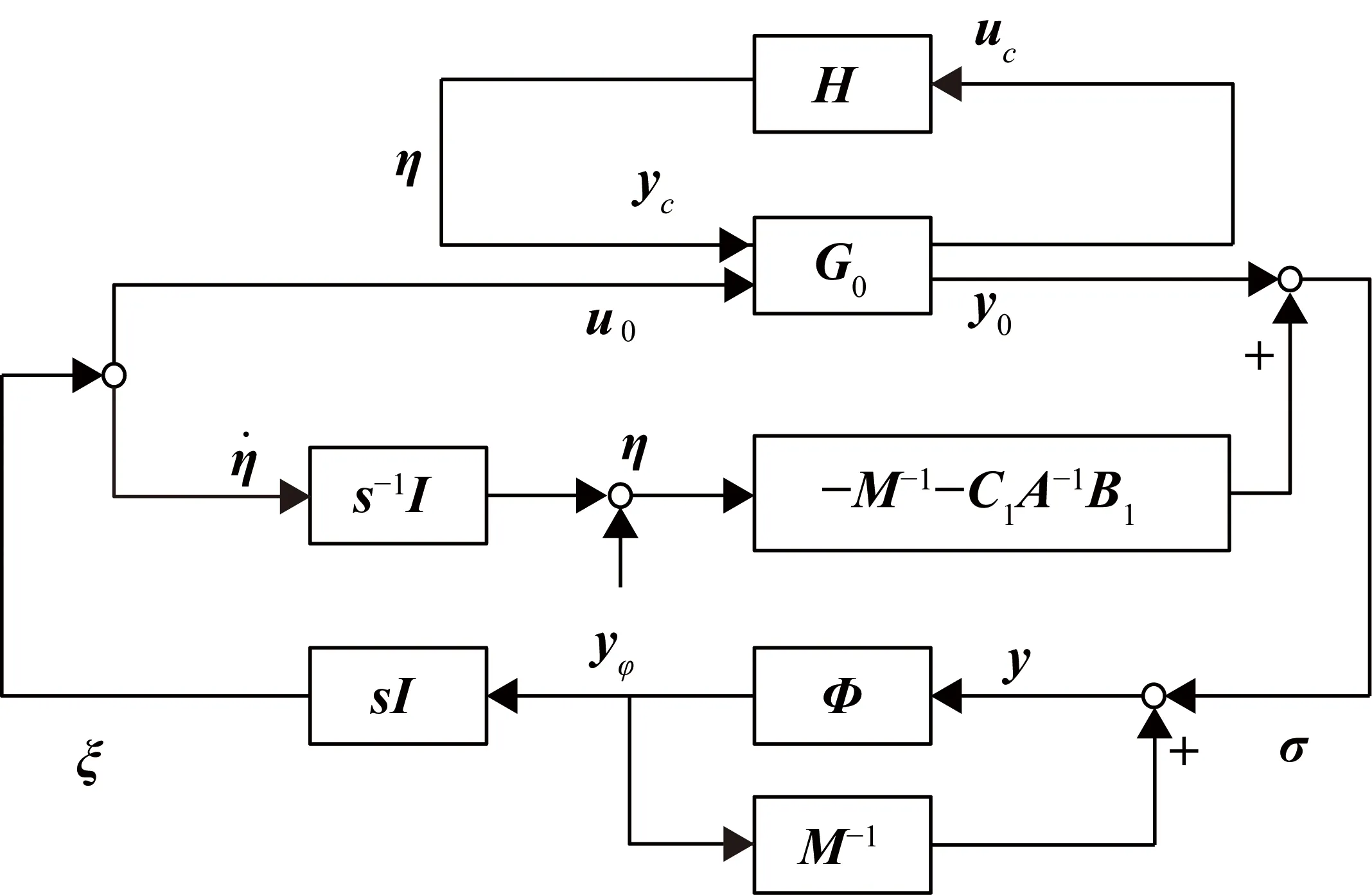
圖5 環(huán)變換、卡爾曼標準分解后的系統(tǒng)

該系統(tǒng)是系統(tǒng)(7)，即圖4分解后的結(jié)果。因此，分析系統(tǒng)(5)的絕對穩(wěn)定性等價于分析系統(tǒng)(7)的絕對穩(wěn)定性，利用卡爾曼標準分解，轉(zhuǎn)化為分析系統(tǒng)(12)的絕對穩(wěn)定性。

2 系統(tǒng)穩(wěn)定性分析

對于由集合Φ的不確定性，負虛的被控對象和嚴格負虛的控制器構(gòu)成的系統(tǒng)，給出了系統(tǒng)絕對穩(wěn)定性的條件和嚴格負虛控制器的DC增益條件。

定理1：考慮集合Φ的不確定性,令M∈Rm×m，是一個由不確定性構(gòu)成對角塊的嚴格正定的對角陣，負虛被控對象G(s)的最小狀態(tài)空間實現(xiàn)為(A,B,C,0)，嚴格負虛控制器H(s)的最小狀態(tài)空間實現(xiàn)為(Ac,Bc,Cc,0)。則系統(tǒng)(5)絕對穩(wěn)定的充分條件是：存在對稱矩陣Y1,Y2>0使得

(13)

(14)

M-1+C1A-1B1>0

(15)

證明：為了證明系統(tǒng)(5)絕對穩(wěn)定，只需證系統(tǒng)(12)絕對穩(wěn)定。令ζ=(z,xc,ξ)T，使用如下的Lur’e-Postnikov李亞普諾夫函數(shù)：

(16)

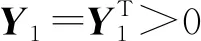
σTξ+ξTσ

=(Az+Byc+A-1B1ξ)TY1z+zTY1(Az+Byc+

ηT(M-1+C1A-1B1)ξ-ηT(C1A-1B1+M-1)Tξ-

ξT(C1A-1B1+M-1)η

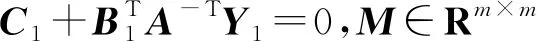
其中,

(17)

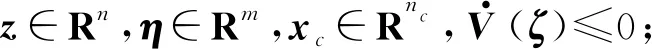
注1：定理1給出了保證系統(tǒng)(5)絕對穩(wěn)定性的充分條件，這和文獻[25]中使用的方法相同，都是環(huán)變換。但是，文獻[25]研究的是負虛系統(tǒng)的絕對穩(wěn)定性。定理1給出的是負虛的被控對象、不確定性和嚴格負虛的控制器的互連作為系統(tǒng)的絕對穩(wěn)定性。

注2：針對非線性系統(tǒng)絕對穩(wěn)定性的研究，其絕對穩(wěn)定性條件建立于線性系統(tǒng)部分已知，非線性部分滿足一定的扇形條件的基礎(chǔ)上，這也是從實際應(yīng)用中得到的重要結(jié)果。因此，定理1的穩(wěn)定性判據(jù)要求系統(tǒng)滿足負虛性質(zhì)和斜率有界符合絕對穩(wěn)定性的判定方法。定理1要求已知負虛被控對象、嚴格負虛控制器和不確定性，但是對于任意滿足條件的負虛和嚴格負虛部分，以及斜率有界這一大類常見的不確定性(如中繼、飽和和量化等)，該定理都適用。

接下來，考慮嚴格負虛控制器部分。如果負虛被控對象和不確定性部分是已知并且滿足一些條件的，那么嚴格負虛控制器只需要滿足一個DC增益條件，就可以使得整個系統(tǒng)穩(wěn)定。

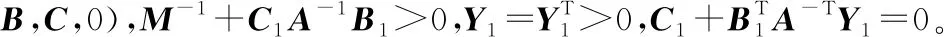
H(0)-1+G(0)≤M-1

(18)

(19)

則系統(tǒng)(5)是絕對穩(wěn)定的。

證明：由定理1的證明，如果T≤0，則系統(tǒng)(5)絕對穩(wěn)定。顯然，由于(19)成立，只需證H(0)-1+G(0)≤M-1，那么(13)成立，則系統(tǒng)(5)是絕對穩(wěn)定的。

(20)

(21)

因此，

(22)

?

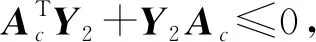
(23)

因為ATY1+Y1A≤0，所以式(23)成立。又因為

(24)

注4：推論給出了控制器的DC增益條件，滿足這一條件的所有嚴格負虛控制器都可以使得該系統(tǒng)絕對穩(wěn)定。也就是說，推論1要求負虛被控對象和不確定性是已知的，但對于廣泛存在的負虛系統(tǒng)，只要當不確定性是斜率有界無記憶的，就可以得到其控制器條件。

3 例子與仿真驗證

本節(jié)給出兩個數(shù)值例子和仿真結(jié)果，用于驗證主要結(jié)論的正確性與有效性。

例1：考慮圖3所示的互聯(lián)系統(tǒng)(5)，不確定性為一維的飽和度：

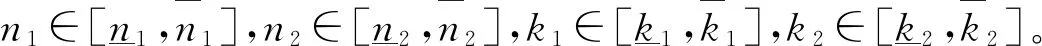
不確定柔性結(jié)構(gòu)運動的常微分方程為

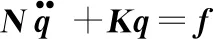
對應(yīng)的狀態(tài)空間方程為

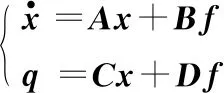
式中，x為系統(tǒng)狀態(tài)；f為力的輸入；q為位移的輸出;系統(tǒng)矩陣為

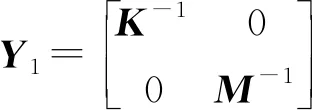
不確定柔性結(jié)構(gòu)如圖6所示。

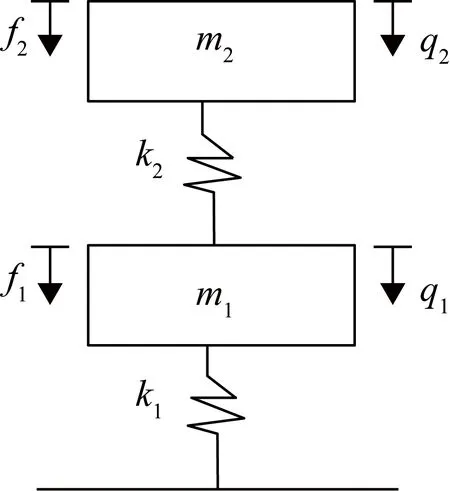
圖6 一個輕阻尼彈簧系統(tǒng)

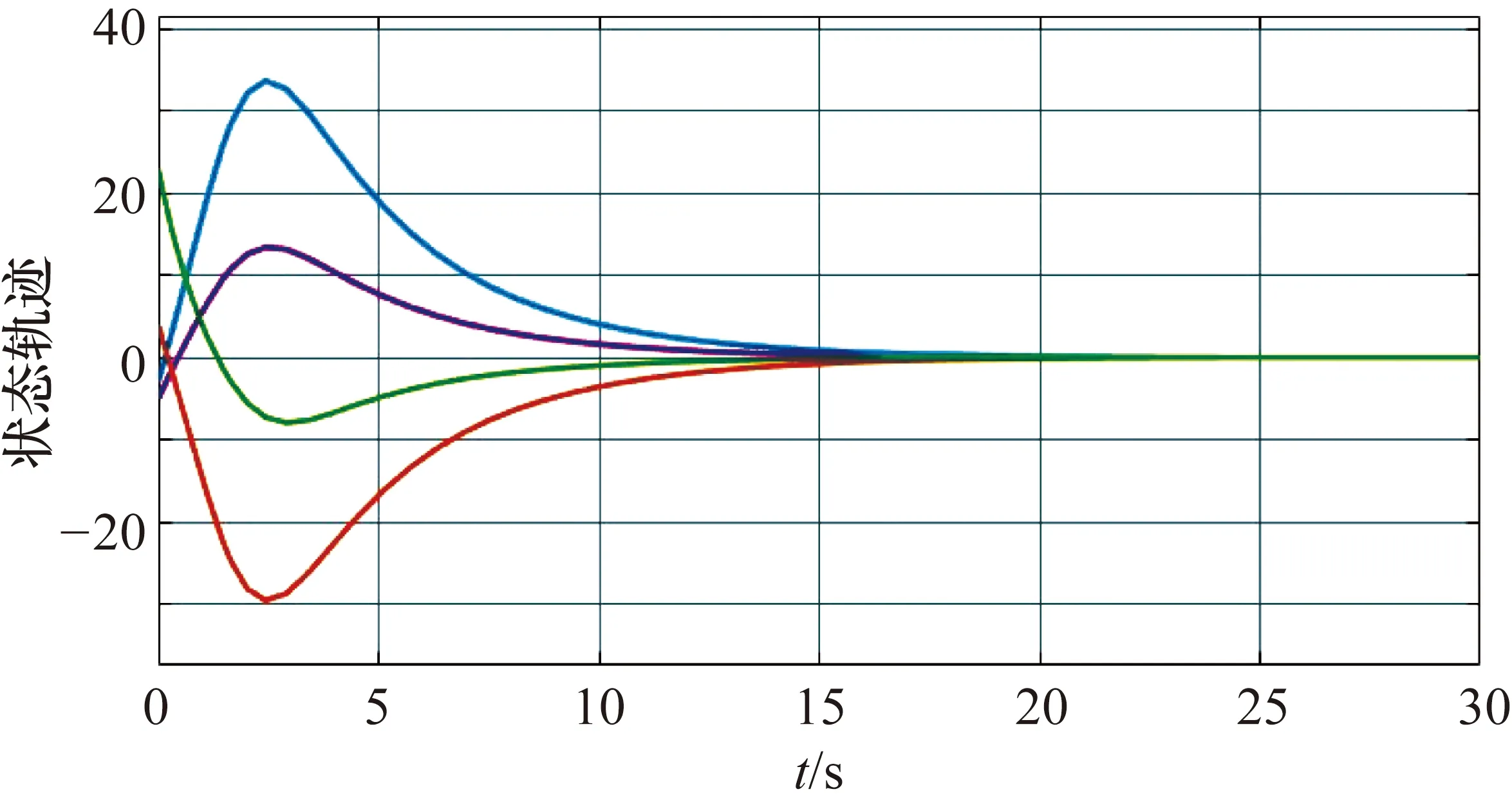
圖7 例1系統(tǒng)狀態(tài)軌跡仿真結(jié)果

例2：為了得到嚴格負虛控制器的條件，負虛被控對象的狀態(tài)空間實現(xiàn)由下面的矩陣給出：

用YALMIP[28]解線性矩陣不等式條件，得到：

考慮Φ1是一個死區(qū)非線性性：

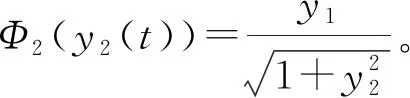
則系統(tǒng)絕對穩(wěn)定，并在仿真結(jié)果圖8中得以驗證，對于任意一個非零的軌跡初值，隨著時間的增長，該系統(tǒng)的狀態(tài)軌跡都會收斂到0。

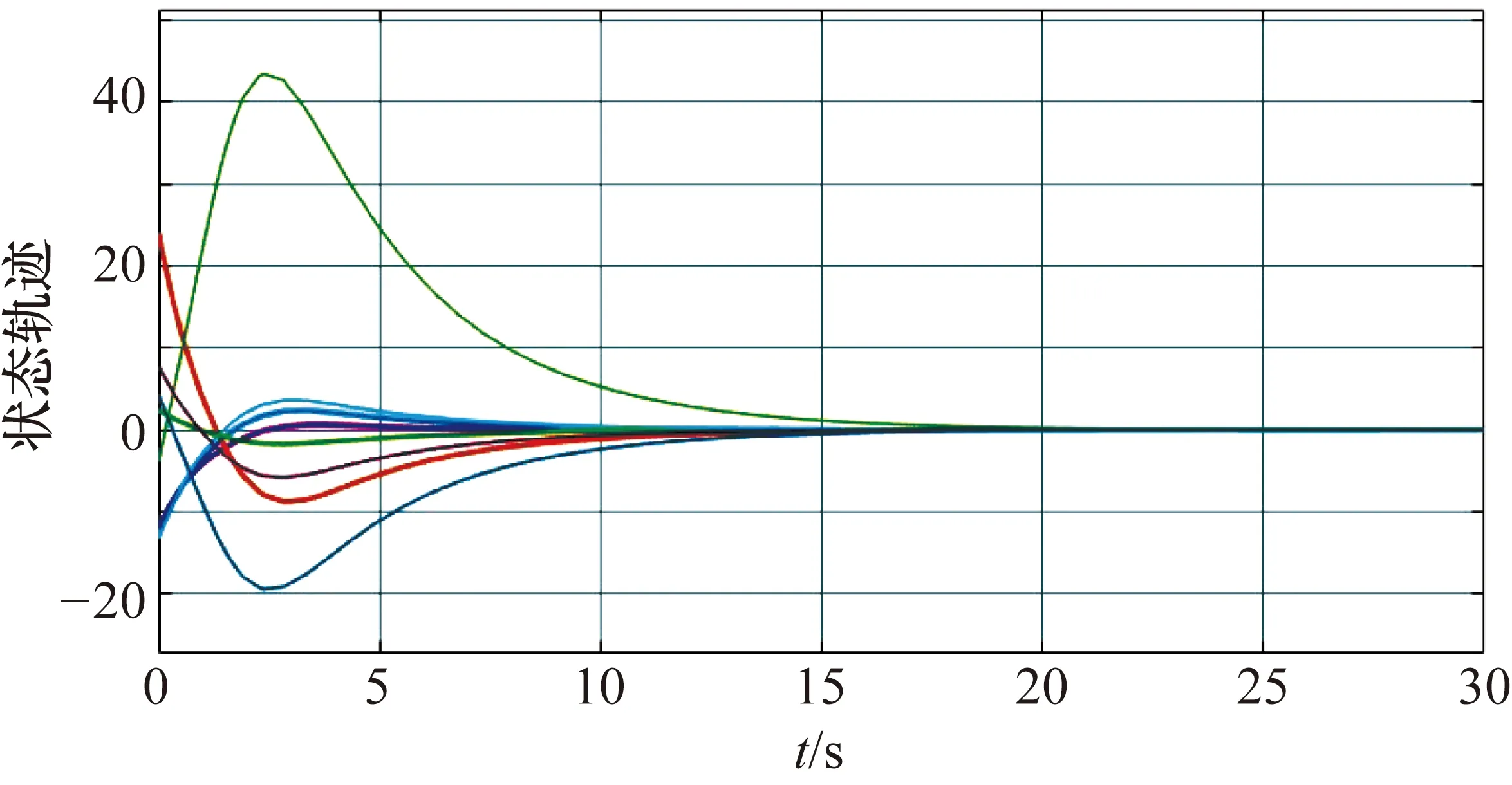
圖8 例2系統(tǒng)狀態(tài)軌跡仿真結(jié)果

4 結(jié)束語

針對帶有不確定性負虛系統(tǒng)互連的絕對穩(wěn)定性研究的不足，利用環(huán)變換等方法研究了負虛系統(tǒng)的絕對穩(wěn)定性。考慮的系統(tǒng)互連為負虛部分、嚴格負虛控制器及不確定性，得出了其絕對穩(wěn)定的條件和控制器的DC增益條件。并在控制器設(shè)計部分對主要理論的結(jié)果進行了拓展，增加了一定的保守性。因此，這樣的嚴格負虛控制器的設(shè)計值得進一步的探索。本文不僅解決了系統(tǒng)的絕對穩(wěn)定性分析，還得到了設(shè)計嚴格負虛控制器的DC增益條件，具有廣泛的應(yīng)用價值。