鋼底板-波形鋼腹板鋼-混組合箱梁剪力滯后效應分析
劉 星,朱世棟,王 巍,王金鳳,李 瑜
1.甘肅彭大高速公路項目管理有限公司,甘肅 平涼 744000
2.甘肅順達路橋建設有限公司,甘肅 蘭州 730000
3.甘肅路橋建設集團有限公司,甘肅 蘭州 730000
波形鋼腹板鋼-混組合箱梁因其具有上部結構自重較輕、箱梁各部受力較為明確、材料利用率高、施工較為便捷的特點,在橋梁工程領域迅速得到應用[1-2]。現有的此類組合結構箱梁主要由波形鋼腹板和頂、底板混凝土結構構成[3-6],但隨著此類結構在工程領域中的不斷應用和探索,新型波形鋼腹板鋼-混組合箱梁逐漸運用于實際工程中。這種結構優化不僅可以繼續有效減輕上部結構的自重,提高橋梁跨越能力,還可以充分利用鋼材抗拉強度高的材料特性,減少正彎矩區底板混凝土受拉開裂的現象[7]。為更加方便、準確地得出此類新型結構的剪力滯后分布規律,文章基于附加撓度法對鋼底板-波形鋼腹板鋼-混組合箱梁剪力滯后效應進行分析與研究。
文章以銀川至昆明國家高速公路(G85)彭陽(甘寧界)至平涼至大橋村(甘陜界)段建設項目涇河特大橋鋼底板-波形鋼腹板鋼-混組合箱梁橋為例,基于能量變分法,以余弦函數為剪力滯后翹曲位移函數,采用附加撓度作為廣義位移來描述鋼底板-波形鋼腹板鋼-混組合箱梁剪力滯后變形狀態,引入軸力自平衡條件與彎矩自平衡條件,推導出集中荷載和均布荷載兩種典型荷載工況作用下鋼底板-波形鋼腹板鋼-混組合箱梁剪力滯后計算公式,并與ANSYS有限元模型進行對比,驗證理論計算方法的正確性,進一步揭示這種新型鋼底板-波形鋼腹板鋼-混組合箱梁的剪力滯后分布狀態。
1 鋼底板-波形鋼腹板鋼-混組合箱梁剪力滯后效應分析
1.1 基本假定
以保證足夠的計算精度為前提,引入“平截面假定”,同時為方便計算,基于等效剛度法(即ASES=ACEC),將鋼底板換算成混凝土底板,得到新的抗彎結構(如圖1所示),并對其進行計算分析。由于波形鋼腹板的褶皺效應,其軸向的彈性模量很小,因此對軸力和彎矩的抵抗作用可忽略不計,即在采用能量變分法求解時可不計入波形鋼腹板的彎曲應變能。
圖1 換算后的鋼底板-波形鋼腹板鋼-混組合箱梁抗彎結構
1.2 附加撓度對剪力滯后變形狀態的描述
當有任意豎向荷載P(z)作用于鋼底板-波形鋼腹板鋼-混組合箱梁并使梁體豎向撓曲變形時,與初等梁理論下的截面變形不同,其截面變形還應包括由剪力滯后效應引起的翹曲變形,如圖2所示。
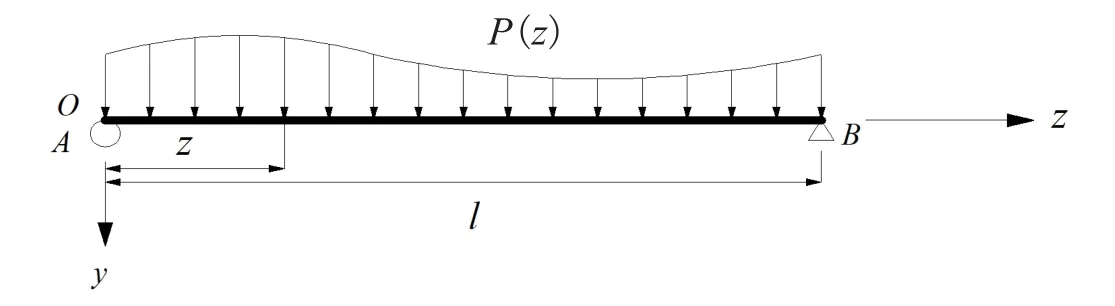
圖2 坐標軸與荷載作用示意圖
文章以剪力滯后效應影響下鋼底板-波形鋼腹板鋼-混組合箱梁豎向抗彎剛度減小、豎向撓度增大這一現象為基礎,以增大的附加撓度作為描述剪力滯后變形的廣義位移,計算橫截面上任意一點的縱向位移u(x,y,z):
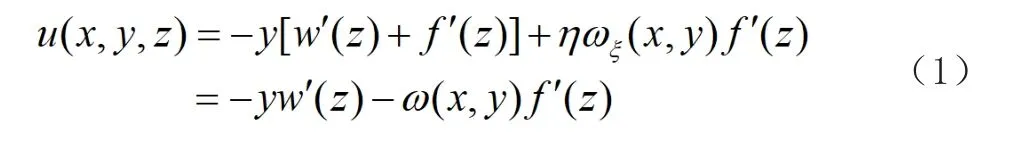
式中:η為引入的彎矩自平衡修正系數;f(z)為剪力滯后效應引起的附加撓度;w(z)為初等梁理論引起的撓度;ωζ(x,y)為剪力滯后翹曲函數;ω(x,y)為相應于附加撓曲轉角的廣義位移函數,即。
基于胡克定律,可得組合箱梁任意截面一點處正應力的表達式如下:
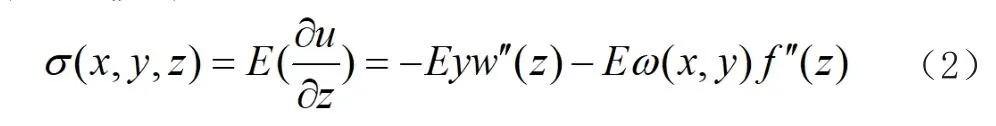
式中:-Eyw"(z)為基于初等梁理論的正應力表達式;-Eω(x,y)f"(z)為基于剪力滯后效應的翹曲應力表達式。可得:

在豎向荷載作用下組合箱梁任一截面上翹曲應力應滿足相應自平衡條件,由此可得:

由式(2)可知,鋼底板-波形鋼腹板鋼-混組合箱梁任意點處的總正應力為剪力滯后效應引起的翹曲正應力與初等梁理論相應的正應力之和,即:

1.3 控制微分方程與初參數解
文章將鋼底板-波形鋼腹板鋼-混組合箱梁的剪力滯后變形形態與初等梁變形狀態分離開來研究,受如圖1所示的任意豎向荷載P(z)作用的鋼底板-波形鋼腹板鋼-混組合箱梁,其總勢能的一階變分如下:


式中:A、B、C、D為鋼底板-波形鋼腹板鋼-混組合箱梁兩段相應邊界條件對應的常數。
對于跨內受任一集中荷載P的鋼底板-波形鋼腹板鋼-混組合箱梁(如圖3所示),可得相應的附加撓度與廣義力矩的計算式如下:
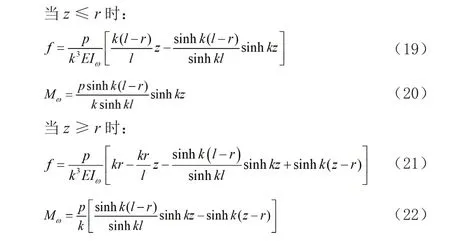
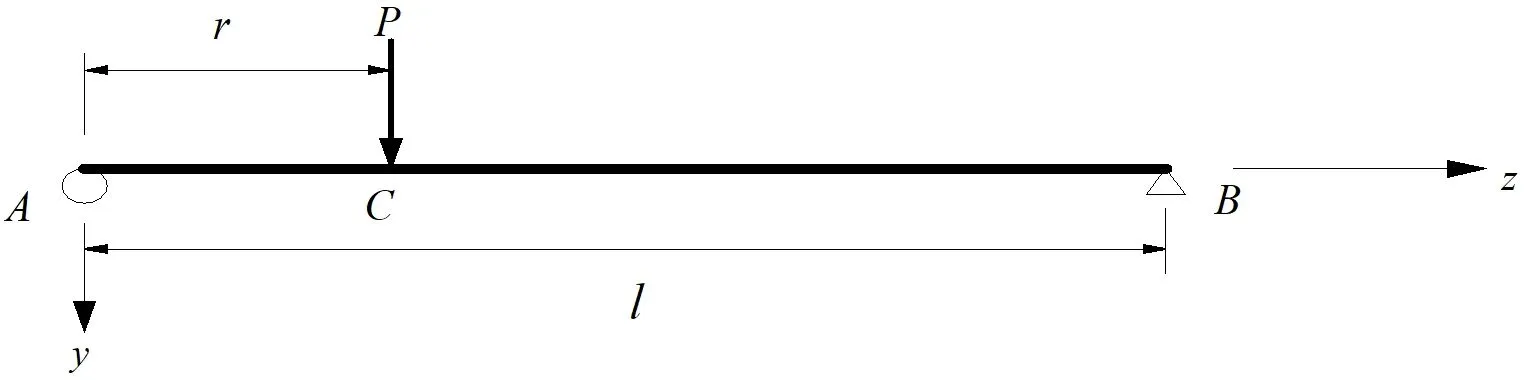
圖3 簡支梁任一截面受豎向集中荷載P作用
對于跨內受任一滿跨均布荷載q的鋼底板-波形鋼腹板鋼-混組合箱梁(如圖4所示),可得梁的附加撓度與廣義力矩的計算式如下:
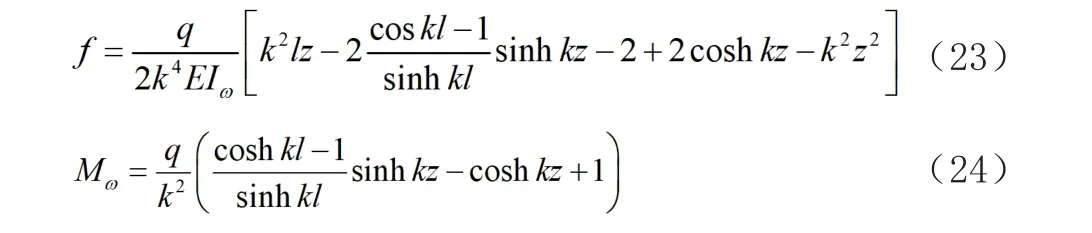
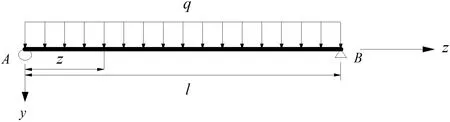
圖4 簡支梁任一截面受豎向均布荷載q作用
1.4 截面幾何特性計算
文章選取余弦函數為鋼底板-波形鋼腹板組合箱梁翹曲位移函數,如圖5所示。由此可得如下形式的翹曲位移函數:
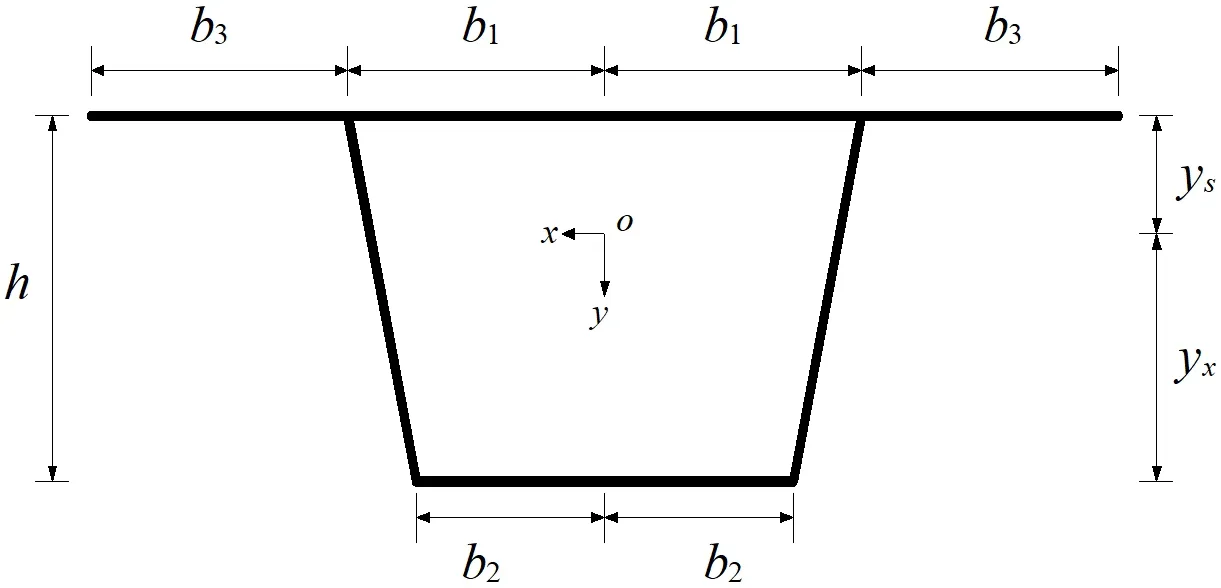
圖5 梯形橫截面箱梁

式中:α為懸臂板影響的修正系數,即α=(b3/b1)2;β為底板影響的修正系數,即β=(b2/b1)2(yx/ys);d為軸力自平衡條件引起的附加軸向位移,d需滿足:

由式(25)與式(26)可得d的表達式如下:
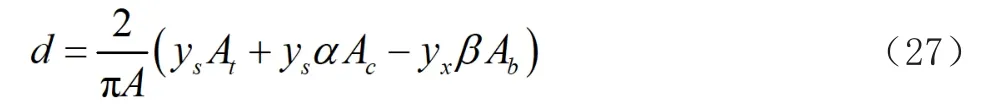
式中:A為組合箱梁橫截面面積之和;At為組合箱梁頂板面積;Ac為組合箱梁懸臂板面積;Ab為組合箱梁底板面積。
由剪力滯后翹曲位移函數可推導出其他截面幾何特性表達式:
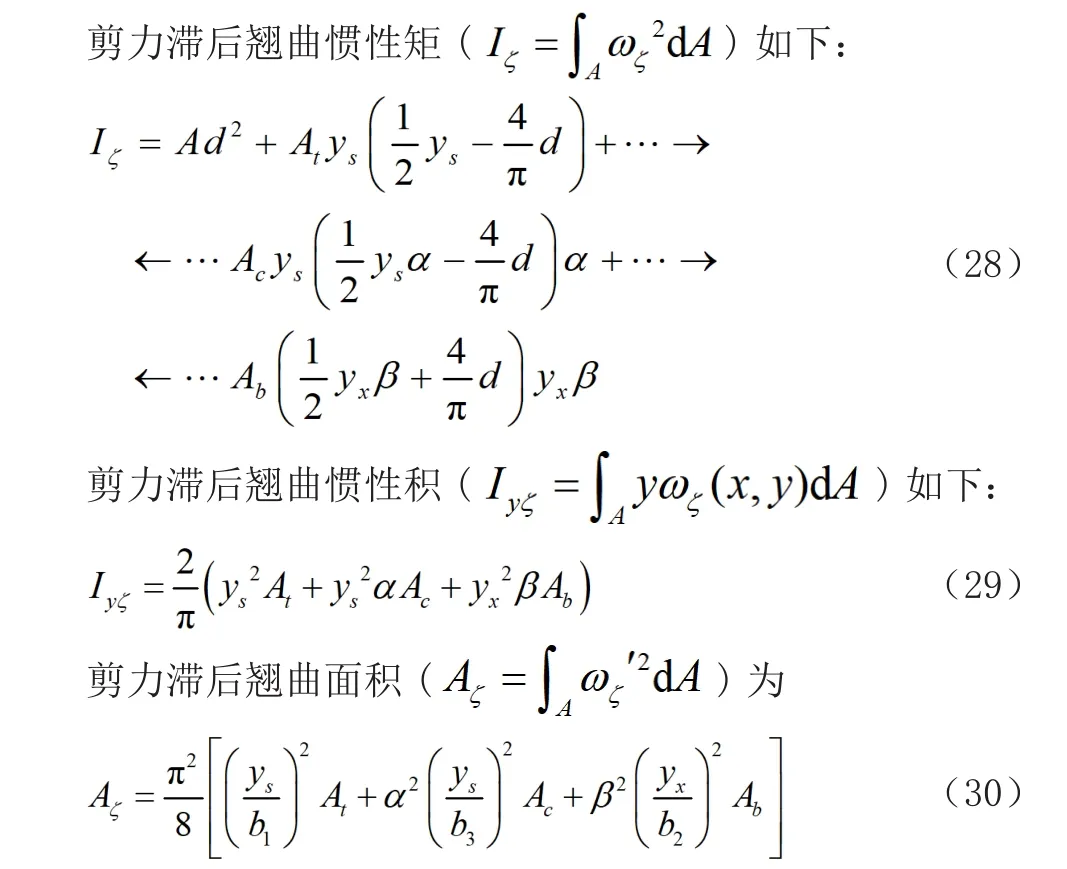
2 算例分析
2.1 有限元模型建立
此小節以銀川至昆明國家高速公路(G85)彭陽(甘寧界)至平涼至大橋村(甘陜界)段建設項目涇河特大橋鋼底板-波形鋼腹板鋼-混組合小箱梁為算例,對理論方法進行驗證。該橋全長50m,計算跨徑48.92m,橫截面尺寸及橫截面計算點布置如圖6所示。
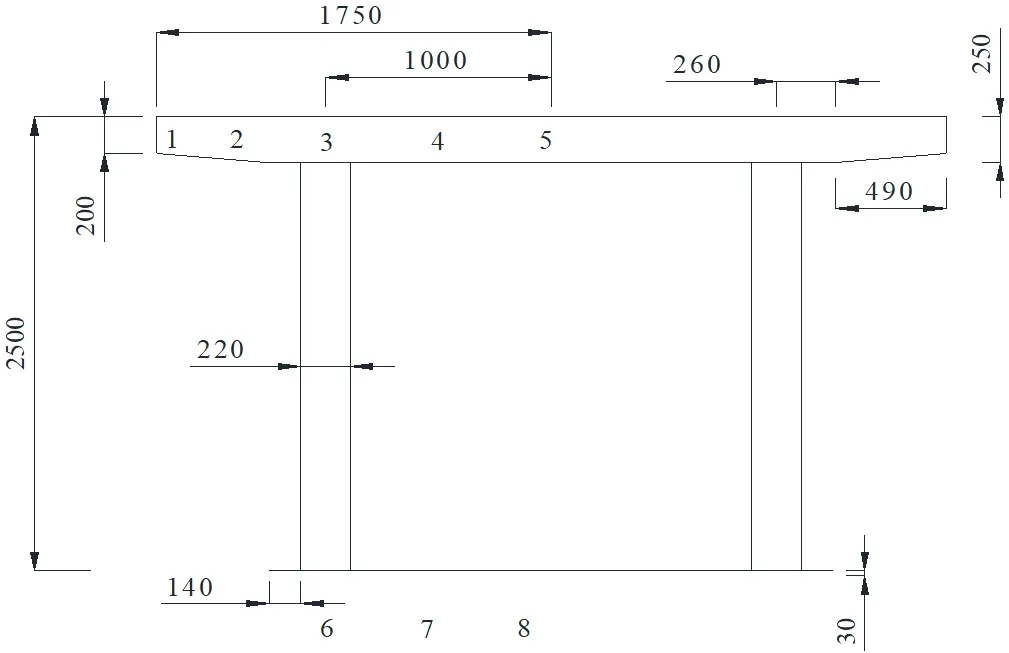
圖6 鋼底板-波形鋼腹板鋼-混組合箱梁橫截面尺寸(單位:mm)
相應的頂板、懸臂板采用C50微膨脹混凝土,鋼底板采用Q370qD鋼材,波形鋼腹板采用Q345qD鋼材。各種材料的主要材料特性值如表1所示。
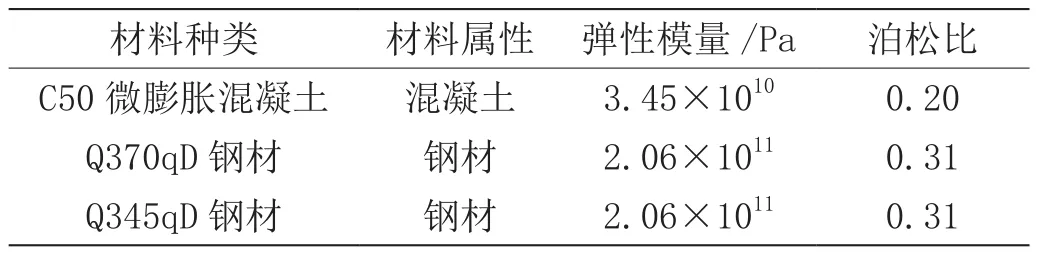
表1 各種材料的主要材料特性值
計算時,對鋼底板-波形鋼腹板鋼-混組合箱梁跨中施加兩種的荷載,如圖7、圖8所示。
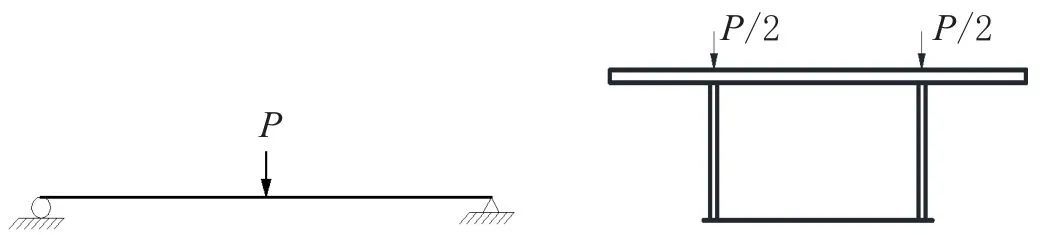
圖7 鋼底板-波形鋼腹板鋼-混組合箱梁受集中荷載作用示意圖
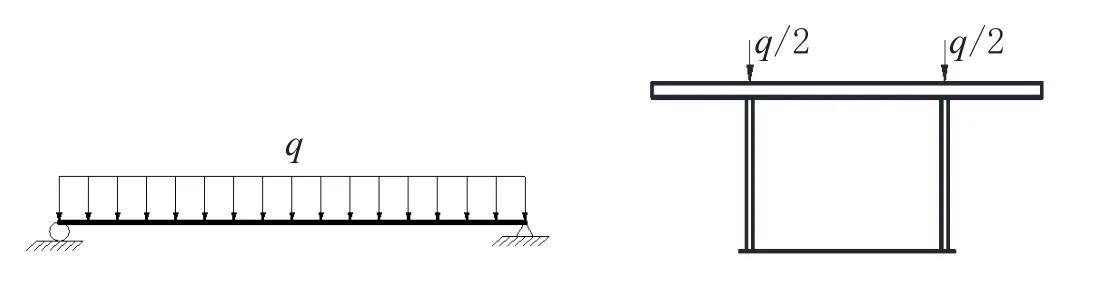
圖8 鋼底板-波形鋼腹板鋼-混組合箱梁受均布荷載作用示意圖
在建模過程中,采用Solid 45單元來模擬頂板及懸臂板混凝土結構,采用Shell 63單元來模擬波形鋼腹板及鋼底板結構,各板件結構采用共節點方式進行連接,從而使其協調一致工作,有限元模型如圖9所示。

圖9 鋼底板-波形鋼腹板鋼-混組合箱梁ANSYS有限元模型
2.2 計算結果對比分析
文章以跨中截面作為計算截面來分析鋼底板-波形鋼腹板鋼-混組合箱梁簡支狀態下的剪力滯后效應的橫向分布,分析時施加如圖7、圖8所示的集中荷載及均布荷載,得出相應的理論計算結果和有限元模擬計算值,如表2、表3所示。
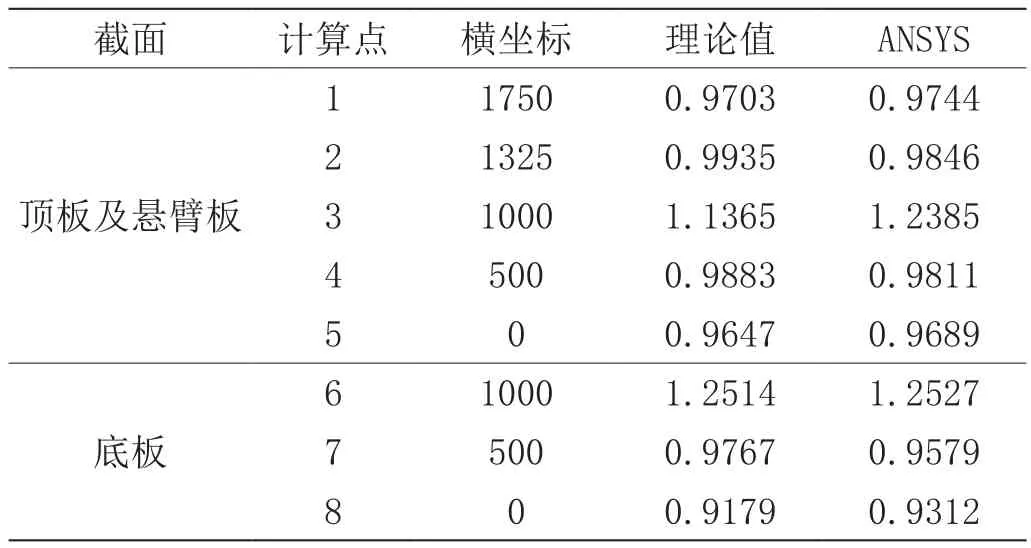
表2 鋼底板-波形鋼腹板鋼-混組合簡支箱梁集中荷載作用下跨中計算截面剪力滯后系數對比
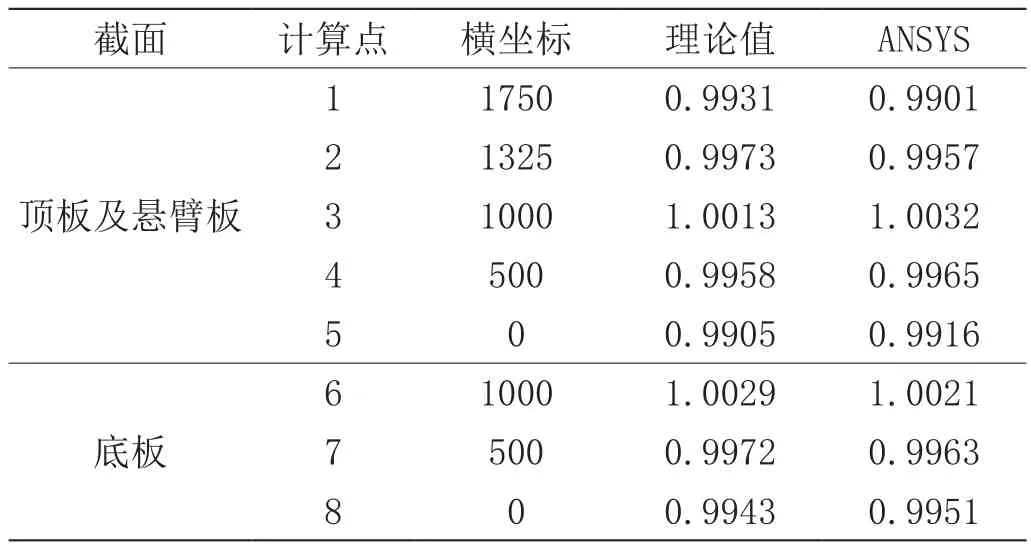
表3 鋼底板-波形鋼腹板鋼-混組合簡支箱梁均布荷載作用下跨中計算截面剪力滯后系數對比
由表2、表3可知,受相應跨中集中荷載和滿跨均布荷載作用時,運用附加撓度法所得的簡支鋼底板-波形鋼腹板鋼-混組合箱梁跨中截面各個計算點的剪力滯后系數與ANSYS有限元模型所得的計算結果較為吻合,最大誤差絕對值僅為8.23%。同時,由計算結果可以很明顯地看出,剪力滯后系數橫向分布規律是由頂板中心和懸臂板端部的負剪力滯后現象向波形鋼腹板與頂板、懸臂板相交處逐步過渡到正剪力滯后現象,并且鋼底板與混凝土頂板的剪力滯后系數分布規律相同,這證明了文章所述方法的正確性。
3 結束語
文章結合鋼底板-波形鋼腹板鋼-混組合箱梁的結構特點,利用附加撓度法對銀川至昆明國家高速公路(G85)彭陽(甘寧界)至平涼至大橋村(甘陜界)段建設項目涇河特大橋鋼底板-波形鋼腹板鋼-混組合箱梁剪力滯后效應進行研究,得到以下結論:
(1)以等效剛度法為基礎,將鋼底板換算成混凝土底板,得到新的鋼底板-波形鋼腹板鋼-混組合箱梁抗彎結構模型,利用考慮自平衡條件后的附加撓度法在兩種荷載工況下計算出的鋼底板-波形鋼腹板鋼-混組合箱梁各點的剪力滯后系數與ANSYS有限元模型計算結果吻合良好,證明了文章所述方法的正確性。并且由計算結果可知鋼底板-波形鋼腹板鋼-混組合箱梁存在明顯的剪力滯后現象,在此類橋梁設計及施工中為保證結構的安全與穩定,應充分考慮該現象對橋梁結構的影響。
(2)由計算結果可以看出,在兩種荷載工況下,頂板、懸臂板及底板隨著橫坐標發生變化,與此同時鋼底板-波形鋼腹板鋼-混組合箱梁橫截面上會出現正、負剪力滯后效應變化現象,由此揭示了剪力滯后效應在鋼底板-波形鋼腹板鋼-混組合箱梁上的橫向分布情況。

