微型樁-連梁組合結構的邊坡加固機理與內力計算方法

馬華 雷國平 蘇棟，3 李華林 吳澤雄 楊偉鴻 張院生

1.鐵科院（深圳）研究設計院有限公司，廣東 深圳 518060；2.深圳大學土木與交通工程學院，廣東 深圳 518060；3.深圳大學未來地下城市研究院，廣東 深圳 518060

抗滑樁是邊坡加固的常用手段，微型抗滑樁（樁徑100～300 mm，長徑比大于30）作為典型的柔性抗滑樁，因其施工快捷、對場地適應性強、造價低等優點，近年來被廣泛應用于中小型滑坡的治理中。國內外的研究一定程度上揭示了該結構的受力特性，但是對滑坡土體位移作用下微型樁縱橫彎曲變形下的受力機理、樁頂連梁的影響、微型樁的臨界嵌固長度等方面的研究不足，針對該結構的內力計算方法也未能合理考慮其受力特性，這在一定程度上阻礙了該結構的應用與發展。本文對國內外的相關研究進行總結，分析該結構對邊坡的加固機理，并對其影響因素進行探討，提出下一步研究的方向。

1 微型樁組合結構常見形式

微型抗滑樁組合結構的工程應用有多種形式，根據樁的排列角度分為兩種類型。

1）傾斜交叉型。該類型在國外的應用較多，采用傾斜微型樁以非平行的方式排列，并在樁頂設置頂梁。根據滑坡大小可采用A 字形（A?frame）結構或網狀結構，如圖1（a）、圖1（b）所示，在同一個滑坡中也可設置多級該類結構。

2）多排平行型。國內主要采用此類結構，一般將3 排及以上微型樁以平行或近似平行的方式排列，根據設置位置可分為坡面加固型和平臺加固型［1］，如圖1（c）、圖1（d）所示。坡面加固型的微型樁可垂直于坡面或豎向設置，樁頂采用連梁連接。平臺加固型則在坡面較平緩處設置微型樁群，樁頂采用連梁或頂板進行加固，處于邊緣的微型樁也常采用稍微傾斜的設置。本文主要以此類多排微型樁-連梁組合結構為研究對象進行總結和分析。

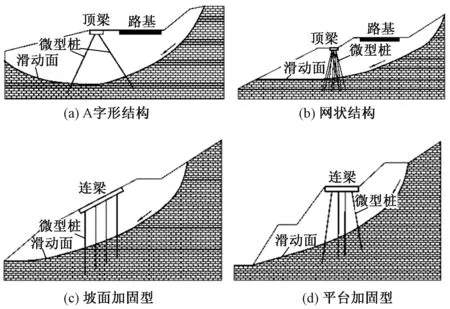
圖1 常見的微型抗滑樁組合結構

2 微型樁-連梁組合結構加固機理

圖2 微型抗滑樁的變形特征試驗

微型抗滑樁組合結構的抗滑作用來源于四個方面：①微型樁在滑面處提供較大的抗剪力［1］。②樁與土形成抗滑體，共同抵抗滑坡推力［1］。③微型樁因受剪切變形在樁與滑面相交處產生兩個塑性鉸（圖2），導致該處樁身傾角增大，樁由受剪變為受拉，充分發揮了加筋材料的受拉優勢［1，6］。④微型樁在滑面處的彎曲變形導致樁身產生縱向位移，在樁表面產生摩擦力，該力傳至土體中增加了滑面處的法向力，間接產生抗滑力［7］。

由此可知，微型樁在滑坡位移作用下同時受到橫向力和縱向力的影響。根據梁結構理論［8］，同時受軸向力P和橫向力Q作用的梁在彎曲變形較大時，因軸向力產生的二次彎矩不可忽略，該梁的變形屬于縱橫彎曲變形，如圖3（a）所示，其中δ為梁的最大撓度。而對于微型樁，在滑坡橫向推力作用下產生彎曲變形，同時產生軸向收縮位移，并在樁土界面摩擦力的作用下產生軸向力，如圖3（b）所示，其中p為樁土橫向作用力；t為軸向摩阻力；δlat為樁土最大橫向相對位移；δaxial為樁土最大軸向相對位移。由于微型樁的彎曲剛度較小，軸力導致的彎矩變化和變形不可忽略，微型樁的變形也屬于縱橫彎曲變形，其加固機理尚待進一步研究。

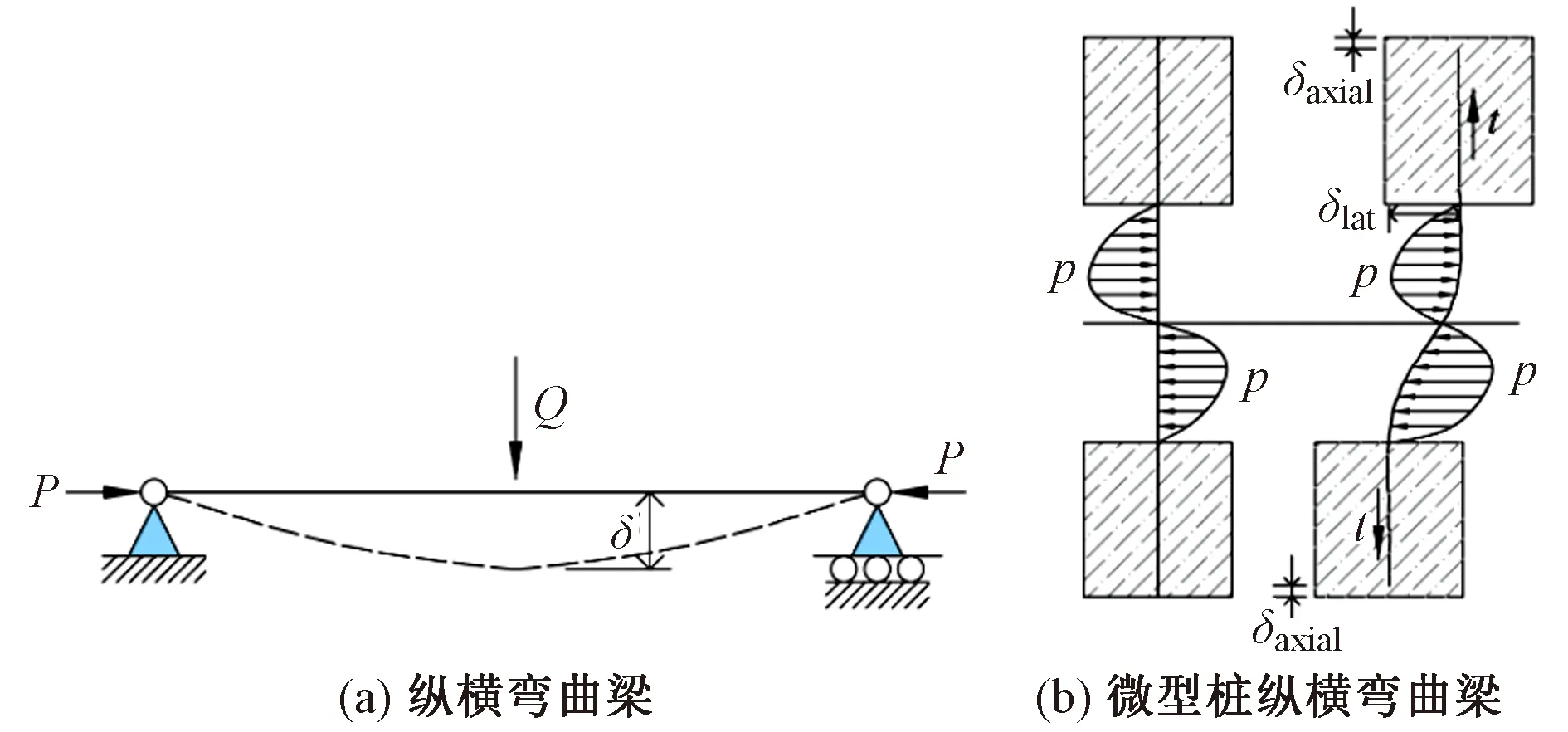
圖3 梁和微型抗滑樁的縱橫彎曲變形示意

3 微型樁-連梁組合結構加固的影響因素分析

3.1 微型樁與滑面法向的夾角

微型樁與滑面法向的夾角θ決定了滑坡土體運動對微型樁受力的影響。國外對A 字形微型樁的現場試驗［9-10］和模型試驗［11］顯示，處于A 字形結構中兩個不同角度的樁在受力上有較大的區別。如圖4 所示，對于處于右側的微型樁（θ＜0），土體位移有一個沿樁身縱向向上的分量，在樁表面產生沿縱向向上的摩擦力而導致微型樁受拉，而對于左側的微型樁（θ＞0）則相反產生了軸向壓力，微型樁在滑面處的軸力和剪力共同起抗滑作用。圖4中F為滑坡下滑力；α為滑面傾角；u為土體位移；un、uf分別為土體相對樁的橫向和軸向位移分量；V為樁在滑面處的剪力。

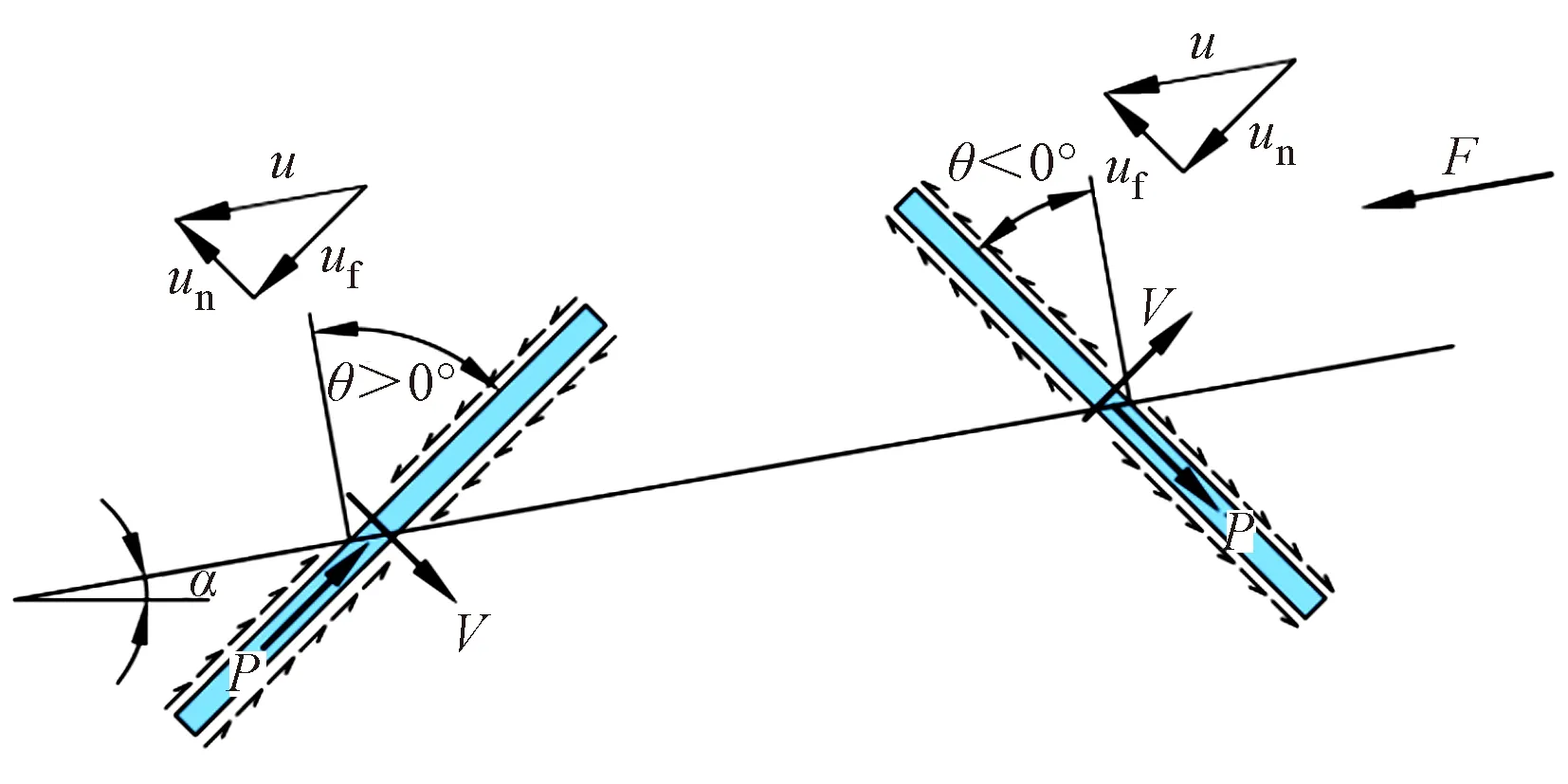
圖4 傾斜微型抗滑樁表面摩擦力分布

Loehr 等［7］根據滑面處微型樁的簡化變形模式推導了其抗滑力的簡化計算方法，同時也通過彈塑性p?y（其中y為樁土橫向相對位移）和t?z（其中z為樁土縱向相對位移）模型分別對微型樁的彎矩和軸力進行了分析，得到了與試驗相近的結果。這種直接將滑坡位移分解的分析方法比較適用于θ較大的情況（即樁所受縱向土體位移較大），而對于國內常見的微型樁與滑動面近乎垂直的情況（即樁所受縱向土體位移較小）可能會產生較大的誤差。

如圖5所示的豎直微型樁，根據位移分解分析，該微型樁軸向應受壓力，然而由于滑面處的彎曲變形導致樁發生了縱向收縮位移，有可能出現樁的軸向位移大于土體縱向位移分量的情況，從而改變了樁所受縱向摩擦力的方向，導致樁身受拉。這種豎直微型樁受

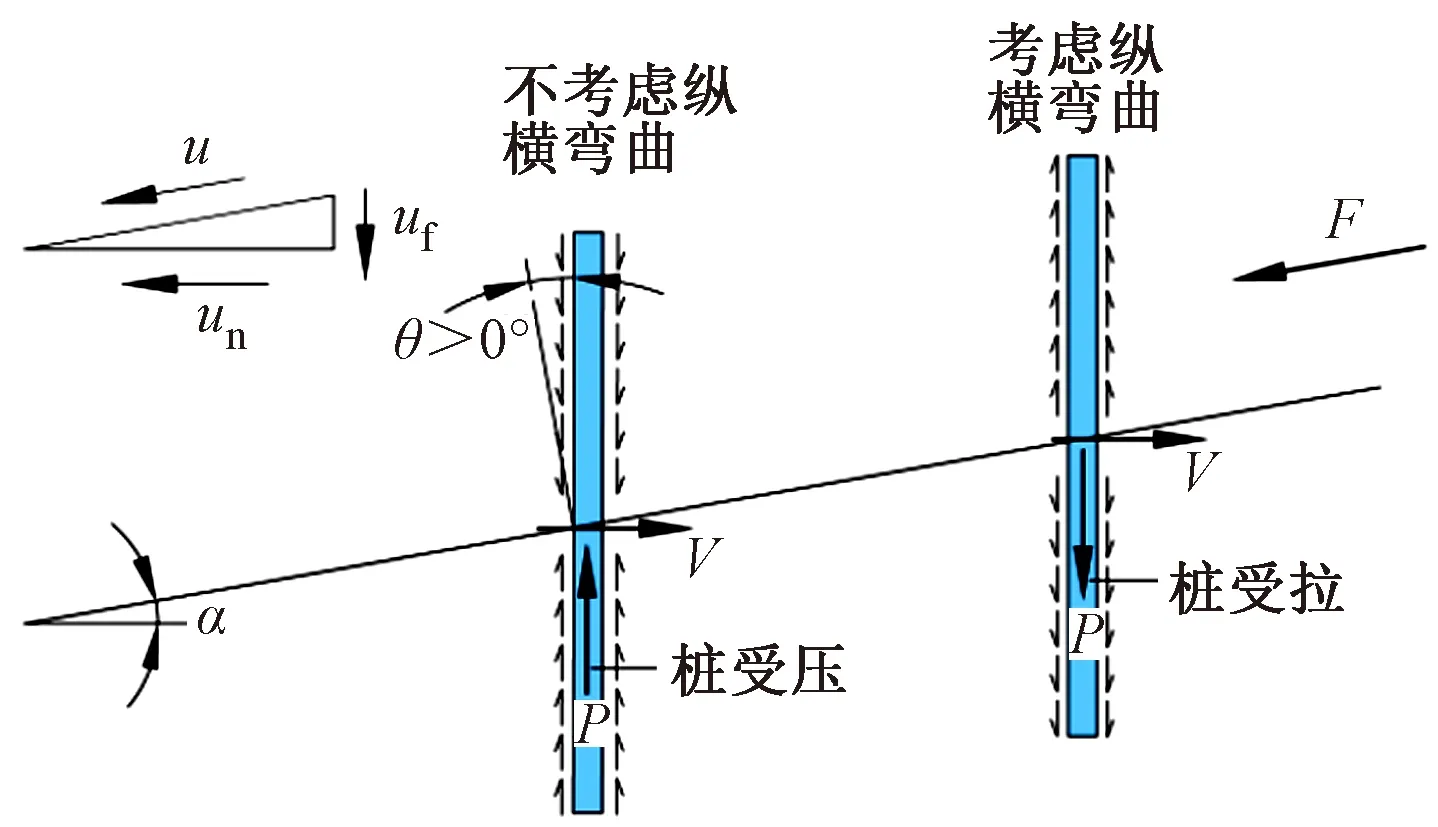
圖5 垂直微型抗滑樁表面摩擦力分布

拉的現象已被國內多個現場監測和室內試驗所證實［1，12-14］，因此有必要進行微型樁縱橫彎曲變形下的受力機理研究，分析不同滑坡位移角度對微型樁受力的影響。

通過加強水土保持措施設計，合理安排施工進度與工序，抓緊落實土地整治及植被恢復，減少地表裸露時間，以減少施工過程中因降水和風等水土流失影響因素產生的水土流失。

3.2 樁頂約束

微型抗滑樁一般采用連梁或承臺對樁頂進行約束，模型試驗及數值仿真研究［11，15-16］表明，樁頂約束能使排樁與土體共同發揮抗滑作用，有效提高土質邊坡中微型樁的加固效果，其中縱向連梁（沿滑坡方向）的作用明顯高于橫向連梁（垂直滑坡方向）。向波等［17］通過離心試驗發現，在樁頂連梁作用下邊坡安全系數提高了38.3%。樁頂約束的影響也與滑體性質有關，連梁對整體性較好的滑體作用較小，而對整體性較差的松散土體影響很大［1］。

微型抗滑樁組合結構中，一般靠近滑坡后緣的一排樁受力最大，其他排樁的受力依次減小［18］，受力大小的不同導致各排樁樁頂位移的差異。如圖6（a）所示，在沒有連梁的作用下，各排樁的變形存在大小差異但模式相近。而在有連梁的情況下，如圖6（b）所示，樁頂的水平位移差異受到約束，連梁后緣出現向上的位移而前緣出現向下的位移［1，19］，從而起到力的傳導作用（包括水平力和軸向力），若樁頂和連梁為固定連接，則還會產生樁頂彎矩。如圖6（c）所示，水平力的傳導導致連梁軸向受壓，后緣樁的樁頂出現了較大的負向剪力而前緣出現正剪力［20］，軸向力的傳遞主要導致前緣的樁受壓，并加強了后緣樁的受拉。王洋等［13］通過對3×3 微型抗滑樁-頂板組合結構的原位試驗發現，后緣樁的最大拉力出現在樁體下部，中間排樁的最大拉力出現在中上部，而前緣樁的最大壓力出現在樁體上部，并且隨著推力的增大，受壓區不斷增大，體現了樁頂約束對軸力的傳導過程。

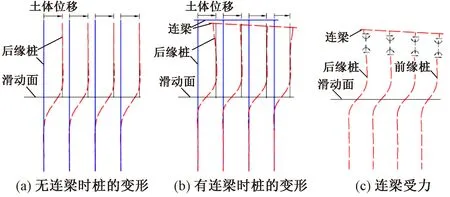
圖6 連梁對微型樁作用示意

目前對于樁頂約束的影響主要以定性研究或以其對各排樁所受滑坡推力比例的定量研究［15-16］為主，連梁的存在一定程度上抑制了后緣樁的縱橫彎曲變形而加強了前緣樁的變形，使組合結構的加固機理更為復雜，需要進一步的研究。

3.3 嵌固長度

微型樁嵌入滑床的長度直接影響著微型樁的抗滑能力，嵌固段除了滿足微型樁水平抗力的需求外還要滿足抗拔和抗壓承載力的需求［21］。當嵌固長度過短時，滑面以下土體達到水平抗力極限，微型樁以整體隨滑坡移動的剛性運動為主［22］［圖7（a）］。當嵌固長度足夠時，則需考慮微型樁抗彎強度是否滿足要求［圖7（b）］。Viggiani［23］研究了剛性抗滑樁最大彎矩和樁嵌固比λ（嵌固長度與受力段長度的比值）的關系，并得出了發生橫向剛性運行的λ臨界值。Lei 等［24］對柔性樁的λ臨界值和最大彎矩進行了研究，是對微型樁嵌固長度的初步分析，但是該研究尚未考慮微型樁縱橫彎曲的特性和樁頂連梁的影響。

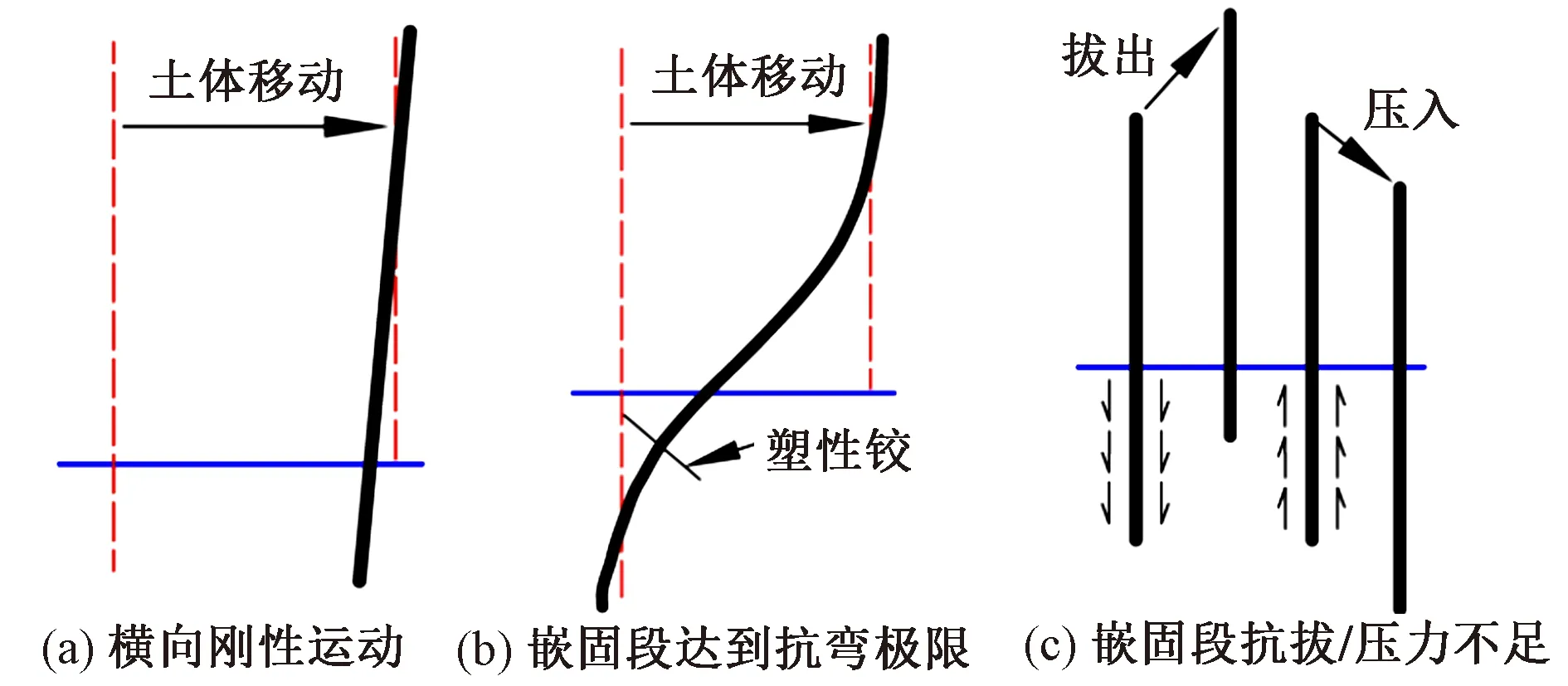
圖7 微型樁嵌固端作用示意

當微型樁嵌固長度滿足橫向受力的要求時，還應進行軸向抗拔或抗壓驗算［圖7（c）］。微型樁在滑動面處的極限拉∕壓力（Pult）為

式中：αf1是滑體中的樁土界面摩擦因數；L1是微型樁在滑體中的長度；d是樁徑。

微型樁滿足抗拔或抗壓穩定需求的臨界深度L2crit為

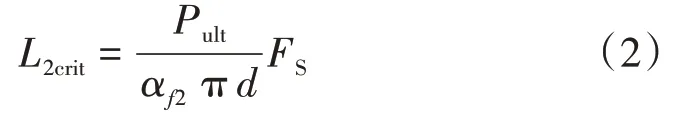
式中：αf2是嵌固段的樁土界面摩擦因數；FS是穩定性系數。

以上計算方法的缺點是沒有考慮微型樁變形過程中摩擦力的真實分布以及連梁導致的微型樁軸向力的變化。

由于對微型樁-連梁組合結構的受力計算缺乏合理的定量分析模型，目前對微型樁的臨界嵌固長度尚未達成統一認識。GB∕T 38509—2020《滑坡防治設計規范》建議嵌固長度不大于1∕3 總樁長，而孫書偉等［25］通過對微型樁加固土質邊坡的數值模擬研究建議最優錨固長度取自由段長度的1.5～2.0倍。因此，有必要在微型樁受力機理分析和連梁作用研究的基礎上探討微型樁的臨界嵌固長度，為微型樁樁長的設計提供理論支持。

3.4 微型樁間距

微型樁群的平面排列方式一般有行列式排列和品字形排列。在相同的樁間距的情況下，品字形排列的微型樁群承載力更高［14，26］，也是GB∕T 38509—2020推薦的排列方式。微型樁間距根據與滑坡方向的關系包括橫向間距（垂直滑坡方向）和排間距（平行滑坡方向）。

橫向間距的影響與傳統大直徑抗滑樁間距類似。當橫向間距小于臨界間距時，在滑坡推力作用下，樁間產生土拱效應而抵抗樁間土的水平運動，單樁抗滑力隨間距的增加而增大［27-30］。對于大直徑樁，該臨界值約為4倍樁徑［27］。對于微型樁，Bruce等［31］認為當樁間距為7～8倍樁徑時可忽略群樁效應；何暉［18］認為樁間距為8～10 倍樁徑時土拱效應最為明顯；向波等［17］的離心試驗顯示，樁間距與邊坡安全系數呈冪函數關系，并建議樁間距控制在6～12倍樁徑。

杜衍慶［32］通過有限元計算，發現排間距對微型抗滑樁承載力的影響大于橫向間距，排間距過小會導致微型樁整體抗彎剛度降低，排間距過大則會造成微型樁群工作性能降低，后緣樁承擔較大的滑坡推力，而前緣樁不能有效發揮作用，并建議最佳排間距為5 倍樁徑。朱寶龍等［5］通過離心試驗也發現，排距越大后緣微型樁承受的土壓力越大。何暉［18］的試驗顯示，排間距為5～10 倍樁徑時，各排樁分擔的滑坡推力比較均勻，工作性能良好。張丹丹［26］和蘇媛媛［14］的試驗研究表明，當排距在4～6倍樁徑時微型抗滑樁組合結構水平承載力最大。

對樁間距的研究雖因試驗或模擬條件的不同稍有差異，但基本認同樁間距為5～6倍樁徑時微型樁抗滑性能較好，GB∕T 38509—2020 建議樁間距不小于5倍樁徑，與前述研究較為相符。

3.5 其他因素

除以上因素外，微型樁的抗彎剛度、施工工藝以及滑體巖土類型等也會影響微型樁的抗滑作用。閆金凱等［33］的試驗顯示，由于不同配筋方式導致抗彎剛度不同，樁周配筋的微型樁在滑面處產生彎剪破壞，而樁心配筋的微型樁在滑面附近發生彎折破壞。滑坡的巖土體類型影響著滑坡的推力分布以及微型樁的受力類型。GB∕T 38509—2020 建議，對硬質巖層滑坡可假定滑坡水平推力均勻分布于各排樁；對軟質巖或風化嚴重的巖層滑坡以及土質滑坡，應考慮作用于各排樁的不均勻性。辛建平等［34］通過數值模擬分析發現不同類型邊坡中微型樁的破壞機制不同，巖土混合邊坡中樁體主要在滑面處和滑面以上分別發生彎剪和彎曲破壞，巖質邊坡中樁體主要發生滑帶處錯動引起的剪切破壞，而土質邊坡中樁體主要發生滑帶兩側的彎曲破壞。施工工藝中注漿的影響也比較大。在高壓注漿作用下，水泥砂漿容易在滑面土層擴散形成水泥土，提高滑面抗剪強度；同時，漿液的填充和擠密作用使巖土體的孔隙減小、密度增大，形成一個擴散復合體，可有效阻止地表水滲入，提高滑坡或邊坡的穩定性［17］。

4 微型樁-連梁組合結構內力計算

針對微型抗滑樁組合結構的內力計算廣泛采用的方法包括平面鋼架計算方法、基于樁土相互作用彈塑性p?y、t?z模型的計算方法以及數值仿真法。

4.1 平面鋼架計算方法

該方法將微型抗滑樁-連梁組合結構簡化為平面鋼架，采用結構力學方法進行求解。馮君等［35］假設樁頂之間為彈性連接，樁與樁周巖土體相互作用采用彈性地基梁K 法或m 法，并且根據巖土體性質假設滑坡推力的分布，通過傳遞系數法計算樁間滑體的剩余下滑力。周德培等［1］假設滑面處為固定端，滑坡推力為均布荷載，地基土的基床系數采用K 法，樁頂軸力根據頂梁的彎矩計算，因此無法分析樁身部分軸力的變化。肖世國等［12］以滑面為界，對上半部分采用側向彈性地基約束的平面鋼架模型，假設巖土推力按三角形分布作用于平面鋼架上，各樁按m 法求解內力；對下部嵌固段根據地層條件采用K 法或m 法計算，通過迭代獲得整體內力計算結果，軸力則通過截面轉角近似計算，與實測對比時發現后緣樁的軸力分布有一定誤差。王金梅等［36］根據微型樁上各部分受力特點的不同，將微型樁分成上部摩擦受拉段、中部滑坡推力作用段和下部錨固段三段進行分析，假設滑坡推力主要作用在滑面上部一定范圍并呈等三角形分布，錨固段受向下的摩擦力作用，水平方向采用橫向受力的彈性地基梁進行分析。該方法的不足是不能考慮微型樁縱橫彎曲作用導致的軸力變化，也沒有擴展至多排樁的情況。此類方法中滑坡推力的大小和分布不能隨著樁和巖土體的變形實時調整，沒有考慮在大變形情況下樁土相互作用的非線性特征，對樁內力的分析沒有考慮樁縱橫彎曲變形的特性，不能真實反映微型樁-連梁組合結構的受力情況。

4.2 基于彈塑性p?y、t?z模型的計算方法

基于彈塑性p?y模型的計算方法能夠較好地計算抗滑樁的橫向變形。其計算原理如圖8（a）所示，將樁土相互作用假設成一系列隨樁身分布的橫向非線性彈簧（即p?y模型），并通過施加土體橫向位移進行計算求解。White等［37］采用LPILE 軟件結合試驗實測p?y模型得到了與試驗吻合較好的計算結果。Lei 等［24］采用雙曲線p?y模型對柔性樁的響應進行了一系列的計算分析。Boeckmann［11］、Sun 等［38］采用p?y法對微型樁的內力進行了計算，但是該方法只能進行單樁計算，沒有擴展至多排樁結構，對于無聯系梁的微型樁計算結果與實測的彎矩分布較為符合，而對于有頂梁的微型樁誤差較大［11］。

采用t?z模型可以對微型樁的軸力分布進行分析，如圖8（b）所示，將縱向樁土相互作用假設成一系列隨樁身分布的縱向非線性彈簧（即t?z模型），彈簧參數根據樁土界面性質確定，通過施加土體縱向位移可求解樁身軸力。Loehr 等［7］采用該方法對傾斜微型樁的軸力進行了較好地預測。但是與p?y模型計算彎矩的效果相比，該方法對軸力的計算效果要差很多，甚至在一些情況下無法獲得正確的軸力方向［11］，主要原因是該方法沒有考慮微型樁縱橫彎曲變形的特性，也沒有合理考慮樁頂約束的影響。

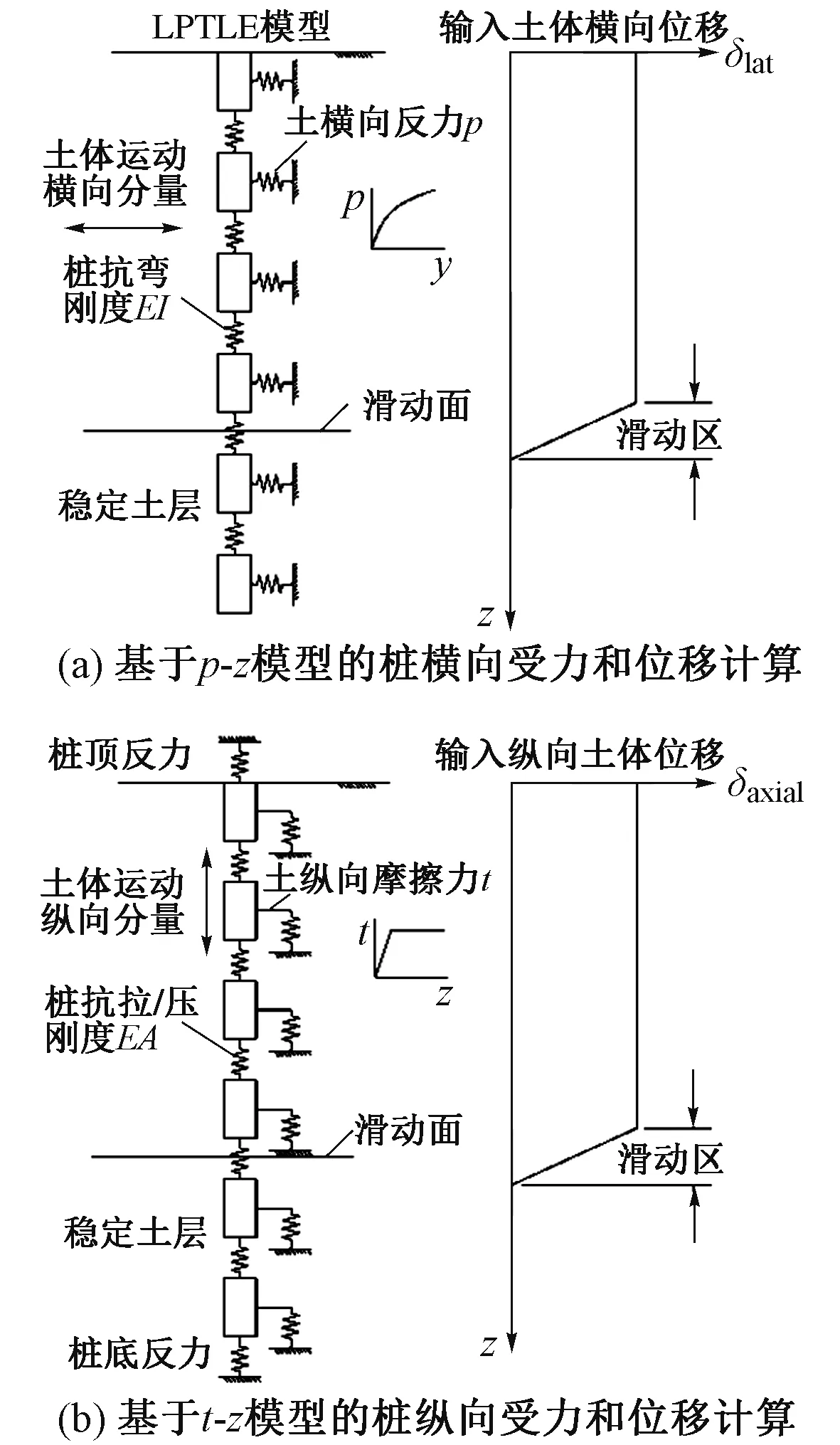
圖8 基于樁土相互作用彈塑性p?y、t?z模型的計算模型

總而言之，該類方法具備較好的可擴展性，能通過技術手段克服前述不足，建立考慮縱橫彎曲變形和連梁作用的基于彈塑性p?y、t?z模型的微型樁組合結構內力計算方法。

4.3 數值仿真法

目前一般采用有限元或有限差分法對微型樁加固邊坡進行數值模擬研究。該方法將樁和土體離散成足夠小的單元體，采用梁單元或彈性實體單元來模擬樁，對巖土單元則采用彈塑性本構模型，滑坡過程采用強度折減法或通過預先設置接觸面單元的形式進行模擬。該方法雖然能較好地還原微型樁加固滑坡的受力過程，但是其精度受諸多因素的影響，如土體的變形和強度參數、本構模型、樁土界面性質等，應通過原位或模型試驗對數值模型進行校核。同時，數值仿真也常作為模型試驗的補充，共同揭示微型樁的加固機理。目前國內外學者雖然通過數值仿真對微型樁的加固機理及影響因素進行了大量研究，但是主要以參數影響規律的定性研究為主，對微型樁樁土相互作用的研究不足，沒有為微型樁-連梁組合結構的內力計算提供樁土相互作用模型。

5 結語

微型抗滑樁-連梁組合結構的研究主要是分析其加固機理及影響因素（樁傾角、樁頂約束、嵌固長度、間距等），并建立合適的內力計算方法進行優化設計。國內外研究人員通過模型和現場試驗以及數值模擬等手段對該結構受力特性進行了大量的研究，提出了平面鋼架計算法以及p?y、t?z模型法等方法。目前的研究表明，微型樁的抗滑承載力由滑面附近樁的剪力及軸力共同提供。由于微型樁縱橫彎曲變形的特性，加上連梁作用帶來的多排樁協調受力的復雜性，目前還不能準確計算微型樁的抗滑承載力，對微型樁臨界嵌固長度的分析還停留在單樁極限分析階段。因此，有必要針對以上問題進行相關的試驗、模擬和理論研究，探尋考慮樁身縱橫彎曲變形的微型抗滑樁-連梁組合結構內力計算方法，對該結構的優化設計提供理論和技術支撐。