基于頂?shù)装鍎偠炔町惖幕炷料淞菏湛s效應(yīng)試驗研究

李珍 周勇軍，2 趙煜，2 衛(wèi)愿康 趙洋

1.長安大學公路學院，西安 710064；2.長安大學公路大型結(jié)構(gòu)安全教育部工程研究中心，西安 710064；3.河南省交通規(guī)劃設(shè)計研究院股份有限公司，鄭州 450052

隨著使用年限的增加，預(yù)應(yīng)力混凝土箱梁出現(xiàn)了不同程度的下?lián)虾烷_裂現(xiàn)象，不僅影響了行車的舒適性，而且降低了結(jié)構(gòu)的耐久性，對橋梁結(jié)構(gòu)的安全運營造成了威脅，后期的維修加固難度風險極大［1］。關(guān)于預(yù)應(yīng)力混凝土箱梁橋的下?lián)虾烷_裂病害，國內(nèi)外專家認為主要有三方面原因：收縮徐變效應(yīng)、鋼筋應(yīng)力松弛、計算方法的差異。其中，收縮徐變的不確定性是導(dǎo)致預(yù)應(yīng)力混凝土箱梁橋長期撓度變形不能準確預(yù)測的主要原因［2］。

關(guān)于混凝土箱梁橋非均勻收縮效應(yīng)，國內(nèi)外學者做了很多研究。文獻［3-8］利用有限元軟件考慮混凝土箱梁不同部位的收縮差異，研究非均勻收縮對混凝土箱梁橋長期下?lián)系挠绊懀l(fā)現(xiàn)考慮非均勻收縮計算的跨中撓度比不考慮時大，計算模型較好地模擬了實際箱梁橋收縮特性。文獻［9］進行了工字型構(gòu)件的非均勻試驗，并基于濕度場理論考慮箱梁橋的非均勻收縮效應(yīng)，發(fā)現(xiàn)箱梁截面非均勻收縮會產(chǎn)生撓曲變形。而文獻［10-11］的研究結(jié)果卻表明混凝土箱梁橋各部位收縮差異對主梁下?lián)蠋淼挠绊戄^小。由此可見，對非均勻收縮引起的混凝土箱梁橋長期撓曲變形問題還沒有統(tǒng)一的結(jié)論，并且缺乏箱梁收縮試驗驗證。

本文通過不同頂?shù)装鍎偠认碌幕炷料淞菏湛s效應(yīng)試驗，基于濕度場理論，采用有限元軟件對節(jié)段箱梁收縮效應(yīng)進行模擬，研究構(gòu)件的收縮曲率變化規(guī)律并與試驗結(jié)果對比分析，研究成果可為混凝土箱梁橋長期撓曲變形提供參考。

1 試驗概況

1.1 試驗構(gòu)件的設(shè)計與制作

試驗只考慮頂?shù)装鍎偠龋ê穸龋┎町悓ο淞菏湛s效應(yīng)的影響。對于實際工程中的大跨度混凝土箱梁，一般頂板厚度為250 mm 左右，底板厚度為200～1 000 mm，頂?shù)装搴穸缺仍?∶1～1∶4。因此，本文選擇頂?shù)装搴穸缺葹?∶1、1∶2、1∶3的三組節(jié)段箱梁構(gòu)件進行試驗，頂?shù)装鍎偠缺确謩e為1∶0.6、1∶4.8、1∶16.2，試驗組編號分別為BS?60、BS?120、BS?180，每組三個構(gòu)件，見圖1。三組構(gòu)件頂板、腹板尺寸厚度均為60 mm，底板厚度分別為60、120、180 mm。節(jié)段箱梁構(gòu)件均豎直放置，自重作用引起試驗構(gòu)件的徐變變形很小，可忽略不計。

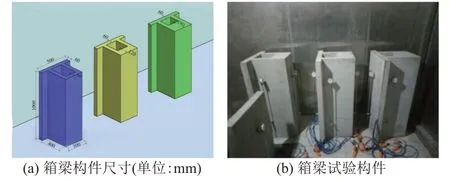
圖1 試驗構(gòu)件

1.2 混凝土材料及配合比設(shè)計

混凝土設(shè)計強度等級為C50，配合比見表1。混凝土節(jié)段箱梁澆筑成型后，設(shè)置環(huán)境實驗室內(nèi)為標準養(yǎng)護條件［（溫度為（20 ± 2）℃、相對濕度為95%以上］，養(yǎng)護3 d 后，安裝并調(diào)試測試裝置，將環(huán)境條件設(shè)置為測試條件［溫度為（20±2）℃、相對濕度為（60±5）%］開始進行收縮測試，此后控制測試環(huán)境為恒溫恒濕。

表1 混凝土配合比

1.3 試驗測試

測試箱梁各部分的應(yīng)變，并實時監(jiān)測溫度、濕度。混凝土內(nèi)部采用內(nèi)部預(yù)埋振弦式應(yīng)變計和外部大標距引伸計（千分表）進行應(yīng)變測量。測點布置見圖2。

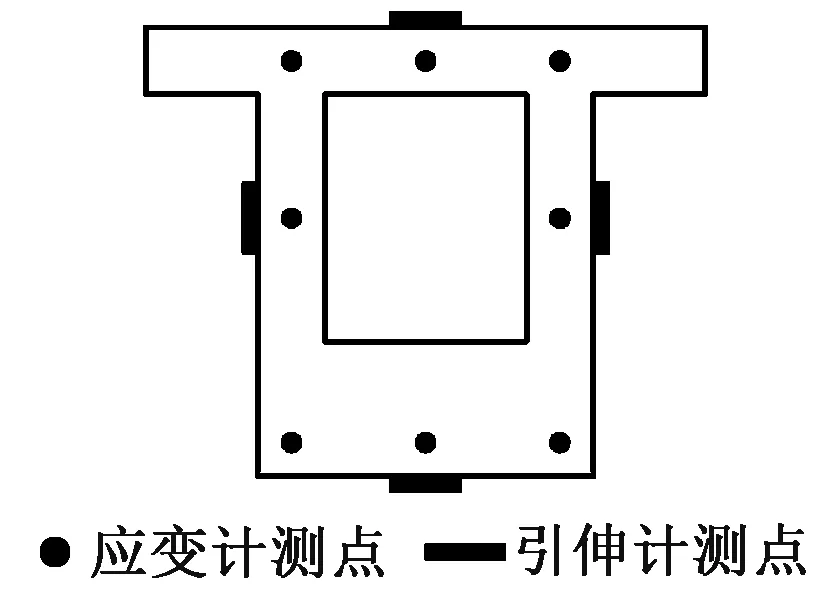
圖2 箱梁測點布置

2 試驗結(jié)果與分析

混凝土箱梁頂?shù)装宓氖湛s應(yīng)變?nèi)?個內(nèi)部預(yù)埋振弦式應(yīng)變計測得的平均值。左右腹板收縮應(yīng)變?nèi)∠鄳?yīng)板件中部的1 個內(nèi)部預(yù)埋振弦式應(yīng)變計測試值，同時用外部的引伸計對內(nèi)部振弦式傳感器讀數(shù)進行校準。試驗結(jié)果取一組3個構(gòu)件的算術(shù)平均數(shù)作為該混凝土在各齡期時的收縮應(yīng)變。由于混凝土構(gòu)件、振弦式應(yīng)變計鋼弦和大標距引伸計的線膨脹系數(shù)不同，在試驗過程中，若環(huán)境溫度前后兩次存在差值，兩者產(chǎn)生的熱脹冷縮變形會有所差異。因此，在實際測量值中包含了由于溫度變化造成的應(yīng)變差，須對其進行溫度修正。節(jié)段箱梁構(gòu)件共監(jiān)測了90 d。

2.1 箱梁構(gòu)件收縮試驗結(jié)果

箱梁構(gòu)件實測收縮應(yīng)變發(fā)展曲線見圖3。可知：①BS?60 組箱梁各部位收縮規(guī)律基本一致，各齡期收縮應(yīng)變差較小，表明頂?shù)装逶谑湛s歷程中近似呈均勻收縮；箱梁各部位前期收縮發(fā)展速度快，后期收縮速度減緩，最終趨于平穩(wěn)狀態(tài)。②BS?120 組箱梁頂板和底板收縮規(guī)律存在差異，頂板在各齡期的收縮應(yīng)變均比底板大，頂?shù)装宄史蔷鶆蚴湛s。在收縮發(fā)展前期，頂?shù)装宓氖湛s應(yīng)變差隨著齡期增大而增大，在齡期達到30 d 左右時收縮應(yīng)變差達到極值，后期收縮應(yīng)變差減小，這表明頂板早期收縮發(fā)展迅速而后期減緩，底板則因厚度大，前期收縮發(fā)展緩慢，后期仍有發(fā)展趨勢。③BS?180 組箱梁頂板與底板的收縮應(yīng)變差比BS?120 組更大，箱梁頂?shù)装宓姆蔷鶆蚴湛s更加明顯。與BS?120組不同的是，箱梁頂?shù)装迨湛s應(yīng)變差達到極值的齡期不同，因為BS?180 組底板更厚，底板收縮發(fā)展相對緩慢，所以達到收縮應(yīng)變差極值的時間有所推遲，齡期50 d左右時到達最大。

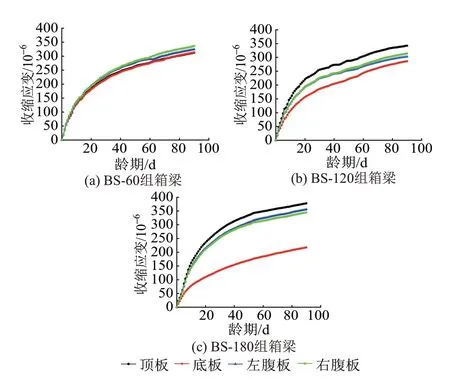
圖3 箱梁構(gòu)件實測收縮應(yīng)變發(fā)展曲線

2.2 箱梁構(gòu)件收縮曲率

不同頂?shù)装鍎偠缺葘?jié)段箱梁曲率的影響不同，節(jié)段箱梁的頂?shù)装迨湛s應(yīng)變差表明了箱梁構(gòu)件在試驗期間不僅發(fā)生軸向縮短，還發(fā)生了彎曲變形，這種彎曲變形的程度可用曲率表示。在平截面假定的情況下，曲率κ只和頂?shù)装宓膽?yīng)變差有關(guān)，其計算式為

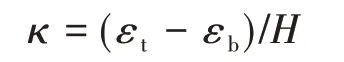
式中：εt、εb分別為頂板、底板的收縮應(yīng)變；H為箱梁截面高度。

箱梁構(gòu)件收縮曲率曲線見圖4。可知：①頂?shù)装鍎偠缺葘?jié)段箱梁收縮產(chǎn)生的曲率有較大影響。當頂?shù)装鍎偠炔町惒淮髸r，箱梁收縮基本上不產(chǎn)生額外的曲率；當頂?shù)装鍎偠炔町愝^大時，收縮差異會導(dǎo)致曲率變化較大。箱梁收縮前期曲率增長較快，隨著齡期的發(fā)展，增長速率減緩，達到曲率峰值點后開始減小，但是減小速率較慢。②箱梁曲率達到峰值點的時刻與頂?shù)装鍎偠认嚓P(guān)，頂?shù)装鍎偠炔町愒酱螅酵磉_到峰值點，BS?120 組箱梁構(gòu)件在30 d 齡期達到峰值，BS?180 組則在53 d 到達峰值。③曲率峰值隨頂?shù)装鍎偠炔町惖脑龃蠖龃螅珺S?180 組的曲率峰值是BS?120組的2倍以上。

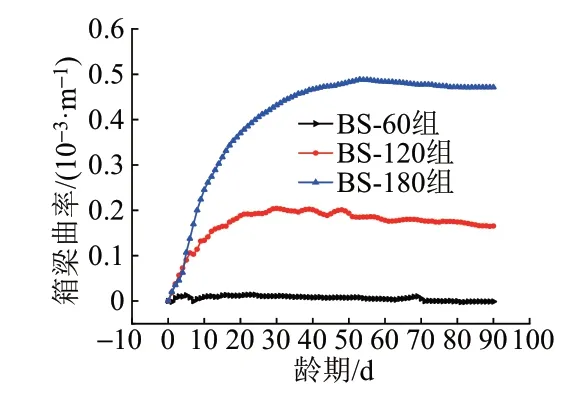
圖4 箱梁構(gòu)件收縮曲率曲線

2.3 典型收縮預(yù)測模型計算值與實測值對比分析

計算箱梁收縮通用的理論方法是將箱梁全截面的理論厚度作為計算基礎(chǔ)。該理論模型采用JTG 3362—2018《公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計規(guī)范》［12］中的模型。

為了驗證箱梁各部位收縮的差異性，將頂?shù)装鍖崪y應(yīng)變和全截面理論應(yīng)變進行對比，見圖5。可知，按照規(guī)范全截面理論計算的頂?shù)装迨湛s值與實測值差距較大，說明與實際情況不相符，且頂板理論計算值與實測值的相對誤差普遍比底板大，最高可達50%以上。

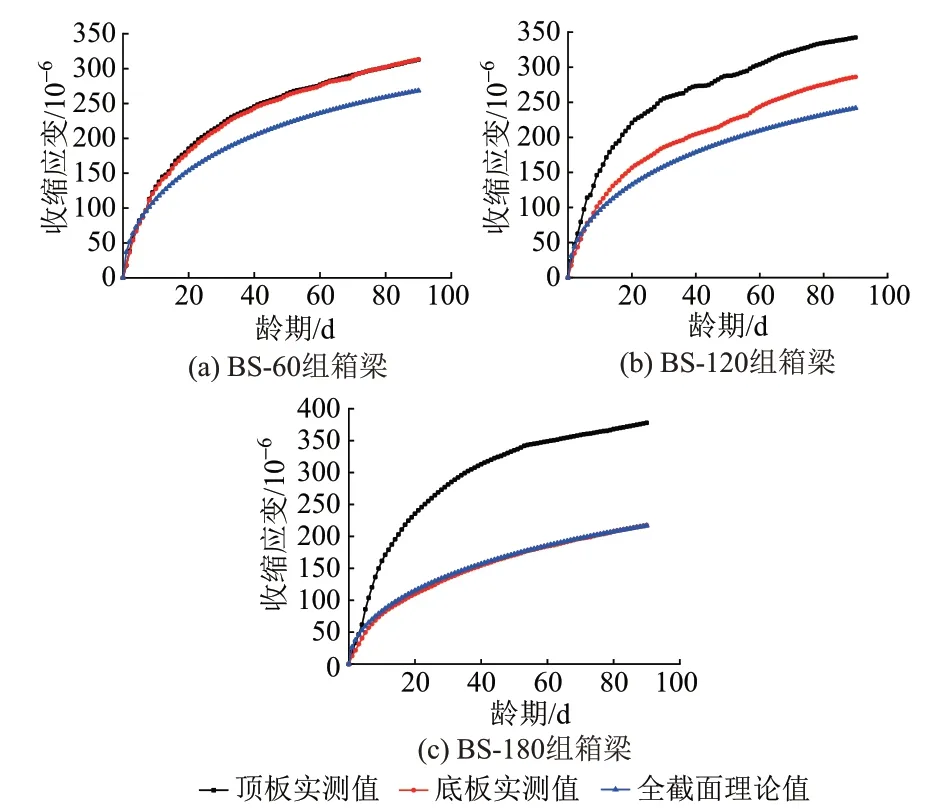
圖5 各組箱梁收縮實測值與模型理論計算值對比

3 節(jié)段箱梁在濕度場下的收縮效應(yīng)分析

混凝土在干燥、硬化過程中，結(jié)構(gòu)內(nèi)部和外界環(huán)境在濕度梯度下不斷地發(fā)生水分轉(zhuǎn)移，直到內(nèi)外濕度達到平衡。混凝土內(nèi)部濕度變化引起了體積變化，導(dǎo)致結(jié)構(gòu)產(chǎn)生非均勻收縮變形。這一過程中內(nèi)部水分擴散服從Fick定律［13-15］，因此，可通過濕度場理論對混凝土構(gòu)件的收縮過程進行計算分析，研究混凝土內(nèi)部濕度擴散過程和混凝土箱梁結(jié)構(gòu)的非均勻收縮規(guī)律。

3.1 混凝土濕度場模擬

混凝土的濕度場可以用溫度場替代求解，但前提是把兩個場的各物理量對應(yīng)起來。通過對比發(fā)現(xiàn)，相對濕度對應(yīng)于溫度，濕度擴散系數(shù)可用導(dǎo)溫系數(shù)替代，表面因子可用熱交換系數(shù)替代，收縮系數(shù)可用熱膨脹系數(shù)替代［16］。本文通過ABAQUS 有限元軟件進行混凝土濕度場下收縮效應(yīng)的求解與分析。

3.2 計算參數(shù)的選擇及基本假定

混凝土濕度場的主要計算參數(shù)如濕度擴散系數(shù)、表面因子和收縮系數(shù)，與試驗材料和環(huán)境因素有關(guān)，很難確定其精確數(shù)值。因此，如要對混凝土濕度場下的收縮效應(yīng)進行精確模擬，必須選擇合適的計算參數(shù)，因此作如下假定與參數(shù)取值說明：

1）試驗采用的材料是水膠比較大的普通混凝土，因此只考慮由于水分散發(fā)引起的干燥收縮，不考慮其他類型的收縮；試驗的環(huán)境溫度為標準試驗溫度，且試件較小、水化熱少，忽略溫度對濕度場的影響。

2）濕度擴散系數(shù)D（H）取常數(shù)，收縮應(yīng)變與濕度之間的關(guān)系采用線性模型。

3）表面因子f和收縮系數(shù)ksh根據(jù)試驗結(jié)果進行反演分析獲得。

4）收縮應(yīng)變主要由濕度變化和收縮系數(shù)確定，與彈性模量相關(guān)性不強，所以假定混凝土收縮過程中彈性模量為定值。

國內(nèi)外有關(guān)研究表明，濕度擴散系數(shù)D(H)、表面因子f和收縮系數(shù)ksh在試驗條件下無法確定時，其數(shù)值 參 考 范 圍［16］為：12 ≤D(H)≤360，0.05 ≤f≤80，0.5× 10-3≤ksh≤3× 10-3。

在給定參數(shù)范圍內(nèi)根據(jù)試驗數(shù)據(jù)進行濕度場的計算參數(shù)反演，得到能準確模擬試驗過程的計算參數(shù)，其中濕度擴散系數(shù)因缺乏試驗數(shù)據(jù)，可取中位數(shù)。參數(shù)試算流程見圖6。

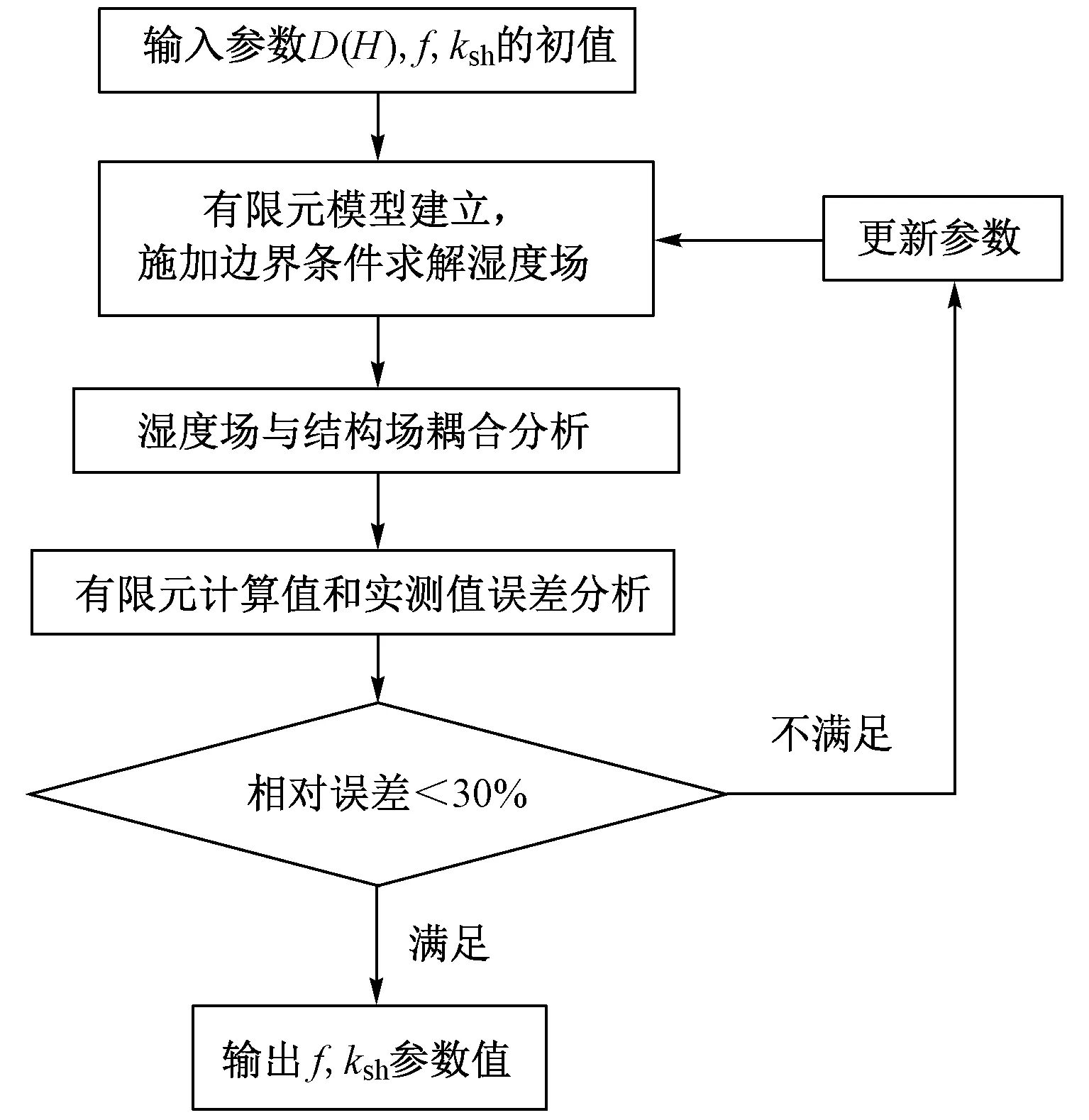
圖6 參數(shù)試算流程

具體步驟為：將混凝土材料屬性中的密度和比熱容都設(shè)為1，將濕度場和溫度場對應(yīng)起來，假定f、ksh參數(shù)值進行濕度場的求解。利用熱-位移耦合關(guān)系計算收縮效應(yīng)，將有限元計算值與實測值進行對比，使兩者接近。建立兩個分析步模擬試驗過程的環(huán)境情況，分別為構(gòu)件養(yǎng)護階段和測試階段。經(jīng)計算分析選取后，節(jié)段箱梁濕度場的計算參數(shù)見表2。

表2 混凝土濕度場計算參數(shù)

將箱梁頂?shù)装鍖崪y收縮應(yīng)變曲線與有限元計算收縮應(yīng)變曲線進行對比，見圖7。可知，在有限元計算結(jié)果中，BS?60 組箱梁頂?shù)装迨湛s發(fā)展趨勢基本一致，BS?120組箱梁、BS?180組箱梁的頂板和底板收縮規(guī)律不同，頂板的收縮應(yīng)變比底板大，頂板的收縮速率逐漸減小，而底板基本上成線性發(fā)展，這與實測值基本一致。誤差在13%~30%。

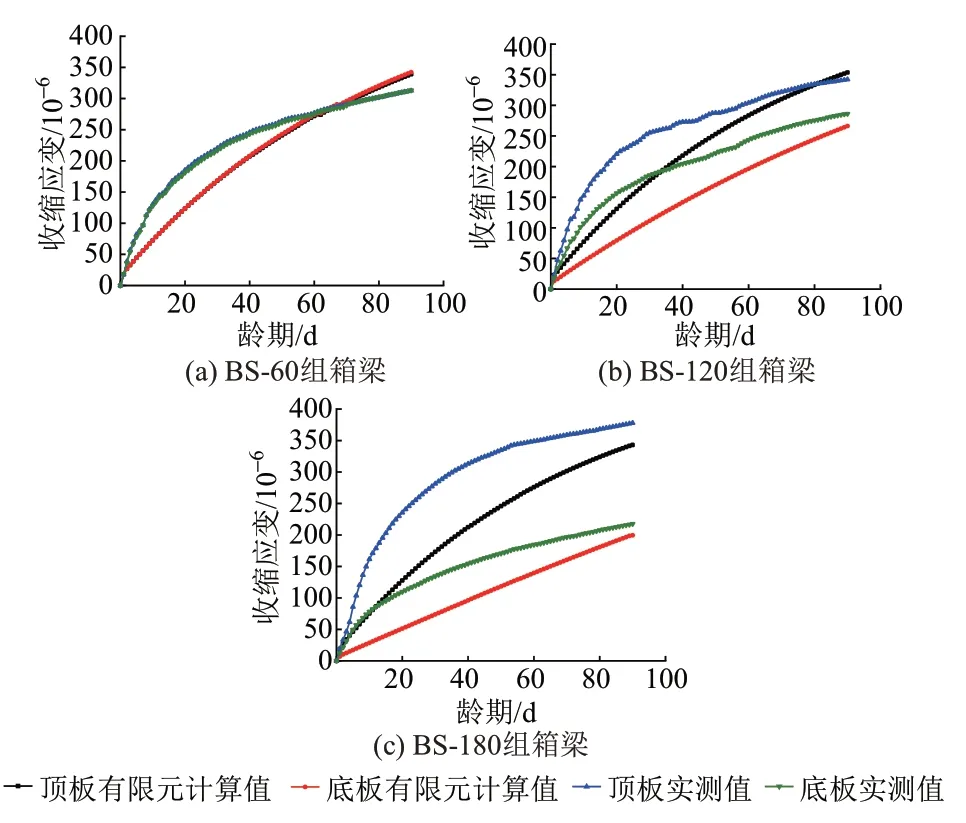
圖7 箱梁頂?shù)装迨湛s應(yīng)變有限元計算值和實測值對比

3.3 濕度場模擬結(jié)果

三組箱梁在第90 天的濕度分布云圖見圖8。可知：混凝土的濕度擴散速度隨深度的增加而減小，由于表面直接與空氣接觸，所以濕度散失較快，內(nèi)部濕度到達表面的路徑較長，因此濕度變化較緩慢；隨著頂?shù)装鍎偠炔町惖脑龃螅淞航孛娴臐穸忍荻仍龃蟆?/p>

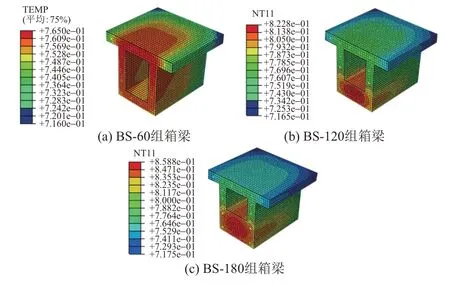
圖8 箱梁構(gòu)件90 d濕度分布云圖

箱梁曲率有限元計算值與實測值對比見圖9。可知，二者變化規(guī)律基本一致，且誤差在一定范圍之內(nèi)，表明采用濕度場模擬節(jié)段箱梁的收縮曲率具有可行性；箱梁曲率有限元計算值與實測值的差異主要體現(xiàn)在峰值曲率以及峰值出現(xiàn)時間。對于數(shù)值上的差異，主要是由于各組箱梁之間材料的不均勻、試驗過程中周圍環(huán)境的變化導(dǎo)致的。對于峰值出現(xiàn)時間，這是由于試驗過程中打開了循環(huán)風機，風速加速了箱梁的收縮。

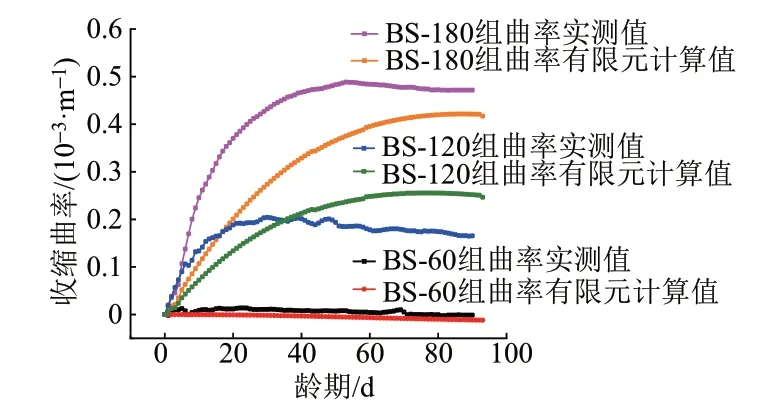
圖9 箱梁曲率有限元計算值與實測值對比

4 結(jié)論

1）節(jié)段箱梁的頂?shù)装鍎偠炔煌瑫r，其產(chǎn)生的收縮規(guī)律不同。當頂板和底板的剛度差異較小時，箱梁的各部位收縮基本同步發(fā)展，只產(chǎn)生軸向變形，不產(chǎn)生額外的曲率。

2）當頂板和底板的剛度差異較大時，各部位產(chǎn)生收縮應(yīng)變差，從而導(dǎo)致節(jié)段箱梁產(chǎn)生收縮曲率。曲率呈先增大后減小的變化趨勢，收縮曲率達到峰值的時間不一致，頂?shù)装鍎偠炔町愒酱螅溥_到峰值的時間越晚，但其相應(yīng)的曲率極值越大。

3）按照全截面計算箱梁收縮值與頂?shù)装宓膶嶋H收縮值差距較大。

4）濕度梯度是箱梁截面產(chǎn)生收縮差異的直接原因。采用濕度場模擬所得箱梁收縮曲率與實測值基本一致，且誤差在一定范圍之內(nèi)，該方法具有可行性。