基于隨機森林算法的在線軌道平面線形判別方法

秦哲 杜馨瑜 李穎 王昊

1.中國鐵道科學研究院研究生部，北京 100081；2.中國鐵道科學研究院集團有限公司基礎設施檢測研究所，北京 100081

鐵路軌道的平面線形一般分為直線、緩和曲線、圓曲線三種。在列車動力作用下，曲線軌道的變形不斷累積，容易出現方向錯亂。為確保行車安全平穩，須定期檢查曲線方向，必要時進行曲線整正，使其恢復到原設計位置。軌道平面曲線的穩定性、平順度和正確的幾何形位直接影響到列車的運行速度和運行安全［1-2］。

現有軌道平面線形判別參數可以識別出半徑在150~8 000 m的曲線，但對于半徑8 000 m以上的曲線須要更換軌道平面線形判別參數［3］。余寧等［4］提出的基于卷積神經網絡的鐵路曲線特征點檢測算法可以進行離線軌道平面線形判別，但無法嵌入到目前實際使用的實時軌道幾何參數檢測系統GJ?6中，不具備現場檢測實用性。

本文利用軌道平面線形判別參數與曲線半徑之間的關系，針對性地設計多維特征，并設計在線隨機森林分類算法嵌入到軌道幾何參數實時檢測系統GJ?6 中，以實現自動切換軌道平面線形判別參數，提高軌道平面線形判別的準確率。

1 軌道平面線形判別方法

1.1 檢測系統工作原理

最新研制的數字式軌道檢測系統將多個分立式的慣性傳感器集成為整體組件，安裝于檢測梁上，如圖1 所示。該系統結構簡單，全部采用數字信號進行傳輸，有效避免了模擬信號在較長傳輸路徑上的電磁干擾，且信號的分辨率顯著提高，同時檢測精度有所提升［5-6］。

圖1 數字式軌道檢測系統檢測梁及懸掛裝置

用于軌道平面線形判別的輸入參數為曲率和曲率變化率。數字式軌道檢測系統搖頭陀螺位于檢測梁中心，其輸出信號經過抗混疊濾波器后進行0.25 m間隔的空間采樣，再經過數字補償濾波器消除速度對信號的影響，最后計算得到曲率和曲率變化率，計算公式為

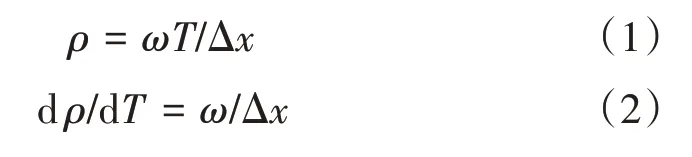
式中：ρ為曲率；dρ為曲率變化率；ω為搖頭角速率；T為采樣時間間隔；Δx為采樣空間間隔。

1.2 軌道平面線形判別

數字式軌道檢測系統的軌道平面線形判別方法和關鍵參數與文獻［3］基本一致，其中關鍵參數為曲率變化跟蹤量調整值、曲率變化跟蹤量閾值、范圍外曲率變化率閾值、范圍內曲率變化率閾值。為判別半徑R＞8 000 m 的軌道平面曲線，須手動切換上述關鍵參數。為了提高軌道平面曲線判別的準確性與簡易性，本文提出使用隨機森林算法根據平面曲線半徑分類結果對關鍵參數進行實時切換的方法。

2 隨機森林算法的引入

隨機森林算法是以決策樹為基學習器的集成監督學習算法，其具有一定的抗噪聲能力，可以處理非線性數據和高維數據，對數據集的適應能力強，訓練速度快，實現簡單，精度高［7-8］。基于該算法的曲線半徑判別主要包含三個步驟：數據預處理、特征提取、模型訓練和測試。

2.1 數據預處理

根據設備臺賬和軌道幾何檢測數據匹配曲線的起點和終點里程，生成曲線半徑識別標準數據庫，流程如圖2所示。

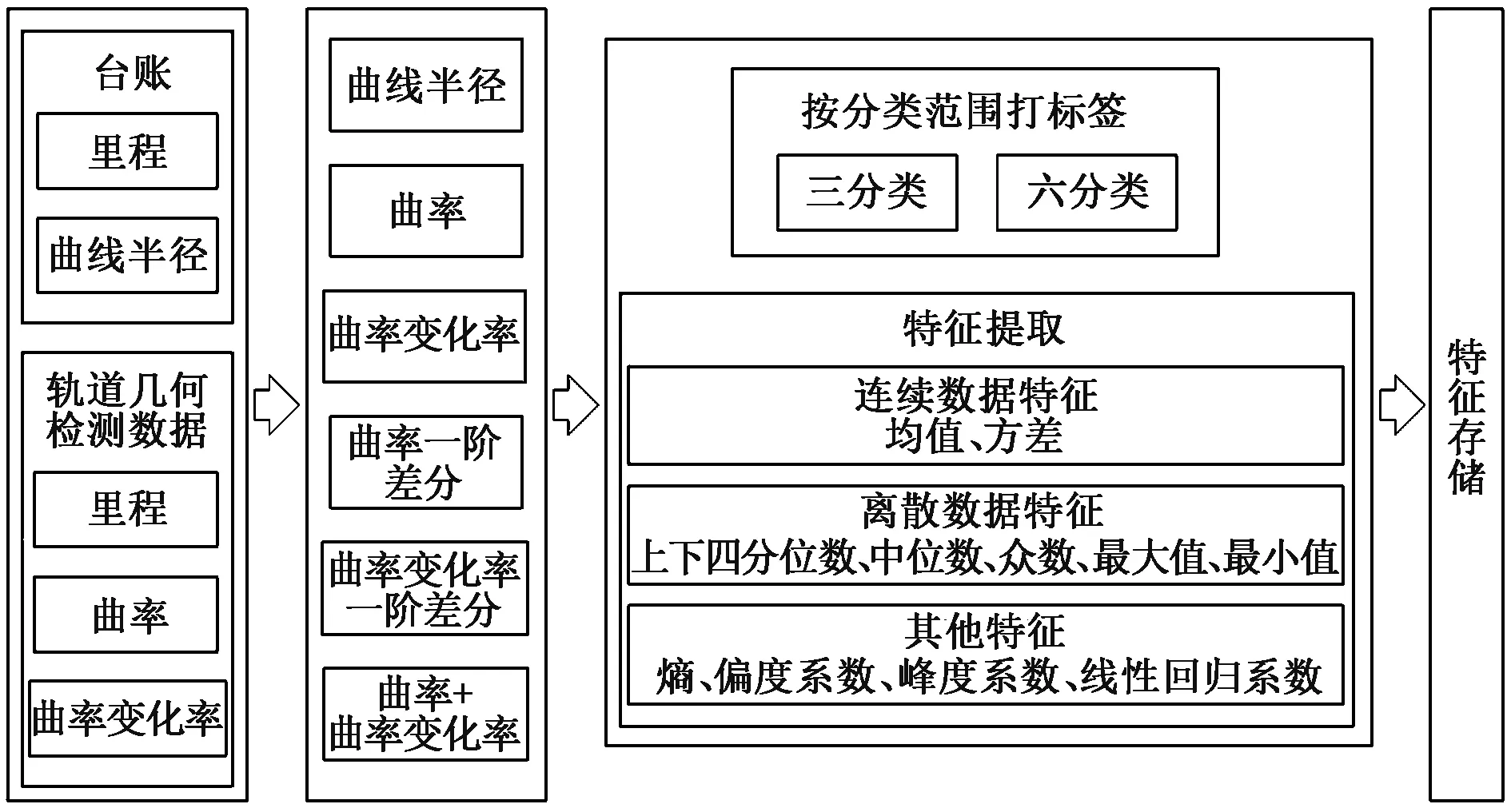
圖2 生成曲線半徑識別標準數據庫流程

2.2 特征提取

按150個采樣點的長度對每條曲線的檢測數據進行分段，對分段后的數據進行特征提取。在不同的曲線半徑下，現有平面曲線分段數據（曲率A1和曲率變化率A2）的特征包括：①典型連續數據特征Ac——均值、方差；②典型離散數據特征Ad——上四分位數、下四分位數、中位數、眾數、最大值、最小值；③其他特征Ao——熵、偏度系數、峰度系數、線性回歸系數。由于這些特征都有顯著的差別，故一列特征有12 個特征值，可表示為Ai=[AcAdAo]T。根據經驗，設計并引入曲率一階差分A3、曲率變化率一階差分A4、曲率+曲率變化率A5三列特征，共計五列特征60 個特征值，可表示為A=[A1A2A3A4A5]。

按分段數據所屬半徑類別對其進行標注，從0 開始，依次遞增。三類平面曲線（R≤3 000、3 000 ＜R≤8 000、R＞8 000）的類別標簽分別是0、1、2；六類平面曲線（R≤1 000、1 000 ＜R≤3 000、3 000 ＜R≤5 000、5 000 ＜R≤8 000、8 000 ＜R≤15 000、R＞15 000）的標簽分別是0、1、2、3、4、5。

2.3 模型訓練和測試

對數據特征進行隨機劃分，70%做模型訓練，剩余30%做測試。模型訓練和參數尋優實現過程如下。

1）從原始訓練集中使用自助法（Bootstrapping）有放回地隨機取出m個樣本［9］，共進行Ntree次采樣，生成Ntree個訓練集，對應隨機森林中Ntree顆決策樹；

2）對Ntree個訓練集分別訓練決策樹模型；

3）對于單顆決策樹，假設訓練樣本特征的個數為n，那么每次分裂時根據信息增益、信息增益比或Gini指數［10］選擇最好的特征進行分裂；

4）對于每棵樹都要依次分裂下去，直到該節點的所有訓練樣本都屬于某一類；

5）將生成的多顆決策樹組成隨機森林。

最終隨機森林的分類實際上是多棵樹分類器投票決定的分類結果。隨機森林構建過程中須設置幾個關鍵參數，主要包括決策樹個數、最大樹深度、葉節點最少樣本數、分裂時最大特征數等。這些參數的選取對進一步提升分類性能具有重要作用，選取順序如下。

1）調整既不會增加模型復雜度又對模型影響最大的參數Ntree，通過學習曲線尋找最佳參數；

2）調整最大樹深度，通過網格搜索或學習曲線判斷；

3）依次對其他參數進行尋優。

為增加模型的魯棒性（robustness），設計并實現了增量訓練［11］。基于某個訓練好的模型，讓模型在原有結構不變的基礎上新增對新軌道數據的特征表達。增量訓練過程的實施步驟如下。

1）選擇一個基于不同軌道數據訓練好的模型；

2）對新增軌道數據進行分段和特征提取；

3）把新增軌道的特征作為訓練集，在已有模型的結構上進行再訓練，讓模型添加對新增數據的表達；

4）保存增量訓練后的模型。

3 應用測試

3.1 離線測試

用離線測試來驗證模型分類的準確率。基于同一線路數據的內部測試結果見表1。其中，Z160、K120、G250、K160、G200 分別代表所選取的160 km∕h鐵路干線、120 km∕h 鐵路線路、250 km∕h 客運專線、160 km∕h 客運專線、某200 km∕h 客運專線；準確率是200 次隨機測試的平均值。由于K120 在三分類中都屬于第一類，故不做三分類測試。

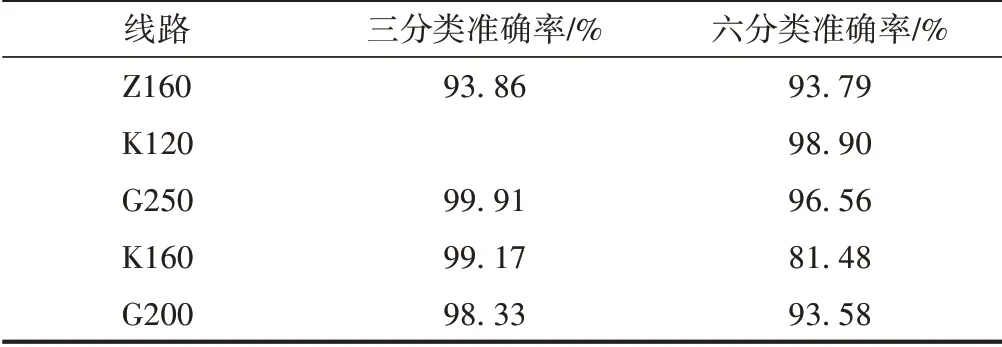
表1 同一線路數據內部測試結果

融合不同線路進行增量訓練測試，內部測試結果見表2。其中準確率是200 次隨機測試的平均值。可以看出，三分類的準確率較高，均大于90%。

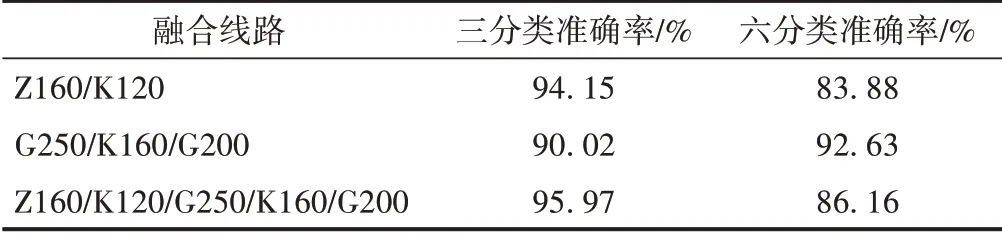
表2 多線路數據融合內部測試結果

3.2 在線測試

由于離線測試結果顯示三分類的準確率較高，將訓練好的三分類模型嵌入到軌道檢測系統軌道幾何參數實時處理軟件中，使系統在運行過程中每150 個采樣點輸出一次曲線半徑分類結果，并根據分類結果自動改變軌道平面線形判別關鍵參數。每個分類結果對應的關鍵參數見表3。

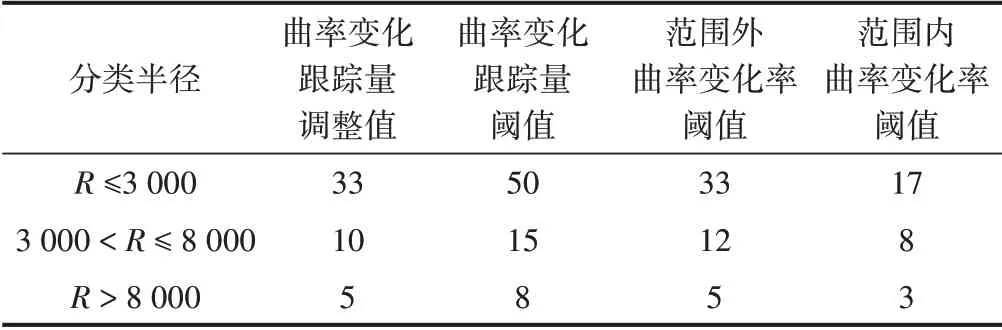
表3 分類結果對應的關鍵參數

選取某200 km∕h 客運專線K8—K80 區段的檢測數據，利用基于隨機森林算法的軌道平面線形判別方法在GJ?6 型軌道幾何參數實時檢測處理軟件中進行測試，并與按照現有軌道平面線形判別方法得出的檢測結果進行對比，結果見圖3。可以看出：根據設備臺賬數據，該區段線路中軌道平面曲線半徑在1 200 ~12 000 m，共12 條；現有軌道平面線形判別方法僅能識別5條曲線，難以判別出R＞6 000 m的曲線；基于隨機森林算法的軌道平面線形判別方法能夠判別出全部12條曲線。

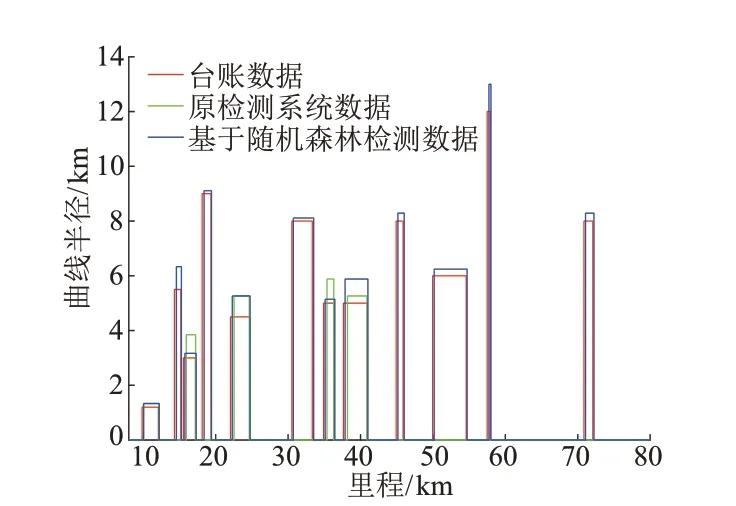
圖3 基于隨機森林算法的在線軌道平面曲線判別結果

4 結語

本文提出了基于隨機森林算法的在線軌道平面線形判別方法，其在方法上的創新主要體現在設計并提取針對性的特征，離線識別準確率提升至90%以上；在應用上的創新主要體現在該算法可以嵌入目前的實時軌檢系統GJ?6中，實現了軌道平面線形判別關鍵參數的自動切換，能夠判別出所有曲線。在測試過程中發現原算法與新算法都存在軌道平面曲線半徑大小計算不準確的問題，下一步應結合軌道檢測系統超限判斷算法進行深入研究。