SOLO分類理論在高中物理復習中的應用①
——以“圓周運動”為例

李國榕 唐 政 張念依 鄧楚楚 林 琪 葉晴瑩

(1.福建師范大學物理與能源學院,福建 福州 350117;2.福建省福州市金山中學,福建 福州 350008)

無論對于哪一學科而言,復習課都是教學的重要組成部分,運用科學有效的教學方法,能更好地培養學生的核心素養、提高學習效率。在同一個班級中,出現學生學習水平不平衡是正常現象,教師在復習課時可以根據學生的不同學習水平采取不同的教學方法,提高學生的復習效率,但如何將學生的水平進行劃分又是教師在教學過程中要面對的難題。

中學物理教育應注重對學生科學思維能力的培養,針對不同學習水平的學生采用合適的教學方法是提高學生學習能力的關鍵。將SOLO分類理論運用于復習課的教學中,有助于教師分析學生學習水平層次,建立最近發展區,提高學生的學習能力。

1 SOLO分類理論簡介

SOLO(Structure of the Observed Learning Outcome)分類理論由澳大利亞心理學家比格斯(J.B.Biggs)率先提出，可譯為“可觀察的學習結果的結構”，他將學生的學習結果由低到高分為五個層次水平。

(1)前結構水平:面對問題時學生無法理解、解釋或者答非所問。

(2)單點結構水平:學生能從問題中找到一個解題條件,直接從該單一條件得出答案。

(3)多點結構水平:學生能夠找到多個解題條件,聯想到相關的知識,但不能將這些知識進行有機整合。

(4)關聯結構水平:學生能夠從多個角度對問題進行分析,能將各種有效信息結合起來思考,解決較為復雜的問題。

(5)拓展抽象水平:學生能夠將接觸過的問題遷移到新的情景中,并且能夠得到具有開放性的結論,概括出更抽象的本質屬性,使問題本身的意義得到拓展。

這五個水平層次體現了學生對事物的理解階段:我不理解它——我知道了一個方面——我知道了大多數——我知道它們是怎么結合到一起的——我明白這個可以在多種情況下運用。

2 SOLO分類理論在“圓周運動”復習課中的應用

SOLO分類理論將學習者的學習水平劃分成為層級結構,意味著學習者的學習水平是由低級向高級、形象到抽象逐步發展的。教師可依據學生的學習表現判斷學生處在哪個層次水平,從而設計物理教學,本文以魯科版必修二第四章“圓周運動”的復習課為例。

2.1 前結構水平

在學習完“圓周運動”后,教師要想了解學生的學習水平，可以先通過基礎知識開始,向學生提問:什么是勻速圓周運動?若有學生連這個問題都回答不出來,或者回答根本就與勻速圓周運動無關，教師可判斷該學生處于前結構水平。

教師可以從基本概念入手,幫助學生建立基本的知識體系。首先可以列舉一些生活中圓周運動的實例:摩天輪、過山車、月球繞地球運轉等,再引出勻速圓周運動的定義:在任意相等時間內通過的弧長都相等的圓周運動叫做勻速圓周運動。通過實例與圖像相結合,讓學生逐漸建立起圓周運動的基本概念,順利將學生推向更高的學習水平。

2.2 單點結構水平

處在單點結構水平的學生,在物理學習上主要表現為：能用一個相關知識點解釋物理現象,對現象進行簡單分析,但分析過程會出現前后矛盾。例如對于勻速圓周運動,有些學生則會抓住“勻速”二字,從而認為勻速圓周運動是勻速運動,表明學生處在單點結構水平，這一類型的學生思維單一,不會從多角度思考問題。

對于這種學習水平的學生,在教學中可以適當地對學生進行引導，可提示學生:速度是矢量,既有大小又有方向,“勻速運動”是指速度大小和方向都不變的運動,而勻速圓周運動是曲線運動,速度大小不變,但速度方向不斷改變,所以勻速圓周運動的速度是變化的。

2.3 多點結構水平

學生對待物理問題能從多個角度出發,提取相應的物理量,但不能將這些物理量整合起來解決問題，下面以一道例題為例予以說明。

例1:如圖1所示,光滑圓軌道半徑為R,軌道AB光滑,軌道BC水平長度為s，動摩擦因數為μ,為使小球能夠通過圓軌道的最高點D,小球從AB上下滑的高度至少為多少？

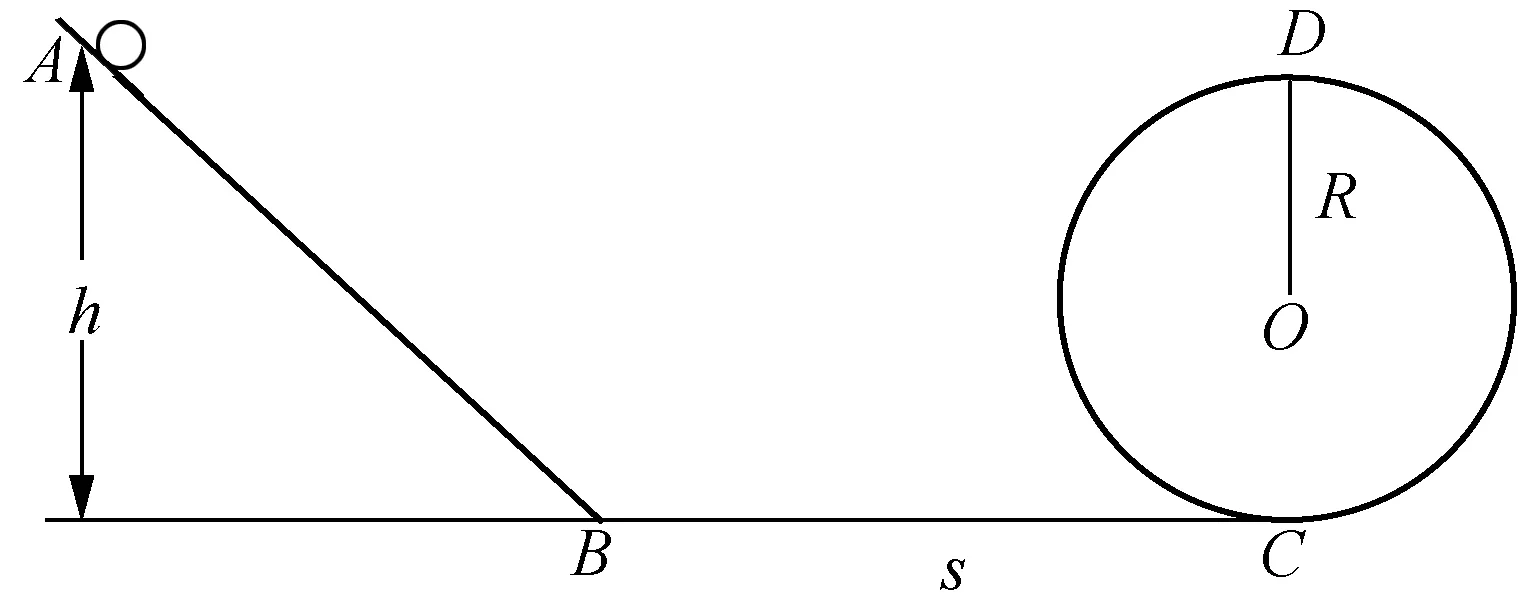
圖1

對于這類臨界問題，學生能解決以下幾個問題：(1)在AB段只有重力做功,在BC段摩擦力做負功;(2)能正確分析小球在圓周的最低點、最高點的受力情況;(3)能夠用語言或者公式描述動能定理。但僅僅是簡單羅列,不能將它們結合起來解決問題。

處于多點結構水平的學生能提取的知識較為零散,教師要著力于幫助學生進行知識的遷移,建立知識之間的聯系,讓學生的知識形成網絡、融會貫通。

2.4 關聯結構水平

處于該水平的學生在物理學習上主要表現為：能從物理問題中提取全部或大部分有效信息,有條理、嚴密地解決問題。當處于此層次水平的學生遇到上述例題時,能夠給出小球恰好能夠通過最高點時的速度大小,判斷出小球從軌道由靜止下滑到圓的最高點的過程中各力做功的情況,會應用動能定理解決問題。

教師不僅要求這類學生會做題,還應要求學生建立物理模型,以提高學生的思維水平。對于上述圓周運動臨界問題,當小球通過最高點時,會出現以下兩種臨界狀態:

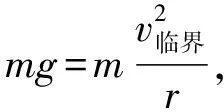
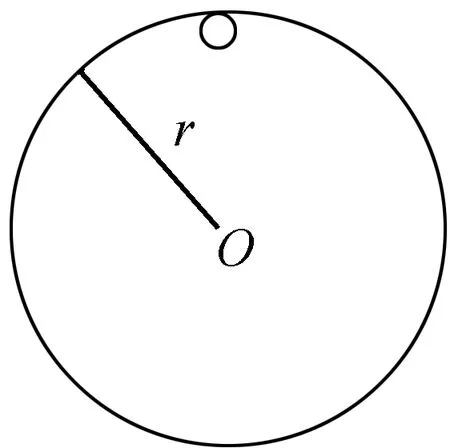
圖2

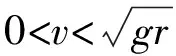
圖3

處于關聯結構水平的學生在教師的幫助下，不僅能正確建構物理模型,還能發現單軌道模型只適用于繩拉球的情況,管道模型也可應用于桿拉或壓球的情況,能舉一反三,朝更高水平層次發展。

2.5 拓展抽象水平

拓展抽象水平是學生思維發展的最高層次,學生能夠將復雜的實際問題轉化為物理模型,能提出自己的觀點。例如在上述例題中,小球在圓軌道上升或者下降時,學生就會產生疑問:既然向心力只能改變線速度的方向,那么又是什么力改變了線速度的大小呢?

學生提出的問題涉及物體在切向方向所受的合外力和切向加速度,雖然高中物理教學對這一知識點沒有作要求,但是對于處在拓展抽象水平的學生,教師卻可以以此為契機,引導學生更深入地理解變速圓周運動。如圖4所示,當小球向上運動到圓弧的D點時,受到軌道的支持力N和重力mg,根據力的平行四邊形定則,可以得到結論：合外力F合并不指向圓心。此時引導學生將F合正交分解,得到指向圓心的力F向和與圓周相切的力F切(圖5),不難發現F向為向心力,F切產生了切向加速度。當F切與線速度方向相反,該力將使小球減速上升。教師還可以讓學生自行分析小球沿圓弧向下的運動,從而深入理解切向加速度,解決學生內心的困惑。

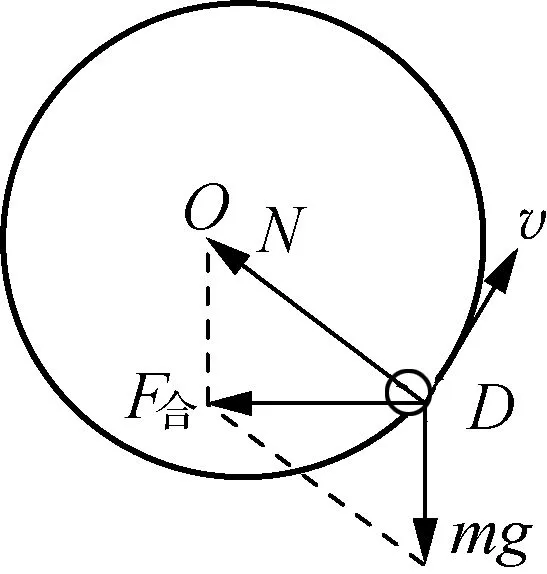
圖4

圖5

處于拓展抽象水平的學生對物理學習有較大的興趣,教師可對這些學生提出更高的要求,如參加物理競賽。在實踐操作中,將處于該水平的學生組班上課,由經驗豐富、專業知識扎實的教師團隊給他們上課,拓展物理教學的層次,例如在變速圓周運動的教學中向學生深入介紹切向加速度的求解及應用等。

3 結語

筆者以SOLO分類理論為指導,以“圓周運動”的復習課為例,對學生的學習水平進行了分析,并將該理論用于教學，初步的教學實踐表明：將SOLO分類理論應用于高中物理復習教學是可行的。