光子糾纏光纖陀螺儀的相位檢測靈敏度分析

張桂才，馮 菁，馬 林，王周祥

（天津航海儀器研究所，天津 300131）

基于Sagnac效應(yīng)的光纖陀螺儀在慣性導(dǎo)航、控制和測量領(lǐng)域已經(jīng)得到廣泛應(yīng)用。在傳統(tǒng)光纖陀螺中，光按經(jīng)典場處理，但探測過程被量子化，具有一種統(tǒng)計特征，被探測的光子數(shù)M服從泊松統(tǒng)計，光子數(shù)的標準偏差其中記為探測的平均光子數(shù)。換句話說，傳統(tǒng)光纖陀螺的相位檢測靈敏度受相對不確定性的影響，稱為散粒噪聲極限[1]。另一方面，作為一種角速率敏感器件，光纖陀螺的精度由相位響應(yīng)以及最小相位分辨率 Δφ共同確定。相位響應(yīng)也即Sagnac標度因數(shù)，正比于兩束反向傳播光波包圍的面積，反比于干涉光波的波長λ。因此增加光纖線圈的長度和直徑，或者采用較短波長可以增強光纖陀螺的精度。X射線以及電子、中子和原子的德布羅意波雖具有較短的波長，但波的產(chǎn)生和傳導(dǎo)相當困難且閉合面積小，不具有精度優(yōu)勢[2]。因此傳統(tǒng)光纖陀螺通常需要采用較大的結(jié)構(gòu)尺寸和光纖長度來進一步提高精度[3-5]。

光子糾纏光纖陀螺儀提供了一種新的技術(shù)途徑，可以突破經(jīng)典Sagnac干涉儀的散粒噪聲極限[2,6,7]。基于光子糾纏的光纖陀螺儀理論上能夠較容易實現(xiàn)超相位分辨率（干涉條紋加倍），但能否實現(xiàn)量子增強的相位敏感，還要依賴于其干涉輸出的相位不確定性是否突破經(jīng)典光纖陀螺儀的標準量子極限，也即超相位檢測靈敏度。光子糾纏干涉測量技術(shù)采用光的非經(jīng)典態(tài)，一般由自發(fā)參量向下轉(zhuǎn)換（SPDC）過程產(chǎn)生[8]。本文闡述了光子糾纏光纖陀螺儀的工作原理，針對量子輸入通常需要雙輸入/雙輸出的光路特征，提出了一種采用雙環(huán)行器的光子糾纏光纖陀螺結(jié)構(gòu)；基于理想的最大光路糾纏N00N態(tài)，首次推導(dǎo)了N00N態(tài)光子糾纏光纖陀螺的德布羅意波的量子干涉公式，并將N00N態(tài)光子糾纏光纖陀螺儀的相位檢測靈敏度極限與具有相同光子數(shù)（光功率）的一般光子數(shù)態(tài)輸入以及經(jīng)典輸入的相位檢測靈敏度進行了對比。

1 采用經(jīng)典和量子輸入的Sagnac干涉儀

1.1 經(jīng)典輸入

圖1 是傳統(tǒng)Sagnac光纖干涉儀的結(jié)構(gòu)示意圖，由一個50：50分束器和一個光纖線圈組成。理想情況下，端口1和端口2的光強測量分別變?yōu)椋?/p>

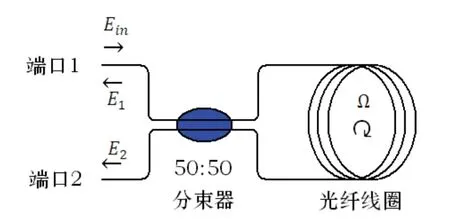
圖1 Sagnac光纖干涉儀Fig.1 Sagnacfiber opticinterferometry

式中,Ein是輸入光場的振幅，E1、E2是兩個輸出光場，φ是旋轉(zhuǎn)引起的Sagnac相移。可以看出，在經(jīng)典理論中，Sagnac干涉儀只需要一個光源，光源發(fā)射的光經(jīng)分束器的其中一個輸入端口分成兩束入射進Sagnac干涉儀，在干涉儀內(nèi)沿相反方向傳播一周后，在同一個分束器上合光干涉，干涉光波也為兩束，一束經(jīng)光源輸入端口輸出，該端口稱為互易性端口（端口1），另一束經(jīng)分束器的另一個輸入端口輸出，該端口稱為非互易性端口（端口2）。對經(jīng)典Sagnac干涉儀來說，非互易性端口對環(huán)境變化敏感，不能精確測量Sagnac相移[1]，所以傳統(tǒng)光纖陀螺采用一種最小互易性光路結(jié)構(gòu)，其輸入/輸出共用一個端口（端口1）。

1.2 量子輸入

在量子理論中，真空場總是存在的。因而，即使沒有場入射進分束器的另一個端口，真空場也從這個端口進入[9]。實際中，為了實現(xiàn)輸入模式和輸出模式的有效分離，我們提出了一種采用雙環(huán)行器的Sagnac干涉儀結(jié)構(gòu)，如圖2所示。a1和a2記為輸入模式的算符。輸出模式b1和b2與輸入模式通過式(2)相關(guān)聯(lián)[2]：

圖2 采用雙環(huán)行器有效分離輸入模式和輸出模式的量子Sagnac干涉儀Fig.2 Quantum Sagnacfiber opticinterferometry withtwocirculators tosplit input/output modes

式(2)中兩個分束器代表了實際分束器的兩次運用。不考慮分束器、光纖線圈的損耗等因素，矩陣SBS、Sφ以及S均為幺正矩陣。輸入和輸出模式通過線性變換相互關(guān)聯(lián)：

其中，系數(shù)Sij的矩陣S被稱為與網(wǎng)絡(luò)有關(guān)的散射矩陣。設(shè)Sagnac干涉儀的散射矩陣S對應(yīng)的幺正算符為U，作用于態(tài)矢量上，使態(tài)矢量演變。利用算符的動力學(xué)性質(zhì)，有：

利用式(4)以及U的幺正性質(zhì)：

因而得到：

式(7)表示輸入光子態(tài)ai經(jīng)過Sagnac干涉儀的演變，式(6)可以由輸出光子態(tài)bi逆演變得到輸入光子態(tài)ai。實際中，上述兩式適合任何幺正性質(zhì)的演變算符U，如UBS（分束器）、Uφ（相移器）。

2 基于N00N態(tài)的光子糾纏光纖陀螺儀

2.1 N00N態(tài)光子糾纏光纖陀螺的輸出態(tài)

由于N00N態(tài)不是Sagnac干涉儀的輸入態(tài)，這里假定非經(jīng)典光源產(chǎn)生的適當光子態(tài)組合第一次經(jīng)過分束器后生成N00N態(tài)，進而在Sagnac干涉儀產(chǎn)生的態(tài)為：

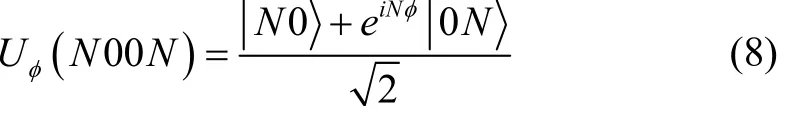
則第二次經(jīng)過分束器后的輸出態(tài)為：

由式(10)可以計算出探測器1和探測器2的輸出光強為：

2.2 二階符合計數(shù)和相位檢測相對不確定性

由式(9)可知，N00N態(tài)光子糾纏光纖陀螺的輸出態(tài)的二階符合計數(shù)I12為：

光子數(shù)N為偶數(shù)時，由式(10)和式(12)推導(dǎo)得到：

分析式(12)(13)發(fā)現(xiàn)，在二階符合計數(shù)I12中，n為偶數(shù)的光子數(shù)態(tài)的二階符合計數(shù)疊加I12-e和n為奇數(shù)的光子數(shù)態(tài)的二階符合計數(shù)疊加I12-o，兩者幅值相同。I12-e和I12-o均呈現(xiàn)N倍頻干涉條紋，且形成互補，這說明I12-e和I12-o都具有完整的量子增強信息。但總的I12=I12-e+I12-o為常值，并不包含Nφ信息。這需要設(shè)計N00N態(tài)光子糾纏光纖陀螺的符合計數(shù)比較方案，獨立獲得完整的二階符合計數(shù)疊加I12-e或I12-o，才能實現(xiàn)海森堡極限的相位檢測靈敏度。探測器1和探測器2的二階符合計數(shù)（I12）減去獨立計數(shù)（I1?I2），并用每個探測器的獨立計數(shù)歸一化，得到為：

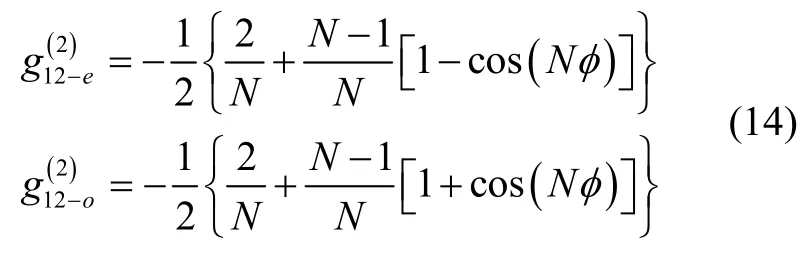
這是與式(1)經(jīng)典干涉輸出對應(yīng)的體現(xiàn)德布羅意粒子的量子干涉輸出公式。其中：

由式(1)和式(14)，綜合考慮散粒噪聲和光子糾纏效應(yīng)，具有相同輸入光子數(shù)N的N00N態(tài)光子糾纏光纖陀螺和經(jīng)典光纖陀螺的相位檢測相對不確定性為：

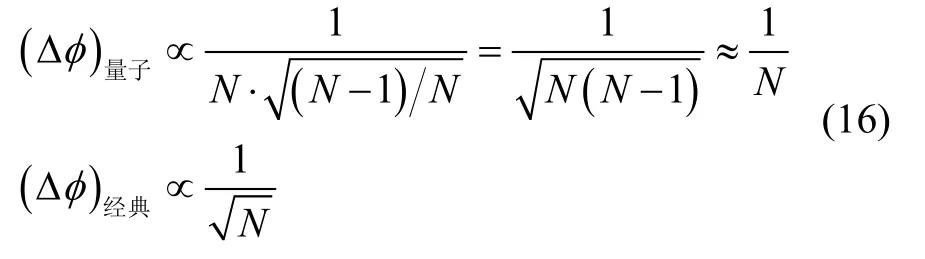
N較大時，N-1≈N，N00N態(tài)光子糾纏光纖陀螺的精度是經(jīng)典光纖陀螺的倍，達到理想的海森堡極限1/N。

3 對比和仿真

3.1 N00N態(tài)與一般光子數(shù)態(tài)的比較

將具有相同光功率（相同光子數(shù)）的N00N態(tài)與一般光子態(tài)輸入進行比較。取N=4，輸入光子數(shù)態(tài)經(jīng)過Sagnac干涉儀的輸出態(tài)為：

其中，

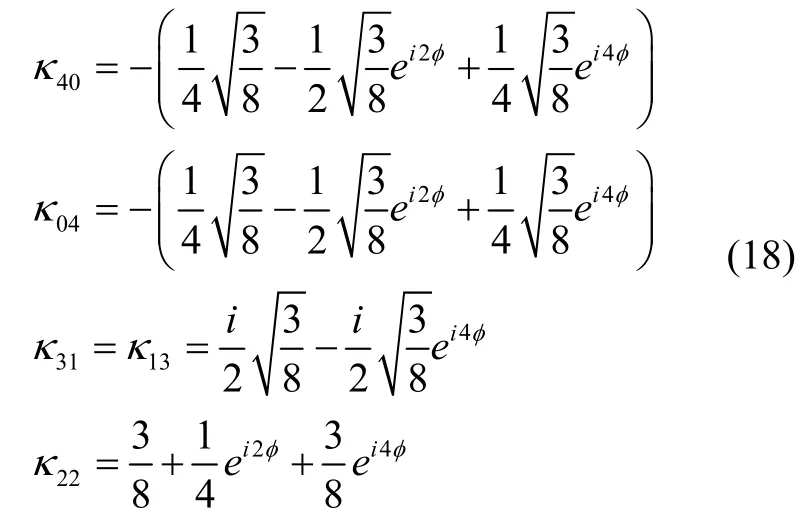
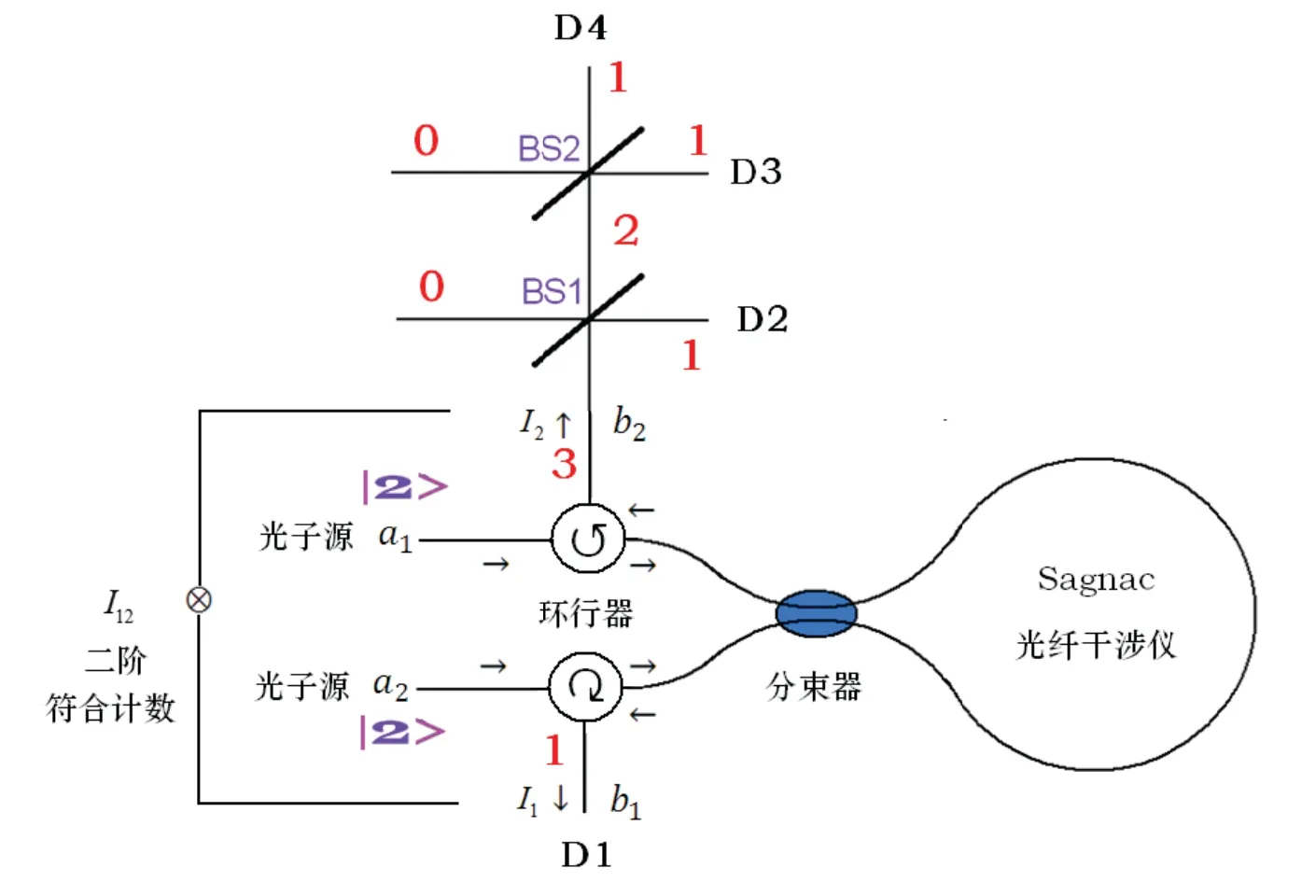
圖3 采用四個單光子探測器Di （i=1,2,3,4）對輸入態(tài)為的輸出態(tài)進行高階符合計數(shù)Fig.3 Using four single-photon detectors tomeasure higher order coincidences for input states

3.2 N00N 態(tài)和其它輸入態(tài)的相位檢測靈敏度

由式(1)(14)(20)(21)可以給出具有相同光子數(shù)（N=4）的經(jīng)典態(tài)、4004態(tài)、輸入態(tài)的二階符合計數(shù)以及高階符合計數(shù)的干涉響應(yīng)曲線，如圖4所示。可以看出，經(jīng)典態(tài)只有一個干涉條紋，幅值為4；4004態(tài)有四個干涉條紋，幅值為輸入態(tài)的二階符合計數(shù)有兩個干涉條紋，幅值也為34；輸入態(tài)的高階符合計數(shù)有四個干涉條紋，但幅值僅為2×（3/16）2。

圖4 具有相同光子數(shù)（N=4）的經(jīng)典和量子的干涉響應(yīng)曲線Fig.4 Classical and quantum interferenceresponse curves with the samephoton number (N=4)

如前所述，光纖陀螺作為一種角速率敏感器件，其精度由相位響應(yīng)Nφ也即Sagnac標度因數(shù)以及最小相位分辨率Δφ共同確定。根據(jù)文獻[7]的定義，干涉條紋倍頻或?qū)е驴s短的德布羅意波長，稱為超相位分辨率；突破散粒噪聲極限，稱為超相位靈敏度。表1給出了經(jīng)典干涉和N00N態(tài)、一般光子數(shù)態(tài)（）的量子干涉得到的相位檢測靈敏度對比。可以看出，N00N態(tài)作為最大光路糾纏態(tài)，已經(jīng)突破散粒噪聲極限，達到海森堡極限，比散粒噪聲極限低倍（N=4）；而一般光子數(shù)態(tài)的二階符合計數(shù)雖然存在2φ信息，但因為并非所有的輸出態(tài)都對二階符合計數(shù)有貢獻，存在一個固有效率或概率，未突破散粒噪聲極限；由于類似的原因，輸入態(tài)的四階符合計數(shù)盡管實現(xiàn)了干涉條紋的4倍頻，但其概率（強度）進一步降低，其相位檢測靈敏度比經(jīng)典干涉低得多。

表1 經(jīng)典態(tài)與非經(jīng)典態(tài)的相位檢測靈敏度對比（ N=4）Tab.1 Comparison of classic state with non-classic states for phase sensitivity

4 結(jié) 論

基于N00N態(tài)的光子糾纏光纖陀螺儀的雙輸入/雙輸出特征，提出了一種采用雙環(huán)行器的光子糾纏光纖陀螺光路結(jié)構(gòu)，首次推導(dǎo)了N00N態(tài)光子糾纏光纖陀螺的德布羅意波的量子干涉公式，并對光子糾纏光纖陀螺的相位檢測靈敏度進行了研究。分析表明，采用最大路徑糾纏N00N態(tài)，基于被探測的N光子的糾纏特性，導(dǎo)致一種縮短的德布羅意波長這種德布羅意粒子的統(tǒng)計特征服從亞泊松分布，探測的不確定性由經(jīng)典的降為同時，光子糾纏效應(yīng)使二階干涉條紋的頻率提高了N倍，這導(dǎo)致比經(jīng)典光纖陀螺增強了倍，可以突破散粒噪聲極限而達到海森堡極限。盡管N00N態(tài)的制備目前還相當困難，但國外的研究仍非常活躍[10-12]，其在光子糾纏光纖陀螺儀方面具有潛在的應(yīng)用前景。將N00N態(tài)與具有相同光子數(shù)（光功率）的一般光子數(shù)態(tài)（的量子干涉以及經(jīng)典干涉的相位檢測靈敏度進行了對比。其它非經(jīng)典態(tài)由于輸出態(tài)的二階符合計數(shù)及高階符合計數(shù)存在一個固有效率，可能很難突破散粒噪聲極限。此外，光子糾纏光纖陀螺儀還涉及光路互易性、施加偏置調(diào)制、光路元件不理想引起的退相干等問題，有待進一步研究。