多機移動條件下飛行甲板路徑規劃研究*

（海軍航空大學青島校區 青島 266041）

1 引言

艦載機在航母甲板的移動是航母安全作業的重要隱患，其移動效率也制約著航母戰斗力的生成。由于航母飛行甲板與機庫甲板的高度復用性，艦載機在甲板的調運路徑應進行合理規劃，避免碰撞的同時提高轉運效率，這也是實現艦載機自動牽引的核心問題。

路徑規劃問題較早應用于自主移動機器人［1～3］，通過自動推理、全局規劃、移動控制等過程，實現機器人的自主導航移動。在艦載機應用方面，劉亞杰等［4］針對艦載機轉運過程中的碰撞問題，采用柵格法表示艦載機位置信息，檢測路徑是否安全，其轉運路徑需要人工設置。高杰等［5］針對航母甲板艦載機調運過程問題，采用混合整數規劃方法對移動路徑優化，采用“碰撞區域”方法評價路徑合理性，從而生成所需路徑。張競等［6］著力解決甲板環境下的艦載機路徑規劃問題，主要針對艦載機在牽引模式下，整個運動系統的路徑優化。本文考慮到航母飛行甲板與機庫甲板通常配備多個轉運小組，采用新的碰撞檢測方法，研究多機轉運條件下的飛行甲板路徑規劃問題。

2 艦載機飛行甲板路徑規劃建模

2.1 艦載機轉運過程描述

在航母甲板轉運過程中，當確定了艦載機的初始停機位和目標停機位后，我們應能夠按照一定的轉運原則，使整個轉運過程用時最短，如果是多機轉運，則應按照最后一架飛機到達目標停機位的時間作為最終用時，其具體過程如圖1所示。

圖1 雙機甲板轉運路徑

圖1中A1與A2為初始艦載機停機位，A3與A4分別是前兩飛機的目標停機位。B1與B2為障礙機位，陰影部分為障礙建筑。整個轉運過程應從離開初始機位開始計時，到最后一個到達目標機位的艦載機為止結束計時。每一架飛機可以有任意種行走路線，圖中只列出其中四條轉運路線，可以明顯看出，轉運路線重復度高。當只有單架飛機轉運時，只需考慮障礙物的避碰就可以，因此最短路徑即為用時最少的路徑。但多架飛機轉運時，我們需要綜合考慮避碰、等待用時等因素，這時不能以路徑長短作為最優參考路線，應該以作業時間長短作為參考指標［7～8］。

2.2 路徑規劃建模

根據上述作業流程分析，可以將艦載機甲板移動過程描述為求解帶有約束條件的飛機甲板轉運用時計算問題。針對飛行甲板多機轉運任務建模，為保證模型可行性，應進行如下前提假設：

1）牽引作業移動速度勻速恒定，不超過安全限速。

2）牽引作業轉彎時，按設計角度自行轉彎，不超過安全角度。

3）牽引進入停機位一次成功，不計算調整時間。

其表達式如下所示：

式（1）中n為每套轉運方案的路徑數量，m為每次轉運的艦載機數量，T（i）表示每段轉運路徑所用時間，表達式含義為求各轉運方案中用時最少的方案；式（2）中L為最大艦載機的最大尺寸，k為每套方案中的艦載機初始機位與目標機位的總數量，Ai表示第i架艦載機的位置，表達式含義為所有初始機位與目標機位不干涉，相距一個機位以上；式（3）中m'表示障礙飛機數量，n表示轉運路徑數量，Si表示第i條轉運路徑，Bj表示第j架障礙飛機位置，表達式含義為轉運路線與障礙飛機不相交；式（4）中n表示轉運方案的路徑數量，IL表示障礙建筑，DA表示甲板邊緣，表達式含義為艦載機轉運空間在甲板內部，且不占用建筑空間；式（5）中m表示每次轉運的艦載機序列，n'表示同一架飛機的轉運序列，S（i）表示第i條轉運路徑，表達式含義為對于同一架飛機的任意轉運路徑不相交；式（6）中t表示轉運時間軸，n表示轉運路徑數量，Si（t）表示第Si條路徑在t時刻的位置，表達式含義為任意艦載機在相同時刻的位置不同。

3 艦載機碰撞及等待計算

3.1 艦載機碰撞問題計算

艦載機在甲板的水平移動，考慮到轉運作業的安全性問題，是不允許高低裝備之間相互穿插經過的，所以，其整個移動碰撞問題可以理解為二維平面內的碰撞檢測。目前平面碰撞檢測方法主要采用“柵格法”和“包圍盒法”。本文采用多邊形包圍盒法來近似描述艦載機輪廓，將預選的艦載機路徑與包圍盒相交測試，實現路徑的避碰。

對于甲板面的艦載機，如圖2所示，可以采用圖3的多邊形包圍盒，艦載機直升機采用圖4的多邊形包圍盒，其數學表達式可采用邊序列的表達方法，分別為

圖2 艦載機輪廓

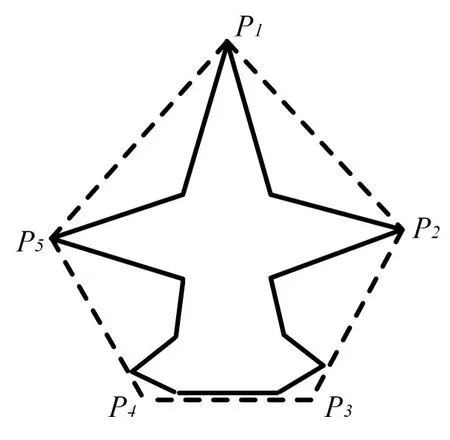
圖3 多邊形包圍盒

圖4 直升機多邊形包圍盒

對于移動路徑與包圍盒的相交測試，可以采用多邊形徑向膨脹法。由于艦載機多邊形包圍盒是規則五邊形，當包圍盒沿預定路徑移動時，其多邊形的中軸線一定與路徑重合，這時若移動多邊形包圍盒與障礙物多邊形包圍盒相撞，則其中軸線與障礙物多邊形必定相交，也就是說預定路徑與障礙物多邊形各邊的距離小于移動艦載機多邊形的法向寬度，其檢測過程如圖5所示.

碰撞檢測具體計算步驟可分為如下四步：

1）計算移動艦載機多邊形法向寬度r，同時設置艦載機之間安全距離θ；

2）將障礙飛機各邊向外平移r+θ，得到新的多邊形q'；

3）將移動艦載機路徑序列分別與q'的各邊進行相交檢測，如果任意一對邊相交，將目標函數適應度值設為最大，循環跳出；

4）如果第3）步中各邊全不相交，則進入下一障礙飛機的碰撞循環，重復1）～3）步驟。

3.2 艦載機碰撞等待計算

以上是對甲板固定障礙物的碰撞計算，其采取的策略為“繞行”方式，發生碰撞即排除路徑。對于多機移動的碰撞問題，需要加入等待時間的計算。當兩架飛機同時在甲板移動時，一方面需要避碰固定障礙物，另一方面需要相互避碰，這時應以總移動時間最短為目標，比較繞行所需時間與等待所需時間哪個更少，則采取哪種行走策略，其過程如圖6所示。

圖6 雙機路徑選擇策略

A1和A2分別為初始停機位，A3和A4分別為前兩飛機的目標停機位，B1為障礙飛機。選取S1為A1飛機的轉運路徑，選取S2和S3為目標飛機的轉運路徑。當A2飛機沿S2路徑移動時，移動距離短，但需要等待A1飛機通過后才能繼續前進，而沿S3路徑移動時，移動距離長，但無需等待。

本文采用“離散路徑、近距優先”的策略處理多機移動問題，一是在所有預選艦載機路徑中設置兩個轉折點，各轉折點間采用直線路徑，在艦載機進入每一段路徑前，先判斷該路徑碰撞情況再駛入，這樣可以減少總的路徑等待時間；二是按照預選路徑最短的原則，將艦載機移動順序進行排列，賦予艦載機行動優先級，這樣可以避免艦載機的重復等待。移動艦載機之間的碰撞檢測計算按以下步驟計算：

1）依次存儲各飛機轉運路徑序列Sn，同時，為各飛機建立等待時間序列Tn，Sn與Tn應該一一對應。

2）根據預選路徑長度，計算各艦載機轉運優先級。

3）判斷當前待轉運艦載機優先級Ω，若Ω=1則無需進行等待時間計算，轉入第7）步。

4）依次將本優先級艦載機各路徑與Ω優先級以前的艦載機所有路徑進行相交判斷。

5）若在SΩ(i)路徑相交，則計算該優先級以前艦載機經過該路徑的時間t，同時計算Ω優先級艦載機經過SΩ(i-1)路徑的時間t'，t-t'即為SΩ(i)的路徑等待時間，計入TΩ，轉入第7）步。

6）若在SΩ(i)無相交情況，記錄SΩ(i)的路徑等待時間為0，計入TΩ，轉入第7）步。

7）計算SΩ優先級艦載機轉運時間，同時加入等待時間TΩ。

8）轉第3）步計算下一優先級艦載機轉運時間。

4 艦載機路徑規劃計算

在艦載機初始位置與目標位置確定的情況下，每架艦載機路徑選取兩個中間轉折點，轉折點間采取直線路徑的方式，則n架艦載機的路徑規劃問題就轉變為n×2個路徑點的組合優化問題。本文采用離散粒子群算法解決該問題［9～11］。該算法在多維空間多峰問題尋優、動態目標尋優及排列組合優化等方面有著速度快、解質量高、魯棒性好等優點。

4.1 粒子編碼

在離散粒子群算法中，我們將每一套路徑方案編碼為一個粒子，通過多個粒子之間不斷競爭，追逐最優粒子，達到尋找最優方案的目的。每一個粒子的維度由艦載機的數量和中間轉折點的數量決定，每一個中間轉折點采用二維坐標(x，y)表示，則對于n架艦載機和2個中間轉折點的路徑方案，其每一個粒子編碼可采用n×4維矩陣表示。

4.2 算法步驟

設置算法種群數量為D，最大迭代次數為N，對于4.1節中的編碼方式，其算法描述如下：

1）算法初始化。設置初始種群，隨機設置D個粒子的初始位置，初始速度。

2）針對初始種群，對粒子解碼，采用第2節中的模型及第3節中的計算方法計算適應度值，確定歷史最優粒子，全局最優粒子。

3）采用式（9）計算粒子速度，如果速度超過最大值，則取為最大值。

4）根據第3）步中的粒子速度，采用式（10）計算粒子位置，如果超過最大值，按照碰撞處理。

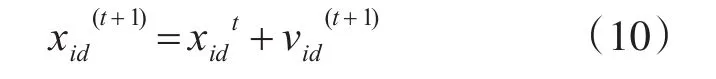
5）針對更新后的粒子，采用第2節中的模型及第3節中的計算方法計算適應度值，更新歷史最優粒子，全局最優粒子。

6）判斷是否達到迭代次數N。如果達到，輸出計算結果；否則，轉向步驟3）。

4.3 參數設置

設置種群數量D為50，確保隨機采樣率。設置最大迭代次數為100，后期根據迭代結果情況再調整。w為慣性權重，較大的w值有利于保證算法的全局性，較小的w值有利于保證算法的收斂性。本文采用動態慣性權重方式，前期具有較寬的搜索能力，后期具有較精確的尋優能力［12］，如式（10）所示。

式中t表示迭代次數，wmax取為1，wmin取為0.2。c1和c2為學習因子，c1表示向自身歷史最優粒子靠近的權重，c2表示向全局最優粒子靠近的權重，本文取c1為1.7，c2為1.9，保證算法全局性較高。

4.4 計算結果

采用Matlab7.1編程，利用圖1中的艦載機布列任務進行測試，飛機轉運速度按照4km/h計算，甲板總尺寸按照300m×70m計算，其所有飛機的坐標及機頭角信息如表1所示。

表1 飛機坐標與機頭角信息

計算結果如下：

1）連續優化十次，十次最優路線如圖7所示，圖中障礙物飛機周圍虛線為按照3.1節中碰撞檢測方法外擴后的輪廓線，由于機頭頂點外擴距離過遠，本文采用六邊形描述，其外擴方法與前文描述一致。黑色實線為經過十次優化后的路徑，都不與藍色輪廓線相交，結果表明，本文所采用碰撞檢測方法適用于多機甲板轉運要求。

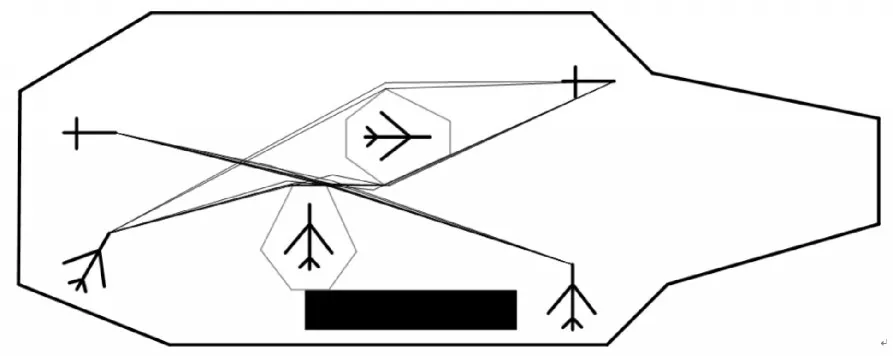
圖7 十次最優的路線

2）連續優化十次，其最終最優方案如圖8所示，十次轉運過程的最優用時與等待時間如表2所示。最終最優路徑行駛總用時為213.3s，其中，行駛等待時間為32.6s。十次最優結果的最大用時為227.2s，平均最優用時為218.5s，結果浮動范圍相差不大。該結果表明，本文所采用碰撞檢測方法及智能算法計算偏差小，全局收斂性好，沒有陷入局部極小，可以用于飛行甲板多機轉運輔助決策。

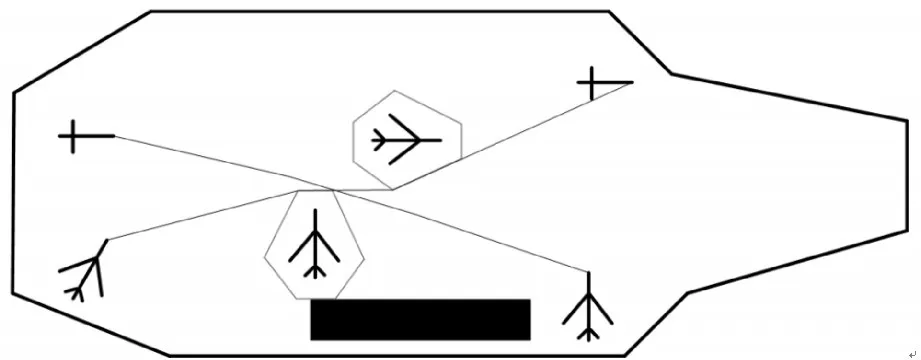
圖8 雙機轉運最優路徑

表2 十次轉運的最優用時與其中等待用時

3）采用50個粒子種群，100次迭代循環，連續優化十次的迭代曲線如圖9所示，所有迭代循環能夠在70～80代之間完成收斂，收斂結果幅度較小。其結果表明，使用離散粒子群算法計算該碰撞檢測問題，算法收斂速度快，收斂一致性好，迭代次數設置符合要求。

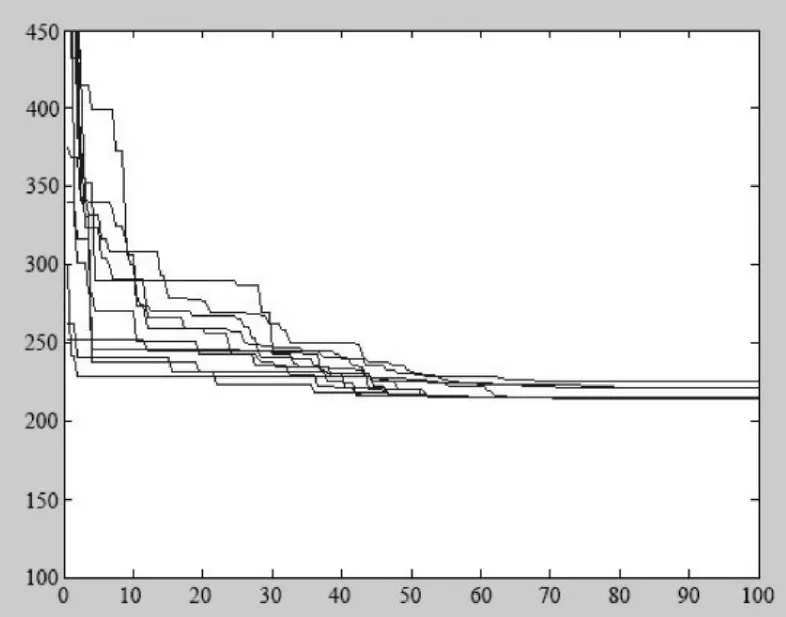
圖9 十次迭代的收斂曲線

5 結語

本文研究了以碰撞等待時間為主要因素的飛機移動碰撞問題，采用離散粒子群算法求解多機轉運條件下的甲板路徑規劃模型。通過對文中實例的驗證，本研究給出的雙機移動路徑能夠有效實現艦載機與固定障礙物的避碰，同時，也能夠實現移動飛機之間的避碰與等待，給出了飛機等待時間。計算結果表明本研究符合實際規劃需求，可以用于艦載機自動牽引的輔助決策。