含空間自回歸誤差的空間自回歸模型的經驗歐氏似然推斷*

唐 潔

（廣西師范大學數(shù)學與統(tǒng)計學院，廣西桂林541004）

0 引言

含空間自回歸誤差的空間自回歸模型(Spatial Autoregressive Model with Spatial Autoregressive Disturbanc?es，簡記為SARAR):

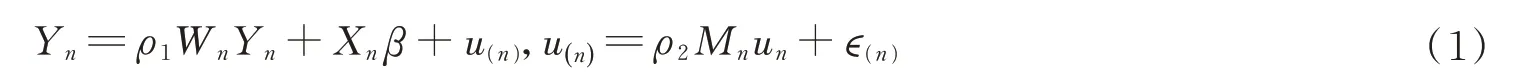
其中，n是空間樣本數(shù)量；ρj,j=1,2 是空間自回歸系數(shù)且|ρj| ＜1,j=1,2；βk×1是相應回歸系數(shù)向量；Xn=(x1,x2,…,xn)′是n×k數(shù)據矩陣,包括k列解釋變量；Yn=(y1,y2,…,yn)′是n×1 維被解釋變量;Wn和Mn是已知的n×n空間權重矩陣（非隨機）；?(n)是空間誤差模型n×1 的誤差向量

SARAR 模型是更一般的空間計量模型，它對存在空間依賴性的數(shù)據有較好的解釋作用，無論是滯后項存在依賴性還是擾動項存在空間依賴性。它將存在空間誤差效應的空間誤差模型(SEM)與空間滯后效應的空間自回歸模型(SAR)結合起來，分別對應于ρ1=0 與ρ2=0 的情形。

經驗似然方法是由Owen 在文獻[1]中提出的一種參數(shù)推斷方法。通過經驗似然方法研究SARAR 模型則是文獻[2]的主要工作。但是經驗似然方法在求解過程中會出現(xiàn)沒有顯示解的情況，且計算復雜。為了解決這些問題，Owen 在文獻[3]中提出用經驗歐氏似然來代替經驗似然。而羅旭在文獻[4]中，就系統(tǒng)地研究了經驗歐氏似然，發(fā)現(xiàn)了可以很好地解決經驗似然中的棘手問題，并且經驗歐氏似然也同樣擁有大樣本性質。基于此，本文通過經驗歐氏似然方法來研究SARAR 模型。

1 主要結果和證明

記An(ρ1) =In-ρ1Wn,Bn(ρ2) =In-ρ2Mn并且假設An(ρ1)和Bn(ρ2)是非奇異矩陣。于是可以得到：

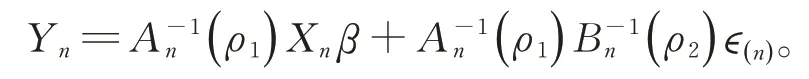
此時，假設?(n)是正態(tài)分布的，則Yn服從期望為An1(ρ1)Xn β，方差為的正態(tài)分布。

于是，Yn的擬似然函數(shù)為：

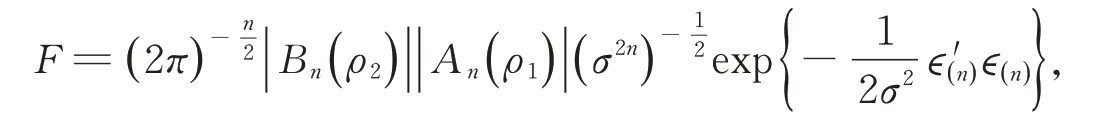
其中?(n)=Bn(ρ2){An(ρ1)Yn-Xn β}。

進而，Yn的擬對數(shù)似然函數(shù)為：

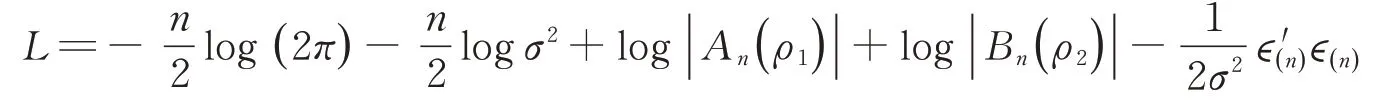
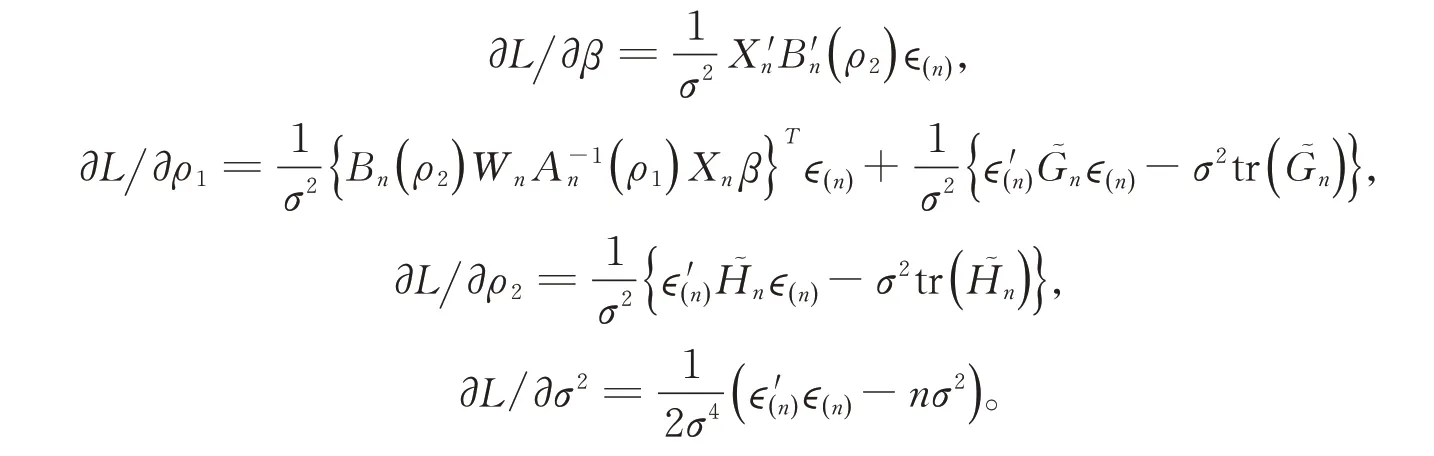
令上述偏導數(shù)等于0，可以獲得以下估計方程：

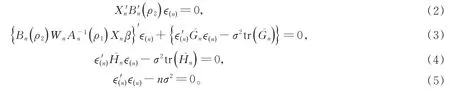
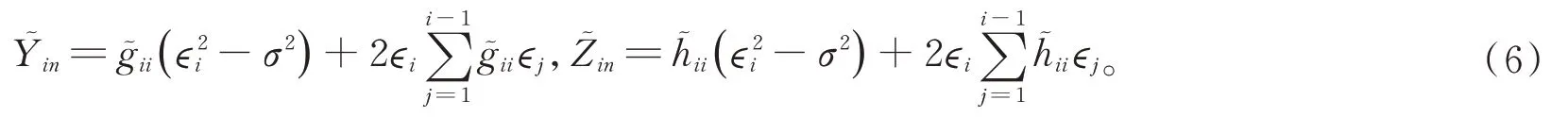
則Fi-1?Fi，是Fi-可測的，并且E(|Fi-1) =0。因此，{,Fi,1≤i≤n}和{,Fi,1≤i≤n}構成兩個鞅差序列，且

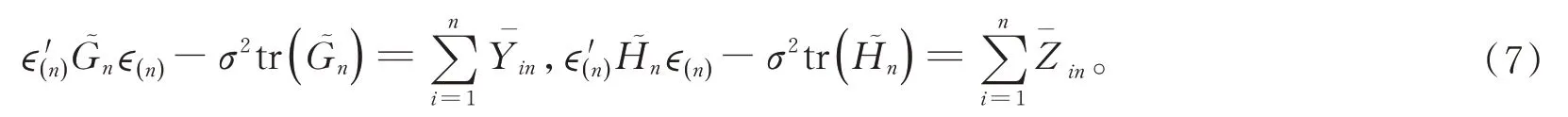
根據(2)到(7)可以得出參數(shù)θ?(β′,ρ1,ρ2,σ2) ∈Rk+3的估計方程，令

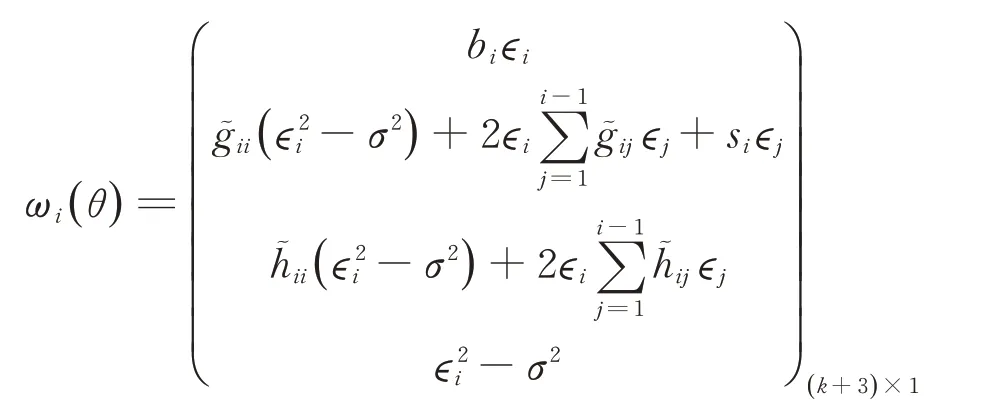
通過ωi(θ)提出θ的經驗歐氏似然比統(tǒng)計量

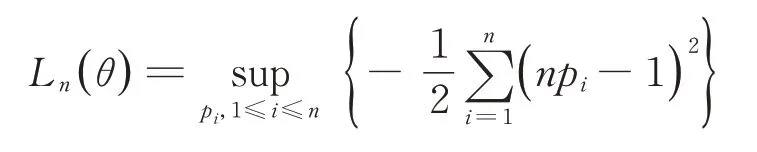
其中，{pi}滿足

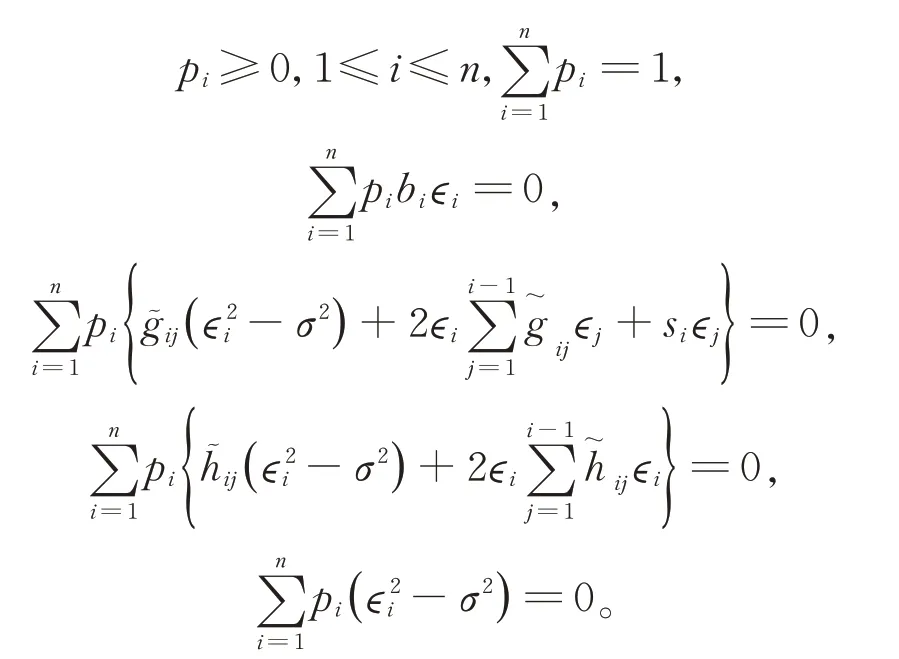
在本文中，記μj=E(?ji),j=3,4，用Vec(diagA)表示由矩陣A的對角線上的元素構成的列向量，用‖a‖表示向量a的第二范數(shù)，用1n表示由1 作為元素組成的n維列向量，為了獲得經驗歐氏似然比統(tǒng)計量的漸近分布，需要給出以下假設條件：

A1.{?i,1≤i≤n}是均值為0，方差有限的獨立同分布隨機變量序列，且存在η1＞0，使E|?1|4+η1＜∞。

A2.假設Wn,Mn,A-1n(ρ1),B-1n(ρ2)及{xi}滿足以下條件：

（i）矩陣Wn，Mn，A-1n(ρ1)，B-1n(ρ2)行元素和列元素的絕對值之和均一致有界；

（ii）{xi}是一致有界的。

A3.存 在常數(shù)cj＞0,j=1,2,使 得0 ＜c1≤λmin(n-1c) ≤λmax(n-1Σk+3) ≤c2＜∞,其 中λmin(A)和λmax(A)分別表示矩陣A的最小和最大的特征值，且

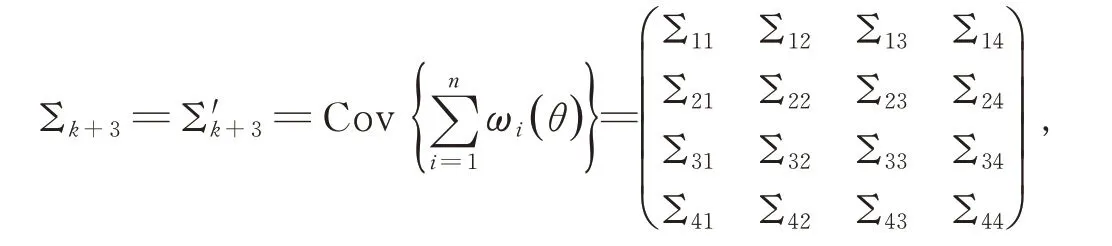
其中，

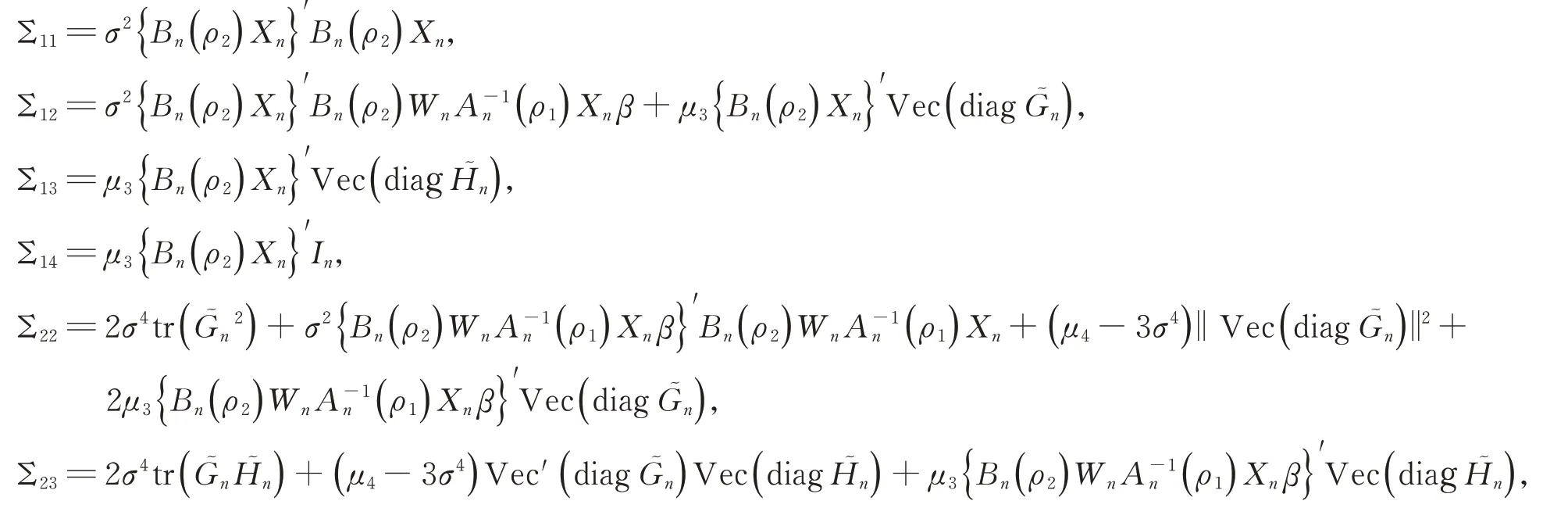
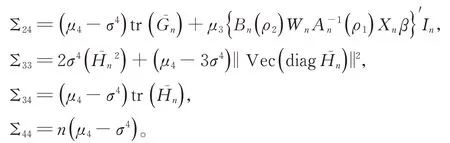
引理1在(A1)～(A3)假設條件下，當n→∞時，有

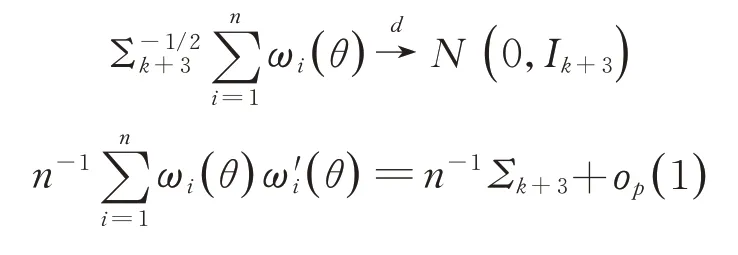
見文獻[4]的引理3。

定理1在(A1)～(A3)假設條件下及模型(1)下，當n→∞時，有-2Ln(θ)→dχ2k+3，其中，表示自由度為k+3 的卡方分布。

證明：SARAR 模型下經驗歐氏（對數(shù)）似然函數(shù)為：

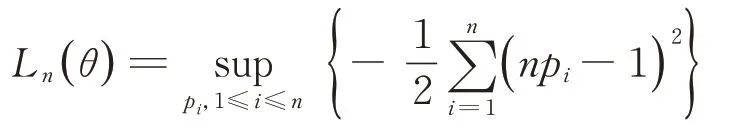
利用拉格朗日乘子法給出Ln(θ)的表達式。為此取

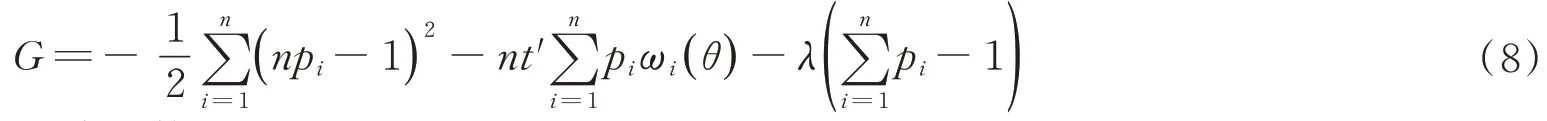
其中t′∈Rk+3。對G求關于pi的偏導數(shù)，得

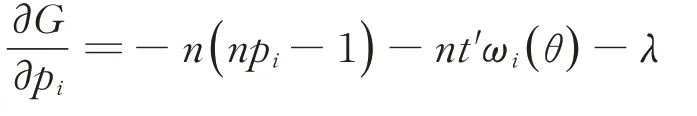
并令

在(9)式兩邊對i從1 加到n求和，得

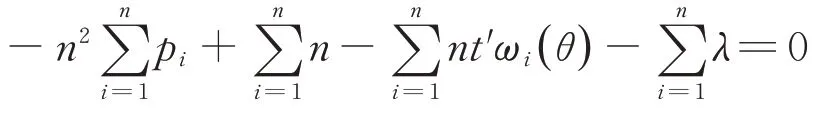
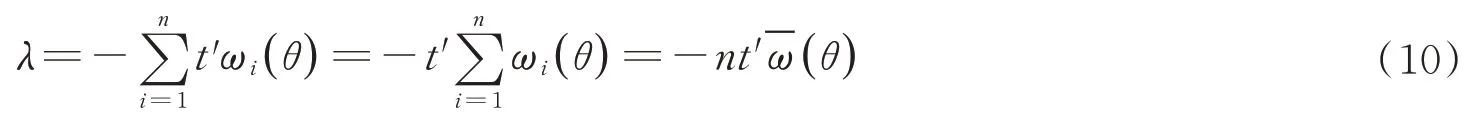
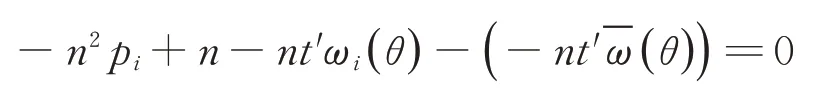
上式化簡可得

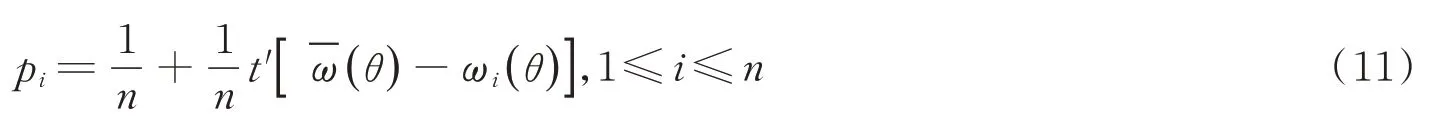
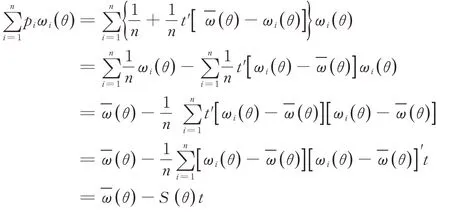
由(10)～(12)可得

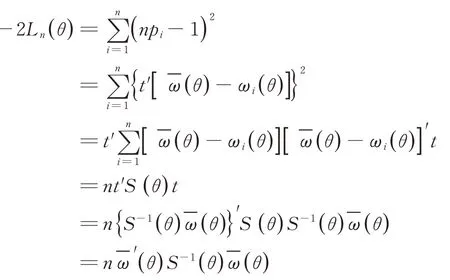
由引理1，得

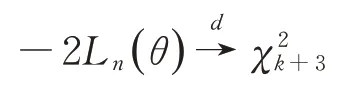
由此完成了定理1 的證明。