移動平均模型的經驗歐氏似然推斷*

容健榮

（廣西師范大學數學與統計學院，廣西桂林541004）

0 引言

移動平均模型是自回歸移動平均模型的一個特例,而自回歸移動平均模型是時間序列分析的一個重要模型。研究移動平均模型可為日后自回歸移動平均模型的研究帶來一定的借鑒。

經驗似然方法是由Owen 在文獻[1]中提出的一種非參數推斷方法。由于它擁有類似于重抽樣方法的優點,吸引了一大批學者投身于經驗似然方法的研究。Li 等人在文獻[2]中利用了經驗似然方法對移動平均模型進行研究。但是經驗似然方法在求解過程中會出現沒有顯式解的情況，而且計算比較復雜。為了應對這些問題,Ow?en 在文獻[3]中提及了使用經驗歐氏似然來替代經驗似然。羅旭在文獻[4]中系統地研究了經驗歐氏似然,發現了經驗歐氏似然方法使得在一些場合下,其解擁有顯式表達式,由此降低了計算上的復雜性,而且經驗歐氏似然方法也同樣擁有類似于經驗似然方法的漸近性質。基于此，本文通過經驗歐氏似然方法來研究移動平均模型。

1 主要結果和證明

考慮下面的移動平均模型：

其中q是模型的階數,而且q是一個正整數,β1,…,βq是模型的參數。{?t}是一個獨立同分布并且具有非退化密度函數的序列,它們的均值為0,方差為σ2。令yn=(x1,…,xn)′,其中{xt}是來自模型(1)的觀測值。記β0=1,β=(β1,…,βq)′,θ=(β′,σ2)′=(θ1,…,θq+1)′。 能 夠 計 算 出E(yn) =0,Σn=Cov(yn) =(Cov(xi,xj))n×n,其中

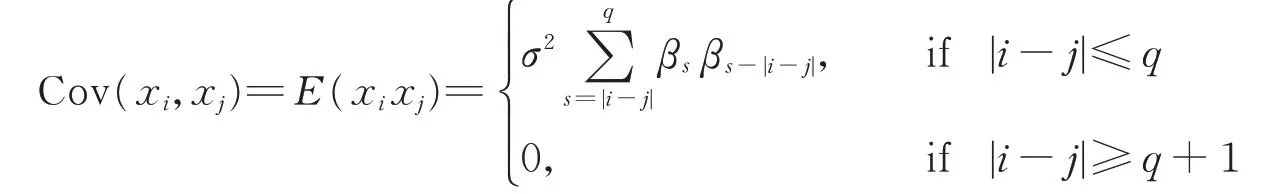
yn的擬對數似然函數(省略常數項)

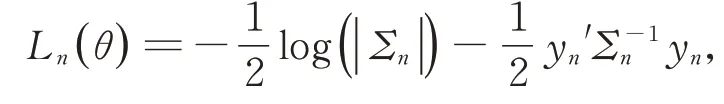
對似然函數求偏導可得

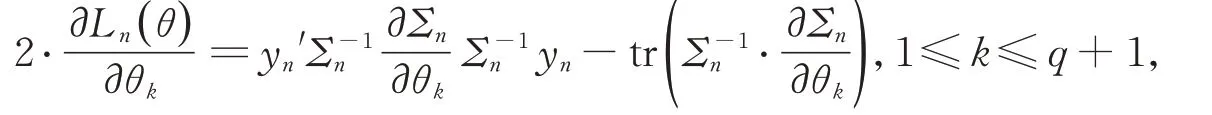
令上述偏導數等于0, 我們獲得以下估計方程：

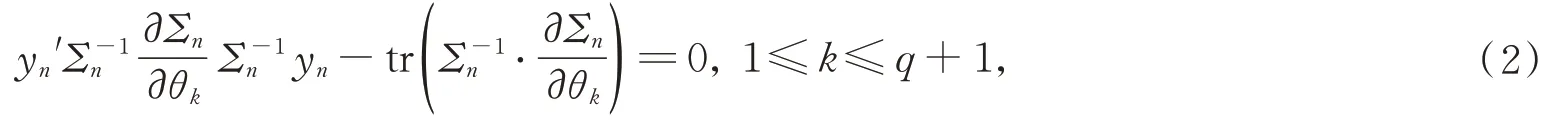
令?(n)=(?1-q,?2-q,…,?n)′,β(i)=(0,…,0,βq,…,β0,0,…,0)′,其中βq是β(i)的第i部分。則xi=,1≤i≤n,可得

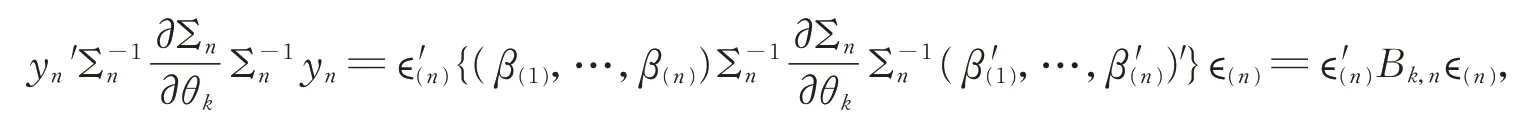
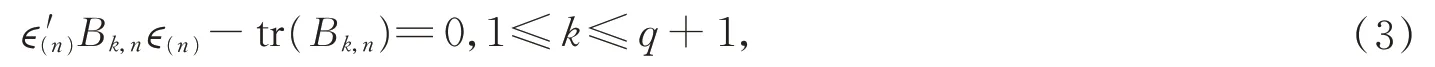
我們用bki,j表示矩陣Bk,n的(i,j)元素。并且規定，當求和的上標小于1 時，我們令該和為0。為了處理(3)式中的二次型形式，需要引入文獻[5]中介紹的鞅差序列。

定義σ-域:F0={φ,Ω},Fi=σ(?1-q,?2-q,…,?i),1-q≤i≤n。令

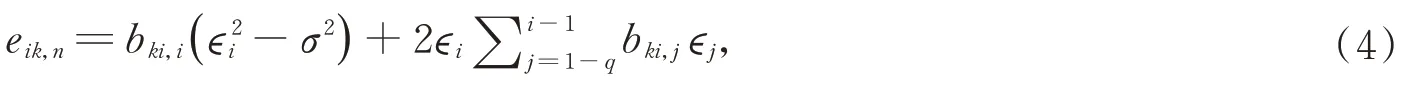
則Fi-1?Fi,eik,n是Fi-可測的，并且E(eik,n|Fi-1)=0。因此{eik,n,Fi,1-q≤i≤n}構成一個鞅差序列，且

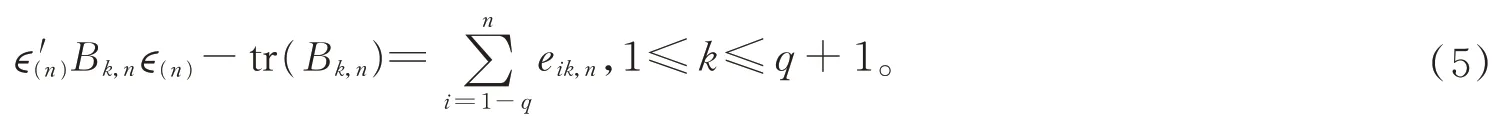
令

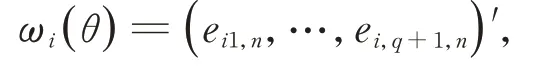
通過ωi(θ),我們提出θ的經驗歐氏似然比統計量

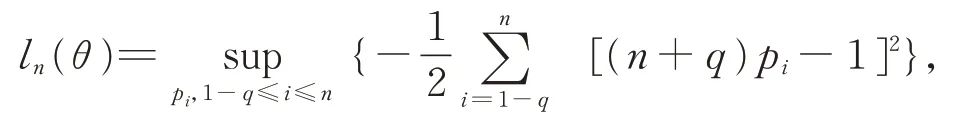
其中pi滿足

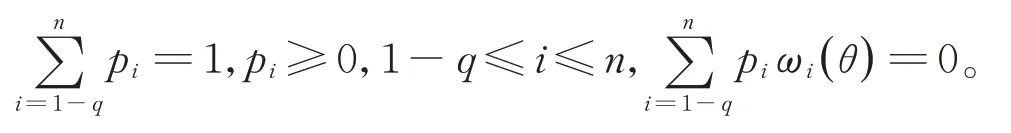
在本文中，記μ4=E?4t。用Vec(diag(A))表示由矩陣A的主對角線上的元素構成的列向量。令ΣSn=2σ4C1+(μ4-3σ4)C2, 其 中C1=(C1i,j),C1i,j=tr(Bin Bjn), 和C2=(C2i,j),C2i,j=(Vec(diag(Bin)))′×(Vec(diag(Bjn)))。為了獲得經驗歐氏似然比統計量的漸近分布，需要給出以下假設條件：

(A1){?i,1-q≤i≤n}是均值為0,方差有限的獨立同分布隨機變量序列,且存在δ＞0,使E|?i|4+δ＜∞。

(A3)存在常數c＞0 使ηmin((n+q)-1ΣSn) ≥c,其中ηmin(A)表示矩陣A的最小特征值。

(A4)移動平均模型的移動平均系數多項式方程的根在單位圓外。

引理1在(A1)～(A3)假設條件下，當n→∞時,有

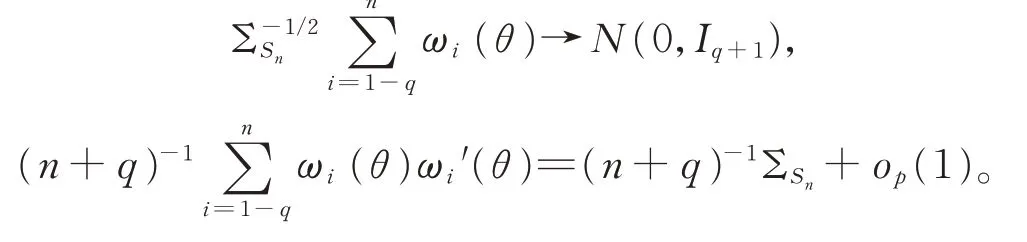
見文獻[2]的引理3。

定理1在(A1)～(A3)假設條件下，當n→∞時,有

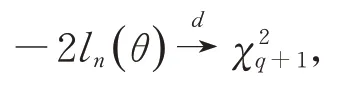
其中表示自由度為q+1 的卡方分布。

證明：利用拉格朗日乘數法給出ln(θ)的表達式,為此取

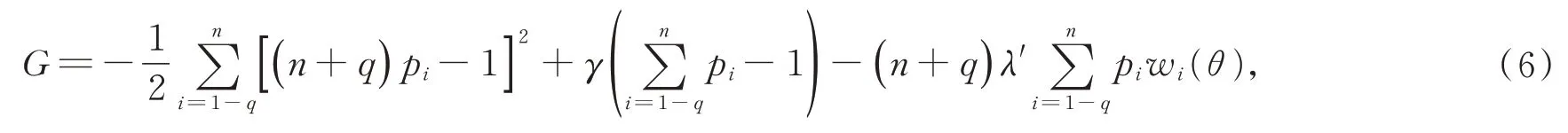
其中γ∈R,λ∈Rq+1是拉格朗日乘數。對(6)式求關于pi的偏導數并令為零,即?G/?pi=0,得

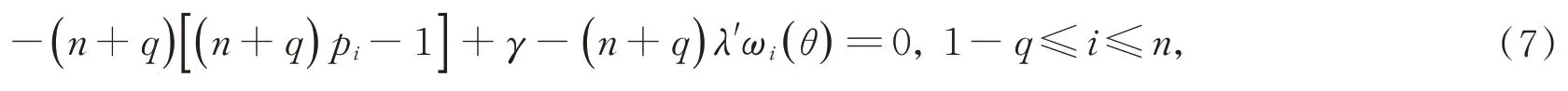
在(7)式兩邊對i從1-q到n求和,得

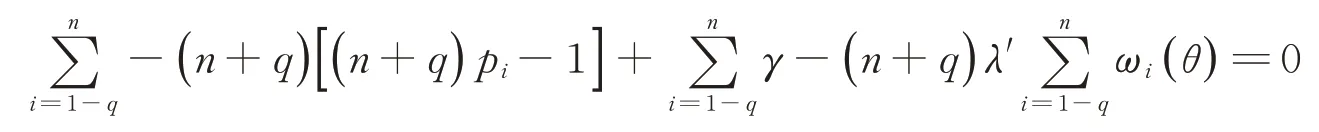
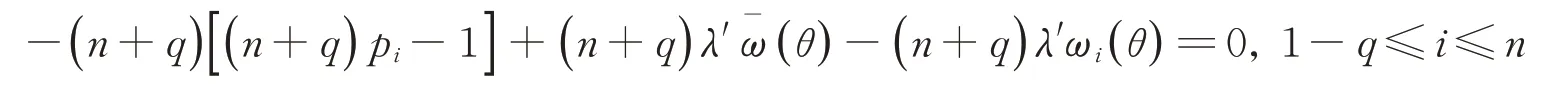
上式化簡可得

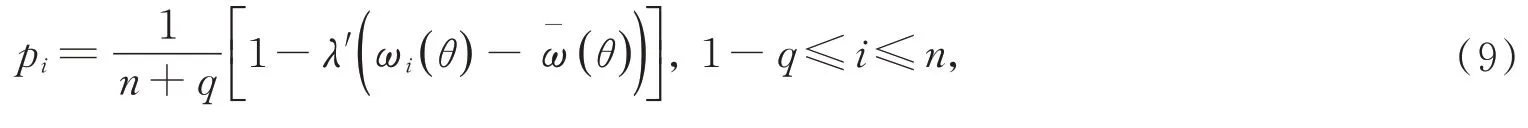
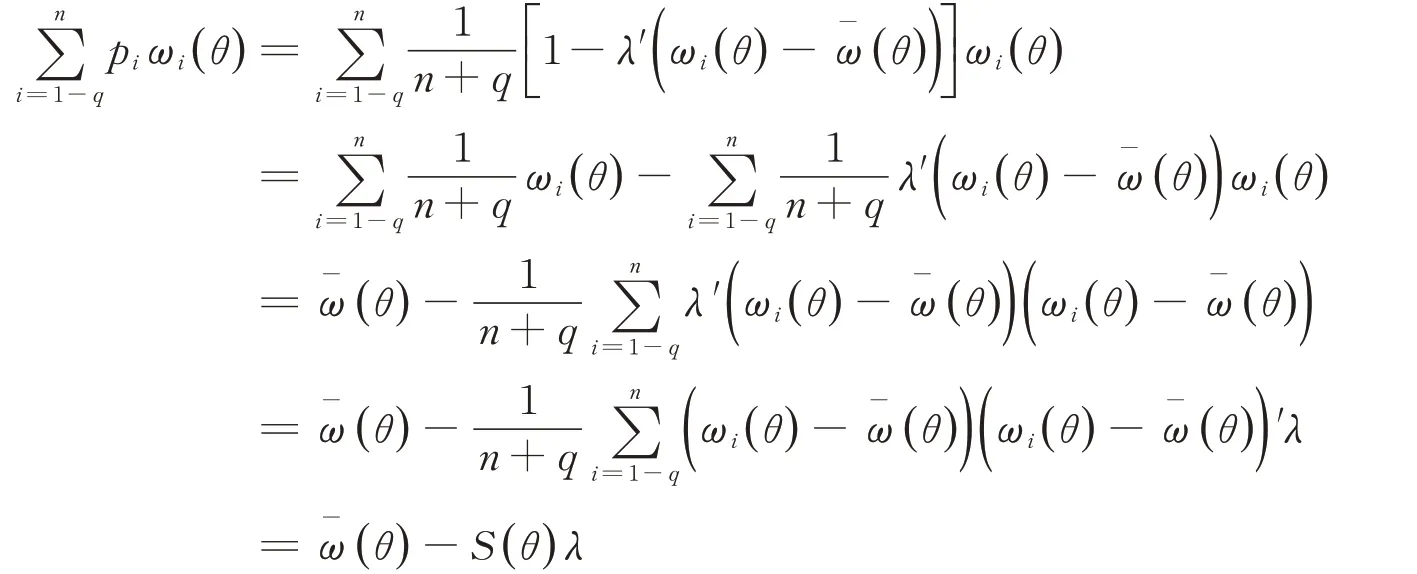
由(8)～(10),得

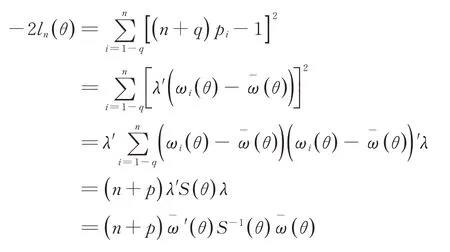
由引理1, 得

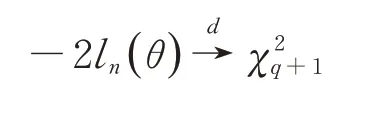
由此完成了定理1 的證明。