小型甘蔗收獲機振動特性的研究與分析
何桂慶,賴 曉,莫瀚寧,2*,曾 邦,曹鉑瀟,滕 筱
(1.廣西大學,機械 工程學院,廣西 南寧 530004 2.梧州學院,機械 與資源工程學院,廣西 梧州 543000)
0 引言
甘蔗是我國重要的經濟作物,而甘蔗產量直接影響著蔗農的收入,由于人工收獲的成本居高不下,甘蔗收獲機的研發與推廣就越來越受到人們的重視。但機械化收獲時,甘蔗的宿根破頭率高是嚴重影響甘蔗收獲機研制和推廣的瓶頸問題之一。現有甘蔗收獲機切割甘蔗時的宿根破頭率高達20%[1]。很多國內外學者對甘蔗收獲機切割系統的動態特性、甘蔗蔸破頭原理進行了研究。美國Valco TD 等[2]進行了高壓水切割甘蔗試驗,結果發現,高壓水切割甘蔗僅限于在室內可行而田間作業時并非理想的切割方式;Mello 等[3]通過高速攝像對比分析了彎角形刀片和光刃刀片的切割效果,結果發現,彎角形刀片比光刃刀片更有利于減少切割損失,提高切割質量;蒙必勝[4]對甘蔗收割機部分結構參數與工作參數影響宿根破頭率破的機理進行了研究,同時提出參數計算公式及優化措施。楊家軍等[5]通過混合模態綜合法建立了小型甘蔗收割機的整體動力學模型,并在該模型的基礎上對其切割器進行動態結構設計。上述研究僅對刀盤和刀片的結構參數、工作參數進行優化,而在動載荷沖擊的情況下甘蔗破損率過高的原理還未從得知,也未曾從動態響應的角度考慮各種激勵載荷的影響規律,其中切割系統與車架連接方式、液壓缸的結構參數的變化等均會影響動態特性和刀盤振幅。
本研究以多體動力學為理論基礎建立整機的動力學模型和虛擬樣機模型,多工況下求解切割器的動態響應,以此分析各激振源對振動的影響規律。
1 建立力學模型
甘蔗收獲機切割系統主要受到路面不平度激振、發動機周期激振和砍蔗力激振等激勵源的影響,但是激振源安裝位置,整機剛度和質量分布對整機動態特性的影響也相當顯著。因此,為了探究激振源安裝位置,整機剛度和質量分布對甘蔗收獲機切割系統振動的影響,將甘蔗收獲機整機簡化為質量—彈簧—阻尼系統[6],四個車輪簡化為彈簧阻尼,如圖1 所示。基于對甘蔗切割質量的敏感性,該動力學模型只考慮垂向振動(沿Z向移動)、橫向扭振(繞Y軸轉動)和縱向扭振(繞X軸轉動)三個方向的自由度,則動力學模型存在車架質心垂向位移X1、繞X軸質心轉角θ1、繞Y軸質心轉角θ2,以及發動機質心垂向位移X2和切割系統垂向位移X3共5 個自由度。
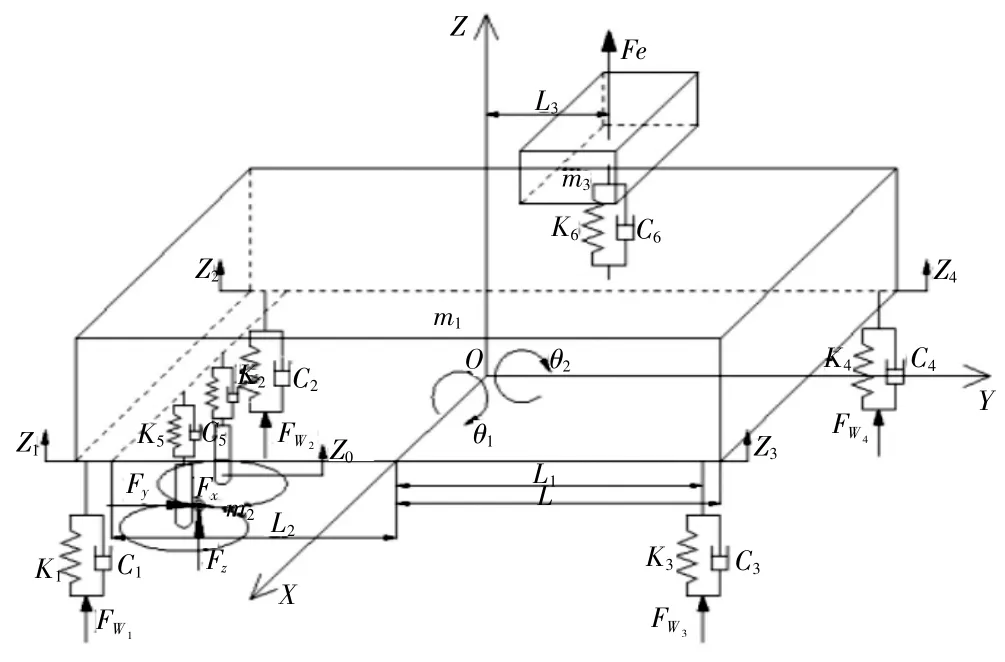
圖1 甘蔗收獲機5 自由度動力學模型
各符號含義,m1、m2、m3分別為:車架質量、切割系統質量、發動機質量;K1、K2、C1、C2分別為:前導向輪的剛度、阻尼;K3、K4、C3、C4分別為:后驅動輪的剛度、阻尼;K5、C5分別為:切割系統和車架之間提升液壓缸的剛度、阻尼;K6、C6分別為:發動機懸置的剛度、阻尼;Fwi為各車輪受到的路面不平度激勵載荷;Fe為發動機垂向激振力;Fx為徑向切割力;Fy為切向切割力;Fz為軸向切割力;L為車架長度距離的一半;L1為前輪或后輪到車架質心的距離;L2為切割系統到車架質心的距離;L3為發動機質心到車架質心的距離;zi為各車輪的垂直向位移;zq為切割系統的垂向位移;θ1為車架繞質心的縱向轉角;θ2為車架繞質心的橫向轉角;垂直向上為正方向,ζ為路面不平度擬合函數,此為簡支梁形式的力學模型,建立以下方程。

Z5為提升液壓缸和車架連接點的鉛錘位移(向上),Z6為發動機的位移(鉛錘向上),Z7為車架位移(鉛錘向上)可得

式中a為1/2 前后輪距,ye為發動機對車架的激振力到車架質心的距離,可得:

將(11)、(12)、(13)、(14)、(15)式矩陣化為MZ¨+CZ˙+KZ=F得整機的數學模型:


式中,M、C、K分別為質量矩陣、阻尼矩陣、剛度矩陣;Z、Z˙、Z¨分別為廣義坐標位移矩陣、廣義速度矩陣、廣義加速度矩陣;F為廣義力矩陣。
通過分析甘蔗收獲機5 自由度動力學簡化模型,發現甘蔗收獲機各部件的質量、安裝位置變化都會對矩陣產生影響,從而影響砍蔗系統的動態響應。由于直接求解砍蔗系統的動力學微分方程組比較困難,而且對于多種激勵作用下砍蔗系統動態響應求解更加困難,因此考慮使用多體動力學軟件進行求解。
2 復雜激勵分析
復雜激振工況下激振源主要包括路面不平度激勵、發動機激振力和砍蔗切削力。課題組前期已經使用五輪儀法采集
廣西丘陵地區甘蔗產地的路譜信號,再通過去均值濾波、積分得到路譜激勵的位移信號,如2 圖所示[9],利用Matlab 工具箱的功能組件cftool 對課題組前期試驗測量的路面不平度時域信號進行最高階為8 階的函數擬合,擬合的結果如圖2 曲線X(t)所示,該擬合函數是由八個正弦函數疊加而成的,其表達式見式(16)。由位移函數可進一步推導出甘蔗收獲機受到路面不平度的激振力,如式(17)所示。甘蔗收獲機樣機的發動機采用四缸直列柴油發動機YCD4J22T-95[10],其往復激振力可由式(18)計算。由前期大量試驗研究結果發現,砍蔗力可由經驗公式(19)計算。
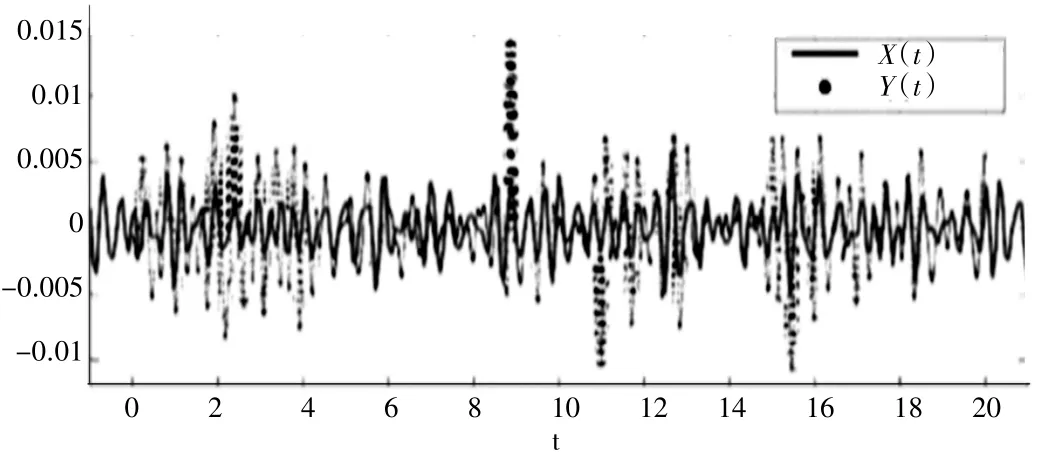
圖2 路面激勵擬合函數曲線
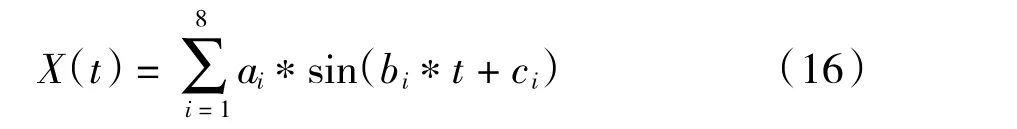
其中ai,bi和ci為擬合常數。

式中,v為刀盤轉速,r為刀盤半徑,θ為刀盤傾角。
3 虛擬樣機仿真
3.1 建立仿真模型
由于刀架垂直方向上的振動對切割質量的影響最為重要,因此仿真試驗只研究路面激勵、發動機激勵和砍蔗激勵共同作用下刀架在豎直方向上的振動特性,并忽略水平方向的振動位移。通過使用Solidworks 三維繪圖軟件設計甘蔗收獲機的模型(圖3)后,保存為Parasolid(*.x_t)格式文件后導入ADAMS 虛擬樣機仿真軟件,如圖3 所示。模型車架部分的質量設置為m1,物流架部分設置為m2,切割系統質量設置為m3,發動機質量為m4。前導向輪和后驅動輪的剛度和阻尼系數采用課題組前期研究的參數,液壓提升油缸和發動機懸置可視為彈簧阻尼連接[9-11],各彈性連接的剛度和阻尼系數(表1)。發動機頻率為50 Hz,且動態幅值±0.1 mm 時,其動剛度系數為1 980 N/mm,粘性阻尼系數為0.15 N/(mm/s)。

表1 彈性連接
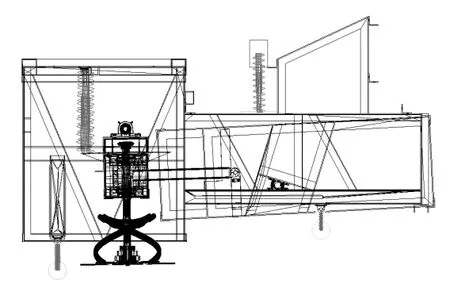
圖3 虛擬樣機模型
為了模擬甘蔗收獲機復雜激勵工況,需要在仿真模型中施加路面不平度激勵,砍蔗力激勵和發動機激勵。在車輪彈性連接處設置運動副和路面不平度激振位移驅動,驅動函數為式(1)所示的的位移擬合函數。在發動機質心處施加周期激振力FORCE_1,并由式(2)-(3)定義激振力函數。在切割刀片的切割點位置分別施加徑向、切向、軸向切割力,考慮到砍蔗時間約為0.075 s,故可采用ADAMS 內置的step 公式定義三向砍蔗力隨時間的變化函數[12]。
3.2 仿真結果分析
只考慮路面激勵作用時,發動機激振力和砍蔗力失效,則切割器振動響應如圖4(a)所示。由圖4(a)可以看出位移響應最大值為1.33 mm,最小值為-3.0 mm,位移的均方根1.356 mm/s,振動速率的均方根值為21.37 mm/s,最大速率為43.96 mm/s。那么在一次砍蔗時間0.0023 s 內刀盤的平均位移和最大位移分別是0.049 mm 和0.101 mm,兩次砍蔗間隔時間0.013 s 內刀盤的平均位移和最大位移分別是0.277 mm 和0.571 mm。只考慮發動機激振力作用時,失效路面激勵和砍蔗力,切割器振動響應如圖4(b)所示,啟動平穩后振動具有周期規律性。刀盤位移響應最大值為0.008 mm,最小值為-0.008 mm,均方根是0.0059 mm。振動速率的均方根為1.83 mm/s,最大速率為2.53 mm/s。那么一次砍蔗時間內刀盤的平均位移和最大位移分別是0.0042 mm 和0.0058 mm,兩次砍蔗間隔時間內刀盤的平均位移和最大位移分別是0.023 mm 和0.032 mm。只考慮三向砍蔗力作用時,失效路面激勵和發動機激振力,切割器振動響應如圖4(c)所示,穩定后具有周期規律性。位移響應最大值為0.235 mm,最小值為0.133 mm,均方根是0.192 mm。振動速率的均方根為5.12 mm/s,最大速率為7.98 mm/s。那么一次砍蔗時間內刀盤的平均位移和最大位移分別是0.011 mm 和0.018 mm,兩次砍蔗間隔時間內刀盤的平均位移和最大位移分別是0.066 mm 和0.103 mm。相比于發動機激勵和砍蔗力激勵,路面激勵為刀盤振幅的主要激勵源。

圖4 切割器振動響應
3.3 復雜激勵
復雜激勵時三種激勵共同作用,切割器振動響應如圖5 所示。由圖5 可知,刀盤位移響應最大值為1.54 mm,最小值為-3.1 mm,均方根是1.501 mm。振動速率的均方根為25.4 mm/s,最大速率為63.6 mm/s。那么一次砍蔗時間內刀盤的平均位移和最大位移分別是0.058 mm 和0.146 mm,兩次砍蔗間隔時間內刀盤的平均位移和最大位移分別是0.33 mm 和0.826mm。
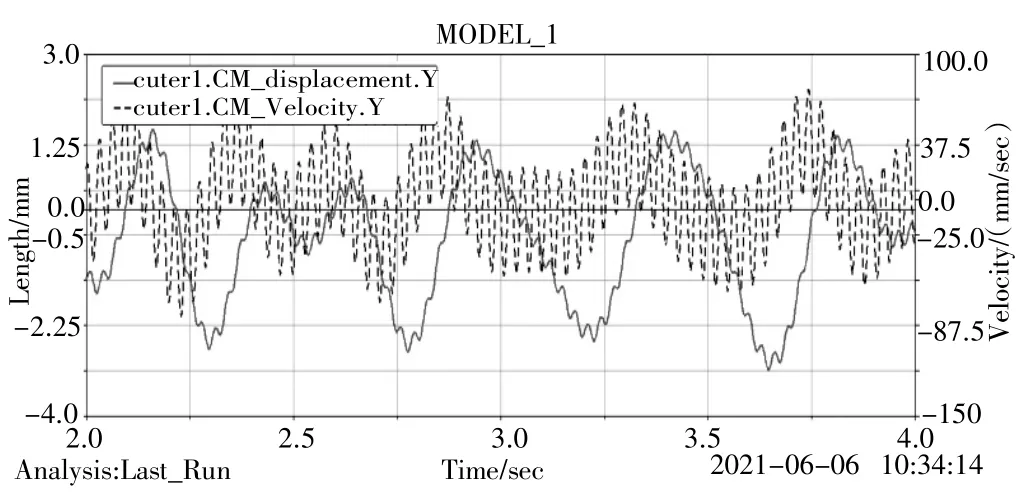
圖5 切割器振動響應
4 結論
本研究建立了甘蔗收獲機5 自由度動力學簡化模型,分析了各部件的質量、安裝位置變化對切割系統振幅的影響。同時建立了虛擬樣機模型研究復雜激勵中的三種激勵源對振動的影響程度,發現路面激勵為主導因素,其次是砍蔗力激勵,最后是發動機激勵,這為后期優化結構設計,降低切割系統的振幅和提高切割質量提供了理論依據。

