基于MATLAB 平臺的雙絞式液壓升降機優化分析
王 軍
(棗莊科技職業學院,山東 棗莊 277500)
0 引言
雙絞式液壓升降機在工程建設中應用十分廣泛,但是對于其結構的優化分析比較缺乏,設計人員往往為省時省力,僅對現成的尺寸加寬、加粗等類比處理,并沒有通過優化系統進行細致的計算和分析。由于傳統方式所制造的升降機,在應用的過程中顯得尤為笨重,己經不能滿足當今快速發展社會的需求,很多方面都需要進行改進;同時,制造廠商不按規范制造升降機,不尊重我國實際情況,照抄國外產品,造成升降機事故頻發。國外研究者C.GANTES 對剪叉式空間結構的非線性特征提出了新的設計理論,并對空間剪叉式機構進行分析驗證。A.S.K.KWAN 基于動力學對剪叉機構的位移運動變化關系進行了探索。在國內武漢理工大學的胥軍對剪叉式升降機的剪叉桿強度進行了校核優化后,提高了舉升機構的穩定性并對升降平臺和油缸的運動過程進行了分析[1];燕山大學王曉楠用剪叉式液壓升降機設計了一種甘蔗收集車,對液壓缸位置進行了參數優化,并運用AMESim 軟件得到升降平臺動力特性曲線[2];大連理工大學的付昱對雙液壓缸剪叉式升降操作平臺進行研究,使用ANSYS 對剪叉式平臺優化分析,運用ADAM 軟件分析了液壓缸動力學特性[3]。但現有研究主要基于靜態力學分析給出的計算方法導入MATLAB 對剪叉液壓升降機進行優化。通過動態力學分析,運用虛功和虛位移方程推導出液壓缸活塞桿的最大推力,對剪叉機構與液壓缸接觸點和上下端點的鉸孔進行力學分析,并基于MATLAB 軟件進行優化,使得在相同推力作用下減少設備的自重和自升高度,減輕了重量節省材料,提升了工作效率。
1 實驗設備
自行走雙鉸接式液壓升降機如圖1 所示。液壓升降機的主要部分包括承重上升平臺、8 個剪叉桿、2 對液壓缸、機架、電機等部分組成。

圖1 自行走雙鉸接式液壓升降機
液壓升降機的參數見表1。

表1 單側車下設備拆裝升降工裝參數
首先對雙鉸接式升降機構進行的參數設定,建立幾何模型。剪叉式升降機的基本構架如圖2 所示,升降機是由兩組液壓缸進行并列鏈接兩組剪叉臂。兩組剪叉臂并列連接在底座上,只需要分析一組剪叉機構的升降運動。
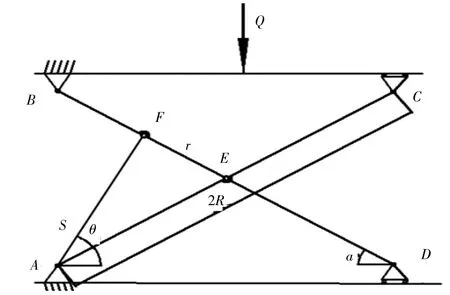
圖2 剪叉機構簡圖
2 升降機構的力學分析
剪叉式液壓升降機的舉升運動主要是依靠驅動裝置液壓缸的推舉實現的。液壓缸活塞桿的最大推力完全影響著剪叉機構的各種性能,在滿足舉升機構舉升條件的基礎上對活塞桿的最大推力進行科學有效的分析能夠改善優化構件[3]。
2.1 靜力學方法分析
靜力學方法就是指通過對物體的受力分析,建立平面匯交力系的平衡方程和平面力偶系方程,對各桿鉸點未知量進行求解。根據雙鉸式剪叉升降機構計一般簡圖幾何關系,液壓缸的軸線S長度為:
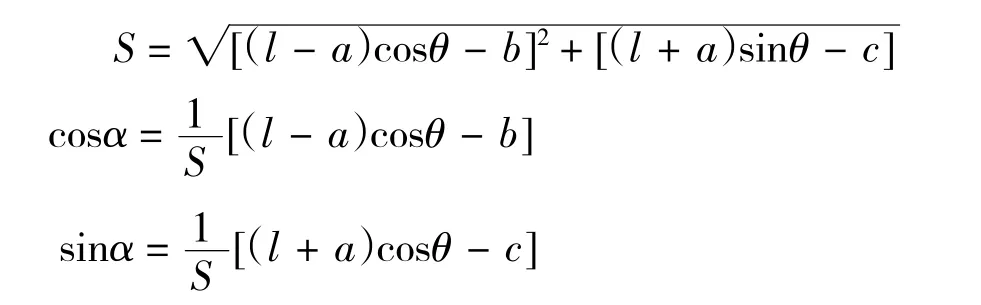
兩個雙鉸點剪叉臂AC、BD的受力分析如3 所示。
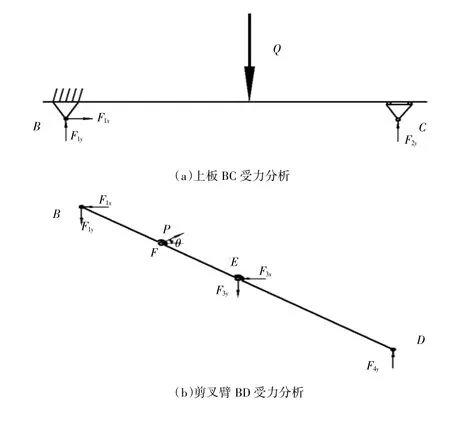
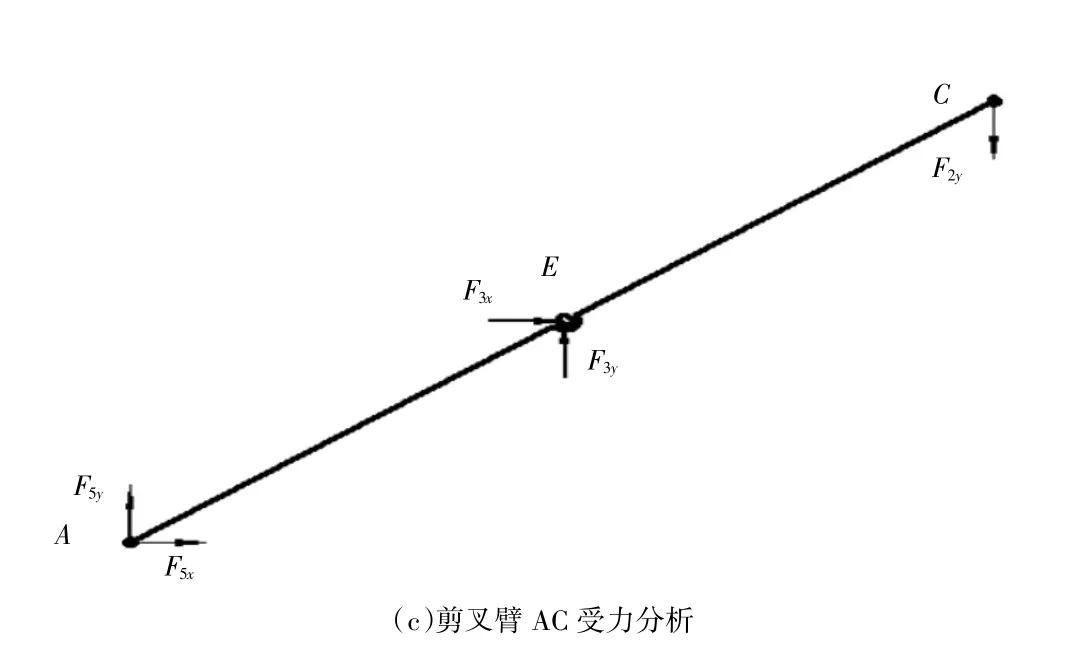
圖3 剪叉臂受力分析
剪叉臂都是對稱布置,因此受力也是對稱的,載荷作用在支點上是受力均分即為G/4。對AC和BD桿進行受力分析,建立平衡系方程:

通過上式推導出液壓缸推力與兩個夾角之間的關系得到液壓缸推力,通過液壓缸推力可以求得各鉸點的受力值:

2.2 虛位移方法分析
通過虛位移和虛功方程對活塞桿的最大推力進行計算求解[4]。
在該數學模型中,雙鉸式剪叉液壓升降機液壓缸的上端與剪叉臂有相對位置關系,而液壓缸下端鉸點與底架連接。圖中剪叉臂長為2R,液壓缸鉸鏈點尺寸為已知數a、b、u、g,液壓缸軸線與水平線的夾角為θ,X為液壓缸活塞桿推出的距離,Y為剪叉式升降機構升降的距離,Q為起升重量,P 液壓缸活塞桿推力,dx為P在x向的虛位移。dy為Q在y向的虛位移。當升降平臺的載重為Q時,液壓缸活塞桿推力P用虛位移原理進行求解
通過圖中幾何關系可以算的:

其中:Q1載重載荷,5 000 kg。Q2升降機自重,3 500 kg。剪叉臂降到最底層與水平面夾角12°。單側剪叉桿的液壓缸最大推力Pmax=5356.5 N。
3 舉升機構優化
液壓缸的伸出末端的鉸接點距離到兩個剪叉臂中間鉸點的距離r參數多少,不僅決定液壓缸安裝距離,也影響到液壓缸最大推力[5]。由于r的取值不同,中間鉸點F的運動軌跡也不同。液壓升降機工作過程中鉸點A固定,鉸點D向右水平滑動,鉸點B、C兩點垂直向上運動。以A為坐標系的原點O建立直角坐標系,其中垂直向上的運動為坐標系的y軸方向,鉸點D運動方向為坐標系的x軸,設中間鉸點F的坐標點為(Fx,Fy):
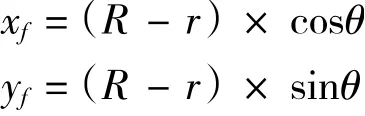
當參數r分別取100、200、300、400、500 時,運用MATLAB 進行編程分析,繪制出中間鉸點F的軌跡圖如圖4 所示,從而為后續約束條件初步確定取值范圍。

圖4 中間鉸點F 軌跡圖
由圖4 可知當參數r=100 mm 時,液壓缸的安裝位置距離最大,液壓缸起升角θ最小,液壓缸伸出軸線最長;當r= 500 mm 時液壓缸的安裝距離最小,液壓缸起升角θ最大,液壓缸伸出軸線最短。由文獻可知,液壓缸起升角θ越大液壓缸所需推力則越小,單一角度看r 越大越好,但是實際中沒有合適的液壓缸。
已知液壓升降機的舉升高度為1.2 m,對模型測量得到有關常量。取值如下:Q=49 000 N;R=1 910 mm;m=2 600 mm;n=720 mm。
運用MATLAB 編程,得到剪叉臂與水平角度θ,液壓缸推力P關于伸出末端的鉸接點距離到兩個剪叉臂中間鉸點的距離r參數三維曲線,如圖5、6 所示。
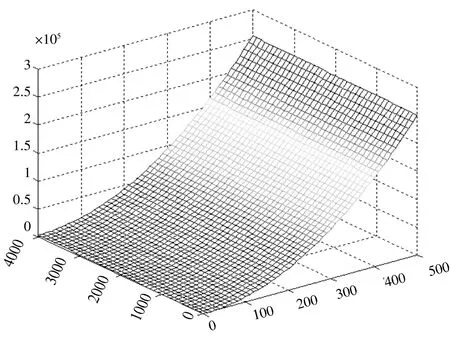
圖5 θ 關于參數a 與h 的變化曲線
由圖5 可知:在活塞桿鉸接位置r一定時,舉升油缸與水平方向的夾角θ隨舉升高度的增加非線性變大;在舉升高度h一定時,θ隨參數r的增加非線性變大,與實際情況相吻合。由圖6 可知:當活塞桿鉸接位置確定時,隨著舉升高度h的增加,舉升油缸推力逐漸減小,并逐漸趨于平緩;當舉升高度h一定時,隨著活塞桿鉸接位置遠離剪叉臂鉸點中(心即參數r增大),舉升油缸的推力隨之非線性減小,并逐漸趨于平穩[6-7]。在保證舉升油缸最大推力盡可能小的前提下,綜合考慮整體布置,做到各部件之間不產生干涉,最終確定a=240 mm。
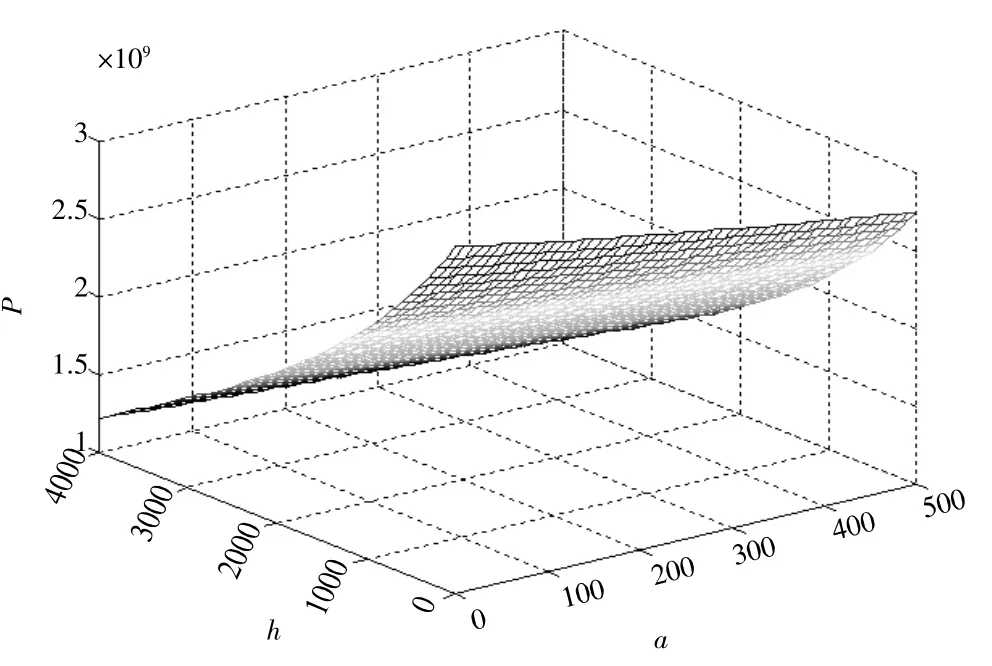
圖6 P 關于參數r 與h 的變化曲線
通過Matlab 的數值分析得到最大推力的最優解,液壓缸的最小推力值Pmin= 44 635 N。在未經過軟件優化時液壓缸在最低位置時,液壓缸最大推力P計算結果為P=53 565 N。通過對比2 種結果可知,經過優化后的液壓缸最大推力減少了16.7%。
4 總結
本文以企業現有的特定型號剪叉式液壓升降機為研究對象,在研究中運用虛位移原理和虛功方程法對液壓剪叉式升降機構的結構分析和承載能力進行計算。通過建立數學模型,使用MATLAB 軟件對剪叉式液壓升降機的油缸進行了受力解析分析,在滿足空間要求的基礎上確定了最小推力時鉸點的位置。通過靜態分析和動態分析結合,使計算更加準確。

