把握真學情 突破重難點 品數學之美
胡錦洪

[摘 要]從課標、教材和學生三個維度去把握學生的真實學情,以真學情促學生真學習,突破重難點,讓學生不僅僅會算,還能真正理解算理,同時品悟數學的智慧之美。
[關鍵詞]多位數乘一位數;學情;算理;算法
[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068(2021)05-0034-02
從兒童已有的認知和經驗出發,準確研判學生的學情,實施精準教學,體驗完整的學習過程,促使學生在獲得知識和技能的同時能知其所以然,品悟數學的魅力。下面以教學人教版教材“多位數乘一位數”第60、61頁內容為例,探討在教學中如何把握學情,突破難點。
一、把握真學情
真學情需要教師透過信息現象看本質,分析把握學生的學習起點,采取有效的教學策略。了解學生學情的方式有很多,筆者就如何讀懂學情、找到真學情,從課標、教材和學生三個方面談一談。
(一)讀懂課標、教材和學生
1.領會課程標準的要求
課程標準指出,在基本技能的教學中,不僅要使學生掌握技能操作的程序和步驟,還要使學生理解程序和步驟的道理。也就是說不僅要使學生會算,還要讓他們知道為什么這樣算。
2.理解教材內容編排意圖
教材中關于三年級“多位數乘一位數”的筆算乘法的內容是這樣安排的:例1教學多位數乘一位數筆算乘法(不進位);例2教學多位數乘一位數筆算乘法(進位),其中例題以兩位數乘一位數(進位)展開,在課本“做一做”中涉及滿幾十進幾和三位數乘一位數(進位)的筆算題目;例3是在例2的基礎上教學連續進位,基本算法和算理與例2是一樣的;例4教學關于0的乘法,說明0和任何數相乘都得0;例5教學因數中間有0的乘法;例6教學因數末尾有0的乘法。通過縱向對比,可以發現教材通過例1引出筆算,幫助學生理解筆算的算理和算法;通過例2、例3突破進位這個難點,其中例2是不連續進位,例3是連續進位,而例3的基本算法和算理與例2是一樣的。
3.深入剖析前測數據信息
課前,教師出示16×3,組織三(1)班41位學生列豎式計算。其中有36位學生計算正確,占全班人數的87.8%。其中用具化豎式的有2位,用簡化豎式的有34位。正確率87.8%,并不代表大部分學生都已經理解并且掌握了兩位數乘一位數(一次進位)的筆算原理,還需要對學生進一步調查。“你能說一說這個進位‘1是怎么來的嗎?這個1為什么要進位到十位上?這個4是怎么來的?為什么不是3?”通過調查,發現只有極少部分學生明白這樣算的道理,大部分學生對具化豎式每一步驟的演算過程和簡化豎式中為什么要寫“4”而不是寫“3”的道理說不清楚,說明大多數學生會算但沒有真正理解算理。
(二)制訂合理的教學目標
1.綜合分析學生學情
綜合課程標準要求、教材編排意圖和前測數據,對學生學情研判得出以下結論:
(1)大部分學生會用簡化豎式正確計算但并不表示學生真正理解這樣算的道理。
(2)具化豎式每一步的算理學生并不清楚,表現出與算理不理解有關。
(3)學生會用簡化豎式計算,雖然能夠寫正確、算正確,但并不清楚算理,也不明白簡化豎式的由來,更多源于直接經驗。因此突破16×3進位“1”,理解算理并會正確計算是本節課教學的重難點。
2.制訂課時學習目標
(1)理解多位數乘一位數的算理,掌握多位數乘一位數的計算方法,并能正確進行筆算。
(2)經歷多位數乘一位數的筆算過程,體驗轉化的思想,提升知識的遷移和類推能力。
(3)感受數學的價值,增進對數學的理解,提高學習數學的興趣。
二、突破重難點
理解簡化豎式每一步的算理和算法,呈現學生的多種算法,溝通算法之間的關聯,并以此突破進位“1”的教學。
(一)創設問題情境,呈現學生的多種算法
教師創設游樂園情境,出示問題:過山車每人玩一次16元,3人一起玩一次過山車需要多少元?學生列式并嘗試探索16×3的算法(如圖1、圖2和圖3)。
(二)表達算理算法,突破學習重難點
在組織反饋圖1、圖2和圖3三種算理算法,內容選擇要先易后難、算理明晰、相互溝通,難點突破要反復體悟。
1.先易后難,依次反饋學習內容
圖1是口算算法,將16拆成10和6,然后分別與3相乘,再相加。該算法對于學生來說并不難,是對該單元“多位數乘一位數”口算乘法內容學習后的再運用。圖2呈現的是具化豎式。理解具化豎式中每一步的算法,就是促進學生理解算理的過程。圖3是簡化豎式。簡化豎式是由具化豎式演變而來的,理解圖2有助于理解圖3的算理和算法。
因此,選擇反饋內容交流的先后順序是圖1→圖2→圖3,這符合學生認知和學習的心理過程,有助于學生的學習。
2.算法溝通,增進彼此算理理解
(1)理解圖2的算理算法
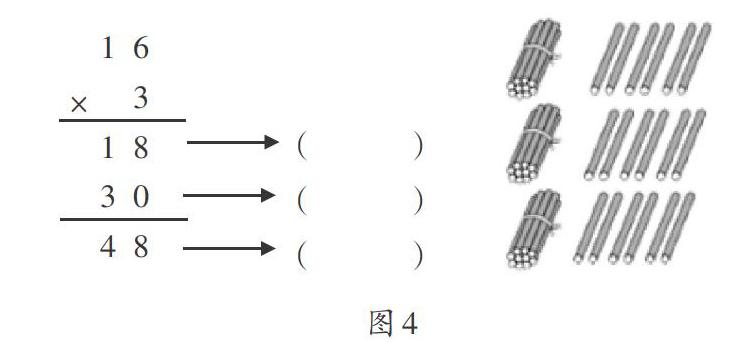
對于圖2,要讓學生明晰具化豎式中18、30和48是怎么來的。學生以任務驅動的形式,自主探究。
①填一填:下列豎式中的18、30、48分別是怎么得到的?請在( )里填算式。
②圈一圈:在小棒圖中分別圈出豎式中的18、30、48。
③說一說:結合小棒圖,說一說16×3的計算過程。
(2)聯系圖1和圖2的算法
學生明晰圖2的算理和算法后,教師要及時組織學生與圖1的口算算法進行聯系,溝通它們的算法關系,增加學生的活動經驗,進一步鞏固具化豎式的計算過程。
(3)理解圖3的算理算法
圖3是簡化豎式,通過前測我們知道,學生會算但不知道這樣算的道理。我們借助圖2,讓學生通過觀察比較,明白簡化豎式簡化了什么?學生發現是18和30合并了,直接寫得數48。教師往往覺得到此可以結束了。如果到此就結束,本節課的重難點還沒有突破。從前測學情來看,圖3恰恰是教學的重難點。筆者在此基礎上,增加了以下教學環節。
①筆者接著問:這個“4”是怎么來的?你能結合剛才的小棒圖圈一圈,說一說嗎?
學生翻開探究單背面的小棒圖,在圈一圈中深刻理解3個十加上進位上來的1個十,得到4個十。
②追問:進位的“1”藏在哪?
學生在簡化豎式中找進位“1”,這個小小的“1”就藏在十位上的右下方。
③回顧:表述算理和算法。
最后,筆者讓學生聯系簡化豎式與小棒圖,說一說計算的過程,既生動又形象。
通過本環節的學習,學生深刻領會簡化豎式每一步的算理和算法,突破進位“1”的學習,理解“4”的由來,增進了對算理的深刻理解。
三、品悟數學之美
(一)體會進位“1”的巧妙之美
學生得出進位“1”寫在十位的右下方。筆者這時候追問:“為什么?”學生說這個“1”表示個位滿十向十位進1。筆者繼續追問:“這個‘1為什么小小的?為什么不可以和其他數字一樣大?是不是地位卑微一些?”學生反駁道:“這個小小的‘1是為了讓我們不要與其他數字混淆,它雖小,但價值卻非常大,是在提醒我們計算的時候不要忘記十位上加上1。”筆者再追問:“那么可以不寫嗎?”學生說:“要寫,這樣不容易忘記,不會算錯。”筆者說:“進位‘1很小,但是它的作用非常大,你想對這個‘1說些什么?”學生說:“你雖然小,但價值超大。”通過交流,學生明白簡化豎式中進位“1”的由來及價值。
(二)體會簡化豎式的簡便之美
對比16×3的簡化豎式與具化豎式哪個更簡便,如果僅僅是從16×3兩個豎式的比較,學生是不能深刻體會簡化豎式的簡便之美的。教師要再出示幾組多位數乘一位數算式,如213×4,2113×4,讓學生再用具化豎式去計算,學生會明顯感覺到簡化豎式的簡便之美。
(三)舉一反三感悟智慧之美
計算16×3的算法是從個位算起,個位滿十向十位進1,那么如果是131×4,2113×4該怎么算呢?以16×3算理和算法為學習起點,通過類比、遷移讓學生明白無論乘得哪一位,只要滿十就向前一位進1。通過算法的遷移,學生進一步理解算理,貫通多位數乘一位數單元內容的學習,感受到數學學習之美。
總之,精準把握學生的學情,透過現象看本質,深究教學內容和教學方式,能促使學生在情感態度價值觀等方面得到發展,為學生的未來學習奠定基礎,發展學生的數學核心素養。
(責編 吳美玲)

