湖泥—水泥膏漿的堆積擴散特性試驗研究

于佳維 ，彭國威 ，張可能 ，張云毅 ，王穎卓

（1.江西銅業股份有限公司 城門山銅礦，江西九江 332000 ；（2.有色金屬成礦預測與地質環境監測教育部重點實驗室，湖南長沙 410083;（3.中南大學 地球科學與信息物理學院，湖南長沙 410083）

膏狀漿液是指抗剪屈服強度大于20 Pa、塑性黏度也大的混合漿液。該類漿液性狀類似牙膏，流動性小，適用于大孔隙地層(如巖溶空洞、巖體寬大裂隙、堆石體等)中的灌漿[1]。湖泥—水泥膏漿屬于黏土漿液系漿材，以湖泥為主要原料配制一定濃度的湖泥基漿后加入水泥、膨潤土、水玻璃等，其黏度大、無自流動性，且堆積體具有自穩性[2-4]。大多學者在研究膏狀漿液時，主要是針對其物理力學性能以及抗沖釋性、可泵性等進行室內試驗[5-7]，探索更佳的漿液配比，而對膏狀漿液堆積特性研究較少。

而在礦山采空區的處理中，常常采用與膏漿有相似性能的膏體進行充填，其中吳愛祥團隊[8-11]分析了泵送劑對膏體流動影響，探討了漿料對管道輸送阻力特性，對膏體在管道中的流動特性進行了研究；朱世彬等[12]研究了高濃度漿液在采空區中的堆積擴散規律以及漿液堆積體角度對充填墩柱承載力的影響；白仲榮等[13]對膏體充填料漿在空洞型采空區中的流動堆積特性進行了探討；湯麗等[14]研究了無限水平面上充進行了填料漿堆積的數學模型。本文通過室內模擬注漿試驗，觀測湖泥—水泥膏漿的流動擴散特性，發現膏漿的堆積體與膏體有相似之處，結合前期對湖泥—水泥膏漿性能研究、膏體堆積特性，以及室內模擬注漿試驗探索湖泥—水泥膏漿的堆積擴散特性，擬建立漿液堆積體各參數與注漿量和漿液坍落度的理論數學模型。

1 室內模擬注漿試驗

1.1 模擬注漿試驗裝置

模擬注漿試驗裝置主要包括注漿系統和注漿腔體。注漿系統由軟管泵、注漿軟管、壓力表以及電磁流量計組成（圖1），可模擬現場漿液泵送情況。軟管泵最大轉速為50 r/min，最大泵送量為50 L/h；注漿管內徑為50 mm。壓力表可監測注漿過程中注漿壓力的變化；電磁流量計可記錄注入注漿腔體中漿液的體積。注漿腔體為帶有有機玻璃的磚砌腔體，通過有機玻璃可觀察漿液擴散情況，具體尺寸為200 cm×150 cm×70 cm。

圖1 試驗裝置實物

1.2 試驗漿液配比

根據前期測試湖泥—水泥膏漿所得的物理力學性能，以坍落度作為衡量漿液黏稠程度的主要指標，選取幾組典型不同坍落度的漿液配比進行模擬注漿試驗，控制試驗變量為漿液坍落度和注漿量，具體漿液配比如表1 所示。

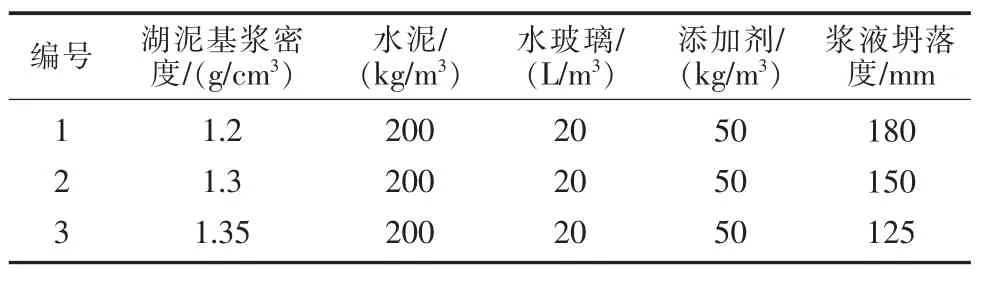
表1 不同坍落度的漿液配比

1.3 試驗方法

本試驗旨在探索不同湖泥—水泥膏漿在無限制水平面上的擴散規律，主要包括漿液配制、泵送試驗以及測量漿液堆積體尺寸三個部分。先按照一定漿液配比配制湖泥—水泥膏漿，為減少漿液黏度的時變性帶來的誤差，漿液配制后立即進行泵送試驗；泵送試驗完成后，測量漿液堆積體的高度、寬度等參數。

2 湖泥—水泥膏漿的堆積擴散

通過不同漿液配比配制不同黏度的漿液，測試好坍落度后進行泵送試驗。觀測漿液的流動規律及堆積體的參數。從出漿管排出的湖泥—水泥膏漿注入平面無限制空腔內堆積成錐狀堆體，頂部為一個圓形沖坑，注入坑內的漿液不斷向沖坑向周邊溢出，并沿堆積體均勻。不同坍落度漿液形成的堆積體見圖2。

圖2 不同坍落度漿液形成的堆積體

如圖2 所示，為不同坍落度漿液（不同黏度）形成不同形狀的堆積體，可見堆積體曲線可類比于正態分布函數曲線。當漿液黏度較大即坍落度較小時，堆積體表現出正態分布函數里的均方差較小，圖形表現為“又高又瘦”；當漿液黏度較小即坍落度較大時，堆積體表現出正態分布函數里的均方差較大，圖形表現為“又矮又胖”，其幾何參數見表2，近似圓臺的立體模型如圖3 所示。

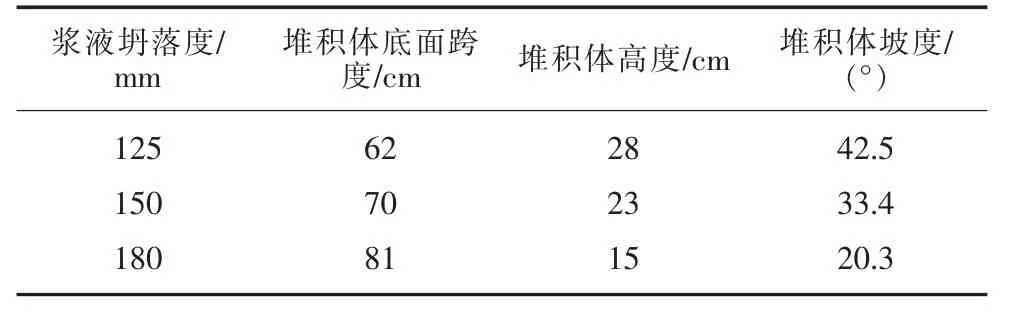
表2 不同坍落度的堆積體參數

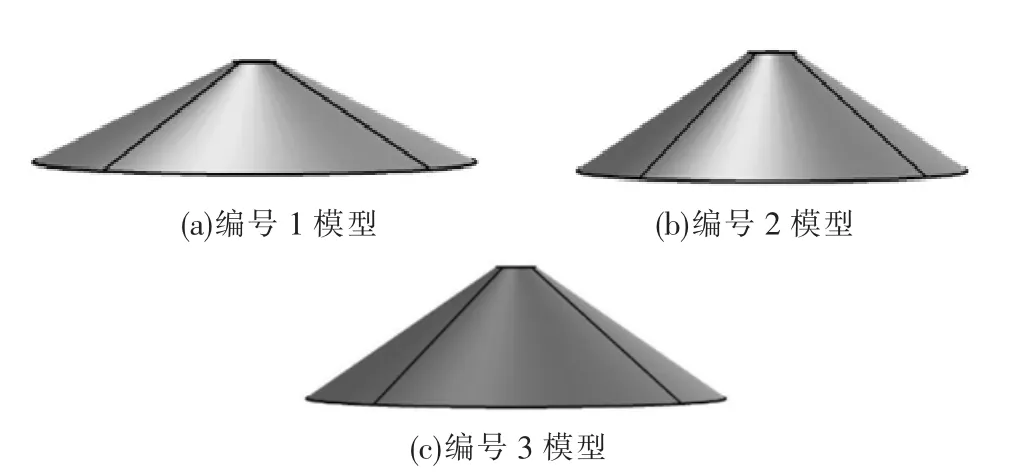
圖3 不同坍落度漿液堆積體模型

3 堆積體參數分析

為了更加準確地研究漿液堆積體各參數之間的關系，以堆積體寬度方向（水平方向）為X 軸，以堆積體高度方向（豎直方向）為Y 軸建立X-Y 坐標系，如圖4 所示，將堆積體剖面放入X-Y 坐標系中。

為了探索堆積體各參數之間的數學關系，引用正態分布的密度函數，其中在研究的堆積體模型中可認為所有圖形皆關于 y 軸對稱，所以 μ 為 0。σ 為正態分布的均方差，σ 越大，數據分布越遠，圖形表現為“又矮又胖”；σ 越小，數據分布越集中，圖形表現為“又高又瘦”。

對于堆積體的數學模型，均方差的大小反映了流動后形成表面的平緩或陡峭，在實際注漿過程中決定著注漿段長、 注漿管移動次數以及注漿孔之間的間距等，因此非常重要。不考慮被水帶走的漿液，其值主要與漿液的黏度有關，即和漿液的配比有直接關系。為了更好地指導現場施工，應探索坍落度與均方差之間的經驗公式。隨著漿液不斷注入無限制的空腔中，漿液堆積體體積不斷增大，堆積體也會越來越高，四周擴散越來越遠，但是整體還是會呈正態函數曲線的“鐘型圖”，如圖5 所示。所以，堆積體的形態除了和漿液坍落度有關外，還和注入的漿液量以及注漿時間有關。

不同黏度漿液形成的堆積體曲面陡峭不一，黏度較大的漿液堆積體對應均方差較小的鐘型圖，黏度較小的漿液堆積體對應均方差較大的鐘型圖。隨著漿液不斷注入，堆積體不斷增大，保持和原有相似的坡面曲線，近似于在原有的基礎上擴大了倍數。幾種典型的正態分布函數見圖6。

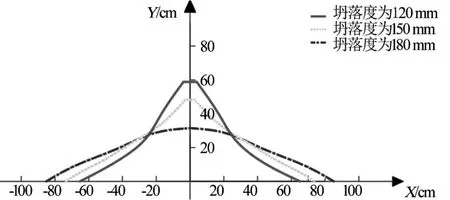
圖5 堆積體規模不斷增大剖面示意

圖6 幾種典型的正態分布函數

根據模擬注漿實驗以及漿液性能試驗可知，大部分湖泥—水泥膏漿堆積體剖面曲線對應的正態分布函數方差應處于1.0～5.0 之間，不會出現像圖6 中σ2為0.5 的情況。根據實驗結果近似推出不同坍落度對應的正態分布方差如表3 所示。

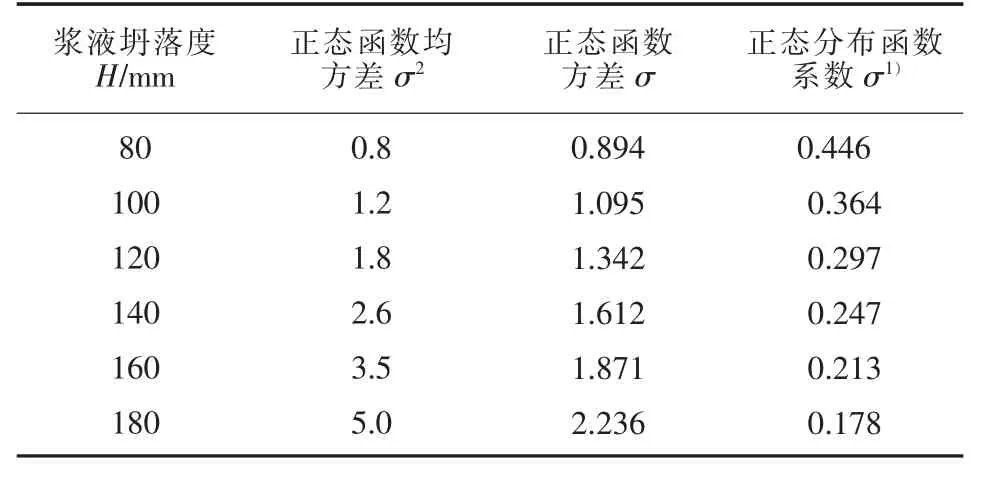
表3 不同坍落度對應正態分布函數方差經驗

為了得到系數β，采用反算注漿量的方法。因為注漿量可通過流量計讀出，所以可認為Q 已知。Q的計算公式見式（1）：

在式（1）中，對于某一特定漿液來說，坍落度可知從而可得α 和σ2。解此定積分可得系數β 關于注漿量 Q 的關系式，見式（2）：

綜上所述，可得單個湖泥—水泥膏漿堆積體各參數之間的函數關系為：

式中：f（x）為漿液堆積體的高度；Q 為漿液注入量；σ2為不同漿液坍落度對應的正態分布函數方差，可查表3。

通過推導的公式可知，在泵送湖泥—水泥膏漿時通過測試漿液的坍落度以及記錄漿液注入量，可以預測漿液的流動范圍以及漿液堆積體的位置與規模，為確定注漿孔距、注漿段長提供參考。

4 結論

1）湖泥—水泥膏漿進入無限制的溶洞內后，克服自身的黏聚力和底面阻力后，慢慢堆積起來形成一個近似圓臺形的堆積體，堆積規律近似正態分布，其坡面曲線近似正態分布函數，均方差（σ）決定坡面曲線的平緩程度，σ 的大小主要取決于漿液的坍落度，并且隨著漿液不斷注入，堆積體規模隨之增大所以堆積體的曲線函數還和注漿量有關。

2）在以往的工程實踐中，對于溶洞充填確定鉆孔間距主要是根據施工經驗，存在一定的盲目性。掌握漿液的流動規律后對于提高充填質量、 確定鉆孔間距等有一定的指導作用。