放縮法證明數列不等式的策略探究

甘肅省蘭州市第六中學(730060) 焦永垚

數列不等式的證明是高中數學中的重點和難點,是歷年高中各類考試中的熱門考點,這類問題通常難度較大,具有很高的綜合性與靈活性.本文以2019年全國高中數學聯賽貴州省預賽試題(B)卷第16 題為例,從不同角度探尋放縮法證明數列不等式的策略與方法,重點闡述如何選擇合理地放縮思路,如何準確把握放縮的“尺度”,以期能幫助同學們從根本上認識放縮法的規律,從而優化解題方法,提升解題能力,提高解題效率.

一、試題分析

題目設數列{an}的前n項和Sn滿足:Sn=k·qn?k,其中k,q為非零常數,且a1=3,a4=81.

(1)求數列{an}的通項公式;

(2)設bn=an ?證明:

分析第(1)問考查數列的基礎知識,易求得an= 3n.第(2)問是數列不等式的證明,數學歸納法是解決這類問題的優選方案.

當n=1 時,不等式成立.

假設當n=k(k ∈N?) 時結論成立, 即那么當n=k+1 時, 因為bn ?3bn?1=＞0, 所以bn ＞3bn?1, 即(n≥2), 則即當n=k+1 時不等式也成立.

綜上,對于一切正整數n,不等式都成立.

可以看到,上述方法中我們需要克服以下三個難點:

(1)如何利用歸納假設?

要證明當n=k+1 時結論也成立,如何利用歸納假設,是解決問題的的關鍵, 為了利用假設, 我們需要找出與的關系, 要找出的等量關系難度太大,所以考慮它們的不等關系,也就是放縮.

(2)怎樣放縮?

因為bn= 3n ?容易發現{bn}為遞增數列,所以(n≥2), 因此我們會首先做這樣的嘗試: 當n=k+ 1 時,放縮過度了.

(3)如何調整放縮度?

經歷(2)的嘗試,發現放縮過度了,需要調整放縮的度:如果忽略bn= 3n ?中的則有bn= 3bn?1(n≥2),于是我們猜想bn ＞3bn?1,是否成立呢? 因為bn ?3bn?1=＞0,所以bn ＞3bn?1,可得(n≥2),再進行計算發現剛剛好.

從以上過程可以看到,放縮法是證明數列不等式的重點和難點,因此我們有必要進一步探究放縮法證明數列不等式的思路與策略.

二、思路探究

思路1放縮成一個等比數列

策略1利用不等式放縮,其中a ＞b ＞0.因為于是,當n=1 時,不等式成立;當n≥2 時,

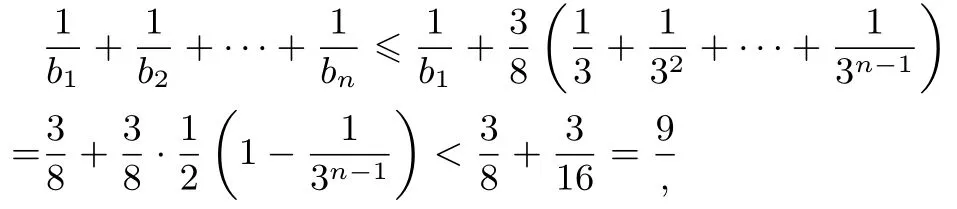
綜上,對于一切n ∈N?,都有

點評在證明數列不等式的問題中, 對于形如(a ＞b ＞0) 的數列,通常可以利用不等式將其放縮為一個等比數列.

策略2利用不等式3n≥2·3n?1+ 1 放縮.因為3n ?2·3n?1= 3n?1≥1, 所以, 對任意n ∈N?, 都有3n≥2·3n?1+1 成立.所以,于是, 當n= 1 時,當n= 3 時,當n≥4 時,

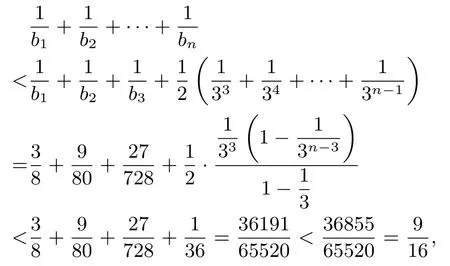
綜上,對于一切n ∈N?,都有

點評此證法中如果只保留第一項,從第二項開始放大,則放縮過度了;如果保留前兩項,從第三項放大,則＜依然太大了,只有保留前三項,從第四項開始放大,才能得到符合的結果.因此,當出現放縮過度的情況時,就要適時進行“局部調整”,保持前若干項不變,從后面的項開始放縮,反復嘗試,直至成功.

思路2向裂項相消放縮

宮頸成熟能夠提高順利分娩的幾率,近來常用的促進宮頸成熟的方法有乳房按摩方法[6]。本篇文章設置對比實驗,對照組使用常規孕產婦檢查方法,實驗組在常規方法基礎上使用乳房按摩方法。實驗結果說明實驗組孕產婦的宮頸評分以及總有效率,遠遠高于對照組,說明乳房按摩能夠促進宮頸成熟。

策略1放縮成的形式,λ為常數.當n≥2 時,

所以,當n= 1 時,; 當n= 2 時,當n≥3 時,

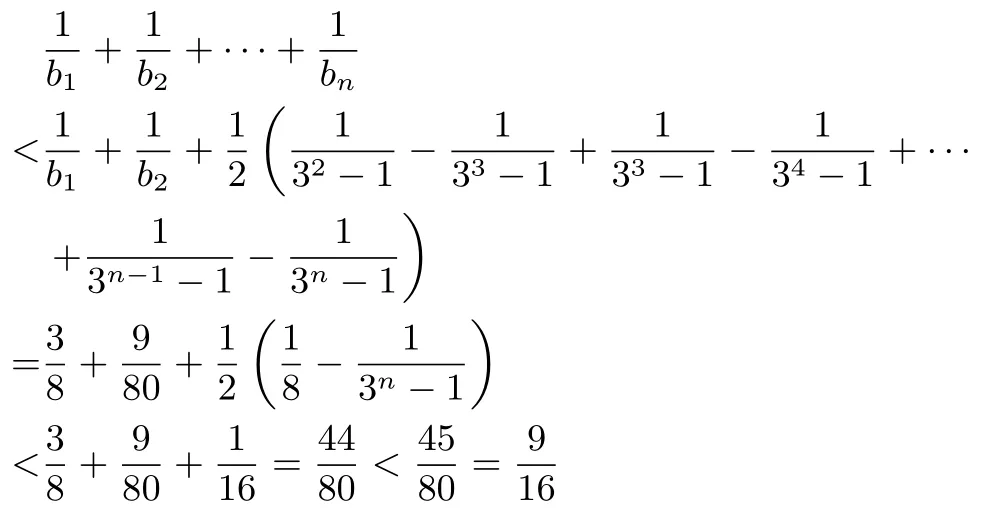
綜上,對于一切正整數n,都有

策略2放縮成

的形式,λ為常數.因為為了便于用裂項相消法求和, 所以我們聯想能否把中的全部或者部分項放大成的形式.我們先逆向進行探索, 因為所以要使, 只需只需只需3n+3＜2·3n ?2, 即3n ＞5, 顯然當n≥2 時成立, 所以, 當n≥2 時, 有于是當n= 1 時,當n= 2 時,當n= 3 時,當n≥4 時,

綜上,對于一切正整數n,都有

思路3利用“糖水不等式”放縮

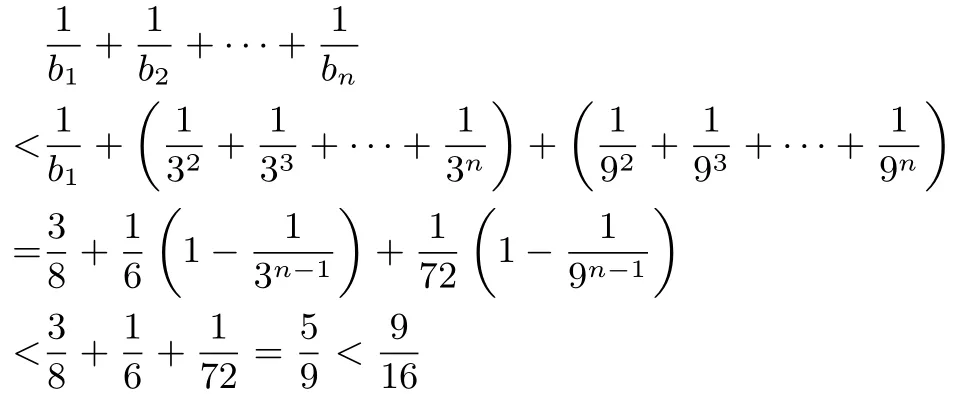
綜上,對于一切正整數n,都有

思路4利用分項比較法放縮

策略1執果索因, 逆推探源.不等式的左邊是數列的前n項和, 右邊為一個常數, 結合的結構, 我們聯想, 把右邊常數縮小成某個等比數列{cn}的前n項和, 然后只需證明≤ck就可以了, 其中k= 1,2,···n.那么{cn}究竟等于什么呢? 我們可以逆推回去: 要證成立, 只需證成立, 設數列{cn}的前n項和Tn=則當n≥ 2 時,cn=Tn ?Tn?1=,當n=1 時,c1=T1=符合上式,故cn=.于是,由≤0 可得≤ck, 其中k= 1,2,···n, 所以即

策略2逆用累加法.同思路4, 先把常數縮小為即要證,只需證

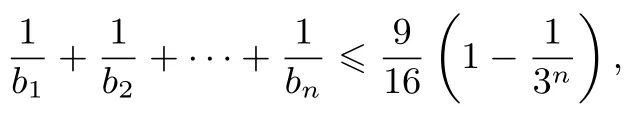
而

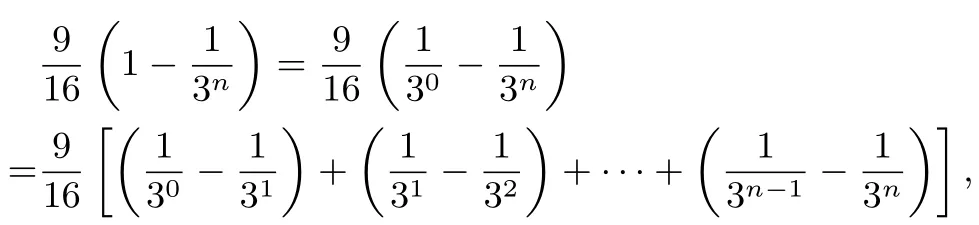
三、小結反思

數學歸納法和放縮法都是證明數列不等式的常用方法,而放縮法通常學生感覺無從下手,不知所措,主要表現在以下幾個方面:

(1)用什么方法放縮? 首先要搞清楚到底是放大還是縮小,再考慮采用哪種放縮方法.常見的方法有利用均值不等式、“糖水”不等式、放大(或縮小)分子(或分母)、一些常用的不等式等等.

(2)向什么方向放縮? 對于像母題中與數列前n項和有關的不等式,放縮的原則是經過放縮后能夠求和,比如放縮成一個等比數列、向裂項相消放縮等等.

(3)如何把握放縮的度? 我們經常會遇到放得“太大”或“太小”的問題,這就要求調整放縮的尺度,例如在本文中,當我們發現放縮得“太大”時,就要采取補救措施,即保留前若干項不變,對后面的項進行放縮,逐一嘗試,直至成功.

另外,本文中的這道競賽題是一道典型而設置巧妙的考題,它之所以能引起我們強烈的共鳴與反響,不僅僅是因為其獨特的解題思路與技巧,更是因為問題中所蘊含的豐富的數學知識思維和思想方法.這樣的題目有利于學生模式化解題的總結,不僅僅教會了學生怎樣解題,而且還有效地培養了學生思維的廣闊性和靈活性,提高了解題效率.