W(2)到Kac模的權導子空間

劉舒暢,王淑娟

(黑龍江大學數學科學學院,黑龍江 哈爾濱 150080)

1 引言

本文約定基域F的特征p>2.令域F上向量空間V,連同它的值和分解V=Vˉ0⊕Vˉ1稱為一個Z2-階化空間.若v∈Vθ,其中θ∈Z2,則稱v為Z2-齊次元素,用|v|表示Z2-齊次元素的次數.為方便,如果符號|v|出現,那么約定v是Z2-齊次元素.若V的一組基為v1,...,vn,則可記為V:=hv1,...,vni.用hg(V)表示Z2-階化空間V的所有Z2-齊次元素的集合.設L是李超代數,M為L-模.稱Z2-齊次線性映射?:L?→M為次數為|?|的齊次導子,如果

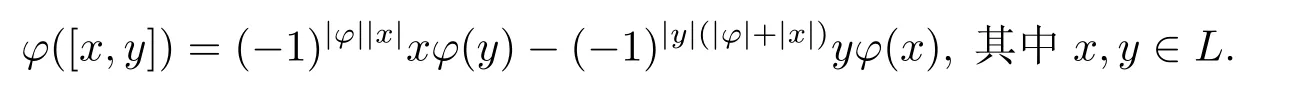
令Der(L,M)為L到M的所有Z2-齊次導子張成的向量空間,稱該空間中的元素為導子.對于Z2-齊次元素m∈M,令

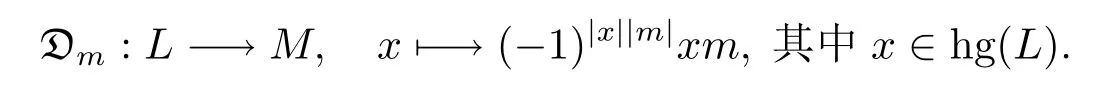
那么Dm是次數為|m|的Z2-齊次導子.令Ider(L,M)為由{Dm|m∈hg(M)}張成的向量空間,稱該空間中的元素為內導子.令h為Lˉ0的Cartan子代數.設L與M都有關于h的權空間分解:L=⊕γ∈h?Lγ,M=⊕γ∈h?Mγ.令

稱HomF(L,M)(0)與Der(L,M)(0)中元素分別為關于h的權映射與權導子.那么

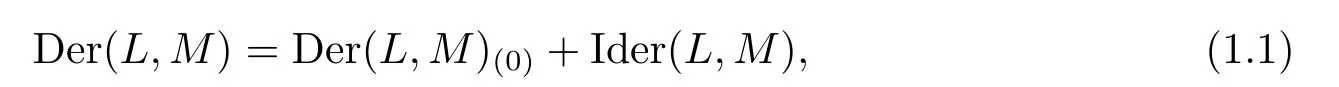
這個結論可參見文獻[1,Lemma 3.2]或[2,Lemma 2.1].值得注意的是,L到M的一階上同調

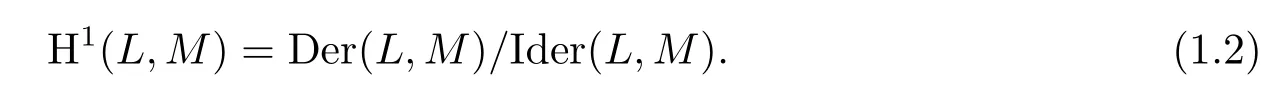
(1.1)與(1.2)得到,計算一階上同調可以先計算權導子空間.本文目的在于決定Witt型模李超代數W(2)到其Kac模K(λ)的權導子空間,取得下面主要結論,其對刻畫W(2)的一階上同調具有重要意義.

定理1當λ=0時,W(2)到Kac模K(λ)的權導子空間是一維的,否則權導子空間是零維的.

本文研究的W(2)屬于Cartan型模李超代數的范疇,具體地說,W(2)是一類Witt型模李超代數.1986年,沈光宇老師對這類代數的階化模做了研究[4];2007年,劉文德老師和張永正老師對其導子代數做了研究[5];2010年,舒斌老師和張朝文老師對其限制表示做了研究,并且定義了Kac模[6].李超代數的上同調是重要的研究課題,其定義可追溯到D.A.Leites在1975年發表的文章[7].2014年,孫麗萍老師、劉文德老師和吳勃英老師利用權空間分解的方法,刻畫了在特征大于2的代數閉域上,sl(m,n)到Cartan型李超代數W和S的低階上同調,并且指出這一計算結果與特征零的情形不同[8].

2 預備知識

利用(2.1)?(2.3)及引理2.1,可以得到Kac模K(λ)的模作用表.

表1 模作用表

3 權導子空間

本節主要是分步驟證明定理1.

解得:

經過上述計算,上述所有情況中,滿足導子定義的每個方程組都只有零解,結論得證.

由引理3.1,3.3以及3.5易得定理1.