塑性流動擠出切削制備梯度結構鋁薄板的仿真分析*

鄒銀輝 鄧文君

(華南理工大學機械與汽車工程學院，廣東 廣州 510640)

大塑性變形(severe plastic deformation,SPD)工藝作為提高材料性能的可行方法之一，得到了廣泛的關注。迄今為止，相關研究人員已經提出了許多SPD工藝，例如等通道轉角擠壓(equal channel angular pressing,ECAP)[1-2]、高壓扭轉(high pressuretorsion,HPT)[3-4]、累積疊軋(accumulative roll bonding,ARB)[5-6]、扭轉擠壓(twist extrusion,TE)[7-8]與大應變擠出切削(large strain extrusion machining,LSEM)[9-11]等。SPD工藝最為顯著的優勢是能夠在室溫下將材料的初始粗大晶粒轉化為超細晶粒，從而使其機械強度明顯提高[12-13]。但是，目前絕大多數SPD工藝在使材料得到較高機械強度的同時，延展性不可避免地出現顯著降低，這很大程度上限制了SPD工藝在工業上的應用[14-16]。因此，尋找一種可以兼顧材料高強度與高塑性的新型工藝尤為重要。

Vu V Q等[17]提出了一種新型的SPD工藝-塑性流動擠出切削(plastic flow machining,PFM)工藝，通過可控的側向擠出切削過程將大塊工件的表層分離出來，并將其轉化為具有超細晶粒與梯度結構的薄板[18]。所制備的梯度結構鋁薄板沿厚度方向呈現明顯應變梯度，且晶粒尺寸由一側的超細晶粒逐漸過渡到另一側的粗大晶粒[19-20]，其強度明顯增大，延展性也得到了極大提高。Vu V Q等[21]通過實驗表明，PFM工藝制備的商用純鋁Al1050薄板的抗拉強度提高到原材料的3倍，均勻延展性約6%，且其各向異性系數為0.92，大于傳統軋制(0.5～0.85)，而較高的各向異性系數對提高鋁板的成形性具有重要意義。但是，該實驗均在同一模具中進行，沒有改變其結構參數，即缺少模具結構對梯度結構薄板成形影響的相關研究。這在研究上是有所不足的，因為就該工藝而言，模具結構對梯度結構薄板成形起到了關鍵甚至決定性的作用，研究其對薄板成形的影響十分必要。

本文采用DEFORM軟件，對不同模具結構下梯度結構鋁薄板的成形進行了模擬仿真，研究分析了其對梯度結構鋁薄板側向擠壓比及等效應變的影響，為梯度結構鋁薄板的制備提供借鑒。

1 PFM工藝的原理

PFM工藝原理如圖1所示，初始工件高度為H，寬度為D(垂直紙面方向)，模擬中統一取為20 mm，即工件橫截面為一正方形。通過壓力P將工件以恒定速度壓入水平方槽模具中，經擠壓后其高度縮減為H1，模擬中統一取為17.5 mm，故擠壓厚度H2=H-H1=2.5 mm。模具側面有一個長方形開口，模擬中統一取開口寬度h為1 mm，開口長度l(垂直紙面方向)等于初始工件寬度D，即l=D=20 mm。Hill R[17]研究表明，當厚度比r=H2/H的取值在0.01～0.15時，高壓區域附近被塑化的材料很容易流入細縫之中，而本研究中r恒等于0.125，滿足上述條件，故模擬過程中材料也可從側向開口擠出。采用恒定壓力Pb作為背向壓力，以控制材料流動。開口左側與橫向通道之間存在圓角，即開口圓角R。開口右側與橫向通道之間存在拐角，即擠壓角度C。由于R和C均與梯度結構薄板成形密切相關，且它們都比較容易控制，故選用這兩個參數作為變量對不同梯度結構鋁薄板的成形進行研究。

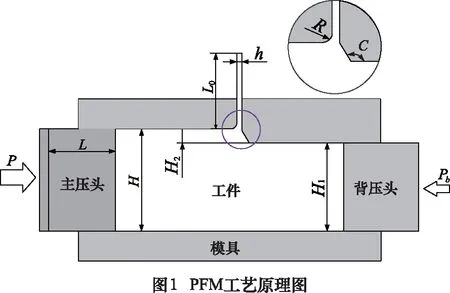
作為一種金屬成型工藝，PFM工藝與傳統的切削加工工藝存在許多相似之處，但有著本質的區別。在PFM工藝中，材料分離基于高壓應力下材料的塑性流動。而傳統切削加工中，材料分離直接由刀具產生，所涉及應力為拉應力。因此，兩者的成形原理完全不同。

2 有限元模擬

2.1 模型設置與材料建模

由于模具中側向開口的長度l遠大于寬度h，滿足平面應變條件，故本文將原始模型轉換為較為簡單的平面應變模型，采用基于拉格朗日公式的大塑性變形分析軟件DEFORM-2D進行模擬。

將工件材料定義為ALUMINUM-1050A，采用基于Hollomon函數[22]的馮米塞斯模型：

(1)

式中：σ為等效應力，MPa；ε為等效應變；n為應變指數；m為應變率指數；c與y均為與材料相關的常數。利用Arzaghi M等[23]研究所得Al1050的應力-應變曲線確定了相關參數，如表1所示。

表1 Al1050的馮米塞斯模型相關參數

表1 Al1050的馮米塞斯模型相關參數

符號nmcy取值0.2301800

2.2 熱物理特性與摩擦模型

在室溫下，SPD工藝過程中溫度升高很不明顯。對于鋁材而言，其溫升一般不會超過5 ℃，例如Zhilyaev A P等[24]采用變形最為劇烈的SPD工藝-HPT制備鋁材，其溫升也只有接近5 ℃，這主要由于材料變形緩慢所造成。本研究中主壓頭速度恒為1 mm/s，材料變形緩慢，溫升不大，對薄板成形影響很小，故可忽略其熱物理特性。

2.3 評價指標

為了描述梯度結構鋁薄板的成形效果，本文引入側向擠壓比x、左側等效應變εL及右側等效應變εR作為評價指標，其中側向擠壓比x是指薄板成形體積V0與工件擠入體積V的比值。

如圖1所示，由于模擬步數為1 600步，步長深度為0.025 mm，故工件擠入長度L=1 600×0.025 mm=40 mm。對于所制備的梯度結構鋁薄板，其厚度(沿壓力P方向)基本等于開口寬度h，可用h代替，寬度(垂直紙面方向)基本等于開口長度l，可用l代替，并將側向擠出距離定義為薄板長度L0(沿擠出方向)。因此，所求側向擠壓比

(2)

式中：x為側向擠壓比；L0為梯度結構鋁薄板長度，mm。

此外，將所制備的梯度結構鋁薄板的左側等效應變εL及右側等效應變εR作為另兩個評價指標，以更好地描述其成形效果。

3 模擬結果與討論

為了更好地解釋擠出切削過程中金屬的塑性流動，本文對PFM模型材料塑性流動的區域進行了劃分，并將經側向開口擠出的材料與經橫向通道流出材料之間的邊界定義為材料分流邊界，即材料分流邊界以上的材料基本經開口擠出，而材料分流邊界以下的材料基本經橫向通道流出。如圖3所示，當材料橫向流動阻力較小或開口擠出阻力較大時，材料分流邊界位于區域1，材料很難經開口擠出，故從開口擠出的材料相對較少；當材料橫向流動阻力增大或開口擠出阻力減小時，材料分流邊界位于區域2，故從開口擠出的材料有所提高；當材料橫向流動阻力很大或開口擠出阻力很小時，材料分流邊界位于區域3，大部分材料經開口擠出，故從開口擠出的材料接近峰值。

3.1 開口圓角對鋁薄板成形影響分析

為了分析開口圓角對梯度結構鋁薄板成形的影響，本節在保證擠壓角度C為120°的前提下，模擬了開口圓角R在0.5 ～2.5 mm梯度結構鋁薄板成形的結果，其中材料流動速度如圖4所示，材料分流邊界由實線標出。

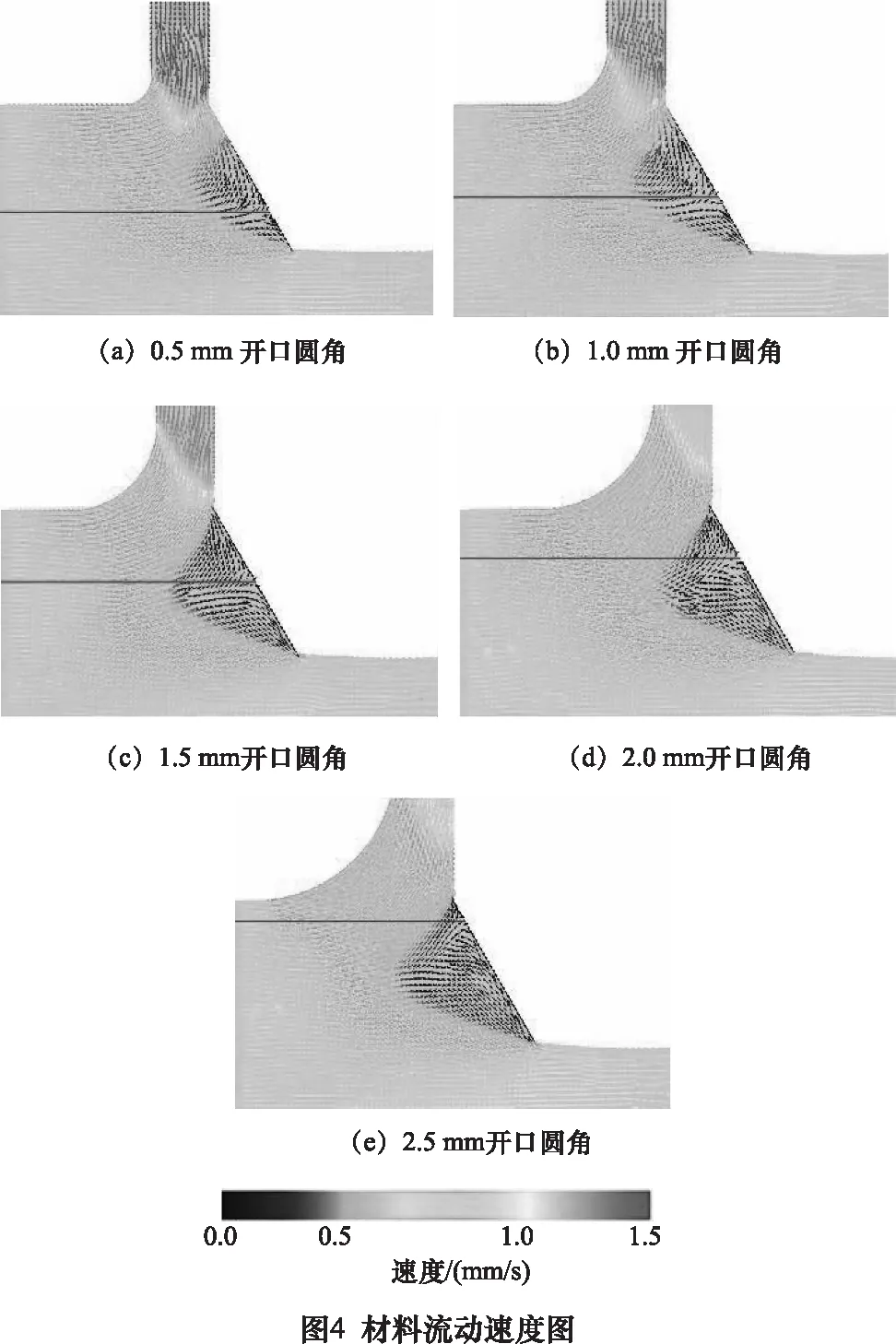
由圖5可以看出，隨著開口圓角R的增大，梯度結構鋁薄板的側向擠壓比x逐漸減小。

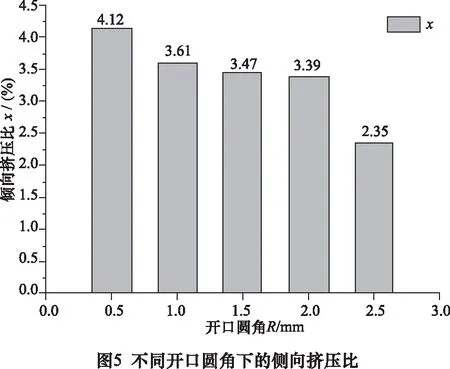
由圖4可知，這是因為當R為0.5 mm時，材料橫向流動阻力相對較大，開口擠出阻力相對較小，材料分流邊界位于區域2，且開口附近材料流動速度較快，故較多的材料從開口擠出，側向擠壓比x較大。當R從0.5 mm逐漸增大到2.5 mm時，材料橫向流動阻力逐漸減小，開口擠出阻力逐漸增大，材料分流邊界由區域2逐漸過渡到區域1，且開口附近材料流動速度也逐漸減慢，故較少的材料從開口擠出，側向擠壓比x逐漸減小。

3.1.2 開口圓角對鋁薄板等效應變的影響分析

對于開口圓角R在0.5～2.5 mm的模擬結果，其等效應變如圖6所示。分別測量開口附近擠出鋁薄板左右兩側的等效應變值，其結果如圖7所示。

由圖7可以看出，隨著開口圓角R的增大，梯度結構鋁薄板左側等效應變εL逐漸增大。當開口圓角R1.5 mm時，梯度結構鋁薄板右側等效應變εR隨R的增大而增大，當R1.5 mm時，εR隨R的增大而減小。當R為1.5 mm時，εR與εL之差最大。

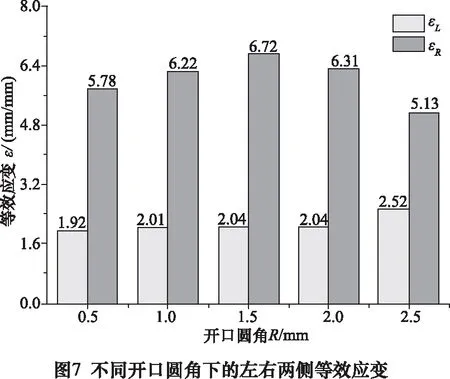
由圖4可知，這是因為對于薄板左側，當R從0.5 mm逐漸增大到2.5 mm時，圓角過渡作用逐漸增大，材料更加容易流入薄板左側，塞積現象較嚴重，晶粒之間相互作用較大，且開口附近材料流動速度逐漸減慢，與開口側壁摩擦作用較充分，故左側等效應變εL逐漸增大。然而，對于薄板右側，當R1.5 mm時，隨著R的增大，開口附近材料流動速度逐漸減慢，與開口側壁摩擦作用較充分，雖然材料分流邊界有所上移，但效果弱于摩擦作用，故εR逐漸增大。當R1.5 mm時，隨著R的增大，材料分流邊界由區域1與區域2的交界處逐漸上移到區域1頂部，流入薄板右側的材料減少，塞積現象較微弱，晶粒之間相互作用較小，雖然開口附近材料流動速度仍然減慢，但效果弱于晶粒之間相互作用，故εR逐漸減小。

3.2 擠壓角度對鋁薄板成形影響分析

為了分析擠壓角度對梯度結構鋁薄板成形的影響，本節在保證開口圓角R為1.5mm的前提下，模擬了擠壓角度C在100°～140°梯度結構鋁薄板成形的結果，其中材料流動速度如圖8所示，材料分流邊界由實線標出。

3.2.1 擠壓角度對鋁薄板側向擠壓比的影響分析

對于擠壓角度C在100°～140°的模擬結果，分別測量其擠出鋁薄板長度L0，并據式(2)計算相應的側向擠壓比x，結果如圖9所示。

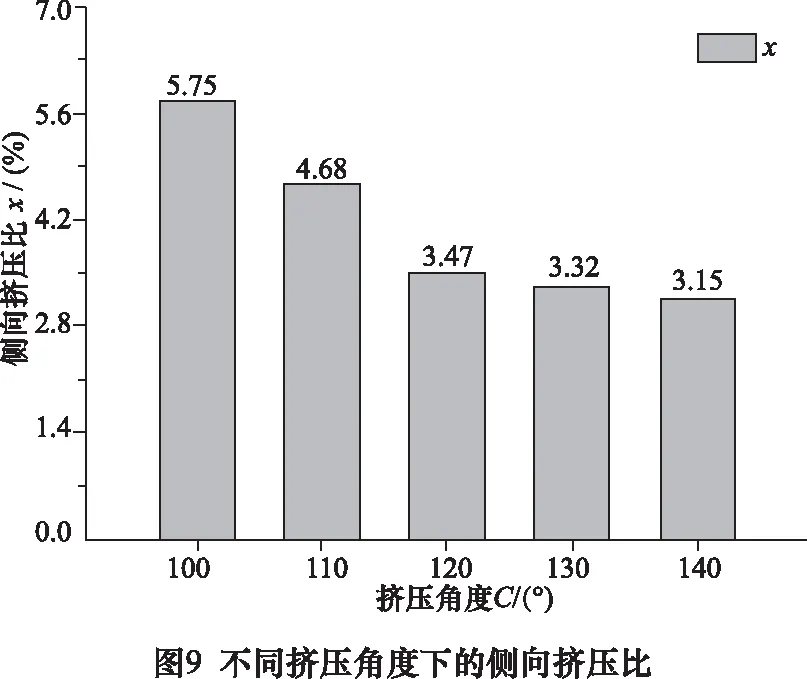
由圖9可以看出，隨著擠壓角度C的增大，梯度結構薄板側向擠壓比x逐漸減小。

由圖8可知，這是因為當C為100°或110°時，材料分流邊界位于區域2底部，且開口附近材料流動速度較快，故較多的材料從開口擠出，側向擠壓比x較大。當C為120°時，材料分流邊界迅速上移，位于區域1與區域2的交界處，且開口附近材料流動速度減慢，故從開口擠出的材料減少，側向擠壓比x減小。當C為130°或140°時，材料分流邊界再次迅速上移到區域1頂部，且開口附近材料流動速度減慢，故較少的材料從開口擠出，側向擠壓比x較小。由此可見，當C在110°和130°之間變化時，材料分流邊界上移速度很高，可作進一步研究。

3.2.2 擠壓角度對鋁薄板等效應變的影響分析

對于擠壓角度C在100°～140°的模擬結果，等效應變如圖10所示。分別測量開口附近擠出鋁薄板左右兩側的等效應變值，結果如圖11所示。

由圖11可以看出，隨著擠壓角度C的增大，梯度結構鋁薄板左側等效應變εL逐漸減小。當擠壓角度C120°時，梯度結構鋁薄板右側等效應變εR整體上隨R的增大而增大，當R120°時，εR隨R的增大而減小。當C為120°時，εR與εL之差最大。

由圖8可知，這是因為對于薄板左側，當C從100°逐漸增大到140°時，材料分流邊界由區域2底部逐漸上移到區域1頂部，從開口擠出的材料減少，塞積現象減弱，晶粒之間相互作用減小，雖然開口附近材料流動速度逐漸減慢，但效果弱于晶粒之間相互作用，故左側等效應變εL逐漸減小。然而，對于薄板右側，當C120°時，隨著C的增大，開口附近材料流動速度逐漸減慢，與開口側壁摩擦作用較為充分，雖然材料分流邊界有所上移，但效果弱于摩擦作用，故εR整體上逐漸增大。當C120°時，隨著C的增大，材料分流邊界迅速上移，從開口擠出的材料減少，塞積現象減弱，晶粒之間相互作用減小，雖然開口附近材料流動速度仍減慢，但效果弱于晶粒之間相互作用，故右側等效應變εR逐漸減小。

4 結語

本文采用控制變量法，對不同開口圓角R與擠壓角度C下梯度結構鋁薄板的成形進行仿真分析，所用材料模型與文獻[18]及[21]中的材料模型完全一致，且所得模擬結果與文獻[18]及[21]中的數值分析結果及實驗趨勢基本相符，故證明該模擬結果具有較高的可信度。最終，得出了R與C對梯度結構薄板側向擠壓比及等效應變的影響規律，總結如下：

(1)隨著R的增大，梯度結構鋁薄板側向擠壓比x逐漸減小，左側等效應變εL逐漸增大，右側等效應變εR呈現先增大后減小的趨勢。當R為1.5 mm時，εR與εL之差最大。

(2)隨著擠壓角度C的增大，梯度結構鋁薄板側向擠壓比x逐漸減小，左側等效應變εL逐漸減小，右側等效應變εR整體上呈現先增大后減小的趨勢。當C為120°時，εR與εL之差最大。

(3)在保證PFM模具其他結構不變的前提下，取R為1.5 mm及C為120°時，所制備鋁薄板的應變梯度最為明顯。