閉環控制DC/DC變換器帶恒功率負載的穩定性研究
尹英龍,劉寶泉
(陜西科技大學 電氣與控制工程學院,西安 710021)
在直流微電網中,電力電子變換器在電力系統的大規模應用[1-3],給電力系統引入了大量非線性負載,對電力系統的穩定性產生諸多不利影響[4]。恒功率負載作為一種典型的非線性負載[5],在DC/DC分布式系統以及大部分直流微電網的場景中占有越來越大的比例,尤其是當閉環控制的多個電力電子變換器級聯時,后級通常可以等效為前級的恒功率負載。
目前的穩定性研究以小信號擾動為主,利用小信號分析方法可以忽略系統中微小的非線性因素,對建立的模型線性化處理從而推導出穩定性判據,能夠解決平衡點附近的穩定性問題[6],但恒功率負載和電力電子變換器自身特性給系統帶來的非線性不可忽略。為了尋求對含恒功率負載的系統進行有效控制的方法,對其進行大信號下的穩定性分析尤為重要。在直流微網中,大信號穩定性是指系統受到大擾動時系統的穩定性[7],例如起動、負載突變以及系統中有非線性負載等工況[8-9]。
目前,針對大信號的穩定性分析主要有兩種方法,一是Lyapunov特征值法估計,將原系統狀態方程線性化后,通過系統雅克比矩陣的特征值來判斷系統在平衡點的穩定性,當特征值均有負實部時,該系統在平衡點處穩定,但該方法涉及多維矩陣的復雜計算,不便于實際的操作。第二種方法是利用混合勢函數理論,它是一種基于Lyapunov直接法的特殊分析方法[10],根據系統中元器件的能量關系,列寫能量方程,進一步計算出解析形式的穩定性判據。在電力系統中基于這一方法研究人員開展了大量工作并得到了諸多成果。文獻[11]利用混合勢函數結合驗證了無源控制下的燃料電池-超級電容器(FC-UC)系統的穩定性。文獻[12]利用混合勢函數對三相PWM整流器級聯DC/DC變換器系統(雙閉環系統)進行了大信號分析,得到大擾動下的穩定邊界(不等式),并進行了簡單的仿真驗證。文獻[13]使用混合勢函數推導了下垂控制的含CPL和LC濾波器的直流系統穩定性判據,并通過仿真驗證了該判據的有效性。文獻[14-16]利用混合勢函數理論分析了開環控制的電力電子變換器在大信號擾動下的穩定邊界,得到了解析形式的穩定性判據,為系統的設計提供了準則。文獻[17]利用混合勢函數理論對直流微電網級聯系統中恒功率負載和儲能單元充放電功率參數對穩定性的影響進行研究并得到了穩定性判據。文獻[18-19]將級聯系統中負載變流器等效為恒功率負載,基于回轉器理論建立DC/DC變換器統一的大信號模型,并推導了基于該模型的混合勢函數穩定性判據,定量地分析了控制器參數對電流控制型BUCK/BOOST變流器穩定性的影響。文獻[20-22]利用混合勢函數的方法建立了雙級LC濾波器和4種阻尼濾波器的系統大信號模型,并推導各種濾波器對大擾動下的穩定性的影響。文獻[23]假設電流內環跟蹤電壓外環實時變化,簡化了電壓電流雙閉環的等效電路并在此基礎上利用混合勢函數方法分析穩定性并得出穩定性判據。
當前研究主要以開環為主,而閉環控制型(VMC)的電力電子裝置還沒有過多的涉及。本文以BUCK變換器為研究對象,控制方法采用電壓電流雙閉環,控制器選用比例積分控制器,建立了大信號平均模型,列寫了系統的混合勢函數,得到了大信號穩定的充分條件;進一步利用這一條件設計系統參數,得到漸進穩定域;并通過構造能量函數,利用Lyapunov穩定性判據驗證了穩定域的存在性。最后,通過仿真驗證了所求穩定運行條件的合理性。
1 閉環控制BUCK電路的大信號模型
根據圖1所示BUCK電路的簡化結構,設占空比為D,恒功率負載功率為P0,輸入電壓為U1可以得到BUCK電路帶CPL狀況下的大信號平均模型:
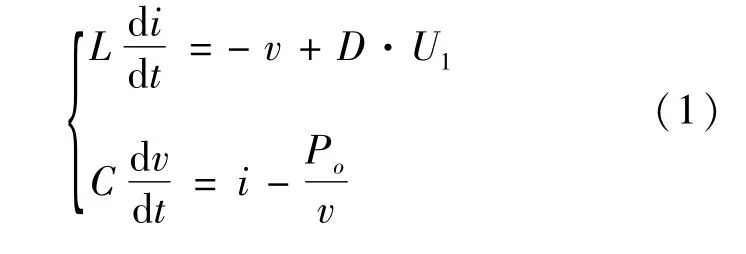
BUCK電路采用電壓電流雙閉環控制,設電壓外環的比例系數kvp,積分系數kvi,參考電壓為vref,電流內環的比例系數kip,積分系數kii,PWM比較器配置鋸齒波幅值vs=1,電路如圖2所示。
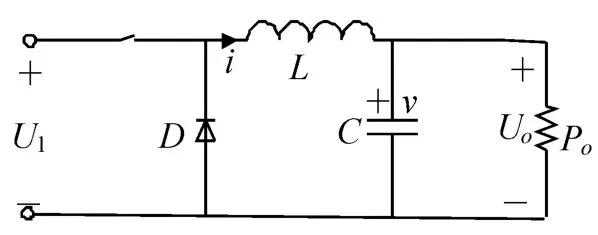
圖1 BUCK變換器簡化電路圖
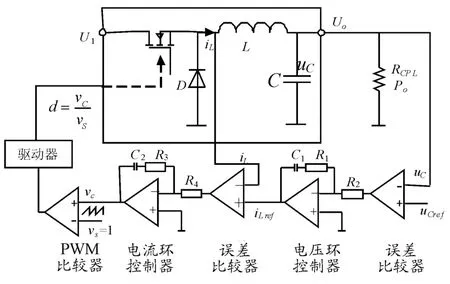
圖2 帶CPL的雙閉環控制BUCK變換器電路圖
電壓電流雙閉環控制建立了電感電流與占空比的關系,有
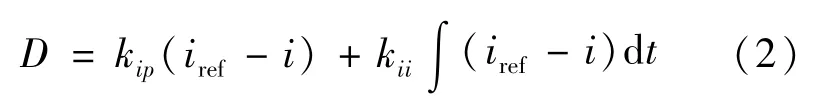
根據電壓環和電流環的連接關系,有
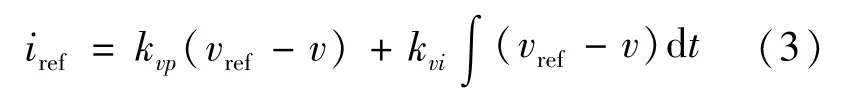
則電壓閉環控制的占空比D可以表示為
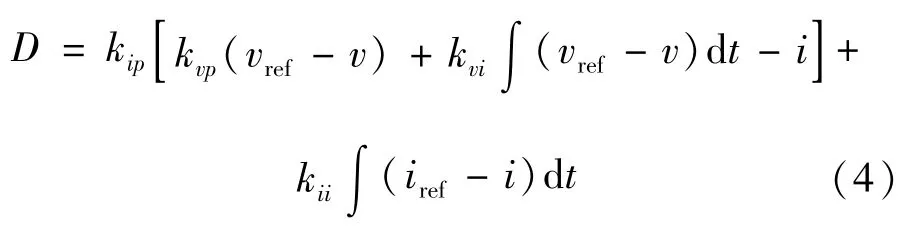
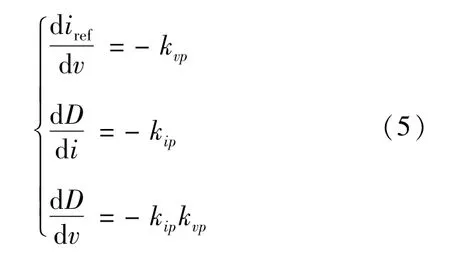
則電壓電流雙閉環控制下的占空比D可以改寫為:
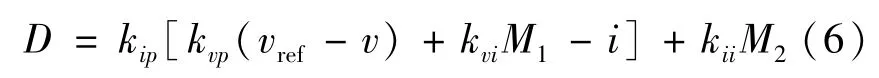
2 閉環控制BUCK 電路的混合勢函數模型
2.1 混合勢函數理論概述
1964年R.K.BRAYTON和J.K.MOSER提出了一種非線性網絡的理論,這是混合勢函數理論首次用于電力系統的穩定性分析。這種方法從能量的角度出發,結合Lyapunov穩定性分析方法,對滿足式(7)的網絡求解大信號穩定充分條件及具體的大信號漸進穩定域。
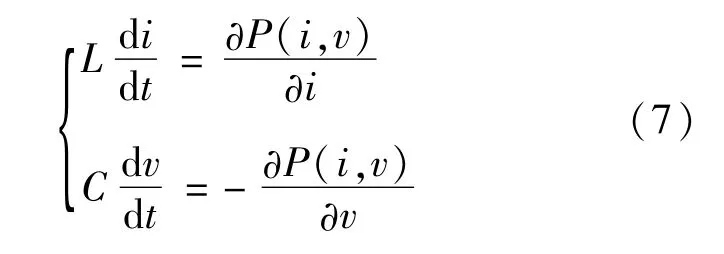
首先要列寫電路的混合勢函數P(i,v),它是由電流勢函數A(i)、電壓勢函數B(v)以及由于電路拓撲引起的能量變化(i,γv-α)3部分組成,即:
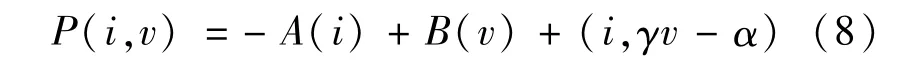
根據式(8),分別求出P(i,v)中電流勢函數和電壓勢函數對電感電流和電容電壓的二階導數Aii和Bvv,進而求解最小特征值λ1和λ2分別為:
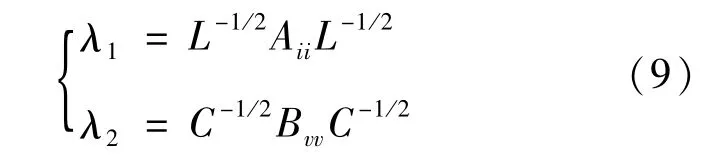
由此可以得到系統在大信號擾動下穩定的充分條件為λ1+λ2>0,設混合勢函數關于電感電流和電容電壓的一階偏導數為Pi和Pv,進一步構造Lyapunov能量函數P*(i,v)為

再求出能量函數對時間的導數d P*/d t,利用Lyapunov第二方法,找到使P*正定、d P*/d t負定的區域(i,v),即為系統在大信號下的漸進穩定域。
2.2 閉環控制BUCK變換器的混合勢函數
由電路中所有非儲能元件可以列寫出電流勢函數,若元件不能直接寫出電流勢函數,可以列寫電壓勢函數。圖2中所示BUCK電路中所有非儲能元件包括電壓源U1和恒功率負載CPL。其中恒功率負載的額定功率是P0,則電流勢函數可以記作P(i)。
電路中無電阻元件,開關前后的電源可以近似等效為受控電壓源,所有非儲能元件可以用電流勢函數表示:
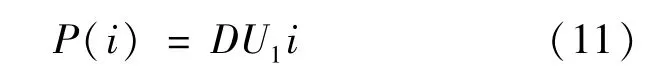
恒功率負載Po的電流勢函數轉化為電壓勢函數:
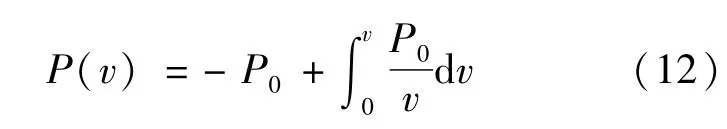
電容C的能量:
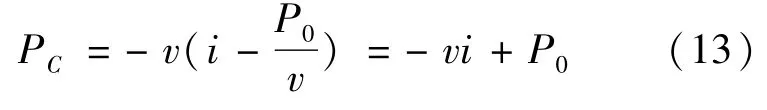
混合勢函數P(i,v)為式(11)~(13)的和,求和整理后結果如下:
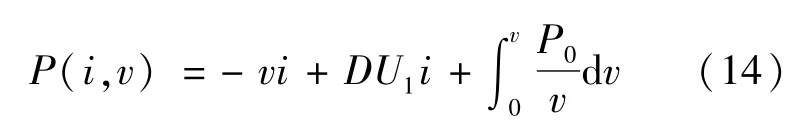
將所列寫的P(i,v)代入式(7)檢驗,混合勢函數列寫正確。進一步將式(6)代入式(14),即可得到閉環控制的BUCK變換器帶CPL的混合勢函數:
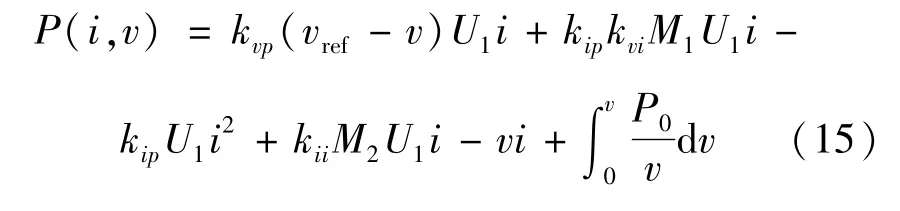
3 閉環控制BUCK電路穩定性分析
3.1 閉環系統大信號穩定的充分條件
設A(i)、B(v)和(i,γv-α)分別為式(14)中的電流勢函數、電壓勢函數和其他部分,有
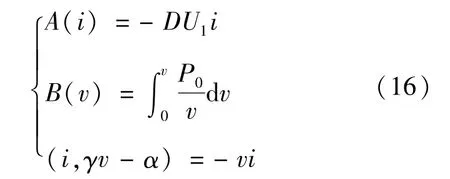
設A(i)和B(v)對電感電流的二階偏導數分別為Aii(i)和Bvv(v),有
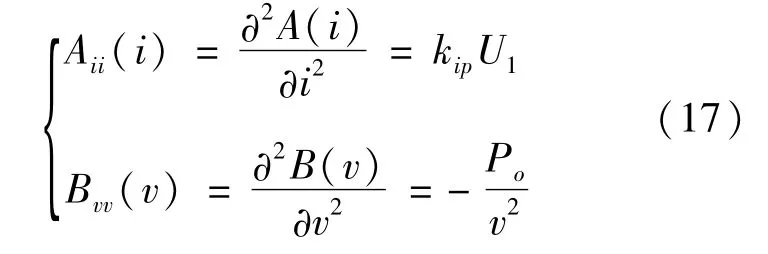
設矩陣L-1/2Aii(i)L-1/2和C-1/2Bvv(v)C-1/2的最小特征根為λ1和λ2,有
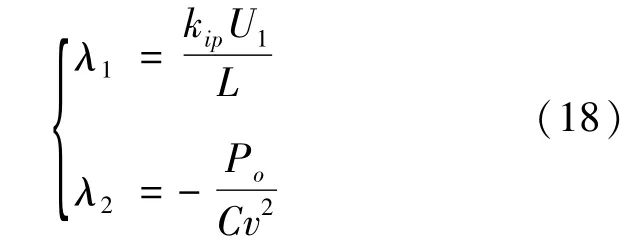
大信號擾動下,要該變換器穩定工作,需要λ1和λ2滿足λ1+λ2>0,即
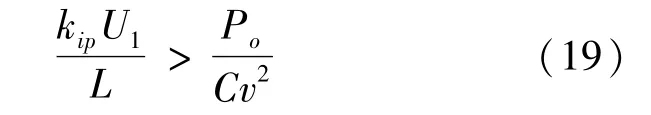
由恒功率負載的性質,有
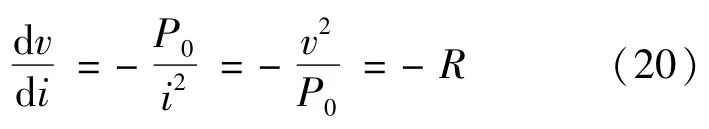
又有系統穩態平衡點為(UL,IL),恒功率負載滿足-RL=-UL/IL,則大信號穩定判據式(20)可以改寫為
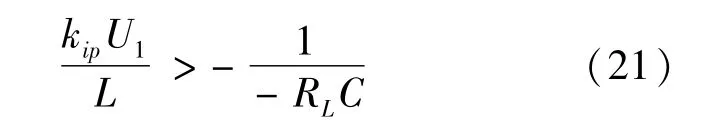
3.2 閉環系統的漸進穩定域
基于式(21)所示的大信號穩定判據,對圖2所示系統模型進行參數設計,具體取值如表1所示。
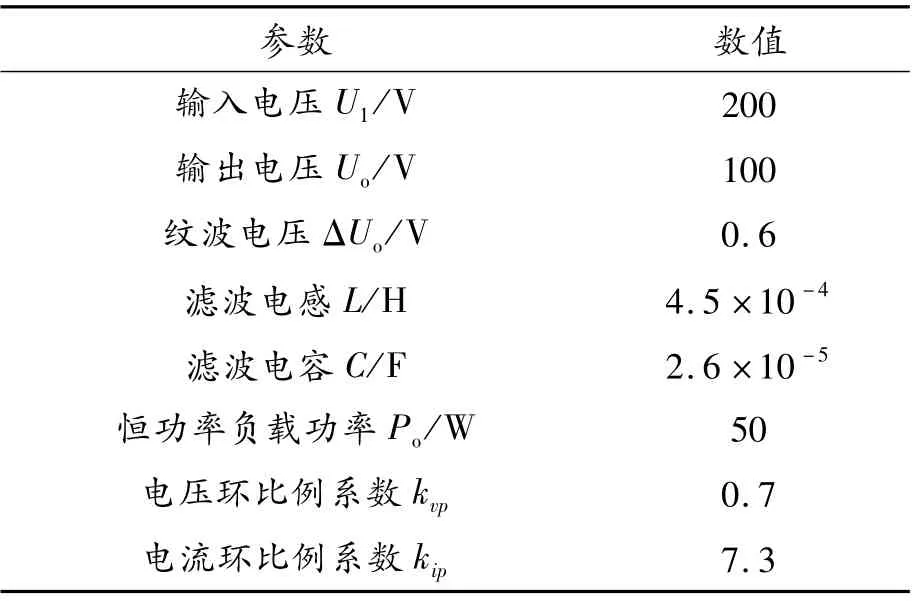
表1 200 V/100 V BUCK電路電壓閉環部分參數
根據第2節構造Lyapunov能量函數的方法,先求解Pi和Pv,有
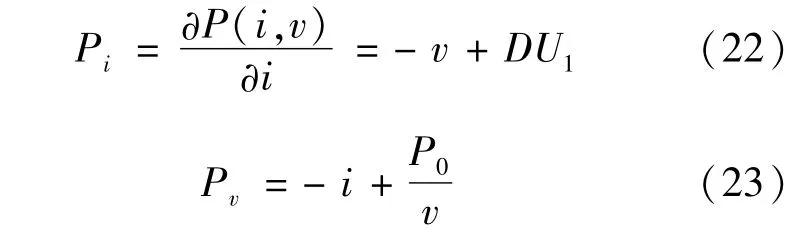
下面構造Lyapunov能量函數P*,并在能量函數的基礎上對時間t求導得到d P*(i,v)/d t:
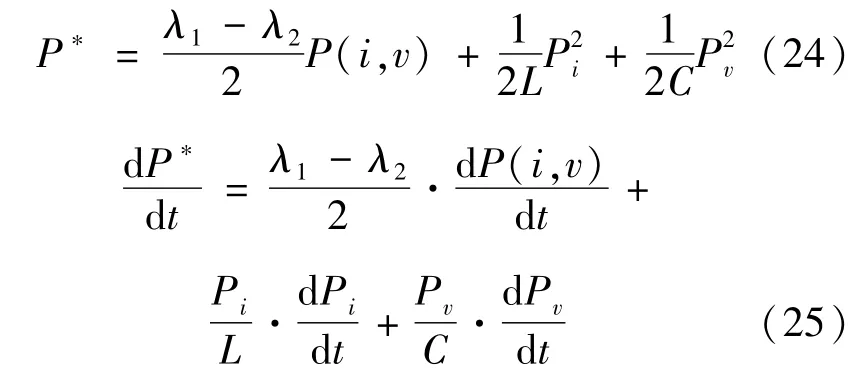
當P*(i,v)正定、d P*(i,v)/d t負定時,可以推得系統的漸進穩定域。以200 V/100 V BUCK變換器為例,把表1的參數代入式(24)(25)中計算,應用Matlab繪圖工具分別繪制電壓閉環條件下的P*(i,v)及d P*(i,v)/d t隨電感電流i、電容電壓v的三維曲線圖,分別如圖3、4所示。
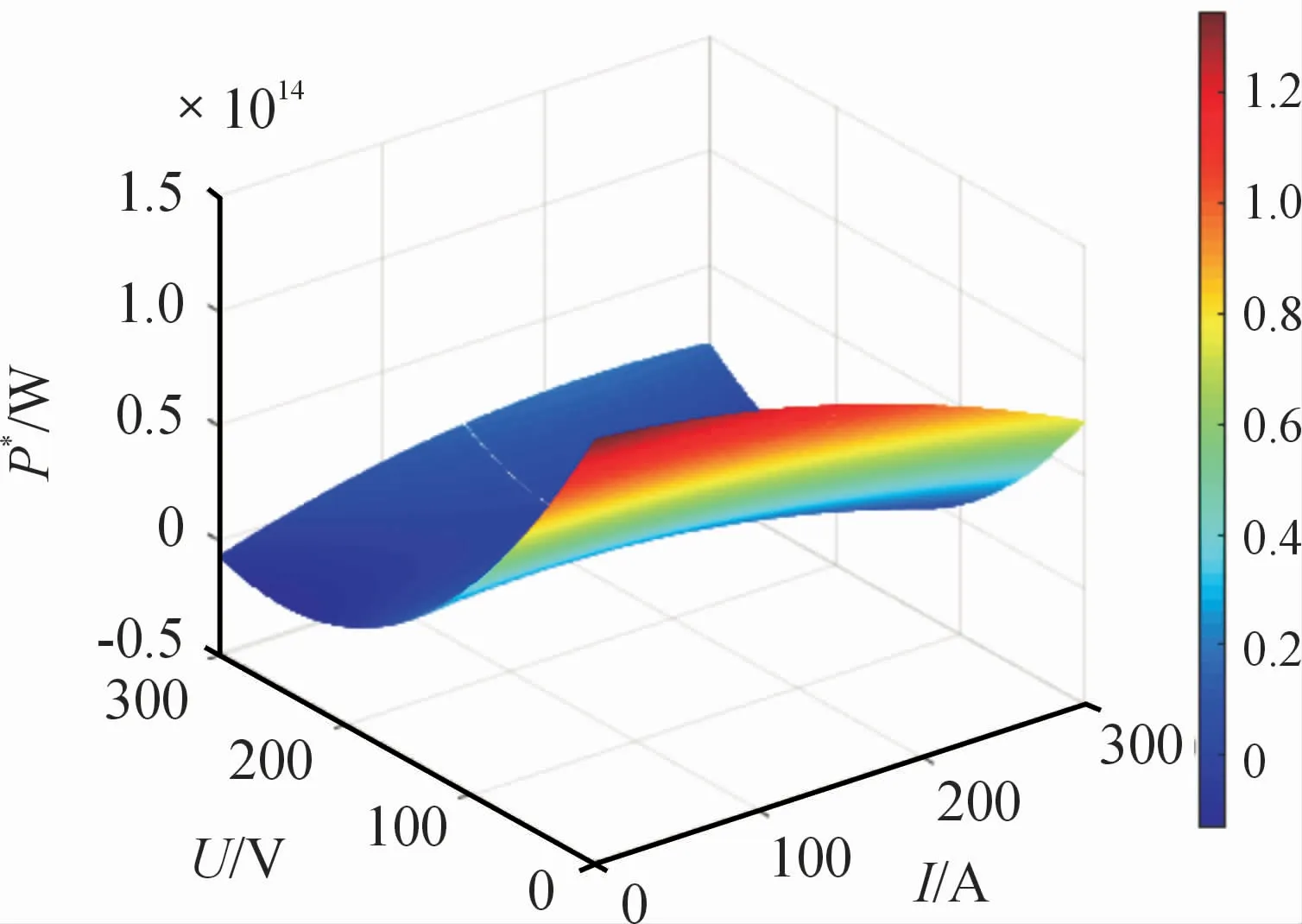
圖3 Lyapunov能量函數P*(i,v)三維圖
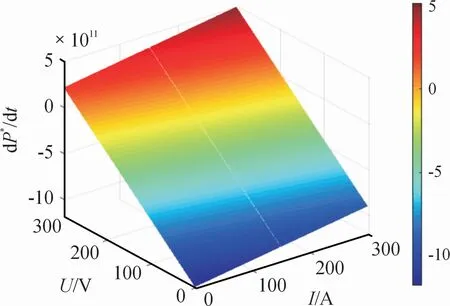
圖4 d P*(i,v)/d t三維圖
從圖中可以看出:存在著同時滿足P*(i,v)在P*=0平面以上和d P*(i,v)/d t在d P*/d t=0平面以下2個條件的區域,找到同時滿足2個條件的區域在i-v平面上的投影,即為該系統的漸進穩定域。
該系統在進行電能轉換時的漸進穩定域可以表示為
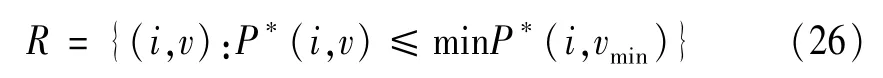
根據式(26),可以繪制系統的漸進穩定域,穩態工作點(100 V,5 A)包含在穩定域中,如圖5所示。
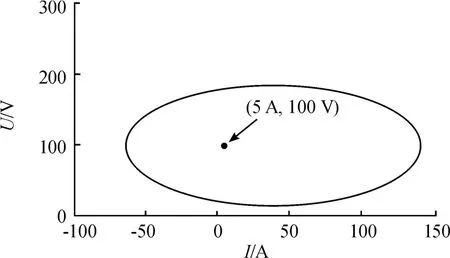
圖5 系統漸進穩定域示意圖
4 仿真驗證
本文主要采用Matlab/Simulink元件庫搭建雙閉環控制的BUCK電路帶恒功率負載仿真模型,具體如圖6所示,其中恒功率負載(CPL)模塊由含受控電流源單端口的電路模擬。

圖6 帶恒功率負載的BUCK電路仿真模型
利用表1中的電壓電流雙閉環控制的BUCK電路系統參數,對所求充分性條件的合理性進行仿真驗證,如圖7所示。先改變恒功率負載的功率取值,取滿足充分條件的兩組功率值P0=200 W(圖(a))和P0=500 W(圖(b)),該系統電壓在短暫一段時間振蕩后能夠穩定在100 V輸出;再取超出穩定條件的功率值(P0=5 kW)仿真,如圖8所示,系統電壓在不斷大幅振蕩,無法達到給定的輸出電壓值。
進一步對滿足充分條件的系統進行加載實驗,驗證大信號擾動下系統的穩定性。在帶恒功率負載為500 W 和800W 的系統穩定運行后分別突加10Ω的負載,如圖9所示,電壓值均在加載之后短暫波動,很快恢復到期望的輸出電壓值100 V,說明恒壓負載的大信號擾動下系統能夠穩定運行。再對帶恒功率負載Po=1 kW 的系統進行負載功率階躍的仿真,如圖10所示,在穩定運行后分別加載至2 kW 和3 kW,電壓值在短暫波動后迅速回到100 V,說明在功率突增的大信號擾動下,系統仍能穩定運行。
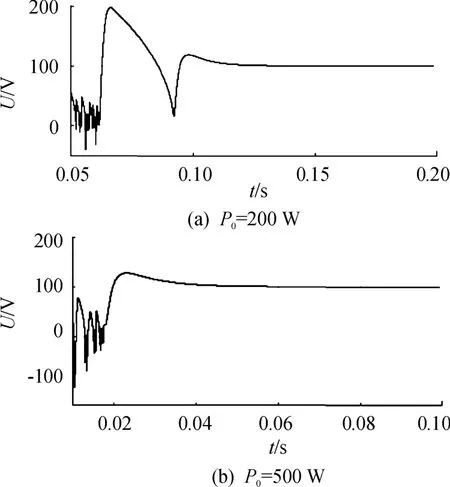
圖7 恒功率負載滿足充分條件時的電壓波形
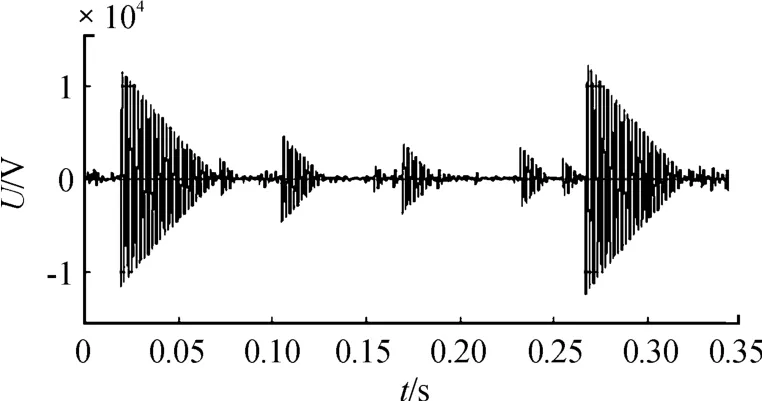
圖8 恒功率負載不滿足充分條件時的電壓波形
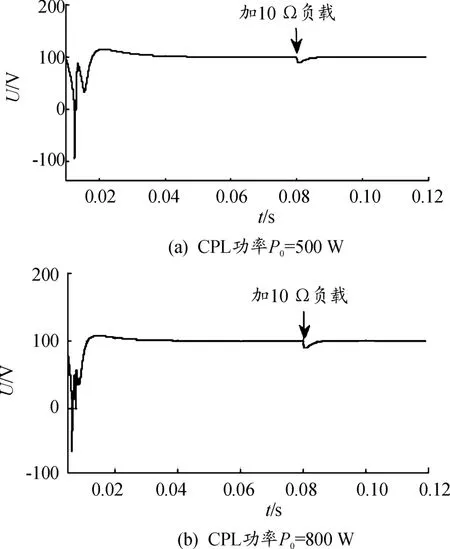
圖9 穩定運行后突加電阻負載的電壓波形

圖10 P0=1 kW 穩定運行后突加恒功率負載的電壓波形
5 結束語
本文基于大信號擾動的穩定性研究閉環系統涉及不多,以雙閉環控制的BUCK變換器帶恒功率負載系統為研究對象,利用混合勢函數的理論,得到了系統穩定的充分條件。該條件與恒功率負載的負阻抗特性、電流環的比例系數以及系統的電感電容參數均有關,且該條件為系統的參數設計提供了依據。設計的系統可以進一步構造能量函數,通過Lyapunov穩定性判據推導漸進穩定域。該穩定域的存在性表明滿足充分條件的系統在大信號擾動下可以穩定運行,仿真驗證了該條件的正確性。

