近鄰同步聚類模型與指數衰減加權同步聚類模型的比較與分析

陳新泉,周靈晶，戴家樹，周 祺

(1.安徽工程大學 計算機與信息學院，安徽 蕪湖 241000；2.安徽工程大學 教育工會，安徽 蕪湖 241000)

作為統計學中多元統計分析方法的一種重要技術，聚類分析試圖發現未知數據中的內在結構或分布規律。在機器學習中，聚類被稱為無監督學習，指的是試圖發現無標記數據中的內在分布結構，讓劃分后的簇表現出數據的自然結構特點。聚類可以讓缺乏先驗信息的數據集獲得其內在的分布結構(聚類的數目、大小、分布位置及空間結構等信息)，進而為半監督學習、監督學習、數據壓縮等一些后續操作提供一定的輔助信息。通常，同一聚類中的數據應該比不同聚類間的數據更為相似，不同聚類間的數據應該具有較大的差異。聚類在許多領域都有應用，如：心理學和其他社會科學、生物學、統計學、模式識別、信息檢索、機器學習和數據挖掘。

聚類分析屬于一個交叉研究領域，它融合了多個學科的方法和技術。Qlan Wei-ning等從多個角度分析了現有的許多聚類算法，給出了一些優缺點比較分析結果。Johannes Grabmeier等從數據挖掘的角度(如相似度的定義、相關的優化標準等)分析了許多聚類算法。Arabie和Hubert的專著是早期聚類分析領域的一本很有價值的參考文獻。Jain等對一些經典聚類算法進行了很好地比較與分析，這是聚類分析領域早期一篇經典的綜述文獻。2000年后，Rui Xu等和Anil K.Jain對聚類算法分別做了較為全新的綜述分析。

傳統的聚類算法一般可分為基于劃分的聚類方法、層次聚類方法、密度聚類方法、網格聚類方法、模型聚類方法、圖聚類方法等。近年來，量子聚類方法、譜聚類方法、粒度聚類方法、概率圖聚類方法、同步聚類方法等也流行起來。

B?hm等于2010年第一次將自然界中普通存在的同步現象引入聚類分析領域，在國際頂級會議KDD(Knowledge Discovery and Data Mining)上發表了第一篇同步聚類算法論文。這篇開拓性論文首先將Kuramoto模型進行了適當地推廣，得到可應用于聚類算法中的擴展Kuramoto模型，提出了(Synchronization clustering，Sync)聚類算法。接著作者還將最小描述長度原理應用于Sync算法中，提出了一種參數的自動優化方法。基于同步模型的聚類算法可以緩解聚類分析和噪聲檢測在傳統數據上的某些難題，它具有動態性、局部性及多尺度分析等特性，可以在一定程度上解決大規模數據的聚類分析所面臨的困難。自此之后，新型的基于同步模型的聚類算法形成了一個研究熱潮。

自Sync算法發表后，吸引了一些研究人員的注意。近幾年，邵俊明等從多個角度研究基于同步模型的數據挖掘方法，發表了多篇高水平論文。例如，文獻[10]提出了一種新穎的孤立點檢測算法。文獻[11]提出了一種新穎有效的高效子空間聚類算法(arbitrarily ORiented Synchronized Clusters，ORSC)。文獻[12]提出了一種基于同步模型和最小描述長度原理的新穎的動態層次聚類算法(hierarchical Synchronization clustering，hSync)，文獻[13]提出了一種可以發現復雜圖的內在模式的新穎的圖聚類算法(Robust Synchronization-based Graph Clustering，RSGC)。文獻[14]提出了一種用于檢測概念漂移的基于原型學習的數據流挖掘算法。黃健斌等在文獻[8]的基礎上，提出了一種層次型的同步聚類算法(Synchronization-based Hierarchical Clustering，SHC)。2017年，陳新泉找到了另外一種更為有效的同步聚類模型—Vicsek模型的線性版本。在將這種Vicsek模型的線性版本應用到聚類中后，發表了基于該模型的ESynC(Effective Synchronization Clustering)算法。杭文龍等基于重力學中的中心力優化方法，提出了一種局部同步聚類算法(Gravitational Synchronization clustering，G-Sync)。陳新泉在文獻[8]的基礎上，提出了基于三種空間索引結構的快速同步聚類算法(Fast Synchronization Clustering，FSynC)。FSynC算法中的兩種參數型方法在某些情況下可得到O(dnlogn)的時間代價。這幾篇較新的同步聚類論文分別從不同的角度拓展了同步聚類算法的研究。

1 基本概念

設數據集

S

={

x

,

x

,…,

x

()}分布在

d

維有序屬性空間(

A

×

A

×…×

A

)的某個有限區域內。為更好地描述研究算法，先給出幾個基本定義。

定義

1

數據集

S

中的點

x

()(

i

=1,…,

n

)的

δ

近鄰點集

δ

(

x

())定義為：

δ

(

x

())={

x

|0<

dis

(

x

,

x

())≤

δ

,

x

∈

S

,

x

≠

x

()}。

(1)

式中，

dis

(

x

,

x

())為

S

中的兩個不同點

x

和

x

()的相異性度量，

δ

是一個預先設定的閾值參數。定義1的實質意義是：

δ

(

x

())是從中選取與點

x

()相距不超過

δ

“距離”的其他點所構成的集合。

定義

2應用到聚類中的擴展的Kuramoto模型定義為：

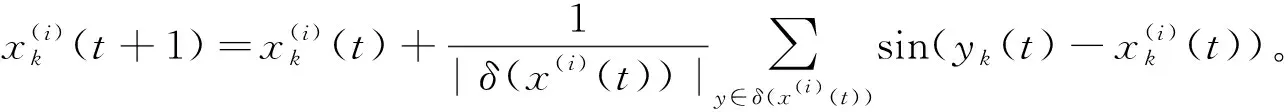
(2)

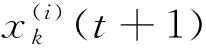
定義

316應用到聚類中的

Vicsek

簡化模型定義為：

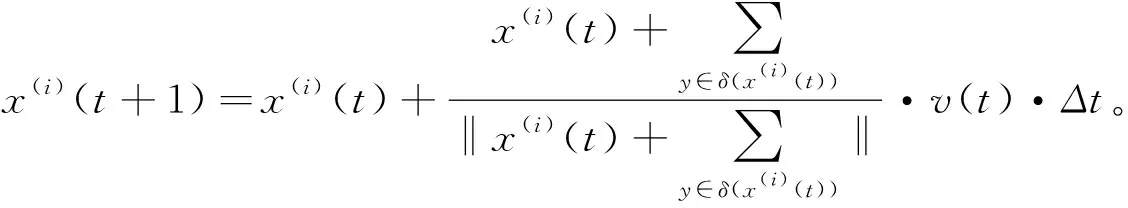
(3)

式中，

x

()(

t

+1)表示點

x

()在第

t

個同步后的更新位置；

v

(

t

)表示第

t

個同步時的移動速度；

v

(

t

)·

Δt

表示第

t

個同步的移動路徑長度。在一些基于Vicsek模型的多agent系統中，

v

(

t

)是個常量。通過一些仿真實驗的觀察，當

v

(

t

)是常量時，基于式(3)的Vicsek模型的原始版本不能很好地應用到聚類中，所以將Vicsek模型的另外一種有效版本應用到聚類中。

(4)

式中，

x

()(

t

+1)表示點

x

()在第

t

個同步后的更新位置。式(4)與Mean Shift聚類算法中的下一個搜索位置的計算公式相似。從中我們可以看出，點

x

()的更新位置就是點

x

()及它的

δ

近鄰點集

δ

(

x

())的均值位置。式(4)還可以被改寫為：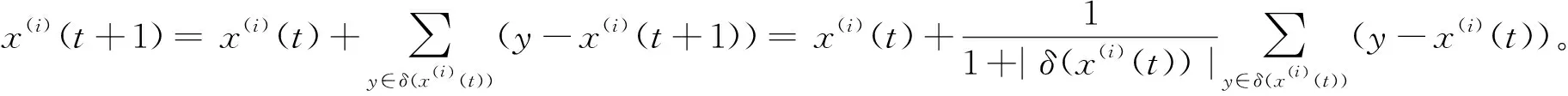

(5)

式(5)與式(2)在外形方面有點相似，但它們有著本質的區別。我們可以看到，式(2)所表示的更新模型是非線性的，而式(4)與式(5)的更新模型是線性的。

基于萬有引力定律和物理學中普遍存在的指數衰減規律，我們提出下面的三種指數衰減加權同步模型。前兩種模型是在全局范圍內進行迭代計算，后一種是在

δ

近鄰范圍內進行迭代計算。

定義

5

應用到聚類中的第一種指數衰減加權同步模型定義為：

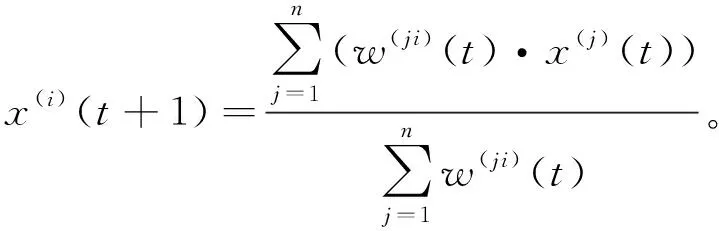
(6)

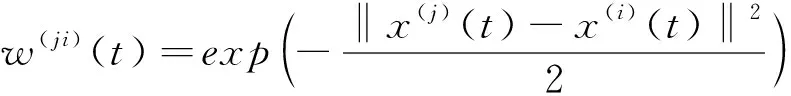
定義

6

應用到聚類中的第二種指數衰減加權同步模型定義為：

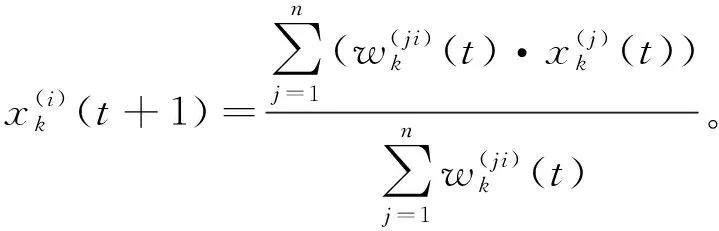
(7)

定義

7

應用到聚類中的

δ

近鄰指數衰減加權同步模型定義為：

(8)

定義

8 數據集

S

={

x

,

x

,…,

x

()}在經歷了

T

步的同步聚類后穩定下來，表示為

S

(

T

)={

x

(

T

),…,

x

()(

T

)}。設從

S

(

T

)可獲得

K

個聚類和

K

個孤立點，

K

=

K

+

K

。

S

(

T

)的聚類穩定點集記為

C

={

c

,…,

c

()}，其中

c

()是第

j

個聚類區域的穩定標記位置。如果

x

()(

T

)滿足式(9)，則點

x

()判為屬于第

j

個聚類區域。

dis

(

c

(),

x

()(

T

))<

ε

。

(9)

式(9)中的參數

ε

與算法中的迭代退出閾值參數

ε

相同，是一個非常小的實數。如果第

j

個聚類區域包含了

n

個數據點，則這

n

個數據點在原始數據集

S

={

x

,…,

x

()}中的均值位置

m

()與第

j

個聚類穩定點位置

c

()之間的距離表示為

dis

(

c

(),

m

())，則

K

個聚類區域的穩定位置與

K

個聚類區域的均值位置差異值定義為：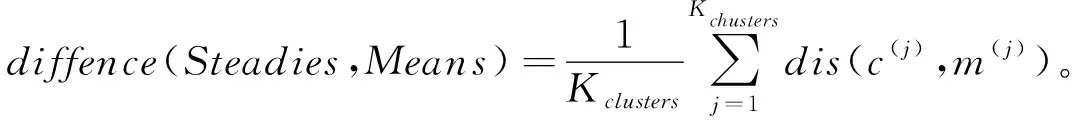

(10)

顯然，式(10)所表示的這個指標可度量同步聚類后聚類區域的穩定位置與均值位置的平均差異。

定義

9

互信息(Mutual Information,MI)。根據香農信息論，兩個離散隨機變量

X

和

Y

的互信息定義為：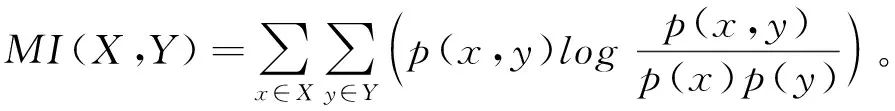

(11)

式中，

p

(

x

,

y

)是兩個隨機變量

X

和

Y

的聯合概率密度分布函數，

p

(

x

)是隨機變量

X

的邊緣概率密度分布函數，

p

(

y

)亦然。

定義

10 正規化互信息(Normalized Mutual Information,NMI)。兩個聚類結果

X

和

Y

的正規化互信息定義為：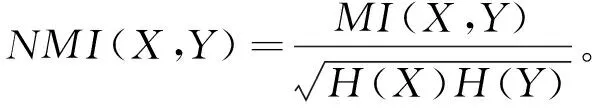

(12)

式中，

MI

(

X

,

Y

)是兩個聚類結果

X

和

Y

的互信息，

H

(

X

)是聚類結果

X

的信息熵，

H

(

Y

)亦然。

定義

11

調整互信息(Adjusted Mutual Information,AMI)。兩個聚類結果

X

和

Y

的調整互信息定義為：

(13)

式中，

MI

(

X

,

Y

)，

H

(

X

)，

H

(

Y

)的含義與上面相同，

E

{

MI

(

X

,

Y

)}是兩個聚類結果

X

和

Y

的互信息的數學期望。

定義

12

調整變信息(Adjusted Variation Information,AVI)。兩個聚類結果

X

和

Y

的調整變信息定義為：

(14)

式中，

MI

(

X

,

Y

)，

H

(

X

)，

H

(

Y

)，

E

{

MI

(

X

,

Y

)}的含義與上面相同。當聚類結果

X

和

Y

完全一致時，

NMI

，

AMI

和

AVI

取值為1。當聚類結果

X

和

Y

的互信息等于它們的期望時，

AMI

和

AVI

取值為0；當聚類結果

X

和

Y

的分布相互獨立時，

NMI

取值為0。

2 基于同步模型的聚類算法

B?hm等提出的Sync算法，Chen提出的ESynC算法是2.1節中基于近鄰同步模型的聚類算法的兩個典型代表，基于指數衰減加權同步模型的聚類算法將在2.2節中予以介紹。

2.1 基于近鄰同步模型的聚類算法

基于近鄰同步模型的聚類算法是一種在

δ

近鄰范圍內進行動態同步迭代的聚類算法框架，具體表述如下：

算法1:基于近鄰同步模型的聚類算法

輸入：數據點集

S

={

x

,…,

x

()}，距離相異性度量

dis

(·,·)，近鄰閾值參數

δ

，迭代退出閾值參數

ε

；輸出：數據點集

S

的聚類結果，可以采用數據點的聚類歸屬標記數組

FinCluResult

[1…

n

]；1:迭代步

t

初始化為0，即：

t

←0；2:for

i

=1,2,…,

n

do;3:

x

()(

t

)←

x

()

4:end for

5:while(

S

(

t

)={

x

(

t

),

x

(

t

),…,

x

()(

t

)}仍在同步移動中)do6: for

i

=1,2,…,

n

do7: 根據式(1)為數據點

x

()構造它的

δ

近鄰點集

δ

(

x

())；8: 根據定義2，或定義3，或定義4，或定義7計算

x

()(

t

)同步后的更新值

x

()(

t

+1)；

9: end for

11: if(

mse

(

S

(

t

),

S

(

t

+1))<

ε

)then

12: 這個動態的同步聚類過程收斂了，可以從while循環中退出來；

13: else

14: 迭代步

t

增加一步，即：

t

++，然后進入下一次while循環；

15: end if

16:end while

17:將退出while循環的

t

值賦給同步總次數

T

，此時可得到數據點集

S

同步后的收斂結果集

S

(

T

)={

x

(

T

),

x

(

T

),…,

x

()(

T

)}；18:在

S

(

T

)中，那些代表一些數據點的穩定位置可看作是聚類中心，那些只代表一個或幾個點的穩定位置可看作是孤立點的最終同步位置。根據

S

(

T

)={

x

(

T

),

x

(

T

),…,

x

()(

T

)}很容易得到一個由若干個穩定點或孤立點構成的自然聚類簇，從而構造出

FinCluResult

[1..

n

]。備注：在算法1的第8步中，如果采用定義2來計算

x

()(

t

)同步后的更新值

x

()(

t

+1)，就是B?hm等提出的Sync算法；如果采用定義4來計算

x

()(

t

)同步后的更新值

x

()(

t

+1)，就是Chen提出的ESynC算法；定義3的同步模型在文獻[16]中已有幾個對照實驗；如果采用定義7來計算

x

()(

t

)同步后的更新值

x

()(

t

+1)，則會得到一種同步聚類算法。

2.2 基于指數衰減加權同步模型的聚類算法

基于指數衰減加權同步模型是一種在全局范圍內進行動態同步迭代的聚類算法框架，具體表述如下：

算法2:基于指數衰減加權同步模型的聚類算法

輸入：數據點集

S

={

x

,…,

x

()}，距離相異性度量

dis

(·,·)，迭代退出閾值參數

ε

；輸出：數據點集

S

的聚類結果，可以采用數據點的聚類歸屬標記數組

FinCluResult

[1..

n

]；1:迭代步

t

初始化為0，即：

t

←0；2:for

i

=1,2,…,

n

do3:

x

()(

t

)←

x

();

4:end for

5:while(

S

(

t

)={

x

(

t

),

x

(

t

),…,

x

()(

t

)}仍在同步移動中)do6: for

i

=1,2,…,

n

do7: 根據定義5，或定義6計算

x

()(

t

)同步后的更新值

x

()(

t

+1)；

8: end for

10: if(

mse

(

S

(

t

),

S

(

t

+1))<

ε

)then

11: 這個動態的同步聚類過程收斂了，可以從while循環中退出來；

12:

else

13: 迭代步

t

增加一步，即：

t

++，然后進入下一次while循環；

14: end if

15:end while

16:將退出while循環的

t

值賦給同步總次數

T

，此時可得到數據點集

S

同步后的收斂結果集

S

(

T

)={

x

(

T

),

x

(

T

),…,

x

()(

T

)}；17:在

S

(

T

)中，那些代表一些數據點的穩定位置可看作是聚類中心，那些只代表一個或幾個點的穩定位置可看作是孤立點的最終同步位置。根據

S

(

T

)={

x

(

T

),

x

(

T

),…,

x

()(

T

)}很容易得到一個由若干個穩定點或孤立點構成的自然聚類簇，從而構造出

FinCluResult

[1..

n

]。備注：在算法2的第7步中，如果采用定義5來計算

x

()(

t

)同步后的更新值

x

()(

t

+1)，會得到一種同步聚類算法；如果采用定義6來計算

x

()(

t

)同步后的更新值

x

()(

t

+1)，則會得到另外一種同步聚類算法。

2.3 算法的復雜度分析

(1)算法1的復雜度分析。在算法1中，步1只需要

O

(1)的時間代價，步2到步4需要

O

(

n

)的時間代價。步5需要

O

(

T

)的時間代價。在步7中，如果采用簡單的全范圍蠻力判斷方法，為數據點

x

()(

i

=1,…,

n

)構造它的

δ

近鄰點集

δ

(

x

())需要

Time

=

O

(

dn

)。當數據集的維數較小時，通過為數據點集構造空間索引結構的方法，可以取得

O

(

d

log

n

)的時間代價。在步8中，計算

x

()(

t

)(

i

=1,…,

n

)同步后的更新值

x

()(

t

+1)需要

Time

=

O

(

d

·|

δ

(

x

())|)。所以步6到步10最多需要

O

(

dn

)的時間代價。步10需要

O

(

dn

)的時間代價。步11到步15只需要

O

(1)的時間代價。步17只需要

O

(1)的時間代價。步18需要

O

(

dnK

)的時間代價，其中

K

是聚類數和孤立點數之和，一般有

K

?

n

。根據B?hm等和我們的分析，算法1未采用空間索引結構時的時間代價為

Time

=

O

(

Tdn

)；算法1在低維數據集中，采用有效的空間索引結構時的時間代價為

Time

=

O

(

Tdn

log

n

)。(2)算法2的復雜度分析。算法2中的步1，步2到步4，步5的時間代價與算法1相同。在步6到步8中，使用定義5來計算

w

()(

t

)(

i

,

j

=1,…,

n

)需要

Time

=

O

(

d

)，計算

x

()(

t

)(

i

=1,…,

n

)同步后的更新值

x

()(

t

+1)需要

Time

=

O

(

dn

)；使用定義6來計算

w

()(

t

)(

i

,

j

=1,…,

n

;

k

=1,…,

d

)需要

Time

=

O

(1)，計算

x

()(

t

)(

i

=1,…,

n

;

k

=1,…,

d

)同步后的更新值

x

()(

t

+1)需要

Time

=

O

(

n

)。所以步6到步8需要

O

(

dn

)的時間代價。步9需要

O

(

dn

)的時間代價。步10到步14只需要

O

(1)的時間代價。步16只需要

O

(1)的時間代價。步17需要

O

(

dnK

)的時間代價，其中

K

是聚類數和孤立點數之和，一般有

K

?

n

。根據上面的分析，算法2的時間代價為

Time

=

O

(

Tdn

)。

2.4 參數的優化確定

算法1和算法2中的迭代退出閾值參數

ε

僅影響著同步迭代的次數及聚類精度，一般可設置在[0.01,0.000 001]范圍內。在所有實驗中，均設置為

ε

=0.000 01。算法1的近鄰閾值參數

δ

可以影響數據集的聚類結果。參數

δ

的優化設置原則是：如果兩個數據點的相異性度量小于

δ

，那么可以認為這兩個點應該在同一個聚類中。在文獻[8]中，參數

δ

可以通過MDL原理來優化確定。根據文獻[16]中的定理1和性質1，很容易選擇確定參數

δ

的一個合適值。驗中的參數

δ

就是根據這個方法確定的。通過大量的仿真實驗發現，在多數具有明顯聚類結構的數據集中，參數

δ

都具有一個比較寬泛的有效值范圍。在文獻[23]中，給出了如下兩種估計參數

δ

有效值的方法。(1)第一種估計參數

δ

有效值的方法由式(15)表示：

MstEdgeInCluster

≤

δ

<

DisDifferentClusters

。

(15)

式(15)中，

MstEdgeInCluster

是聚類簇的所有最小生成樹(每個聚類有一個將該聚類所有點連接在一起的最小生成樹)中的最大邊;

DisDifferentClusters

是不同聚類中的兩個點的最小相異性度量。(2)第二種估計參數

δ

有效值的方法是一個基于數據集

S

(或它的一個樣本)的最小生成樹而設計的一個算法。具體步驟如下：①首先從數據集

S

中構造出一個最小生成樹

MST

。②接著對該

MST

的所有邊進行升序排列。設排序后的邊集表示為

ES

(

MST

(

S

))={

e

,

e

,…,

e

-1},這里

e

≤

e

≤…≤

e

-1。③在

ES

(

MST

(

S

))中，搜索具有最大差值的兩個相鄰邊。這樣，估計參數

δ

有效值的另外一個公式可表示為：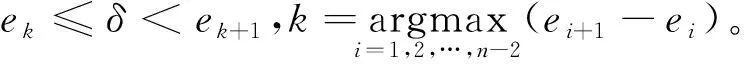

(16)

式(16)中，

e

和

e

+1是

ES

(

MST

(

S

))中具有最大差值的兩個相鄰邊。

3 仿真實驗

3.1 仿真實驗設計

表1 仿真實驗數據集的描述(a 4類2維實值型人工數據集的描述)

表1 仿真實驗數據集的描述(b 8個UCI數據集的描述[24])

相關實驗均在Intel(R)Celeron(R)CPU 3855U 1.6 GHz上進行，配備8 G內存，在Windows 7的Visual C++6.0開發環境下采用C語言和C++語言混合編程進行仿真實驗驗證。

為比較這些同步聚類模型的聚類結果和時間效率的差異，采用表1中描述的4類人工數據集和8個UCI數據集做一些仿真實驗。表1a給出了4類人工數據集的基本描述信息，它們是由兩個函數根據設定的參數在區域[0,600]×[0,600]內生成的2維數據。這兩個函數的C語言代碼在文獻[16]的附加材料附錄2中給出。表1b是8個UCI數據集的簡單描述。

這里采用多個不同類型的數據集對基于六種同步模型的聚類算法(分別基于定義2、定義3、定義4、定義5、定義6和定義7構造的同步聚類算法)在時間代價(單位為s)、同步迭代次數、聚類區域的穩定位置與均值位置的差異值和聚類質量(采用3個基于信息論的度量指標AMI/AVI/NMI)上進行適當的比較，觀察分析這六種同步聚類模型的聚類有效性差異。同步聚類算法中的迭代退出閾值參數ε均設置為0.000 01。在算法1中，基于定義2、定義3、定義4和定義7的同步聚類模型,根據文獻[16]的方法為近鄰閾值參數δ選擇一個合適值。

3.2 六種同步模型的動態聚類過程示例與比較

圖1采用的數據集選自表1a中的DS1類，數據點數目為400，具有5個比較明顯的聚類區域。在幾個同步聚類模型的算法中，參數

δ

設置為30，參數

ε

設置為0.000 01，最大迭代次數設置為50，定義3中的

v

(

t

)·

Δt

設置為0.1。圖1a～圖1e給出了六種同步聚類模型在這個數據集上的同步聚類過程演變軌跡，用NC(Number of Clusters)記錄著聚類數目，

t

記錄著迭代的輪次。

通過比較定義2、定義3、定義4、定義5、定義6和定義7可以看出，除了定義2是非線性的同步聚類模型，其他幾個定義都是線性的同步聚類模型。從圖1中可知，除了基于定義4的同步聚類模型外，其他幾個同步聚類模型都不能獲得良好的局部聚類效果。

3.3 人工數據集的仿真實驗結果

表2是基于六種同步模型的聚類算法在4個人工數據集(表1a中的4類人工數據集，數據點數目設置為1 000。第1個數據集具有5個比較明顯的聚類區域，無噪聲點；第2個數據集具有4個比較明顯的聚類區域，含3個噪聲點；第3個數據集具有6個比較明顯的聚類區域，無噪聲點；第4個數據集具有5個比較明顯的聚類區域，含15個噪聲點)上的實驗結果比較。在表2中，數據點數目n及算法所需設置的參數δ的具體值附在數據集后的括號內。表2的實驗不設置最大迭代次數，參數

ε

設置為0.000 01，定義3中的

v

(

t

)·

Δt

設置為0.1。3個指標AMI/AVI/NMI的取值基本上可以反映出聚類質量(采用人工觀察到的聚類區域或孤立點來設置基準聚類標號)的好壞。式(10)所表示的差異值指標反映出同步聚類后聚類區域的穩定點集與平均點集之間的平均差異。時間和迭代次數反映出聚類速度。

3.4 UCI數據集的仿真實驗結果

基于六種同步模型的聚類算法在8個UCI數據集上的實驗結果比較如表3所示。由表3可見，算法所需設置的參數

δ

的具體值附在數據集后的括號內。表3的實驗不設置最大迭代次數，參數

ε

設置為0.000 01，定義3中的

v

(

t

)·

Δt

設置為0.1。3個指標AMI/AVI/NMI的取值基本上可以反映出聚類純度(采用數據集本身的類別號來設置基準聚類標號)的好壞。式(10)所表示的差異值指標反映出同步聚類后聚類區域的穩定點集與平均點集之間的平均差異。時間和迭代次數反映出聚類速度。

圖1 基于定義2、定義3、定義4、定義5、定義6和定義7的同步聚類模型的動態聚類過程比較

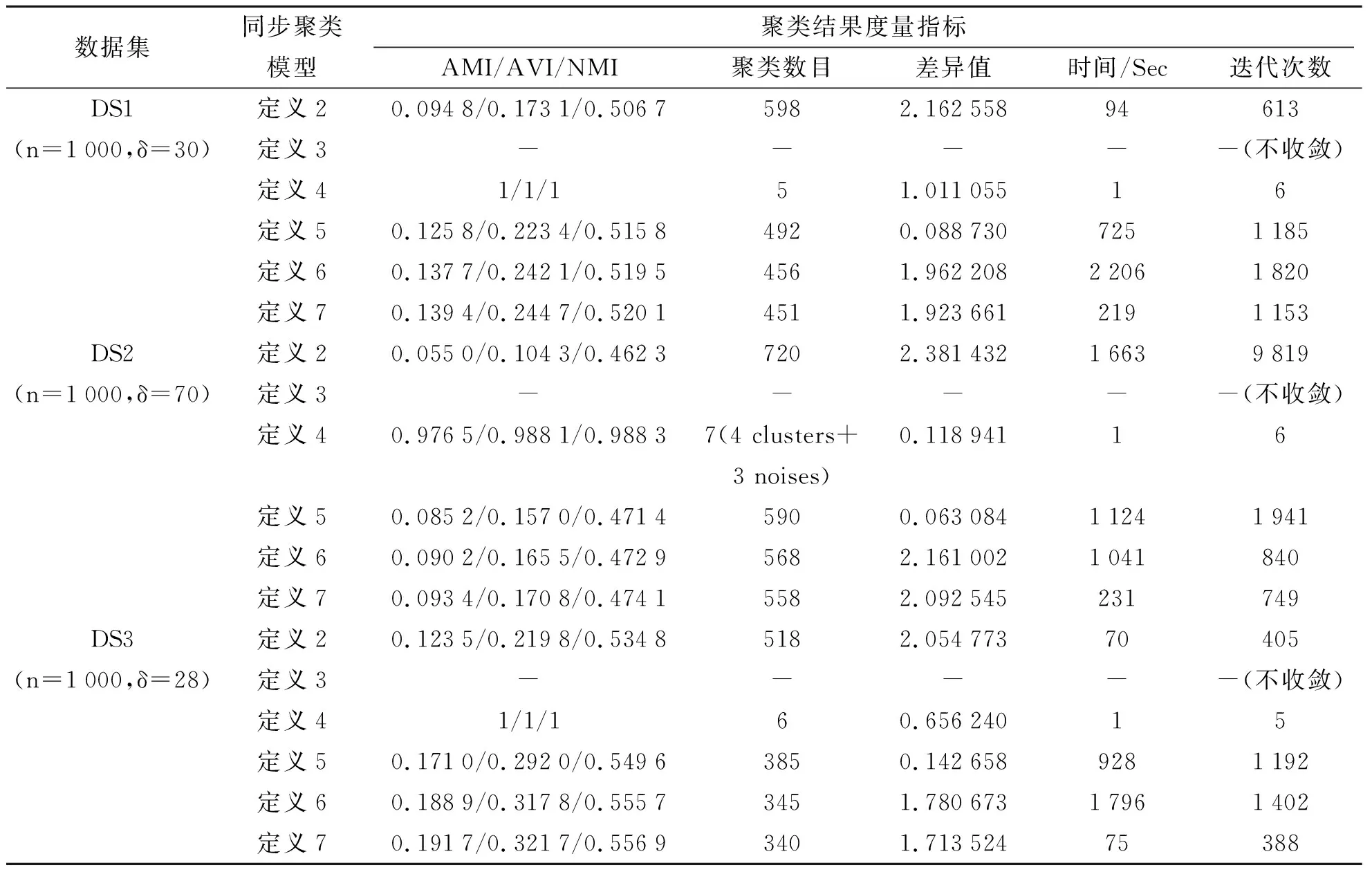
表2 人工數據集的實驗結果

續表2

3.5 實驗結果分析及結論

從圖1的實驗結果可以看出，基于定義4的同步聚類算法的聚類效果最好，其他幾種同步聚類模型雖然具有一定的同步效果，但它們的聚類結果不能很好地反映出數據集的聚類結構。從表2的實驗結果可以看出，基于定義4的同步聚類算法的聚類質量總體上最優，聚類速度最快。從表3的實驗結果可以看出，基于定義4的同步聚類算法的聚類質量總體上最優。通過比較表2和表3還可以看出，有的UCI數據集使用幾個同步聚類模型進行聚類時，或者運行時間過長，難以在有效時間范圍內達到迭代的終止條件，或者只經歷一次迭代就滿足迭代終止條件而退出循環。基于定義5的同步聚類算法的差異值指標通常都取得了最小值，但最終的聚類數目和AMI/AVI/NMI值并不理想，這是因為這個模型的同步幅度小，未獲得良好的聚類效果。基于定義2和定義3的同步聚類算法在多數情況下長時間都不能正常地迭代退出同步聚類過程，說明相鄰兩次迭代的均方誤差一直都較大，不能進入同步穩定階段。

基于定義4的同步聚類算法在迭代次數、聚類效果方面總體上表現最好。這種基于近鄰范圍內的均值位置更新式(即基于定義4)的迭代同步模型在聚類分析領域非常有效，其聚類效果遠優于基于定義2的同步聚類模型(即文獻[8]首次提出的擴展Kuramoto同步聚類模型)、基于定義3的同步聚類模型和研究提出的另外三種同步聚類模型(分別基于定義5、定義6和定義7)。研究提出的三種同步聚類模型雖然是基于萬有引力定律和指數衰減規律而提出來的，但在聚類上的應用效果總體上不如基于Vicsek模型的線性版本(即基于定義4)。

另外，我們還觀察到，AMI和AVI指標能較好地度量聚類質量，而NMI指標有時偏好于聚類結果中簇數目較多的情況。具體來說就是，當聚類結果與基準聚類不一致時，簇數目較多的聚類結果的NMI值遠遠大于簇數目較少的聚類結果。例如，Glass數據集有210個數據點，當把每個點當作一個單聚類(即孤立點)時，其NMI值為0.530 6，大于對應6個聚類和29個孤立點時的NMI值0.454 0。

表3 8個UCI數據集的實驗結果(a 前4個UCI數據集的實驗結果)

續表3a

表3 8個UCI數據集的實驗結果(b 后4個UCI數據集的實驗結果)

4 結束語

在聚類分析領域，常見的同步模型有擴展的Kuramoto模型，基于Vicsek模型的線性版本，基于第二個線性版本的Vicsek模型，萬有引力同步模型等。擴展的Kuramoto模型采用一種非線性的動態同步迭代公式來計算每一個迭代步驟的新位置，而基于Vicsek模型的線性版本采用一種線性的動態同步迭代公式來計算每一個迭代步驟的新位置，基于第二個線性版本的Vicsek模型采用一種加權的線性同步迭代公式來計算每一個迭代步驟的新位置。從研究及文獻[16]和文獻[25]的一些仿真實驗可以看出，后兩種同步模型更適合應用到聚類分析中。

KMeans和FCM(Fussy C-Means)等基于劃分的聚類算法速度快、應用廣，但需要事先設定正確的聚類數目，而且多適合于球狀類聚類結構的數據集。同步聚類算法具有在多個尺度、多個層次上探測出數據集的聚類結構，易于發現孤立點等優點。在Sync算法、ESynC算法和SSynC(Shrinking Synchronization Clustering)算法中，參數δ的有效取值范圍一般都比較寬泛。但沒有使用空間索引結構的同步聚類算法需要O(Tdn2)的時間復雜度。近年來流行的譜聚類算法是一種建立在譜圖理論上，將聚類問題轉化為圖的最優分割問題，可以在特征空間上進行聚類的方法。但譜聚類算法仍難以避免如下幾個缺點，如聚類結果的好壞依賴于數據集相似度矩陣的構造，聚類數目需要人工設定，最大特征向量集的選擇影響著最終的聚類結果，需要

O

(

n

)的時間和空間復雜度等。

下一步，我們將對譜聚類算法與同步聚類算法做一些比較分析研究，嘗試綜合它們的優點設計出更為優秀的聚類算法。還可以采用MapReduce框架來實現并行版本的MLSynC方法，并將該方法應用到位置數據的時空分析中。最后，從理論上證明這些同步聚類模型的迭代收斂性，并將ESynC算法應用到文本聚類和Web日志分析中也是未來可以嘗試的工作。