基于改進(jìn)B&B 算法的綜合能源系統(tǒng)優(yōu)化調(diào)度研究
李天博,段成俊,陳坤華
(江蘇大學(xué)電氣信息工程學(xué)院,江蘇鎮(zhèn)江 212013)
0 引言
能源是人類社會(huì)和經(jīng)濟(jì)發(fā)展的保障性資源,面對(duì)日益加劇的能源危機(jī)以及能源大規(guī)模使用帶來(lái)的環(huán)境污染和全球氣候變暖等一系列問(wèn)題,世界各國(guó)對(duì)能源發(fā)展給予了極大重視[1-3]。綜合能源系統(tǒng)(Integrated Energy System,IES)作為人類社會(huì)能源的主要承載形式,由社會(huì)供能網(wǎng)絡(luò)和終端綜合能源單元系統(tǒng)(也稱微網(wǎng))構(gòu)成,將電力、燃?xì)狻⒐?供冷等能源環(huán)節(jié)與交通、信息等支撐系統(tǒng)有機(jī)融合[4-6]。通過(guò)該系統(tǒng)可實(shí)現(xiàn)多種能源間的生產(chǎn)、轉(zhuǎn)換、消費(fèi)等多環(huán)節(jié)協(xié)調(diào)優(yōu)化,從而降低用能成本,提高能源利用率[7]。
瑞士蘇黎世聯(lián)邦理工學(xué)院(ETH Zurich)在能源網(wǎng)絡(luò)項(xiàng)目研究中提出能源集線器(Energy Hub,EH)模型可實(shí)現(xiàn)綜合能源系統(tǒng)中多能源間的耦合[8];文獻(xiàn)[9-13]基于能源集線器模型,針對(duì)電—?dú)狻獰崮茉淳W(wǎng)絡(luò)構(gòu)成的IES 進(jìn)行潮流計(jì)算、協(xié)調(diào)優(yōu)化調(diào)度及能量管理等問(wèn)題研究;文獻(xiàn)[14]和[15]針對(duì)太陽(yáng)能—生物質(zhì)能—儲(chǔ)能綜合能源系統(tǒng)進(jìn)行節(jié)能和成本效益分析,并驗(yàn)證系統(tǒng)可靠性與經(jīng)濟(jì)性;文獻(xiàn)[16]和[17]對(duì)同時(shí)包含光儲(chǔ)系統(tǒng)的區(qū)域能源系統(tǒng)進(jìn)行物理和數(shù)學(xué)模型構(gòu)建,并以運(yùn)行成本最低為目標(biāo)建立優(yōu)化模型,給出了相應(yīng)優(yōu)化調(diào)度策略。
能源優(yōu)化調(diào)度問(wèn)題多數(shù)為混合整數(shù)非線性規(guī)劃(Mixed-integer Nonlinear Programming,MINLP)模型,包括大量離散變量、連續(xù)變量和非線性函數(shù)[18]。近年來(lái),國(guó)內(nèi)外學(xué)者主要采用近似算法和精確算法,初步解決了一些MINLP 模型實(shí)際求解問(wèn)題[19]。近似算法主要是啟發(fā)式算法,如智能算法,求解速度快,但是不能保證求得全局最優(yōu)解[20-21]。文獻(xiàn)[22]采用人工蜂群算法,可有效解決非凸模型的調(diào)度問(wèn)題,但其本身屬于隨機(jī)搜索,存在參數(shù)選取困難,計(jì)算結(jié)果不一致等缺點(diǎn);文獻(xiàn)[23]和[24]采用改進(jìn)粒子群算法,實(shí)驗(yàn)表明,該算法針對(duì)MINLP 問(wèn)題具有求解速度快的優(yōu)點(diǎn),但容易陷入局部最優(yōu)。目前針對(duì)MINLP 模型的精確算法主要是分支定界(Branch and bound,B&B)算法,但存在搜索能力不足的缺點(diǎn)[25]。
因此,本文提出一種改進(jìn)的B&B 算法求解能源優(yōu)化調(diào)度問(wèn)題。改進(jìn)的B&B 算法通過(guò)采用兩個(gè)分離變量增強(qiáng)原算法利用能力的同時(shí),也可以提高搜索解效率。通過(guò)綜合能源系統(tǒng)MINLP 模型構(gòu)建,將改進(jìn)算法用于典型的能源優(yōu)化調(diào)度,并與原算法進(jìn)行比較,驗(yàn)證改進(jìn)算法優(yōu)越性。
1 多能互補(bǔ)的綜合能源系統(tǒng)穩(wěn)態(tài)模型
本文綜合能源系統(tǒng)主要由傳統(tǒng)電力系統(tǒng)、太陽(yáng)能光伏光熱系統(tǒng)、沼氣系統(tǒng)和能源集線器組成。
1.1 傳統(tǒng)電力系統(tǒng)模型
在不同總線上注入的有功功率與無(wú)功功率如式(1)、式(2)所示。
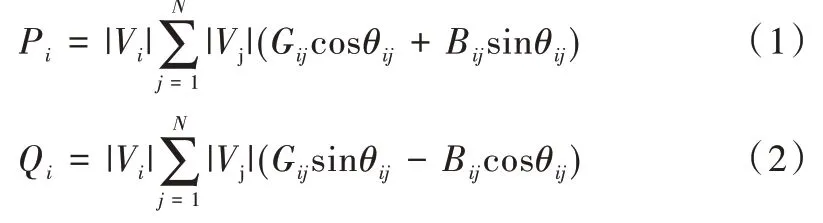
其中,Pi為節(jié)點(diǎn)i注入的有功功率,Qi為節(jié)點(diǎn)i注入的無(wú)功功率,Vi、Vj分別為節(jié)點(diǎn)i、節(jié)點(diǎn)j的電壓,Gij、Bij分別為節(jié)點(diǎn)i、節(jié)點(diǎn)j之間的電導(dǎo)和電納。
1.2 太陽(yáng)能光伏光熱系統(tǒng)模型
1.2.1 太陽(yáng)能光伏電池出力模型
太陽(yáng)能光伏電池板輸出功率很大程度上取決于光照條件和環(huán)境溫度。因此,太陽(yáng)能光伏電池板實(shí)際輸出功率可由標(biāo)準(zhǔn)額定條件下的額定輸出功率、光照強(qiáng)度和環(huán)境溫度得到,輸出功率可由式(3)表示。
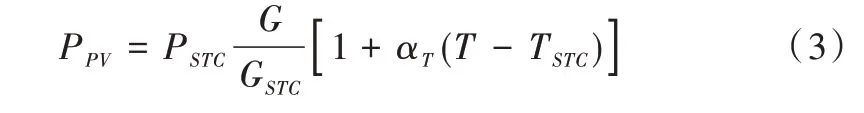
其中,PPV為光伏電池輸出功率,GSTC為太陽(yáng)光照強(qiáng)度,TSTC為光伏電池表面溫度,設(shè)為25℃,G為實(shí)際光照強(qiáng)度,PSTC為標(biāo)準(zhǔn)額定條件下光伏電池板額定輸出功率,αT為溫度特征系數(shù),T為光伏電池板表面實(shí)際溫度。
1.2.2 太陽(yáng)能集熱器出力模型
太陽(yáng)能集熱器輸出功率類似于光伏電池板,取決于光照強(qiáng)度和集熱面積大小。集熱器輸出熱功率如式(4)所示。
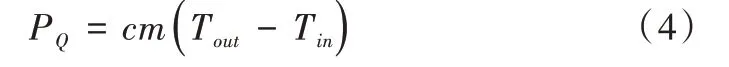
其中,c為水的比熱容,m為集熱管中水的質(zhì)量流量,Tout和Tin分別為集熱管中水出口溫度和入口溫度。
1.3 沼氣系統(tǒng)出力模型
沼氣輸出量依賴于消化池內(nèi)溫度,采用多項(xiàng)式回歸擬合測(cè)量數(shù)據(jù),得出沼氣出力模型,如式(5)所示。
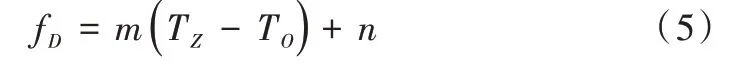
其中,Tz和TO分別為消化池的實(shí)際溫度和最佳溫度,m和n是從數(shù)據(jù)擬合中得到的系數(shù)。
1.4 能源集線器構(gòu)建
本文提出的電—太陽(yáng)能—沼氣能源組合在能源集線器的作用下,實(shí)現(xiàn)多能源間生產(chǎn)、轉(zhuǎn)換和分配。能源集線器組成如圖1 所示。
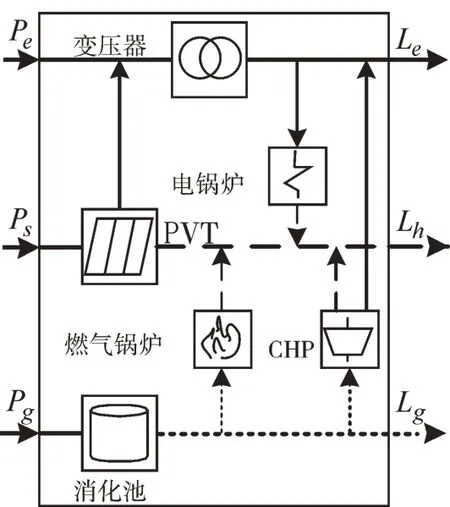
Fig.1 Energy hub圖1 能源集線器
能源集線器由變壓器、電鍋爐、PVT 裝置、燃?xì)忮仩t、CHP 和消化池組成。由外部電網(wǎng)提供的電力在變壓器的作用下一部分供給日常電負(fù)荷,另一部分在電鍋爐作用下給熱負(fù)荷提供能量;太陽(yáng)能通過(guò)PVT 裝置產(chǎn)生的電能在逆變器的作用下傳送到輸電線路,集熱器產(chǎn)生的熱能通過(guò)水循環(huán)實(shí)現(xiàn)生活用水、家庭供暖等目的;消化池內(nèi)產(chǎn)生的沼氣通過(guò)CHP 發(fā)電,其發(fā)電余熱滿足部分熱負(fù)荷,熱負(fù)荷由燃?xì)忮仩t保障。其能源集線器耦合矩陣如式(6)所示。
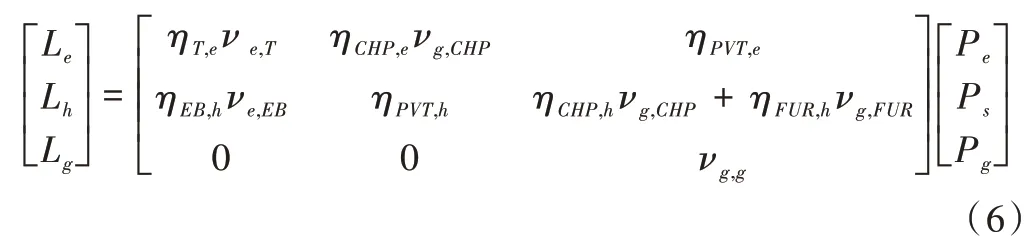
其中,ve,T和ve,EB是電能調(diào)度因子,vg,CHP,vg,FUR和vg,g為沼氣調(diào)度因子;ηT,e為變壓器效率,ηCHP,e和ηCHP,h為CHP 產(chǎn)生電能和熱能效率,ηPVT,e和ηPVT,h為PVT 產(chǎn)生電能和熱能效率,ηFUR,h為燃?xì)忮仩t產(chǎn)熱效率。
2 綜合能源系統(tǒng)MINLP 模型
2.1 模型目標(biāo)函數(shù)
根據(jù)電力-太陽(yáng)能-沼氣系統(tǒng)本身的特點(diǎn),以日為研究周期合理選擇安排能源集線器各裝置的啟停,使在各周期內(nèi)總運(yùn)行成本最少。本文提出基于場(chǎng)景滾動(dòng)視野策略的隨機(jī)優(yōu)化方式,每個(gè)滾動(dòng)步驟考慮沼氣池和PVT 出力的不確定性以及將來(lái)光照強(qiáng)度和環(huán)境溫度。構(gòu)建的目標(biāo)函數(shù)如式(7)所示。
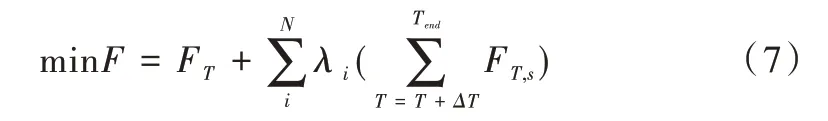
其中,F(xiàn)T為當(dāng)前時(shí)間段總運(yùn)行成本,包括購(gòu)電成本、設(shè)備維護(hù)成本和轉(zhuǎn)換單元啟停費(fèi)用;N為總場(chǎng)景數(shù);λi為場(chǎng)景i的概率;FT,s為在時(shí)間間隙T的運(yùn)行成本;Tend代表協(xié)調(diào)優(yōu)化結(jié)束。
購(gòu)電成本如式(8)所示。

其中,ζt和Pt分別為時(shí)間段t的購(gòu)電價(jià)格和購(gòu)電功率;T為單位時(shí)間長(zhǎng)度。
設(shè)備維護(hù)成本如式(9)所示。
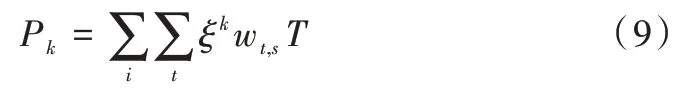
其中,ζk為設(shè)備i輸出單位功率維護(hù)成本;wt,s為能量轉(zhuǎn)換單元i在時(shí)刻t的輸出功率。
CHP 單元啟停費(fèi)用如式(10)所示。
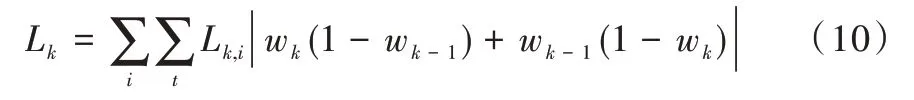
其中,Lk,i為設(shè)備i單位時(shí)間的啟停成本;wk是二進(jìn)制變量1 和0,表示轉(zhuǎn)換單元啟停狀態(tài)。
2.2 模型約束條件
2.2.1 電力網(wǎng)絡(luò)約束
變壓器約束如式(11)所示。
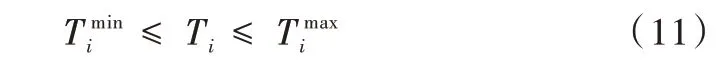
其中,和分別為變壓器在i條支路變比的下限和上限。
安全約束如式所示。
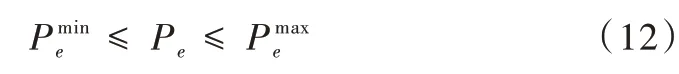
其中,和分別為線路中電功率的下限和上限。
電鍋爐約束如式(13)所示。

其中,為電鍋爐的最大輸出值。
2.2.2 太陽(yáng)能光伏光熱系統(tǒng)約束
熱水管道約束如式(14)所示。

其中,w和v分別為集熱器管道末端和首端出口溫度。
2.2.3 沼氣系統(tǒng)約束
CHP 約束如式(15)、(16)所示。
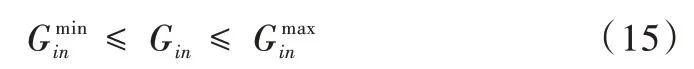
其中,和分別為CHP 沼氣輸入率下界和上界。

其中,CCHP為CHP 熱電比率;ФCHP為CHP 產(chǎn)熱量;PCHP為CHP 產(chǎn)電量。
燃?xì)忮仩t約束如式(17)所示。

其中,TF,max為燃?xì)忮仩t允許最大輸出。
沼氣管網(wǎng)約束如式(18)所示。

其中,m和n分別為沼氣管道首端和末端壓力。
3 基于MINLP 模型的優(yōu)化
MINLP 模型全局最優(yōu)解的求解核心是分支定界算法,但其存在搜索能力不足的缺點(diǎn)。因此本文提出一種改進(jìn)的B&B 算法解決MINLP 模型求解問(wèn)題。
3.1 改進(jìn)的B&B 算法
傳統(tǒng)B&B 算法在分離過(guò)程中只使用一個(gè)變量xk構(gòu)造兩個(gè)子問(wèn)題。如果要解決兩個(gè)結(jié)果的子問(wèn)題,傳統(tǒng)B&B 算法需遍歷A 和B 兩個(gè)區(qū)域搜尋解,在搜尋過(guò)程中可能會(huì)對(duì)已檢查過(guò)的空間再次掃描,降低分離過(guò)程的搜索效率。因此,本文對(duì)傳統(tǒng)B&B 算法作兩點(diǎn)改進(jìn)。
(1)采用兩個(gè)分離變量。本文提出同時(shí)選擇xk和xj作為分離變量,采用該方式一方面可避免對(duì)區(qū)域A∩B、A∩C、A∩D、B∩C、B∩D、C∩D 不必要的掃描,從而可以提高搜索解效率,如圖2 所示;另一方面,建立的劃分區(qū)域不僅可掃描非凸搜索空間,而且也有減少子問(wèn)題數(shù)量的可能性。
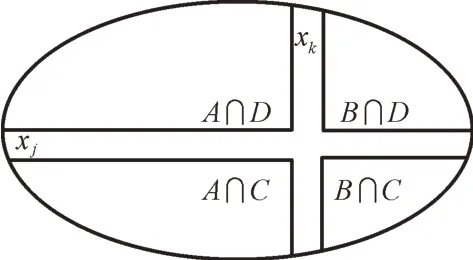
Fig.2 Searching method圖2 搜索方式
為更有效選擇分離變量,本文對(duì)搜索解采用如式(19)、(20)所示的定義,其中M 和m 用于計(jì)算變量,進(jìn)一步減小目標(biāo)函數(shù)值。
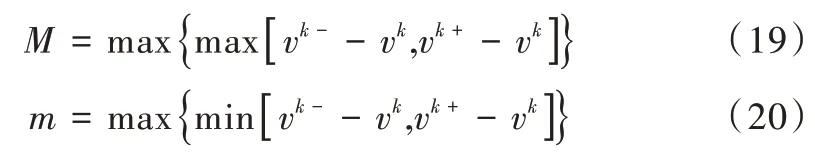
(2)選擇有效的子問(wèn)題。傳統(tǒng)B&B 算法在選擇要分離的變量并建立新的子問(wèn)題后沒(méi)有考慮到哪個(gè)子問(wèn)題優(yōu)先級(jí)更高。為了更好地選擇待解決的子問(wèn)題,本文采用如下策略:①設(shè)定搜索寬度(B),并始終選擇搜索解的最小值作為決策變量選擇下一個(gè)要分析的子問(wèn)題;②針對(duì)在解決完給定子問(wèn)題的NLP 問(wèn)題后,NLP 問(wèn)題沒(méi)有收斂。本文提出的算法將再次為求解器提供起始點(diǎn)。如果再次出現(xiàn)NLP問(wèn)題不收斂,將再次要求求解器從上次出現(xiàn)不收斂的點(diǎn)處解決NLP 問(wèn)題。如果經(jīng)歷3 次嘗試之后,NLP 問(wèn)題依然沒(méi)有收斂,此時(shí)可認(rèn)為NLP 問(wèn)題不能收斂,同時(shí)刪除各自節(jié)點(diǎn)。此外,對(duì)于不可行的NLP 問(wèn)題,本文提出對(duì)目標(biāo)函數(shù)使用一組變量和懲罰因子,通過(guò)重置虛擬變量的策略解決算法對(duì)于問(wèn)題的不適應(yīng)性。
3.2 B&B 算法改進(jìn)
綜上所述,改進(jìn)后的B&B 算法步驟如下:
(1)初始化。取k=0 并設(shè)置初始解和初始待解決的子問(wèn)題,然后存儲(chǔ)相應(yīng)NLP 解的組件。
(2)檢查收斂性。如果待解決子問(wèn)題的列表為空,則當(dāng)前解即為最優(yōu)解;否則,進(jìn)行下一步。
(3)選擇要檢查的待選子問(wèn)題。選擇一個(gè)未在待解決列表中探究的子問(wèn)題,并使用最小vk作為決勝局選擇下一個(gè)子問(wèn)題,同時(shí)解決相應(yīng)的NLP 和存儲(chǔ)最優(yōu)解。
(4)測(cè)驗(yàn)。待解決的子問(wèn)題會(huì)因滿足下列其中一個(gè)條件被刪除:①某個(gè)子問(wèn)題不可行;②當(dāng)算法找到原MINLP問(wèn)題的1 個(gè)解,此時(shí)測(cè)驗(yàn)③。更新vk,如有必要,進(jìn)入待解決子問(wèn)題列表中檢查③,假設(shè)所有子問(wèn)題均已探究,返回第(2)步;③如果某個(gè)子問(wèn)題的解滿足vk>vk+ε。
(5)選擇變量分離的數(shù)量。在整數(shù)變量中,如果實(shí)際值不是整數(shù),而且有多個(gè)變量,這時(shí)選擇其中兩個(gè)變量進(jìn)行分離并生成4 個(gè)子問(wèn)題。設(shè)置k=k+4,返回第(3)步。假設(shè)只有一個(gè)可分離的變量,設(shè)置k=k+2,同樣返回第(3)步。
4 實(shí)例分析
以某區(qū)域作為研究對(duì)象,其中配電網(wǎng)額定電壓為35kV,地下管式沼氣消化池容積為500m3,PVT 裝置、電鍋爐、CHP 單元、燃?xì)忮仩t裝機(jī)容量分別為20kW、50kW、100kW 和100kW。另外,該綜合能源系統(tǒng)耦合設(shè)備關(guān)鍵參數(shù)如表1 所示。
以1 天24 小時(shí)為運(yùn)行周期,協(xié)調(diào)調(diào)度周期定為15min,在每個(gè)時(shí)間周期,預(yù)測(cè)的環(huán)境溫度可以用非線性回歸方法從歷史數(shù)據(jù)中獲得。該區(qū)域典型日電、氣、熱負(fù)荷曲線如圖3 所示。

Table 1 Key parameters of coupling equipment表1 耦合設(shè)備關(guān)鍵參數(shù)
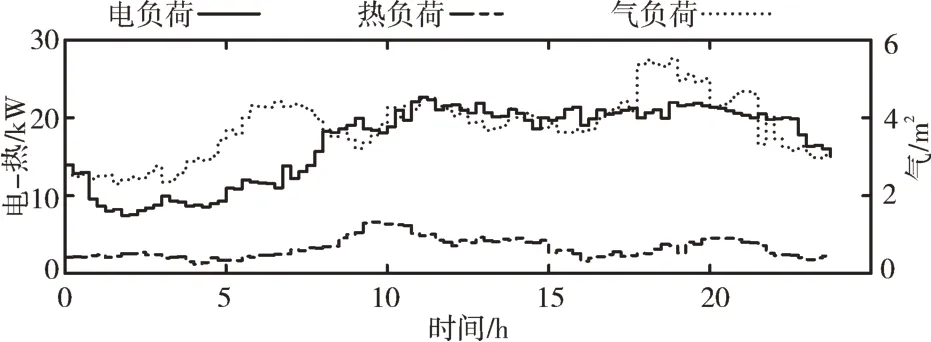
Fig.3 Load curve圖3 負(fù)荷曲線
4.1 各耦合設(shè)備出力
為分析模型和算法性能,本文使用改進(jìn)的算法對(duì)B&B樹(shù)每個(gè)節(jié)點(diǎn)出現(xiàn)的非線性規(guī)劃問(wèn)題進(jìn)行求解。綜合能源系統(tǒng)各耦合設(shè)備出力如圖4、圖5 和圖6 所示。
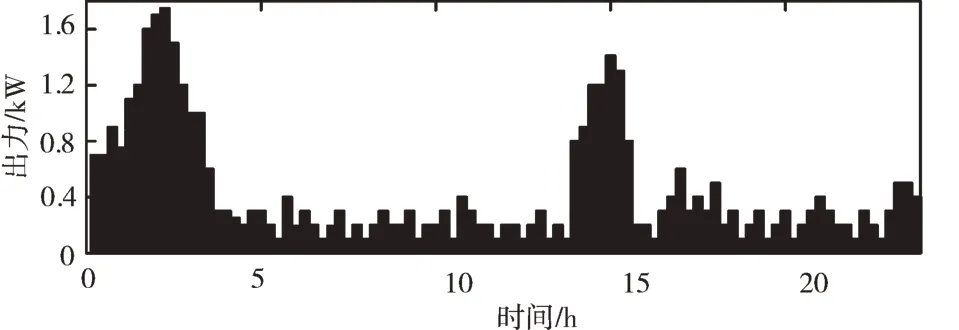
Fig.4 Daily energy output of electric boiler圖4 電鍋爐日能量輸出
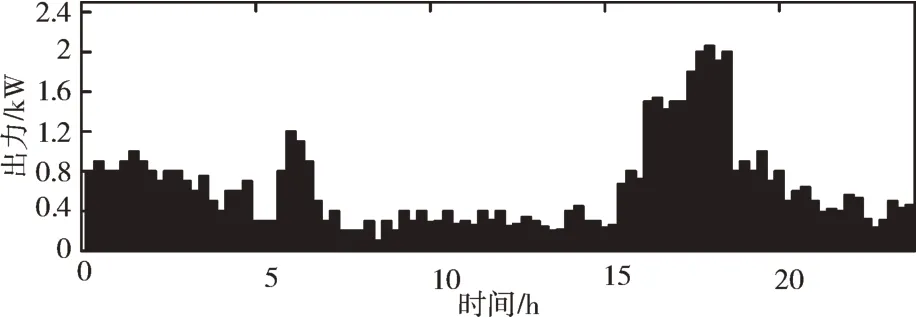
Fig.5 Daily energy output of gas fired boiler圖5 燃?xì)忮仩t日能量輸出
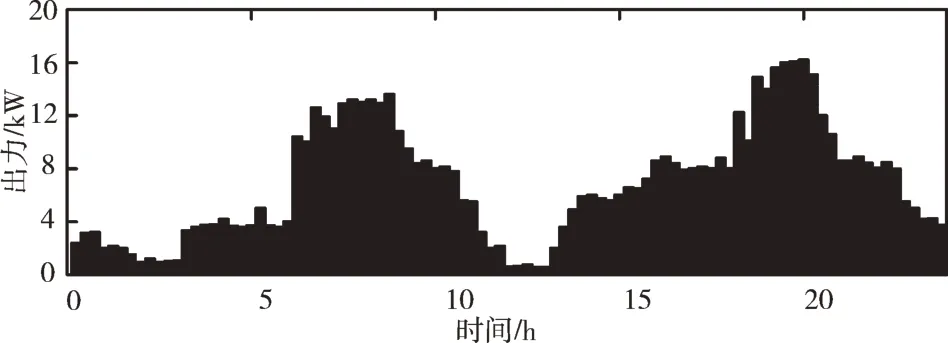
Fig.6 CHP daily power output圖6 CHP 日電力輸出
由圖4 可知,考慮到該區(qū)域環(huán)境溫度較高,為降低需求側(cè)用能成本,電鍋爐輸出能量較少,且能量輸出規(guī)律與居民生活習(xí)慣密切相關(guān)。由圖5 可知,由于沼氣池中的厭氧生物在高溫環(huán)境中活性強(qiáng),因而沼氣產(chǎn)率隨之提升,這種現(xiàn)象在日照較強(qiáng)的14:00-16:00 時(shí)段尤為明顯。由圖6可以看出,一方面CHP 出力明顯,用戶側(cè)熱負(fù)荷多數(shù)為CHP承擔(dān);另一方面CHP 出力隨負(fù)荷而顯著變化,如在夏季18:00-20:00 時(shí)段里,CHP 通過(guò)增大輸出量滿足飆升的負(fù)荷。
4.2 優(yōu)化調(diào)度結(jié)果
圖7 和圖8 分別表示典型日下各個(gè)時(shí)段電功率和沼氣流量?jī)?yōu)化調(diào)度結(jié)果。
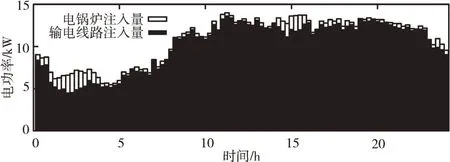
Fig.7 Electric power injection圖7 電功率注入量
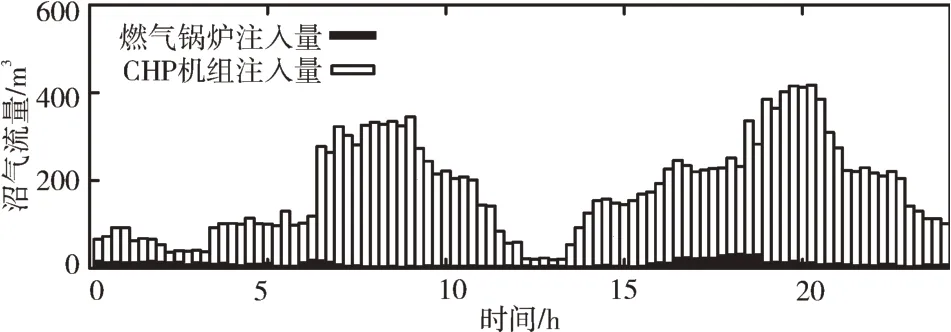
Fig.8 Biogas consumption圖8 沼氣消耗量
4.3 算法對(duì)比分析
為體現(xiàn)本文改進(jìn)的B&B 算法在尋最優(yōu)解的速度性與各個(gè)周期內(nèi)運(yùn)行成本的經(jīng)濟(jì)性,與文獻(xiàn)[20]所用的傳統(tǒng)B&B 算法進(jìn)行對(duì)比。本文MINLP 模型采用改進(jìn)的B&B算法得出計(jì)算結(jié)果,如圖9 所示。
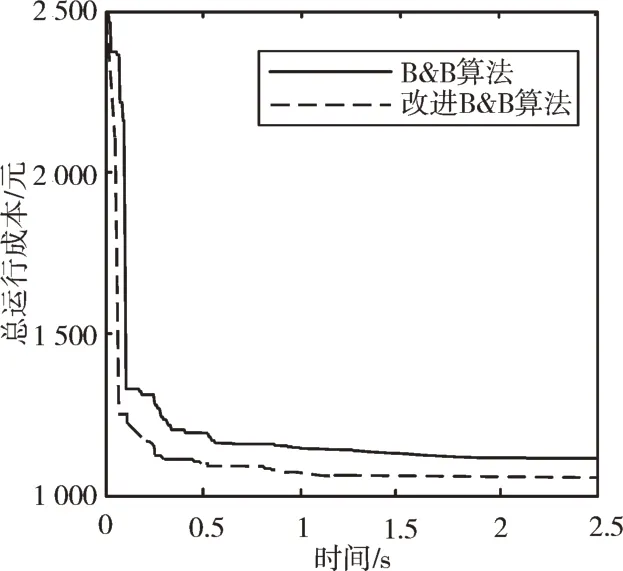
Fig.9 Comparison curve of calculation results圖9 計(jì)算結(jié)果對(duì)比曲線
為更直觀、有效地分析改進(jìn)的B&B 算法求解綜合能源系統(tǒng)優(yōu)化調(diào)度中的快速性和收斂性,比較計(jì)算結(jié)果,如表2所示。
由表2 可知,在同等負(fù)荷條件下,本文方法可降低各周期內(nèi)的運(yùn)行成本,且搜索最優(yōu)解的速度也較文獻(xiàn)[20]的方法更快,具有良好的參考價(jià)值。

Table 2 Comparison of calculation results表2 計(jì)算結(jié)果對(duì)比
5 結(jié)語(yǔ)
將B&B 算法作為MINLP 模型全局最優(yōu)解的求解核心存在搜索能力不足的問(wèn)題,因此本文提出一種改進(jìn)B&B 算法以求解綜合能源系統(tǒng)多能流協(xié)同調(diào)度問(wèn)題。改進(jìn)算法通過(guò)采用兩個(gè)分離變量增強(qiáng)原算法利用能力的同時(shí),也提高了搜索解效率。本文以各周期內(nèi)運(yùn)行成本為目標(biāo)函數(shù),將改進(jìn)B&B 算法用于多能互補(bǔ)的綜合能源系統(tǒng)MINLP 模型計(jì)算,并與傳統(tǒng)算法進(jìn)行比較,驗(yàn)證算法優(yōu)越性。
其次,改進(jìn)B&B 算法可根據(jù)實(shí)際情況選擇優(yōu)先級(jí)更高的子問(wèn)題,以更好地選擇待解決的子問(wèn)題,進(jìn)而增強(qiáng)算法利用能力。
最后,本文在解決綜合能源系統(tǒng)日間經(jīng)濟(jì)調(diào)度時(shí),重點(diǎn)考慮了主要耦合設(shè)備及管網(wǎng)存在的約束條件,部分裝置可能存在多限制運(yùn)行區(qū),這是相當(dāng)復(fù)雜的非線性約束,也是下一步研究?jī)?nèi)容。

