基于IGM-BP算法的城軌越區切換研究

魏 偉，劉曉娟，張雁鵬，李 瑤

(1.蘭州交通大學電子與信息工程學院，蘭州 730070；2.蘭州交通大學自動化與電氣工程學院，蘭州 730070)

引言

隨著通信、計算機、自動控制等“3C”技術的發展與進步，城市軌道交通中通信、信號等技術也得到了提高和完善。目前，國內一些新建的城市軌道交通線路也采用了可靠性較高的TD-LTE(Time Division Long Term Evolution，分時長期演進)技術承載城市軌道交通車地通信業務。北京地鐵燕房線是首次采用TD-LTE技術進行列控系統綜合承載傳輸，更是第一條采用了國內自主化FAO系統UTO(Unattended train operation，無人值守下的列車自動運行)模式的線路[1]。TD-LTE技術具有傳輸速率高、移動性好、系統時延低以及多級QoS(Quality of Service，服務質量)完善等優勢[2]，為列車更加安全可靠地運行提供了保障的前提，代表著未來軌道交通技術的發展方向。

基于TD-LTE的城市軌道交通環境下，列車往往會因為受到多徑效應、同頻干擾等因素的影響引起接收到的RSRP值的波動較大的問題[3]，進而導致乒乓切換頻繁發生。由于TD-LTE技術切換時采用的是硬切換，所以乒乓切換次數較多會降低切換成功率，影響列車通信性能。

國內外一些學者也對越區切換問題做了大量研究。文獻[4]提出了一種基于錨的多連接架構，給定用戶與多個AP連接，選擇最佳接入點作為切換錨點，提供控制平面，從而降低切換概率；文獻[5]提出了一種利用列車定位技術進行切換的機制，不通過場強觸發切換，而是通過列車到達某一特定位置后觸發切換條件，減少了切換時延；文獻[6]綜合考慮了RSRP(Reference Signal Receiving Power，參考信號接收功率)和RSRQ(Reference Signal Received Quality，參考信號接收質量)兩種測量值，利用灰色預測GM(1，N)模型預測下一時刻兩個相鄰基站場強值，保證了切換過程的QoS(Quality of Service，服務質量)；文獻[7]利用Stackelberg博弈模型，提出一種協作分集技術的列車切換算法，與傳統切換算法相比，提高了網絡資源分配效率，同時也減少了切換時延。

針對越區切換頻繁的問題，本文提出了一種IGM-BP神經網絡算法，并采用MATLAB作為仿真工具，對該算法和傳統算法以及灰色預測算法進行仿真比較，驗證本文提出的算法的可行性和有效性。相比現有的算法和研究，本文提出的算法能進一步減少乒乓切換的頻率，提高了切換成功率。

1 基于TD-LTE的越區切換概述

TD-LTE技術作為未來城市軌道交通發展的趨勢，使列車在高速移動下具有較高傳輸穩定性，同時，采用基于IP的扁平化網絡結構，降低了系統時延[8]。因而，采用TD-LTE技術是實現城市軌道交通車地雙向通信更加安全可靠的不可或缺的一環[9]。

1.1 TD-LTE車地通信系統

TD-LTE技術不僅能滿足城市軌道交通綜合業務承載需求[10]，而且可以保障城市軌道交通列車在切換過程中安全可靠運行。TD-LTE車地通信系統結構如圖1所示。

圖1 TD-LTE車地通信系統結構

TD-LTE車地通信系統結構主要由核心網子系統、無線子系統eNB及終端設備等各子系統組成。其中核心網子系統采用A網、B網冗余雙網設計，兩張網絡完全獨立，互不影響；無線子系統eNB包括BBU(Based Band Unit，基帶處理單元)和RRU(Remote Radio Unit，射頻拉遠單元)設備，其中，單個BBU下可以連接多個RRU，實現無線通信系統信號的全線鏈狀覆蓋，同時TAU(Terminal Access Unit，車載數據終端)也可以與軌旁RRU實現數據傳輸。

1.2 切換流程

列車越區切換過程主要分為切換測量、切換判決和切換執行[11]，其切換流程及主要功能如表1所示。

表1 切換流程及主要功能

在切換判決階段，3GPP LTE協議標準中規定了A1，A2，A3，A4，A5，B1，B2等7種測量報告觸發事件[13]，其中，系統內越區切換測量事件主要包括A1～A5事件，另外兩種事件主要用于系統外的切換測量觸發事件。A3事件常作為城市軌道交通中切換觸發測量報告事件，其判決公式如下

Mn+Ofn+Ocn-Hys>Mp+Ofp+Ocp+Off

(1)

式中，在不考慮任何偏置的情況下，Mn和Mp分別代表接收到的目標小區及服務小區的RSRP值；Ofn和Ofp分別為目標小區、服務小區的特定頻率偏置；Ocn和Ocp分別為目標小區、服務小區的特定偏置；Hys為A3事件的遲滯參數；Off為A3事件的偏置參數。由于同頻組網方式是LTE系統使用較多的組網方式，所以Ofn和Ofp相同，不參加計算，且相鄰小區配置均相同，則Ocn與Ocp也不參加計算。因此，式(1)可化簡為式(2)

Mn-Hys>Mp

(2)

A3事件切換觸發示意如圖2所示，當目標小區RSRP值Mn與服務小區RSRP值Mp的差值大于切換遲滯門限Hys且滿足觸發時延TTT后才會觸發切換。

圖2 A3事件切換觸發示意

2 基于IGM-BP的越區切換算法

根據城市軌道交通的特點，在灰色預測算法和BP神經網絡算法的基礎上進行組合預測，故將本文算法記為IGM-BP算法。

2.1 灰色預測算法及模型建立

灰色系統理論1982年由鄧聚龍首先提出創立，它是一種不確定性系統，主要針對的是樣本數量少且信息一部分已知，一部分未知的系統。GM(1，1)模型則是其中一種最基礎也是應用最廣泛的模型，它是一種離散時間響應函數近似呈指數規律的模型[14]，使用4個數據便可以開始建立模型進行預測。GM(1，1)模型的核心思想是先將原始數據進行處理，找到一定的規律后開始建立模型，擬合數據值，得到預測值。其建模步驟如下。

(1)設X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))

為一組非負原始數據序列，將序列X(0)進行一階累加生成運算，得累加生成序列為

X(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))

(3)

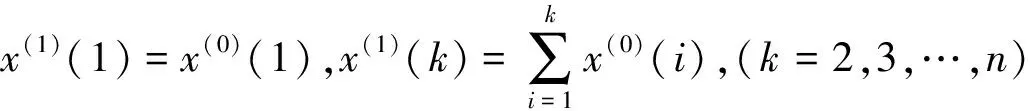
(2)根據第一步得到的累加序列X(1)建立GM(1，1)模型，得對應的白化微分方程為

(4)

式中，a為發展系數；b為灰色發展作用量。對應的灰微分方程形式為

x(0)(k)+αz(1)(k)=b，k=2，3，…，n

(5)

(3)求參數a，b。通過最小二乘法計算參數列Φ=[a，b]T，展開式為

Φ=(BTB)-1BTY

(6)

其中，

k=2，3，…，n

(7)

(8)

將k=2，3，…，n代入上式，便可得到初始數據的擬合值；當k>n時，便可得到灰色模型對未來的預測值，同時對預測值取均值。

2.2 BP神經網絡及結構設計

20世紀80年代中期，Rumelhart和McClelland等提出了BP神經網絡(Back Propagation Neural Network)結構，它是按照誤差逆向傳播算法訓練的多層前饋神經網絡[15]，現被廣泛應用于各個領域。

BP神經網絡結構分為3層，即輸入層、隱層和輸出層，任意一層都可以有若干個節點，每一層間的節點都相互聯系。由于本文目的是對RSRP的波動情況進行改善，所以BP神經網絡結構設計如下。

(1)輸入層：因為本文針對RSRP值進行優化，所以輸入層的維度為1。輸入值為經灰色預測算法后得到的預測值，記為X=[x1，x2，…，xn]，其中，n為該層神經元節點數，本實驗取節點數為5。

(2)隱層：首先考慮單隱層的BP神經網絡，即只有一個隱層。一般來說，當維度為1時，如果網絡性能在節點數較多的情況下還是不能得到改善，才會增加隱層的維度。本文選擇1個隱層即可滿足網絡性能，且實時性較好，符合城市軌道交通實時的要求。對于傳遞函數來說，本文采用(0，1)S型函數中f(x)=1/(1+e-x)作為傳遞函數。

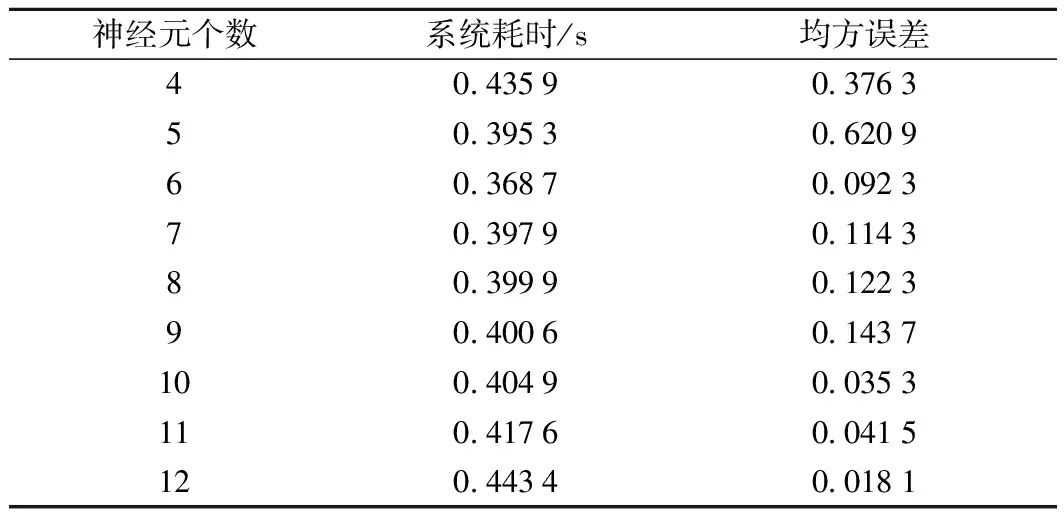
表2 不同隱層神經元個數性能比較

(3)輸出層：該層維度也為1，即經過算法得到的該時刻的RSRP預測值。

2.3 IGM-BP算法

在城市軌道交通中，進行服務小區和目標小區的場強測量周期為50 ms，列車周期上報的時間是240 ms[17]，因此在這一過程中，對服務小區和目標小區的RSRP值最多進行4次測量。為了使灰色GM(1，1)模型更適合城市軌道交通的特點，本文先取4個RSPR數據建立灰色預測模型進行預測。

由于灰色預測的精確度與初始值相關，對于離原點數據較遠的點，隨著時間推移將會出現新的隨機因素，使得預測值發生較大偏差[18]，本文將對初始數據進行優化。在建立GM(1，1)的過程中，將IGM-BP算法得到的預測值x(0)(n+1)增加到X(0)序列中，并將X(0)中的x(0)(1)信息刪除，利用新序列X(0)'=(x(0)(2)，x(0)(3)，…x(0)(n+1))建立GM(1，1)模型，重復上述步驟直到預測結束。

本文將選取灰色預測得到的均值作為其BP神經網絡中的期望值，一方面是因為均值計算方便，可以很大程度上減小算法復雜度，另一方面是因為均值與預測得到的所有數據都有密切關系，可以改善數值變動較大造成預測結果的規律性減弱的負面影響，其算法流程如圖3所示。

圖3 算法流程

處理步驟如下。

(1)由于源數據Mn和Mp的值均為負數，則需要將所有源數據取絕對值。

(2)取t時刻接收到的服務小區的RSRP值的前4次值，并與上一時刻得到的預測值構成GM(1，1)模型短序列，記為X1={X1(t-4Δt)，X1(t-3Δt)，X1(t-2Δt)，X1(t-Δt)}，同理，記目標小區RSRP值構成的短序列為

X2={X2(t-4Δt)，X2(t-3Δt)，X2(t-2Δt)，X2(t-Δt)}；

(3)根據短序列X1建立GM(1，1)模型，進行運算后得出一組新的預測序列Y1={Y1，1，Y1，2，Y1，3，Y1，4，Y1，5}；同理，根據短序列X2建立GM(1，1)模型，進行運算后得出一組新的預測序列Y2={Y2，1，Y2，2，Y2，3，Y2，4，Y2，5}。

(9)

灰色預測算法一定程度上弱化了數據隨機性，可以很容易找出原始數據所呈現的規律性，具有建模樣本少、短期預測精度高等優點[18]。但是灰色預測模型也具有一定的固有的局限性，它十分依賴原始數據，如果原始數據的波動性較大，會出現較大誤差，則預測精度會大打折扣。

BP神經網絡有著良好的自適應性，學習能力較強，容錯性較高，可以進行并行計算，提高運算速度，使運算系統簡單，靈活[19]，在遇見波動性較大的數據時也可以進行較為精確的預測。但是需要較多的樣本數據進行學習，如果數據數量太少，得到的預測值也會出現較大的誤差。

當二者進行組合時，則可以互相發揮優勢，取長補短。由于RSRP波動性較大，該組合算法利用BP神經網絡修正灰色預測得到的數據誤差，可以改善灰色預測算法對數據波動較敏感的問題，比單一使用灰色預測算法的計算精度高；同時，該算法在數據量較少的情況下，其精度也比單一使用BP神經網絡算法得到的精度要高。

3 實驗仿真

將采用MATLAB軟件作為算法仿真平臺，通過傳統切換算法、灰色預測算法與本文提出的算法進行仿真對比，并從RSRP值的波動情況、乒乓切換率及切換成功率等方面來驗證3種算法對切換性能的影響。

3.1 實驗參數設置

以北京燕房線為例，燕房線全長14.431 km，全線為高架段[20]，同時使用頻率為1.8 GHz的無線信道，因此采用選擇1.5～2 GHz頻率范圍的COST231-HATA模型模擬城區無線環境[21]，在仿真中，僅考慮無線信道模型中的陰影衰落與路徑損耗，則服務小區和目標小區RSRP的計算公式分別為

RSRPi(d)=Pt-PLi(d)-Si(d)

(10)

RSRPj(d)=Pt-PLj(d)-Sj(d)

(11)

式中，Pt為基站發射功率；Si(d)和Sj(d)為兩個小區的陰影衰落；PLi(d)、PLj(d)分別為服務小區和目標小區的COST231-HATA模型路徑損耗功率，具體公式如下

PL(d)=46.3+33.9lgfc-13.82lghte+

(44.9-6.55lghte)lgd-α(hre)+Ccell

(12)

其中，fc為載波頻率；hte為基站天線發射高度；d為收發天線之間的水平距離；hre為移動臺天線高度，本文具體實驗參數如表3所示。

表3 實驗仿真參數

根據城市軌道交通的特點，小區呈鏈狀分布，因此將列車越區切換過程模擬如圖4所示。

圖4 鏈狀小區列車切換過程模型

AB段表示兩個基站間的距離為1.4 km；BD段表示兩個基站之間的切換重疊帶，C點為切換帶中點，切換帶規劃公式如下

x=Hys/L+2(t1+t2)·v

(13)

式中，x為單邊切換距離；Hys為遲滯切換參數；L為漏纜每米損耗；t1為測量時長；t2為切換時延；v為列車速度。一般來說，測量時長和切換時延在500 ms之內，由于北京燕房線列車最高運行速度為80 km/h，則單邊切換距離為94 m，那么重疊切換帶長度為188 m，取切換區域為0.6～0.8 km。

3.2 實驗結果分析

如圖5所示，圖中縱坐標代表的是使用傳統切換算法得到的目標小區和服務小區的RSRP值，橫坐標代表的是列車行駛過程中與初始服務小區基站間的距離。圖6和圖7分別代表的是灰色預測算法和采用本文所提出IGM-BP算法得到的目標小區和服務小區的RSRP值隨距離變化的情況。灰色預測算法相較于傳統A3算法，在一定程度上改善了RSRP值的波動情況，而對比于灰色預測算法，IGM-BP算法在改善RSRP值的波動情況方面又得到了優化，從圖中可以看出，本文所提出的算法在改善RSRP值的波動情況方面效果最好，波動幅度最小，說明本文算法有效減小了同頻干擾及多普勒效應等因素的影響。

圖5 傳統切換算法下RSRP值隨距離變化情況

圖6 灰色預測算法下RSRP值隨距離變化情況

圖7 IGM-BP算法下RSRP值隨距離變化情況

圖8分別給出了傳統切換算法(黑色點線)、灰色預測算法(藍色直線)和IGM-BP算法(黃色虛線)下目標小區與服務小區RSRP差值隨距離的變化情況，其中黑色虛線表示切換遲滯Hys。從圖8可以看出，在覆蓋重疊區域中RSRP差值在Hys處變化劇烈，尤其在切換帶中點0.7 km處附近變化幅度最大，容易產生乒乓切換，3種算法比較下得出傳統切換算法下目標小區與服務小區RSRP差值波動變化最大，灰色預測算法次之，IGM-BP算法下變化幅度最小，穩定性最高。在區域切換帶內取20 m為一步長，其3種算法下的RSRP差值如表4所示。

圖8 3種算法下目標小區與服務小區RSRP差值比較

表4 切換區域帶內三種算法RSRP差值比較

圖9為3種算法下的乒乓切換率比較，本文所提出算法的乒乓切換率最高只有3%，低于傳統算法和灰色預測算法的成功率21%和14%，從中可以得出，IGM-BP算法可有效減小乒乓切換的頻繁發生，提高了列車在FAO系統運行環境下的穩定性。

圖9 乒乓切換率比較

切換成功率是列車越區切換時重要的評估標準之一，由于本文改善了RSRP值的波動情況，越區切換成功率也得到了提高。3種算法下切換成功率比較如圖10所示，本文所提出的算法在0.76 km處的成功率達到99.6%，高于在此處的傳統算法和灰色預測算法成功率83.4%和92.7%。

圖10 三種算法切換成功率比較

4 結語

本文討論了基于TD-LTE的城市軌道交通越區切換問題，提出一種IGM-BP算法來改善列車行駛過程中接收到的服務小區和目標小區的RSRP值的波動情況。通過結合TD-LTE標準中的A3事件，對該算法進行實驗仿真，并且與既有算法和灰色預測兩種算法對比，仿真結果表明，該算法可以有效改善因為同頻干擾和多徑效應對RSRP值的干擾情況，減小了RSRP值的波動幅度，與其余兩種算法相比，IGM-BP算法降低了乒乓切換率，提高了切換成功率，具有明顯的優越性。