基于MATLAB的逐點比較法直線插補(bǔ)和圓弧插補(bǔ)算法的研究
陳 雨
(廣西大學(xué)行健文理學(xué)院,廣西 南寧 530000)
插補(bǔ)算法是數(shù)控機(jī)床計算機(jī)控制系統(tǒng)中重要的組成部分。逐點比較法是插補(bǔ)中使用最廣泛的算法之一,它既可以作直線插補(bǔ),又可以作圓弧插補(bǔ),其特點是運(yùn)算直觀,插補(bǔ)誤差小于一個脈沖當(dāng)量,輸出脈沖均勻,而且輸出脈沖的速度變化小,調(diào)節(jié)方便。因此,在兩坐標(biāo)聯(lián)動的數(shù)控機(jī)床中應(yīng)用較為廣泛[1]。本文分析了第一象限逐點比較法直線插補(bǔ)和圓弧插補(bǔ)的原理,分別給出計算公式和計算過程,最后基于MATLAB編程實現(xiàn),驗證結(jié)果。
1.第一象限內(nèi)逐點比較法直線插補(bǔ)
1.1 偏差計算公式
在第一象限想加工出直線段OA,直線段終點目標(biāo)A(xe,ye)已知,點m(xm,ym)為加工點,如圖1-1所示。
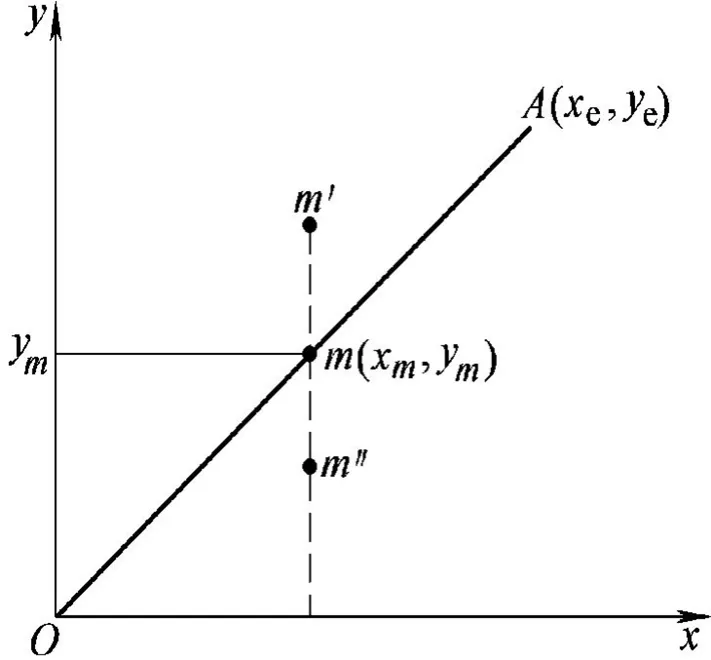
圖1-1 第一象限直線
圖中直線插補(bǔ)的偏差判別式為

第一象限逐點比較法直線插補(bǔ)的原理是:從直線的起點出發(fā),當(dāng)Fm≥0時,往+x軸的方向前進(jìn)一步;當(dāng)Fm<0,往+y軸的方向前進(jìn)一步;當(dāng)往+x和+y方向所經(jīng)的步數(shù)與規(guī)定的終點坐標(biāo)A(xe,ye)相同時,停止插補(bǔ)。
顯然式1-1的偏差計算做了兩次乘法,進(jìn)一步簡化偏差計算公式。當(dāng)Fm≥0時,往+x軸的方向前走一步,xm+1=xm+1,ym+1=ym,該點偏差為
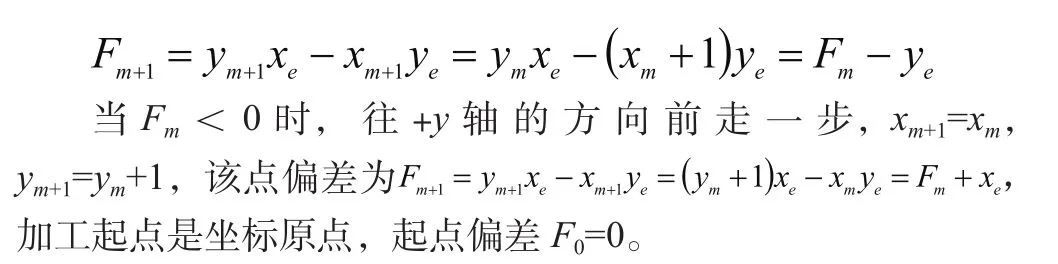
1.2 MATLAB程序?qū)崿F(xiàn)直線插補(bǔ)計算
直線插補(bǔ)的過程有四個步驟,分別是判別偏差、進(jìn)給坐標(biāo)、計算偏差和判斷終點。
取第一象限一條直線OA進(jìn)行加工,起點為原點o(0,0),終點為目標(biāo)A(4,5),步長初值為其中Xe=4,Ye=5,初始偏差值F0=0。
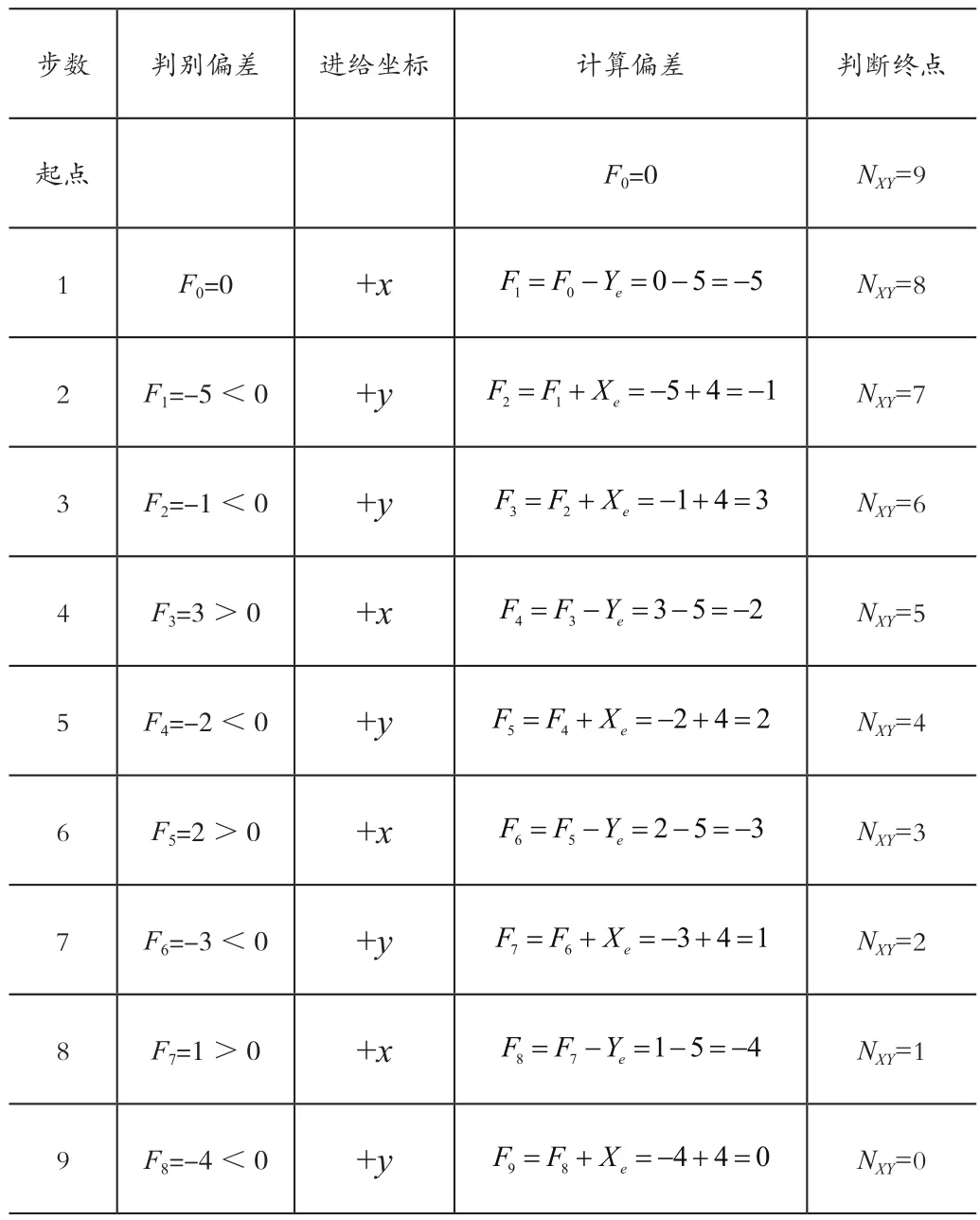
表1-1 計算直線插補(bǔ)
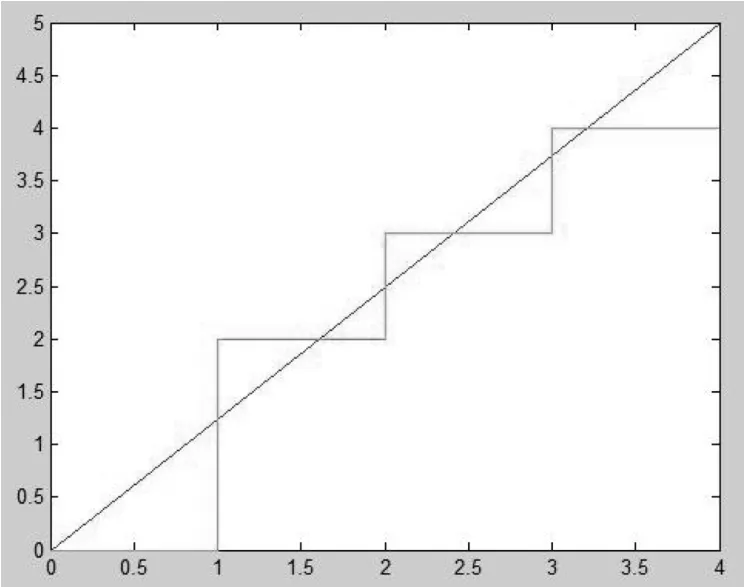
圖1-3 直線插補(bǔ)走步軌跡圖
2.第一象限內(nèi)逐點比較法圓弧插補(bǔ)
2.1 偏差計算公式
在第一象限加工逆圓弧AB,已知起點A(x0,y0),終點目標(biāo)B(xe,ye),圓弧半徑為R,點m(xm,ym)為加工點,如圖2-1所示。
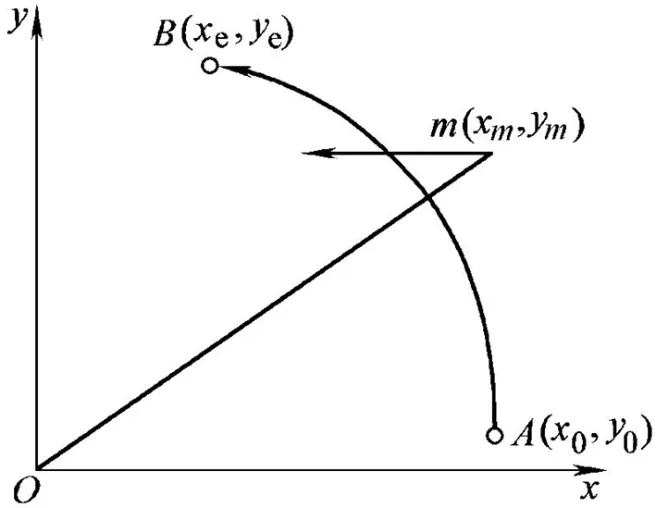
圖2-1 第一象限逆圓弧
圖中圓弧插補(bǔ)偏差判別式可以定義為

圖2-1中逆圓弧段逐點比較法插補(bǔ)原理為:從圓弧的起點A點出發(fā),當(dāng)Fm≥0時,往-x軸的方向前進(jìn)一步;當(dāng)Fm<0,往+y的方向前進(jìn)一步;當(dāng)往-x和+y方向所經(jīng)的步數(shù)與規(guī)定的終點坐標(biāo)B(xe,ye)相同時,停止插補(bǔ)。
式2-2偏差計算做了兩次乘法,進(jìn)一步簡化偏差計算公式。
當(dāng)Fm≥0時,往-x軸的方向前進(jìn)一步,xm+1=xm-1,ym+1=ym,新加工點偏差為
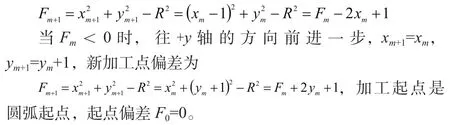
2.2 MATLAB程序?qū)崿F(xiàn)直線插補(bǔ)計算
圓弧插補(bǔ)的過程有五個步驟,分別是判別偏差、進(jìn)給坐標(biāo)、計算偏差、計算坐標(biāo)和判斷終點。
取第一象限一條逆圓弧AB,起點為點A(4,3),終點為B(5,0)。步長初值為
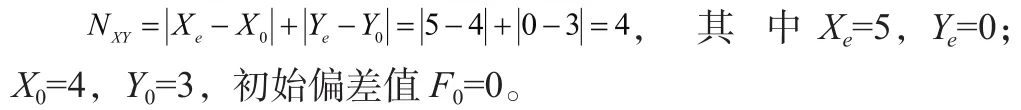
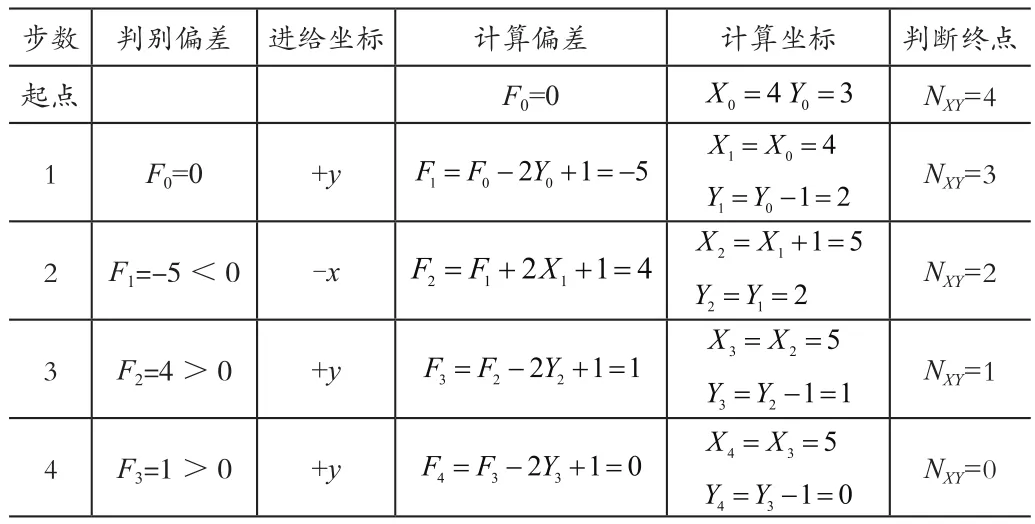
表2-1 計算圓弧插補(bǔ)

圖2-3 圓弧插補(bǔ)走步軌跡圖
3.結(jié)語
文中給出了逐點比較法第一象限直線插補(bǔ)和圓弧插補(bǔ)的詳細(xì)計算過程及MATLAB的程序?qū)崿F(xiàn)并仿真驗證。逐點比較法是用階梯式的折線來無限逼近直線或圓弧等曲線,這種方法與要加工的直線或圓弧的最大的誤差僅僅是一個脈沖當(dāng)量,所以把脈沖當(dāng)量值盡可能取足夠小,便可以達(dá)到加工精度要求。

