考慮空間電荷層效應的氧離子導體電解質內載流子傳輸特性*

徐晗 張璐

(西安交通大學建筑環境與能源應用工程系， 西安 710049)

1 引 言

氧離子導體作為一種關鍵電解質材料， 廣泛應用于化學傳感器、氧泵、燃料電池等能量轉換與儲存器件[1，2].例如固體氧化物燃料電池(solid oxide fuel cell， SOFC)常將ZrO2基(ZrO2-M2O3)， CeO2基(CeO2-M2O3)等螢石結構氧化物陶瓷作為電解質材料.氧離子導體內部存在多種界面， 包括同相材料晶粒與晶粒之間形成的晶界(grain boundary，GB)、不同相材料接觸形成的異質界面等[3].已有研究表明， 上述界面附近區域載流子傳輸特性顯著區別于體相區域， 表現出差異極大的導電性能， 例如， GB 電導率比體相低幾個數量級[4]， 薄膜電解質內異質界面電導率可比體相高幾個數量級[5].尤其涉及近些年得到廣泛關注的納米導體材料時， 界面的體積占比明顯提高， 導致其對導體內載流子傳輸的影響顯著增加， 而通過調控界面來提升材料電化學性能與穩定性也成為了當前相關領域的前沿研究熱點之一[6，7].

早期研究指出晶粒間存在雜質相會阻礙離子傳輸， 影響導體導電性能， 例如ZrO2基氧離子導體中存在具有高電阻率的SiO2是GB 區域電導率降低的原因[8].然而后續研究發現即使去除雜質相，GB 電導率仍然很低[9]， 由此指出該現象理應是GB的固有特性， 而空間電荷層(space charge layer，SCL)效應是產生這種現象的根源[10]: 導體中帶電點缺陷(例如氧離子導體中的氧空位)被分離到GB， 使得GB 帶有正電荷， 同時在GB 附近的體相形成帶負電的空間電荷層， 以保持整個導體電中性.帶電點缺陷的重新分布可能會使GB 附近局部點缺陷濃度產生高達幾個數量級的變化， 導致GB區域的導電性更強或者電阻更大.同時也有研究表明空間電荷層效應也是異質界面改善材料性能的重要因素之一[11，12]， 例如SOFC 納米復合電極及薄膜電解質等的發展就是得益于上述異質界面效應[13].因此， 考慮界面與體相之間的空間電荷層對局部載流子濃度與電勢的影響， 闡明導體內的載流子傳輸機理， 對理解相關物理現象、發展界面調控技術極為重要.

目前多采用Poisson-Boltzmann (PB)模型描述導體中SCL 效應[14-17].該模型采用Poisson 方程描述電勢分布， 基于Boltzmann 假設刻畫SCL內的載流子濃度分布.據此， 已有文獻發展了兩種簡化模型[15]: 1) Gouy-Chapman (GC)模型， 考慮陽離子受體和氧空位都可移動; 2) Mott-Schottky(MS)模型， 假設陽離子受體濃度在整個導體內不變， 僅氧空位移動.有學者基于上述研究， 忽略SCL內被消耗的載流子對電荷密度的貢獻或者假設SCL 內電勢線性分布， 獲得了基于GC 模型和MS模型的SCL 內電勢分布解析解.也有學者采用數值方法求解PB 模型， 并比較了GC 模型與MS 模型等的預測結果與數值求解結果的差異[18].然而，上述模型假設載流子在整個導體區域內處于電化學平衡狀態， 據此推導出載流子濃度在SCL 呈現Boltzmann 分布， 因此無需求解載流子質量守恒方程[19]， 但是該假設并不適用于載流子電化學勢梯度不為零的情況.然而， 在燃料電池等能量轉換器件中， 氧離子導體內載流子均具有電化學勢梯度驅動的宏觀運動， 因此需要耦合Poisson 方程和載流子質量守恒方程構建工況適用范圍更廣的數學模型.由于Poisson 方程具有關于載流子濃度的巨大源項(可達1015數量級)， 與質量守恒方程耦合數值求解的困難大， 因此即使導體內載流子具有明顯的宏觀運動， 現有文獻大多仍采用PB 模型進行SCL 效應分析[20].另外， 現有研究多基于有量綱參數分析SCL 內載流子傳輸特性， 而引入無量綱分析不僅能夠減少求解變量參數以簡化求解過程， 更有助于深刻理解物理問題本質[21，22].

鑒于上述研究現狀， 本文針對GB 或者異質界面附近的離子導體區域， 建立Poisson 方程與載流子質量守恒方程結合的耦合數學模型; 借助無量綱分析方法， 推導控制傳輸過程的關鍵無量綱參數，深入研究考慮空間電荷層效應的氧離子導體內載流子傳輸機理.

2 數學模型

如圖1 所示， 計算區域包括SCL 區域與體相(bulk)區域.左邊界(x = 0)為不同晶粒間的晶界核或兩相材料組成的異質界面(后文統稱為界面)，考慮真實物理過程(例如SOFC 復合電極中異質界面處載流子宏觀運動導致的電流)， 左邊界給定電流密度; 右邊界(x = x0)位于體相區域， 載流子濃度為體相濃度cbulk(可由導體體相電中性假設獲取)， 取該處電勢為參考電勢φref.由于本文主要關注垂直于界面方向的載流子傳輸特性， 該問題可簡化為沿x 方向的一維載流子擴散-遷移問題.

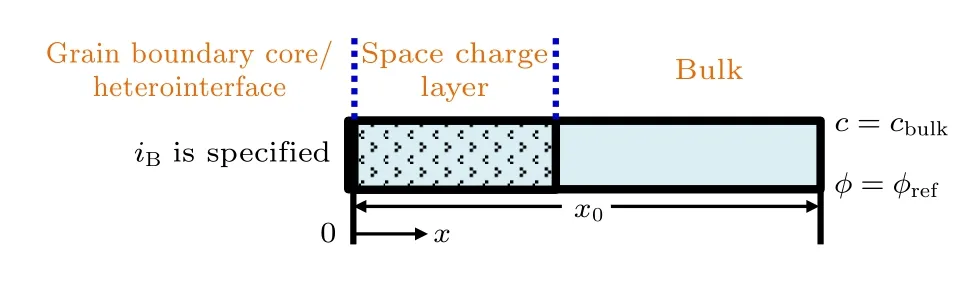
圖1 本文計算區域與邊界條件， 其中計算區域包括空間電荷層與體相區域Fig.1.Computational domain including the space charge layer and bulk area， and boundary conditions used in the present study.

2.1 Poisson-Boltzmann 方程

首先介紹廣泛應用于低摻雜濃度下離子導體空間電荷層內載流子傳輸特性模擬的PB 方程.該方程采用Poisson 方程描述電勢分布:

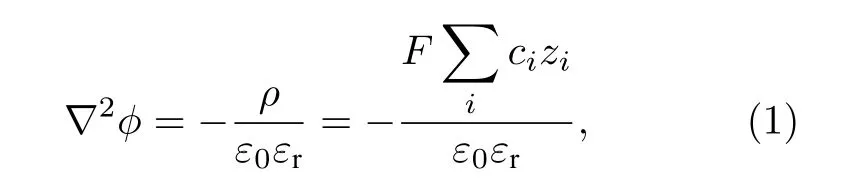
式中， φ 為電勢， ρ 為電荷密度， ε0與εr分別為真空與相對介電常數， z 為攜帶電荷數， F 為法拉第常數， c 為載流子濃度， 下標i 表示不同種類載流子.采用標準Maxwell-Boltzmann 方程描述載流子電化學勢:

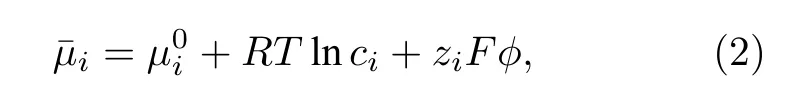
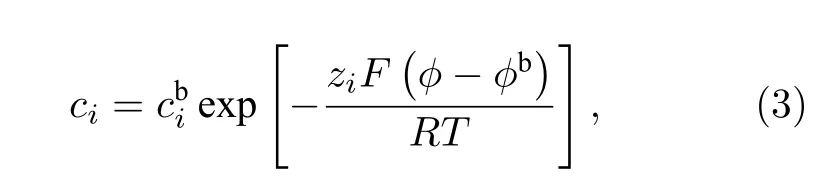
其中， 上標b 表示體相.(3)式也被稱之為Boltzmann 分布， 將(3)式代入(1)式， 即可得到如下PB方程:

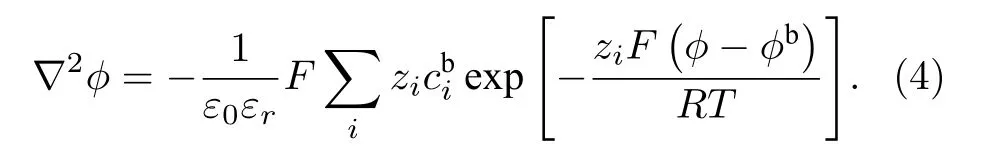
可見， PB 方程只求解電勢， 濃度是關于電勢的函數， 極大簡化了數值求解過程.

2.2 Poisson-載流子質量守恒耦合方程

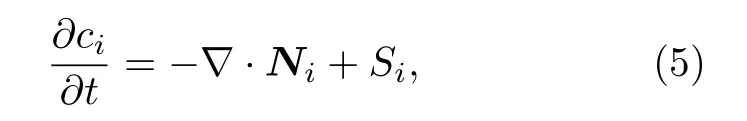
式中， S 為化學反應導致的源項(在本文中為零);N 為載流子摩爾通量密度， 可表示為

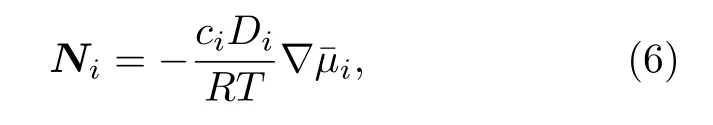
其中， D 為擴散系數.結合方程(5)和方程(6)， 可以得到載流子質量守恒控制方程為

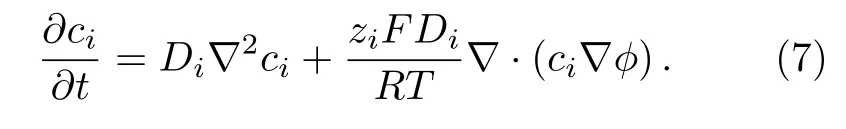
聯立方程(1)與方程(7)即可得到Poisson-載流子質量守恒耦合方程.載流子移動產生的電流密度可表示為

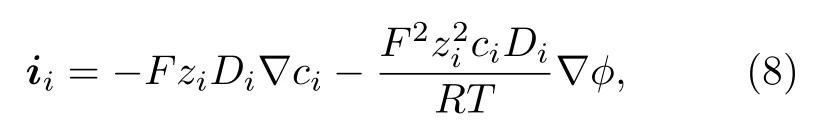
式中， 等號右邊第一項為濃度梯度導致的擴散電流密度idif， 第二項為電勢梯度導致的遷移電流密度imig.導體凈電流密度可表示為

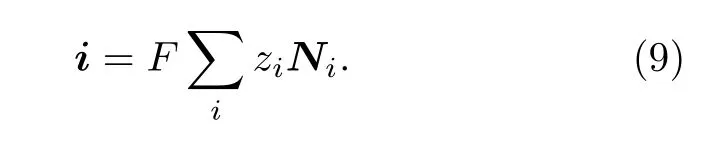
本文研究對象為M2O3摻雜的AO2氧化物，其缺陷反應方程式為

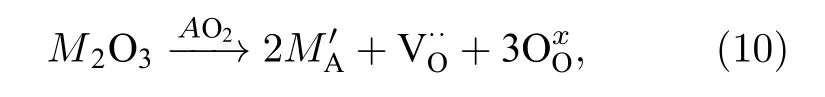
式中， M 與A 分別代表SOFC 電解質材料中常采用的Y 與Gd 等正三價金屬、Ce 與Zr 等正四價金屬，表示氧空位，表示晶格氧.摻雜M2O3后的AO2內部載流子包括陽離子受體與氧空位(分別用下標a 與V 表示)， 已有文獻指出陽離子受體僅在燒結溫度下才會移動[18]， 而本文主要關注運行工況下(溫度遠低于燒結溫度)離子導體內的載流子傳輸特性， 因此忽略陽離子受體濃度變化( ? ca=0 )， 只考慮氧空位移動.基于導體體相電中性假設可得:

SCL 電阻可采用下式計算[18]:

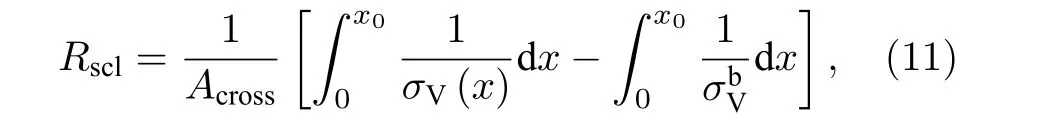
式中， Across為導體橫截面積， σV為電導率且σV=2cVDV/(RT).

2.3 無量綱分析

本文基于相同特征變量， 對PB 模型和Poisson-載流子質量守恒耦合模型均進行了無量綱化處理， 并給出了控制載流子傳輸過程的關鍵無量綱參數.選取導體長度x0、體相濃度cV0、界面處(x = 0)電流密度i0、時間步長t0分別為特征長度、特征濃度、特征電流密度以及特征時間， 取φ0=i0x0RT/()為特征電勢.可得以下無量綱PB 方程:

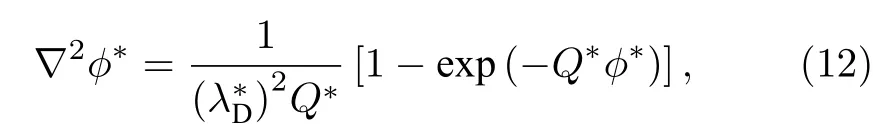
式中， 上標*表示無量綱數，為無量綱Debye 長度， Q*為無量綱電勢.

無量綱Poisson-載流子質量守恒耦合方程為

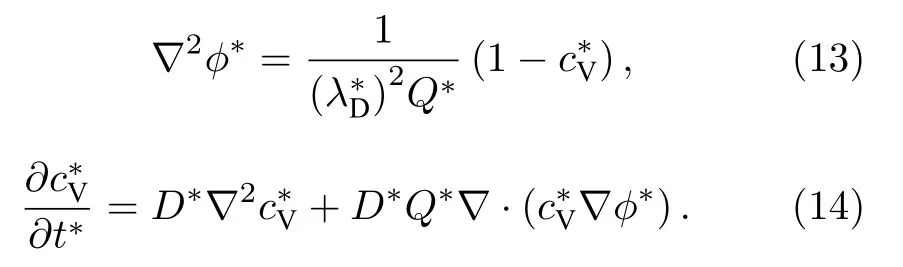
無量綱電流密度為

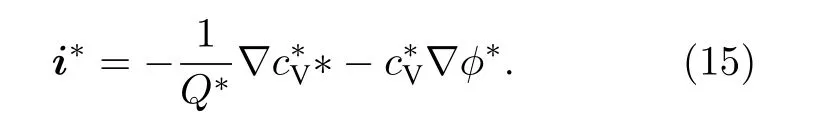
無量綱SCL 電阻為

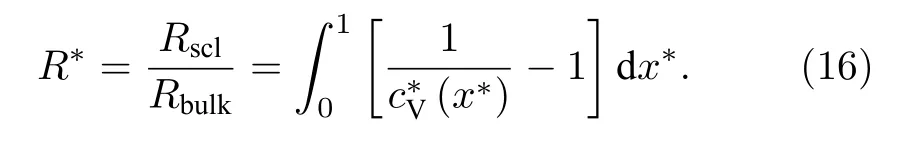
由于本文研究離子導體內載流子穩態傳輸特性， (14)式可進一步簡化為

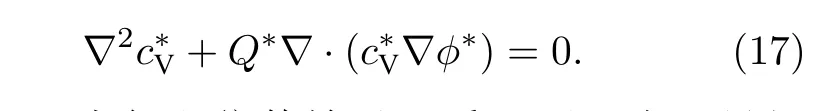
此時， SCL 內氧空位傳輸過程受以下兩個無量綱參數控制:

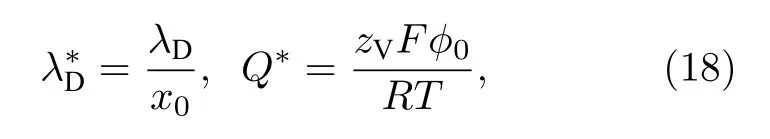
式中λD為Debye 長度， 可表示為

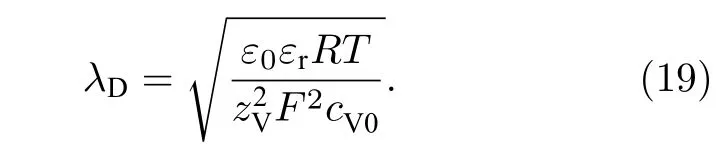
2.4 數值方法

已有研究表明格子Boltzmann (LB)方法可以很好地預測微通道內的電滲流過程[23，24]， 鑒于導體內載流子傳輸過程與電滲流過程遵循相似的控制方程， 本文采用LB 方法求解數學模型.(20)式為求解Poisson 和載流子質量守恒方程所采用的LB演化方程:

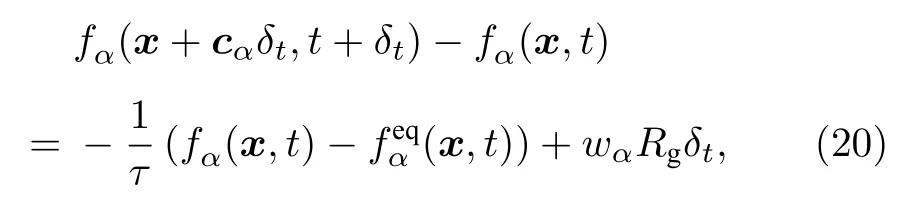
式中， fα為t 時刻位置x 處速度為cα的分布函數，δt為時間步長， wα為權函數， τ 為碰撞時間， Rg為原控制方程中的源項.為了后期便于將本文模型拓展到導體不規則異質界面， 采用二維LB 模型求解圖1 所示物理問題， 并對計算區域上下邊界采用周期性邊界條件.采用應用最為廣泛的D2Q9 模型描述演化方程(20)中的粒子遷移速度:

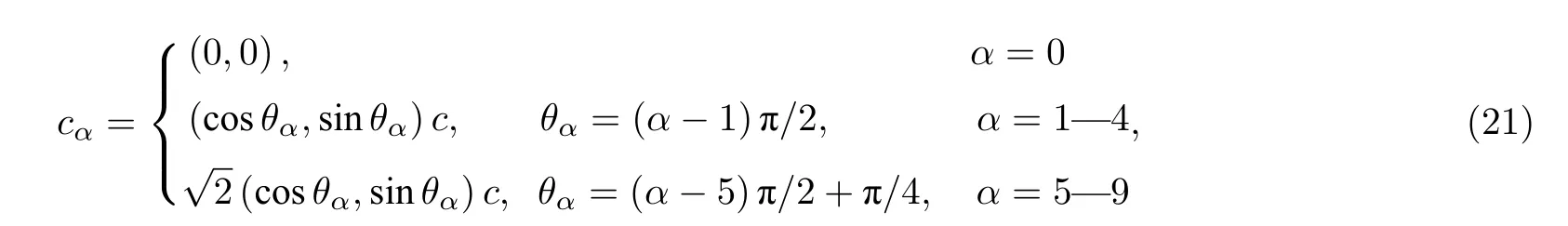
權函數wα可表示為

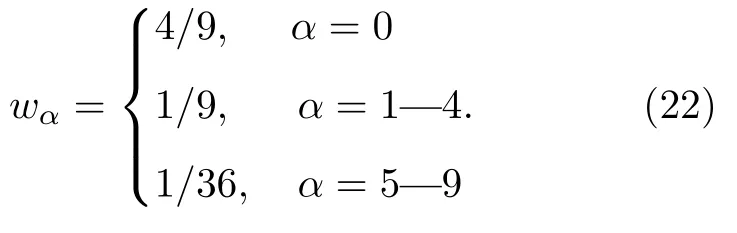
對演化方程(20)在不同的源項、平衡分布函數與求解變量表達式下(如表1 所列)進行Chapman-Enskog 多尺度展開， 在穩態下可分別還原為無量綱PB 方程、無量綱Poisson 方程與無量綱載流子質量守恒方程.本文僅以無量綱載流子質量守恒方程為例詳細描述Chapman-Enskog 展開技術還原控制方程過程.首先對(20)式中的時間、空間、分布函數及源項引入以下多尺度展開:

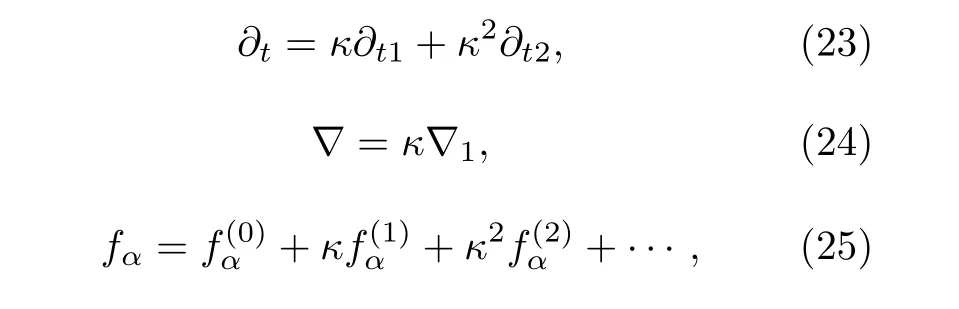
表1 演化方程(20)還原不同控制方程時所涉及的平衡分布函數、源項和求解變量表達式Table 1.Equilibrium distribution function， source term and variable expression in the evolution Eq.(20) for obtaining different governing equations.

式中， κ 為任意小量， t 1 與t 2 為連續時間尺度，Rg1為多尺度展開變量.將上述多尺度展開表達式代入(20)式， 并比較κ 的各階系數可得

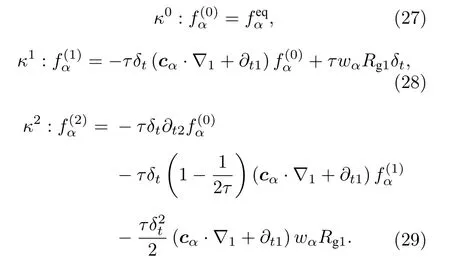
對(28)式與(29)式分別求零階矩， 并求和后整理變換可得

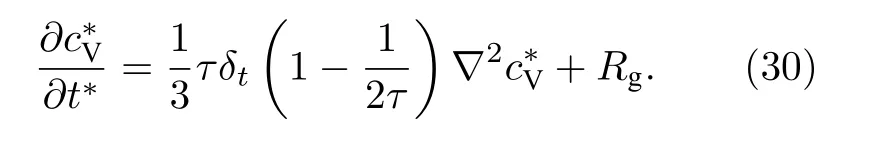
令D*= δt(τ — 0.5)/3， (30)式可以還原為(14)式所示的無量綱載流子質量守恒方程.基于演化方程(20)還原無量綱PB 方程與無量綱Poisson 方程的思路與上述過程相同， 只需按表1 代入不同的源項、平衡分布函數與求解變量表達式即可.

3 計算結果與討論

在LB 模擬中， 可基于實際單位或者格子單位(lattice unit， lu)進行計算， 只要保證在兩個單位體系中控制物理過程的無量綱量相同即可[25].為了便于程序編寫與擴展， 本文采用標準格子單位進行計算(網格步長與時間步長均為1 lu[25])， 計算中長度、時間、電勢、氧空位濃度等可在保證無量綱Debye 長度與無量綱電勢相等的前提下， 在格子單位和實際單位中進行轉換.同時進行網格無關性分析發現， x 方向網格數分別取50 與300 時計算結果差別為0.56%， 分別取400 與300 時計算結果差別為0.008%.由于網格數取300 時計算時間尚可接受， 且考慮到其他工況下可能存在更為劇烈的物理場變化， 本文計算中x 方向網格數取為300.

3.1 PB 方程與Poisson-載流子質量守恒耦合方程對比

如前文所述， PB 方程是載流子電化學勢梯度為零時Poisson-載流子質量守恒耦合方程的一個特解.由于電化學勢梯度是載流子移動從而產生電流的驅動力， 本文分別在離子導體凈電流密度為零與不為零的工況下， 對PB 方程和Poisson-載流子質量守恒耦合方程(若無特殊說明， 下文分別用耦合模型和Present model 在正文和圖中進行指代)的計算結果進行比較.對于導體凈電流密度為零的工況， 為了進一步和文獻結果進行對比驗證，采用Mott-Schottky 長度lMS作為特征長度， 計算和邊界條件與文獻[18]相同.如圖2(a)所示， 本文發展的PB 方程LB 模型和耦合方程LB 模型的計算結果與文獻[18]求解PB 方程的計算結果幾乎完全重合， 驗證了本文數學模型和數值方法的準確性， 同時說明凈電流密度為零時， PB 方程與耦合方程具有相同的計算結果.需要說明的是， 由于采用相同的控制方程和數值方法， 圖2(a)同樣能夠說明本文發展的模型在導體凈電流密度不為零時的較好可靠性.

圖2(b)與圖2(c)為導體凈電流密度不為零時，PB 方程與耦合方程的計算結果比較.計算工況中控制載流子傳輸過程的無量綱參數為zVFφ0/(RT) =2， λD/x0= 0.1763.計算邊界條件為: x/x0= 0 時，iB/i0= —0.1; x/x0= 1 時， cV/cV0= 1， φ/φ0= 0.與耦合模型相比， PB 方程計算出趨勢相反的電勢分布和氧空位濃度分布， 并導致不同的電荷密度以及電流密度分布.同時， PB 模型計算所得SCL 電阻與厚度分別為—0.173 與0.715， 顯著區別于耦合模型的計算結果(SCL 電阻與厚度分別為1.670 與0.485).需要說明的是， 在確定SCL 厚度時， 考慮到計算和數值精度等影響， 取擴散電流密度idif/i0變化至小于10—3量級的位置作為區分體相和SCL的邊界以確定SCL 厚度， 可見文中SCL 厚度為一個近似值， 與采用的誤差等級相關聯(本文取為10—3)， 但是本文重點研究無量綱參數對SCL 厚度的影響規律， 因此只要采用統一的誤差等級， 就有比較意義.注意到兩種模型計算的SCL 電阻具有不同符號， 是因為PB 模型計算所得氧空位濃度大于等于1 (圖2(b))， 而耦合模型計算所得氧空位濃度小于等于1 (圖2(c))， 由(16)式可以得出， PB模型與耦合模型計算的SCL 電阻分別小于零與大于零.同時分析PB 模型計算的電流密度分布發現(圖2(b))， 僅在界面(x/x0= 0)及其附近區域存在變化的凈電流密度， 其他區域導體凈電流密度恒為零， 該結果顯然違背了電荷守恒定律， 且不符合iB/i0= —0.1 的電流密度邊界條件.上述計算結果比較直觀地證明了PB 方程只適用于凈電流密度為零的工況.

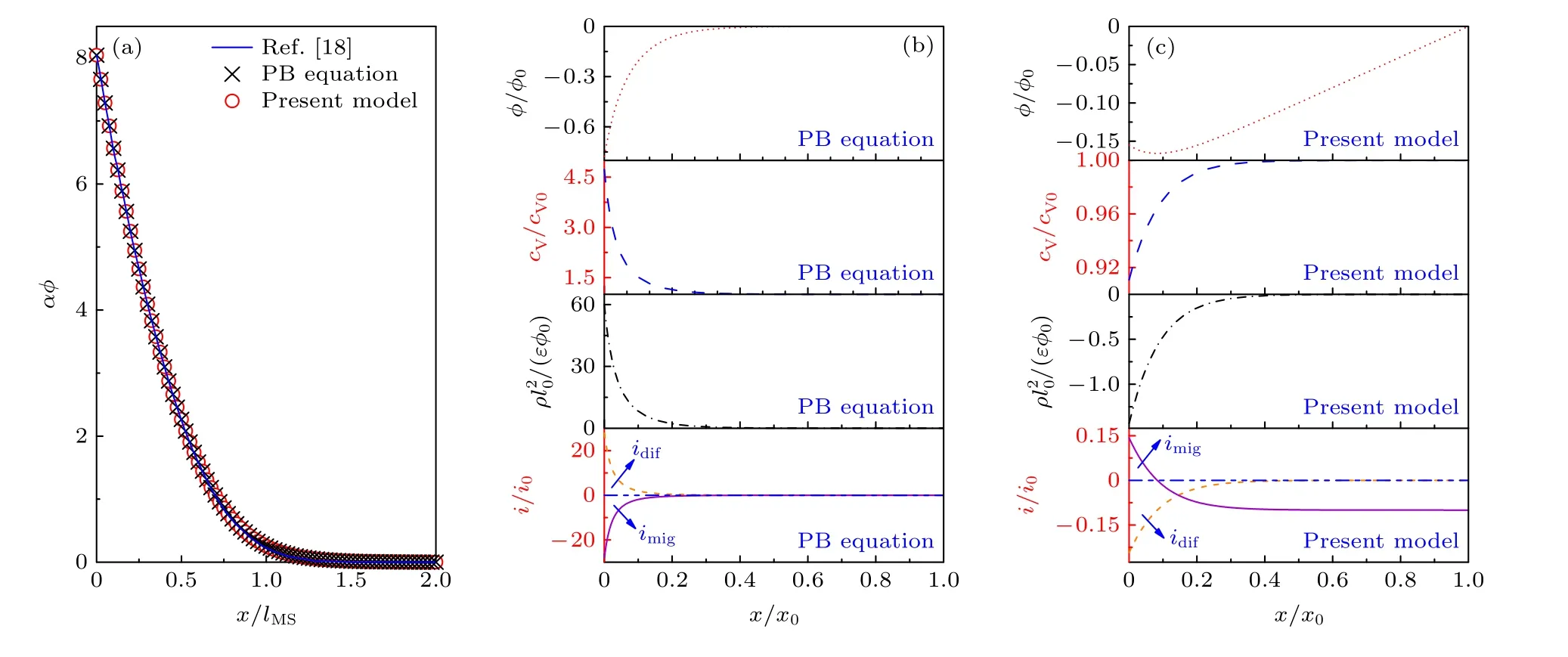
圖2 Poisson-載流子質量守恒耦合方程(Present model)與PB 方程(PB equation)的計算結果比較 (a)導體凈電流密度為0 時，本文發展的PB 方程LB 模型與耦合方程LB 模型的計算結果與文獻[18]求解PB 方程獲得的計算結果比較， 其中α = F/(RT)，lMS = [φ(0)ε0εr/(FcV0)]0.5; (b)， (c)導體凈電流密度不為0 時的計算結果Fig.2.Comparison of the results predicted by the coupled Poisson and charge carrier mass conservation equation (Present model)and the PB equation.(a) The net current density is 0.Results predicted by the PB equation from Ref.[18] is also presented for the comparison purpose.Here， α = F/(RT) and lMS = [φ(0)ε0εr/(FcV0)]0.5.(b)， (c) Results of the case that the net current density is not 0.

分析圖2(c)所示的耦合模型計算結果， 沿著導體厚度方向， 氧空位濃度逐漸增大至體相保持不變， 且增大的速率不斷減小， 因此 ? (cV/cV0)大于零且不斷減小至零， 導致擴散電流密度idif/i0小于零且逐漸增大至體相為零.電勢在體相線性增大， 在SCL 呈現下凹的非線性變化規律， 數值在x/x0=0.085 時達到最小值， 因此當0 ≤ x/x0≤ 0.085時， ? (φ/φ0) ＜ 0， 導致遷移電流密度imig/i0＞ 0;當0.085 ＜ x/x0≤ 1 時， ? (φ/φ0) ＞ 0， 導 致imig/i0＜ 0.由于在體相區域氧空位濃度不變， 且電勢線性變化， 所以imig/i0在體相區域穩定不變;越靠近界面區域， 雖然氧空位濃度不斷減小， 從而導致導體電導率降低， 但電勢梯度不斷增大， 且增大的程度遠大于氧空位濃度減小的程度， 由(8)式與(15)式可知， 遷移電流密度imig/i0是由氧空位濃度與電勢梯度共同決定的， 所以imig/i0的絕對值不斷增大.同時在整個導體區域凈電流密度i/i0=idif/i0+ imig/i0數值恒定為—0.1， 不僅說明電流密度邊界條件實施的正確性， 也證明耦合模型可以在凈電流密度不為零的工況下準確預測載流子傳輸特性.整理方程(1)的源項得到無量綱電荷密度由于F/(ε0εr)～1015， SCL 內極小的氧空位濃度變化都會導致顯著的電勢場變化.由于SCL 內cV/cV0＜ 1，導致無量綱電荷密度小于零且沿著厚度方向不斷增大至體相為零.另外， 除電勢分布外， 氧空位、電荷密度和電流密度都呈現指數變化規律.

3.2 無量綱界面電流密度(iB/i0)的影響

下面研究控制導體內載流子傳輸過程的關鍵無量綱參數的影響規律.基準工況為:1.37 × 10—3， λD/x0= 4.3 × 10—2， iB/i0= —1.圖3 描述了無量綱界面電流密度(iB/i0)對氧空位傳輸過程的影響.隨著iB/i0的增大， 入口界面(x/x0= 0)φ/φ0呈現減小的變化趨勢(圖3(a))， 且沿著導體厚度方向， 靠近界面處φ/φ0的下凹程度越發顯著，但最小值均位于x/x0= 0.05 處(圖3(c))， 導致遷移電流密度imig/i0為零的位置不變， 但界面處的絕對值一直增大(圖3(f)).隨著iB/i0的增大， 界面處氧空位濃度cV/cV0呈現先增大后減小的變化規律(圖3(a))， 且沿著導體厚度方向， 靠近界面處cV/cV0的變化幅度不斷增大(圖3(d))， 導致無量綱電荷密度呈現類似分布(圖3(e))， 擴散電流密度idif/i0的絕對值逐漸增大(圖3(f)).同時發現導體內凈電流密度逐漸增大(圖3(f))， 說明不同iB/i0邊界條件實施的正確性.如圖3(b)所示， 隨著iB/i0的增大， SCL 電阻和厚度均呈現先減小后增大的變化趨勢， 說明在較小電流密度條件下， 適當增大電流密度可促進SCL 內氧空位傳輸; 電流密度較大時， 增大電流密度會使得SCL 內的傳輸阻力增大.

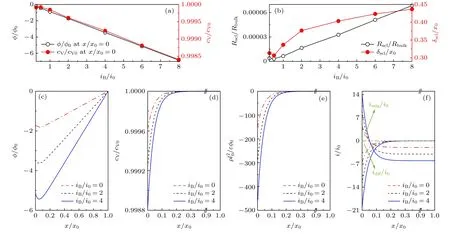
圖3 無量綱界面電流密度(iB/i0)對(a)界面處電勢與氧空位濃度及(b)空間電荷層電阻與厚度的影響; 當iB/i0 = 2， 4， 6 時，(c)導體內電勢、(d)氧空位濃度、(e)電荷密度及(f)電流密度分布Fig.3.Effects of dimensionless current density at the interface (iB/i0) on (a) the potential and oxygen vacancy concentration at the interface， and (b) the resistance and thickness of SCL.Distributions of (c) potential， (d) oxygen vacancy concentration， (e) charge density and (f) current density within the conductor when iB/i0 = 2， 4 and 6， respectively.

3.3 無量綱Debye 長度( λ D/x0 )的影響

對于AO2-M2O3氧離子導體電解質， 不同金屬氧化物和摻雜濃度會導致不同的氧空位濃度cV0以及介電常數ε0εr， 形成具有不同Debye 長度λD的氧離子導體.因此， 金屬氧化物類型和摻雜濃度的影響可通過λD表征.圖4 描述了無量綱Debye 長度(λD/x0)對氧空位傳輸過程的影響規律.λD/x0表征SCL 厚度與離子導體厚度的比值， 該無量綱量可綜合考慮運行溫度T、導體長度x0、不同金屬氧化物和摻雜濃度引起的不同介電常數ε0εr與氧空位濃度cV0等參數對載流子傳輸過程的影響.如圖4 所示， 由于入口界面電流密度相等且導體整體電中性， 所以隨著λD/x0增大， 沿著x 軸反方向， 電荷密度會在較大厚度內由0 更為緩和地減小， 導致入口界面電荷密度絕對值更小(圖4(e))， 由Poisson 方程可得，電勢分布曲率更小(圖4(c))， 因此入口電勢不斷增大(圖4(a))， 由于電勢梯度更小， 遷移電流密度絕對值也會減小(圖4(f)).同時， 由電荷密度公式可得， 隨著λD/x0增大， 入口界面氧空位濃度不斷減小(圖4(a))， 導致濃度在更大厚度內由1 更緩慢地減小(圖4(e))， 呈現更小的濃度梯度， 引起更小的擴散電流密度絕對值(圖4(f)).如圖4(b)所示，SCL 電阻和厚度均隨著λD/x0的增大而增大， 且SCL 厚度大于Debye 厚度.另外， 當λD/x0= 0.1 時，δscl/x0已經接近0.8， 由于SCL 厚度δscl不會超過導體厚度x0， 即δscl/x0＜ 1， 因此本文不再探討λD/x0＞ 0.1 時其對SCL 內氧空位傳輸過程的影響規律.在氧離子導體界面調控技術中， 可通過合理地選擇金屬氧化物和調整摻雜濃度以獲得不同導體材料(體現為改變介電常數ε0εr與氧空位體相濃度cV0等)、改變運行溫度(體現為改變T )和幾何結構(體現為改變x0)等， 以有效地改變界面電阻， 從而調控整個導體的導電性能.

3.4 無量綱電勢( z VF φ0/(RT) )的影響

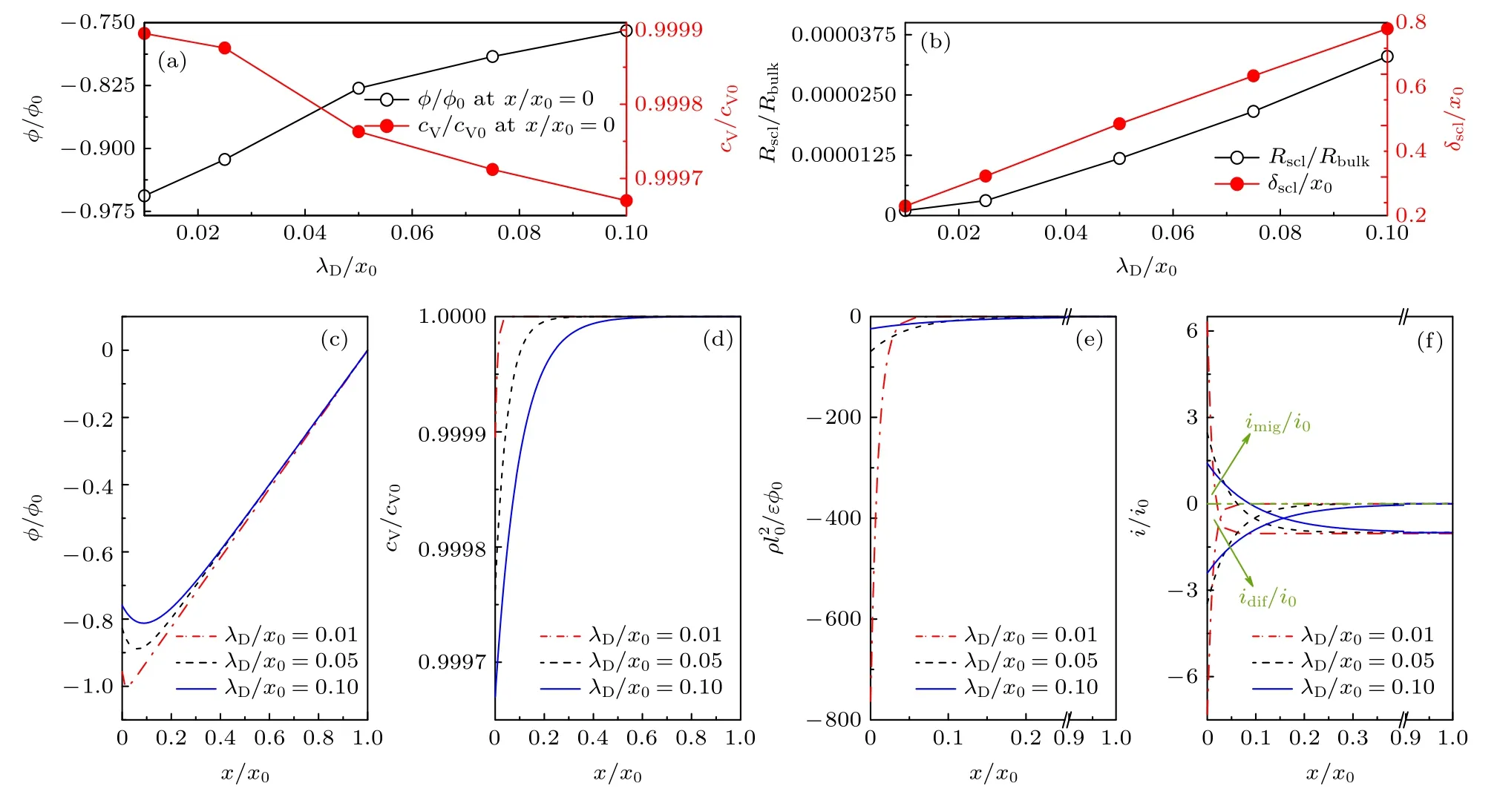
圖4 無量綱Debye 長度(λD/x0)對(a)界面處電勢和氧空位濃度及(b)空間電荷層電阻與厚度的影響; 當λD/x0 = 0.01， 0.05，0.1 時， (c)導體內電勢、(d)氧空位濃度、(e)電荷密度及(f)電流密度分布Fig.4.Effects of dimensionless Debye length (λD/x0) on the (a) potential and oxygen vacancy concentration at the interface， and(b) the resistance and thickness of SCL.Distributions of (c) potential， (d) oxygen vacancy concentration， (e) charge density and(f) current density within the conductor when λD/x0 = 0.01， 0.05 and 0.1， respectively.

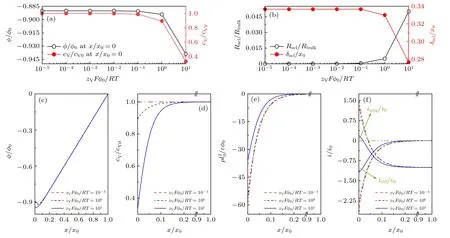
圖5 無量綱電勢(zVFφ0/(RT))對(a)界面處電勢和氧空位濃度及(b)空間電荷層電阻和厚度的影響; 當zVFφ0/(RT) = 10—3，1 與10 時， (c)導體內電勢、(d)氧空位濃度、(e)電荷密度及(f)電流密度分布Fig.5.Effects of dimensionless potential (zVFφ0/(RT)) on (a) the potential and oxygen vacancy concentration at the interface， and(b) the resistance and thickness of SCL.Distributions of (c) potential， (d) oxygen vacancy concentration， (e) charge density and(f) current density within the conductor when zVFφ0/(RT) = 10—3， 1 and 10， respectively.

圖5 描述了不同無量綱電勢(zVFφ0/(RT ))下的氧空位傳輸特性.zVFφ0/(RT )反映了驅動氧空位移動的過電勢和熱勢之比.增大zVFφ0/(RT )意味著導體兩端的電勢差更大， 因此入口電勢呈現減小的變化趨勢(圖5(a)); 同時從圖5(c)可得， 沿著導體厚度方向， 入口處電勢分布更為平緩， 意味著電勢分布曲率更小， 由Poisson 方程可得， 對應的電荷密度絕對值也會更小(圖5(e))， 且入口氧空位濃度也會降低(圖5(a)與圖5(d)).由于隨著zVFφ0/(RT )的增大， 入口界面區域電勢分布的梯度減小(圖5(c))， 導致遷移電流密度絕對值減小(圖5(f)); 氧空位濃度梯度大于零且不斷增大， 但是其增大幅度小于zVFφ0/(RT )增大幅度， 導致擴散電流密度絕對值不斷減小(圖5(f)).SCL 電阻呈現和氧空位濃度相反的變化趨勢， 且SCL 厚度隨著zVFφ0/(RT )的增大而減小(圖5(b)).同時， 從圖5 可以發現， 當zVFφ0/(RT ) ≤ 0.1 時，zVFφ0/(RT )對導體內氧空位遷移與擴散過程的影響幾乎可忽略; zVFφ0/(RT ) ＞ 0.1 時， 其對載流子傳輸特性影響顯著.因此， 當過電勢大于熱勢時，zVFφ0/(RT )增大會顯著增大界面傳輸阻力， 當利用界面空間電荷層效應來調控材料性能時， 需謹慎選擇材料、制備和運行條件， 使得zVFφ0/(RT )位于顯著改變SCL 傳輸特性區域.

4 結 論

晶界與異質界面等導致的空間電荷層效應， 被證明可顯著改變離子導體內氧空位傳輸能力.尤其對于廣受關注的納米導體材料， 通過引入界面產生空間電荷層效應來控制材料性能， 是目前公認的行之有效的技術手段之一.PB 方程是現階段應用最為廣泛的描述SCL 內載流子傳輸過程的數學模型，但其受限于載流子電化學平衡(即電化學勢梯度為零)的基本假設， 無法準確捕捉廣泛應用于電化學器件的離子導體在運行工況下(即電化學勢梯度不為零且存在凈電流密度)的傳輸能力.本文著重研究了考慮空間電荷層效應時， 具有凈電流密度的氧離子導體內載流子傳輸特性.

首先建立了Poisson 方程與載流子質量守恒方程耦合的數學模型， 推導了控制氧離子導體SCL 內氧空位遷移與擴散過程的無量綱參數.通過與該耦合模型對比， 定量證明了在氧離子導體具有凈電流密度時， PB 模型無法合理預測導體內載流子傳輸過程.進一步基于耦合模型， 獲取了關鍵無量綱參數的影響規律: 1)增大界面電流密度， 導體兩端電勢差增大， 界面氧空位濃度先增大后減小， SCL 電阻和厚度先減小后增大.2)當無量綱Debye 長度(λD/x0)取值使得SCL 厚度小于導體厚度時， 增大λD/x0， 導體兩端電勢差、界面氧空位濃度顯著減小， 而SCL 電阻與厚度則呈現增大的變化趨勢.3)對于無量綱電勢(zVFφ0/(RT ))， 當過電勢與熱勢數量級相差不大時(本文中大于0.1)， 增 大zVFφ0/(RT )， 導 體 兩 端 電 勢 差 與SCL 電阻增大， 而界面氧空位濃度與SCL 厚度減小; 當過電勢遠小于熱勢時， 改變zVFφ0/(RT )對氧空位傳輸過程影響可忽略.以上結論可為有效地通過界面設計以改善氧離子導體性能提供理論支撐.