面向近原子尺度制造的光學(xué)測量精度極限分析*

戰(zhàn)海洋 邢飛 張利

(清華大學(xué)精密儀器系， 北京 100084)

1 引 言

高精度制造在國家科技和經(jīng)濟發(fā)展中發(fā)揮著重要作用.隨著科技的發(fā)展， 制造技術(shù)的精度跨越了毫米、微米尺度， 進入納米量級.以量子理論為基礎(chǔ)的原子及近原子尺度制造是下一代制造技術(shù)的主流發(fā)展方向[1，2]， 而納米級甚至更高精度的測量技術(shù)是原子制造技術(shù)發(fā)展的基礎(chǔ)和保障.光學(xué)測量具有精度高、測量范圍廣、測量直觀等優(yōu)點， 雖然具有百納米級的衍射極限限制， 但此極限僅針對兩個相鄰目標的辨識問題， 對單個成像光斑中心的測量可以達到更高精度.如2014 年諾貝爾化學(xué)獎授予的光激活定位顯微技術(shù)(photoactivated localization microscopy， PALM)， 通過對細胞內(nèi)的單分子進行分時點亮定位， 實現(xiàn)了對活細胞中單分子的超越衍射極限的成像測量[3，4].顯微領(lǐng)域利用相關(guān)技術(shù)， 實現(xiàn)了對DNA、溶酶體、線粒體等微小細胞結(jié)構(gòu)的清晰成像[5-8]和對膜上單分子運動等動態(tài)過程的納米級測量[9-11]， 這對理解具有原子級結(jié)構(gòu)特征及裝配精度的細胞的內(nèi)部機理具有重要意義， 為復(fù)雜原子功能結(jié)構(gòu)的制造奠定了基礎(chǔ)[1].光學(xué)測量也廣泛應(yīng)用于超精密加工制造領(lǐng)域.在用于加工高端芯片的光刻機中， 通過測量晶圓反射光成像點確定晶圓的固定位置[12]， 直接影響著芯片的加工精度.美國噴氣推進實驗室(jet propulsion laboratory， JPL)先后使用激光靜態(tài)和動態(tài)干涉條紋對圖形探測器像素偏移進行測量， 達到微像素級標定精度[13-15].原子力顯微鏡(atomic force microscopy， AFM)通過測量激光光斑的中心位置，計算懸臂梁發(fā)生的微位移， 以實現(xiàn)近原子尺度的測量精度[16].光學(xué)測量也是AFM 校準如溫漂誤差的測量及補償中重要的技術(shù)手段[17].

雖然對單個成像目標中心位置的測量不受衍射極限的直接制約， 但根據(jù)量子力學(xué)理論， 成像過程中探測器上產(chǎn)生的光電子數(shù)是波動的， 此波動被描述為散粒噪聲(shot noise)， 服從泊松分布[18].散粒噪聲和探測器暗電流噪聲等隨機噪聲的存在決定了由灰度響應(yīng)估計像中心位置的過程中， 測量精度不可能達到無限高.Winick[19]基于克拉美羅下界(Cramer-Rao lower bound， CRLB)理論推導(dǎo)了特定形式下的點目標像的測量精度極限， 其適用于像斑點擴散函數(shù)(point spread function， PSF)為高斯函數(shù)的情況.Wang 等[17，20]學(xué)者對固連在儀器上的微球進行成像以精確測量儀器運動， 討論了微球尺寸等參數(shù)對成像強度分布和測量精度的影響， 但沒有完整地從統(tǒng)計學(xué)的角度建立這些參數(shù)和測量精度的直接定量關(guān)系.

針對以上背景和問題， 本文基于CRLB 理論等前人工作， 發(fā)展了適用于任意強度分布成像的光學(xué)測量精度極限計算方法， 并以典型點目標光斑艾里斑為例， 分析了光強、波長、光學(xué)系統(tǒng)相對孔徑、探測器噪聲等參數(shù)與光學(xué)測量極限的定量關(guān)系， 給出了適用于類似艾里斑的PSF 的提高測量精度的建議.對于PSF 和艾里斑有較大差異的， 也可使用本文方法進行推導(dǎo)分析.對測量極限的定量分析，為原子及近原子尺度制造過程中光學(xué)測量方式的應(yīng)用和優(yōu)化， 提供了分析方法和理論指導(dǎo).

2 精度極限分析方法

2.1 任意強度分布的二維定位精度極限

由目標發(fā)出的光經(jīng)過光學(xué)系統(tǒng)打在探測器上，形成灰度響應(yīng).若不考慮量子效率， 像素 ( i，j) 由光信號產(chǎn)生的光電子數(shù)為

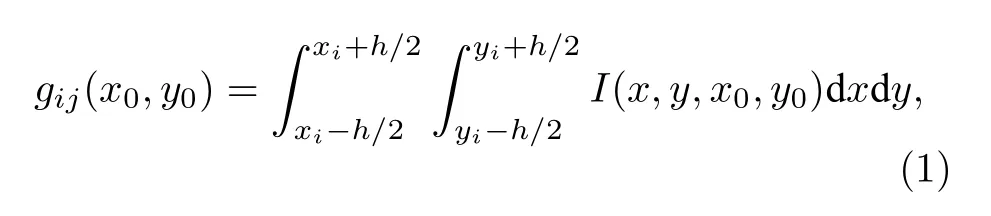
其中， I (x，y，x0，y0) 為到達探測器上的任意光強分布， 單位為每平方微米內(nèi)的光電子數(shù); ( x0，y0) 為探測器上像斑的中心; ( x，y) 為探測器上的任意位置; ( xi，yi) 為像素 ( i，j) 的中心位置; h 為矩形像素尺寸(邊長)， 單位均為μm.由于散粒噪聲的存在，gij(x0，y0) 實際上為像素 ( i，j) 上的光電子數(shù)均值，而此光生電子數(shù)服從泊松分布[18].

以CCD 或CMOS 探測器為例， 根據(jù)其像素響應(yīng)標準模型[18]， 像素 ( i，j) 產(chǎn)生的光電子數(shù)有一部分來自于暗信號， 而暗電流噪聲主要由曝光時間內(nèi)電子的熱運動產(chǎn)生， 也服從泊松分布， 假設(shè)此噪聲均值和方差為.故在像斑中心為 ( x0，y0) 的情況下， 像素 ( i，j) 產(chǎn)生光電子數(shù)為 sij的概率密度函數(shù)為

進而使得探測器局部區(qū)域A 產(chǎn)生光電子數(shù)矩陣S 的聯(lián)合概率密度函數(shù)為

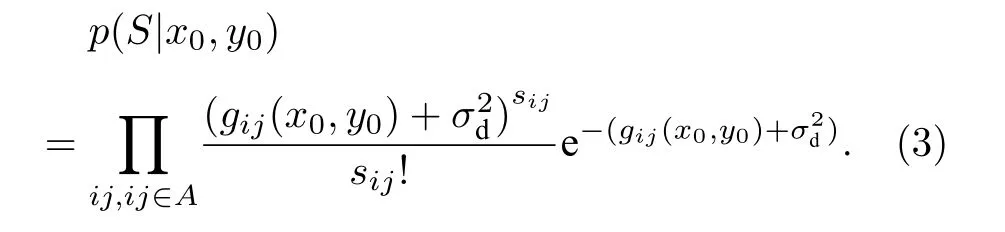
其中局部區(qū)域A 可以任意選取， 可以將像斑分布的所有像素全部囊括， 也可以根據(jù)具體強度分布選取特征最明顯的像斑局部.

CRLB 是數(shù)理統(tǒng)計領(lǐng)域進行參數(shù)估計時任何無偏估計方法都不能低于的方差[21-23].文獻[19]對高斯強度分布的CRLB 進行了推導(dǎo)， 為進行化簡在過程中使用了兩個條件， 分別是

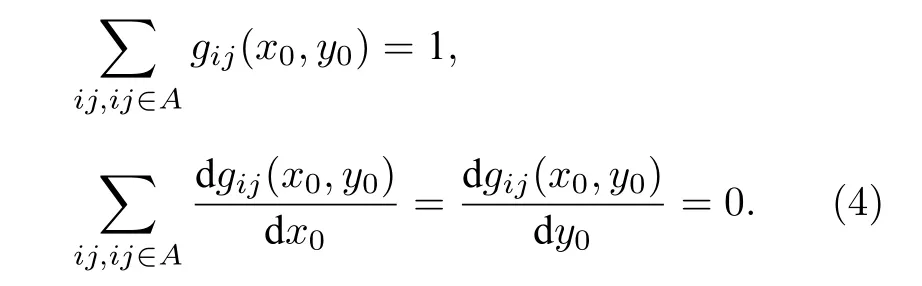
此處區(qū)域A 內(nèi)的像素產(chǎn)生的光電子數(shù)和為1， 是因為文獻中對 gij(x0，y0) 進行了歸一化操作.(4)式成立的條件是區(qū)域A 包含了像斑分布的全部像素.考慮到更一般的情況， 即像斑較大或較復(fù)雜時， 只用特征明顯和信噪比高的區(qū)域可能會獲得更高的精度.因此本文在(4)式不成立的條件下， 推導(dǎo)任意強度分布的精度極限.

根據(jù)CRLB 的計算過程[19]

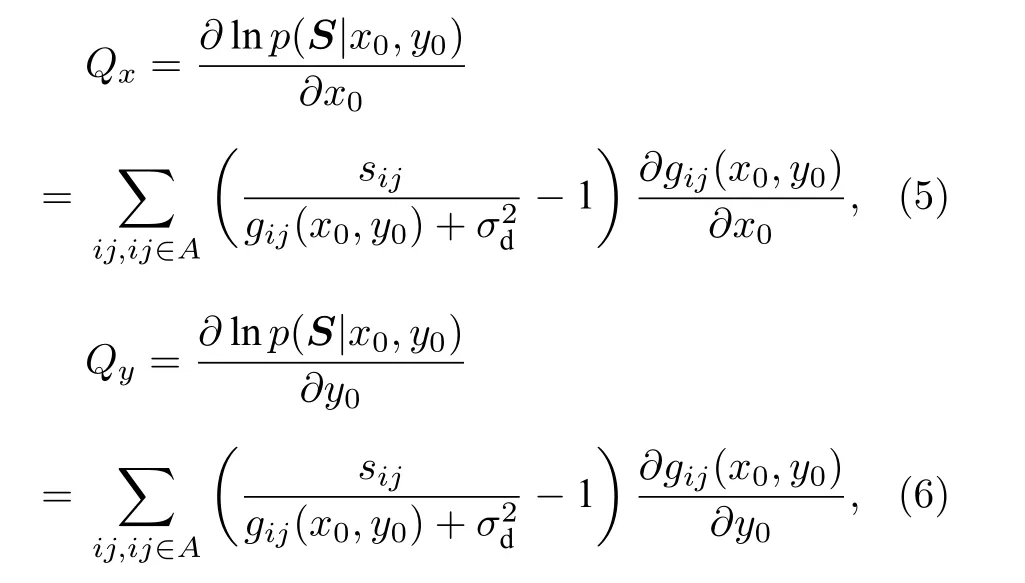
其中， Qx和 Qy代表(3)式的對數(shù)對 x0和 y0的偏導(dǎo).分別計算和 QxQy的數(shù)學(xué)期望

由于

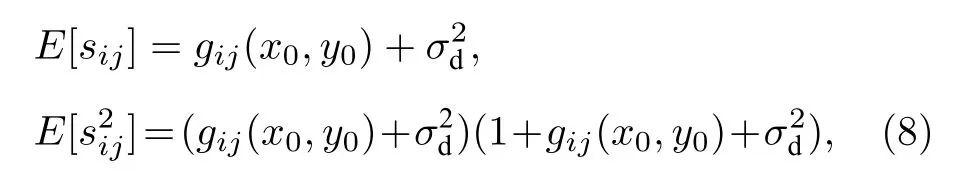
且 sij與 smn，mn/=ij相互獨立， 因此(7)式的第二項數(shù)學(xué)期望為0， 對第一項的數(shù)學(xué)期望進行計算， 化簡得

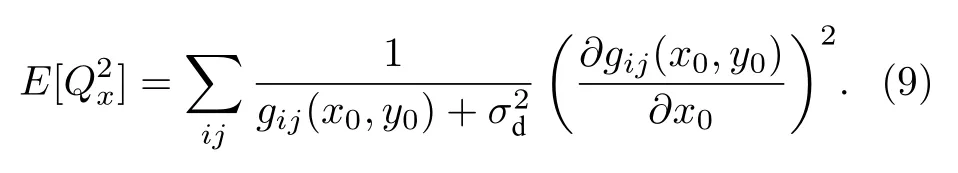
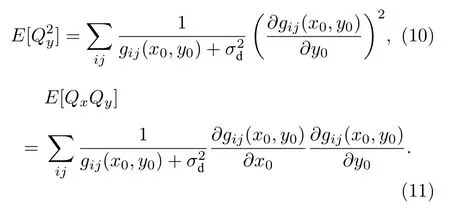
在估計像斑中心橫坐標 x0時的CRLB 為

將(9)—(11)式代入(12)式即可得到最終結(jié)果.縱坐標 y0的CRLB 同理， 只需將(12)式的 x 和 y 下標調(diào)換順序.如(1)式所示， gij(x0，y0) 可由任意光強分布函數(shù)積分獲得，可通過查探測器參數(shù)或由光子轉(zhuǎn)移法計算得到[18，24].另外， 由于CRLB 反映的是方差的下界， 在本文中取根號值， 即標準差下界， 并稱其為無偏估計方法的精度極限.

2.2 艾里斑模型

光學(xué)成像系統(tǒng)的光瞳多呈圓形， 正入射時， 圓孔的夫瑯禾費衍射斑為艾里斑， 其強度分布公式為

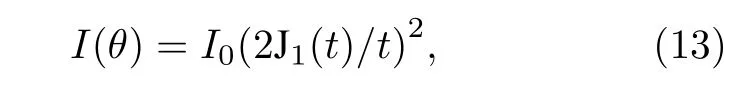
式中

其中， θ 為衍射角， D 為光瞳直徑， λ 為波長; I0為中心強度; J1(t) 為一階貝塞爾函數(shù).假設(shè)在像平面上點 ( x，y) 距離像斑中心 ( x0，y0) 為 r ， r 可近似為

其中 f 為光學(xué)系統(tǒng)焦距， 則

這里， F 為鏡頭F 數(shù)， 即焦距與光瞳直徑之比.將(16)式代入(13)式中， 即可得到像面上的光強分布函數(shù)

將(17)式代入(1)式， 即可得到 gij(x0，y0) ， 進而根據(jù)(12)式， 可計算不同參數(shù)與精度極限之間的關(guān)系.圖1 給出了艾里斑的光強分布函數(shù)和像素灰度響應(yīng)的示例， 兩個灰度響應(yīng)的差異是因為像斑中心落在了像素內(nèi)的不同位置.

圖1 艾里斑的光強分布函數(shù)及相應(yīng)的像素灰度響應(yīng)示例Fig.1.Intensity function of an Airy spot and its corresponding pixel response.

3 艾里斑光學(xué)測量精度極限分析

3.1 能量與噪聲

像斑的能量、散粒噪聲、探測器暗電流噪聲是影響圖像信噪比的參數(shù).由(12)式， 這些噪聲和能量耦合在一起， 無法通過單個或多個像素的信噪比直接對精度極限進行評估.因此通過仿真的方式，對表征像斑能量和散粒噪聲的 I0， 表征暗電流噪聲的進行分析.

仿真條件為F 數(shù)取4， 像素尺寸為2 μm， 波長為500 nm， 中心強度為400 光子數(shù)/μm2， 暗電流噪聲分別設(shè)置為0 和25 (如果探測器光電子轉(zhuǎn)灰度的增益為0.2， 則=25 對應(yīng)的灰度值標準差為1).由(12)式， 精度極限與像斑中心的位置有關(guān).將像斑中心分別均勻落在一個像素的不同位置內(nèi)， 計算對像斑橫坐標 x0估計的精度極限.其中像斑中心相對于像素邊緣的位置， 稱為像素相位.仿真結(jié)果如圖2 所示， 精度極限和像素相位的關(guān)系為一個復(fù)雜的曲面， 無暗電流噪聲時， 在此仿真條件下， 定位精度極限約為0.013 像素， 暗電流噪聲的出現(xiàn)使得精度極限變差.

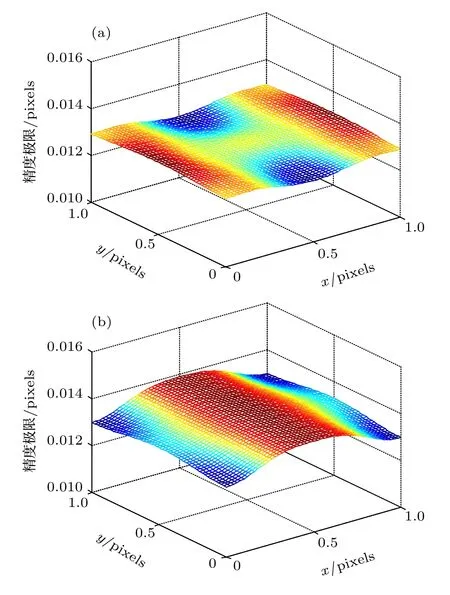
圖2 精度極限-像素相位曲面 (a) 中心強度為400， 暗電流噪聲為0; (b) 中心強度為400， 暗電流噪聲為25Fig.2.Relationship of the precision limit to the x and y pixel phase: (a) The central intensity is 400， the dark current noise is 0; (b) the central intensity is 400， the dark current noise is 25.

進一步地， 取y 像素相位為0.5 的截面， 分別在 I0=400 ，=0， 25， 100， 400 和I0=400， 800，1600， 3200 ，=400 的條件下計算x 方向精度極限與x 方向像素相位的曲線并進行對比， 結(jié)果如圖3 所示.固然像斑能量越高， 暗電流噪聲越小，精度極限越好.值得注意的是， 當暗電流噪聲不可忽略而像斑能量又不夠高時， 精度極限曲線的波動幅度變大， 這意味著像斑中心位于像素中心和位于像素邊緣時定位精度有較大的差異， 在像素邊緣處能夠?qū)崿F(xiàn)更高的定位精度.

圖3 y 像素相位為0.5 時的精度極限-x 像素相位曲線(a) 中心強度為400， 暗電流噪聲分別取0， 25， 100， 400; (b) 暗電流噪聲為400， 中心強度分別取400， 800， 1600， 3200Fig.3.Relationship of the precision limit and the x pixel phase when the y pixel phase is 0.5: (a) The central intensity is 400， the dark current noise is 0， 25， 100， 400， respectively; (b) the dark current noise is 400， the central intensity is 400， 800， 1600， 3200， respectively.

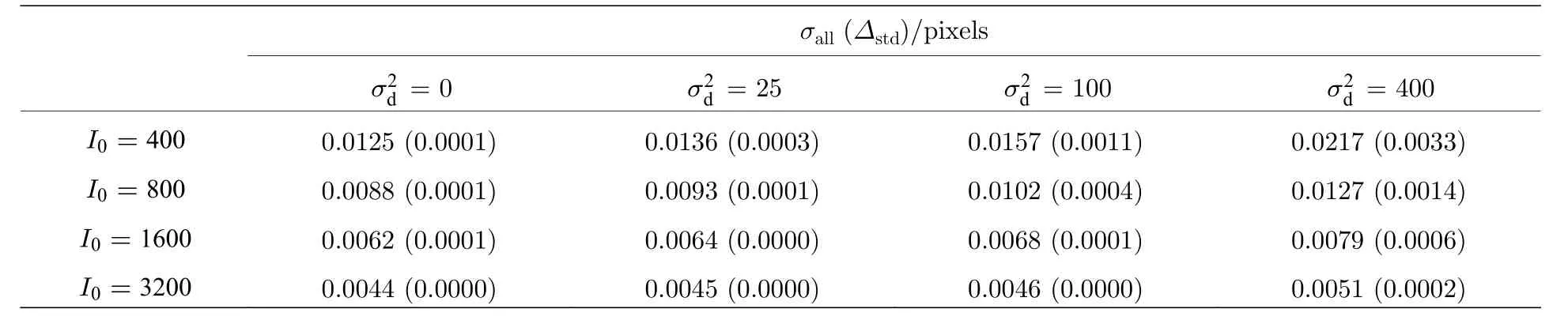
表1 不同能量和噪聲條件下σall 和Δstd 結(jié)果(保留小數(shù)點后四位)Table 1.Results of σall and Δstd under different levels of spot energy and noise.

由此可以看出， 研究精度極限不僅需要關(guān)注整體的精度情況， 還要研究精度極限隨像素相位的波動程度.為方便分析， 對于如圖2 所示的精度極限曲面， 定義兩個指標σall和Δstd， 其中σall為精度極限曲面所有值的均方根(root mean square， RMS)，反映像斑中心均勻分布在各個像素相位的情況下對精度極限的整體期望， Δstd為精度極限曲面所有值的標準差， 反映其隨像素相位的波動程度.對不同像斑能量和暗電流噪聲計算這兩個指標， 結(jié)果如表1 所列.可以看出， 當暗電流噪聲為0 時， 能量每增大 n 倍， 精度會提高倍; 當暗電流噪聲變大時， 總體精度極限σall變差， 精度極限隨像素相位波動Δstd也會變大.由(9)式可知， 暗電流噪聲的作用相當于均勻抬高了灰度分布函數(shù) gij(x0，y0).

總結(jié)來說， 探測器暗電流噪聲很小時， 像斑能量增大 n 倍， 精度極限提高倍.隨著暗電流噪聲變大， 總體精度極限變差， 精度極限隨像素相位的波動也顯現(xiàn)出來并逐漸變大.為盡量減少暗電流噪聲的影響， 應(yīng)使像斑中心位于像素邊緣.當F 數(shù)為4， 像素尺寸為2 μm， 波長為500 nm， 中心強度為400 光子數(shù)/μm2， 暗電流噪聲方差為25 (探測器增益為0.2 時其對應(yīng)的灰度值標準差為1)， x0定位的總體精度極限為0.014 像素(28 nm)， 像素中心位置有最差精度0.014 像素(28 nm)， 像素邊緣位置有最優(yōu)精度0.013 像素(26 nm).當暗電流噪聲方差變?yōu)?00 (對應(yīng)灰度值標準差為2)時， 總體精度極限變?yōu)?.016 像素(32 nm)， 最差精度變?yōu)?.017 像素(34 nm)， 最優(yōu)精度變?yōu)?.014 像素(28 nm).

3.2 F 數(shù)、波長和像素尺寸

光學(xué)系統(tǒng)F 數(shù)、光的波長、探測器像素尺寸是影響像斑能量集中程度的參數(shù).為研究像斑集中程度對定位精度極限的影響， 需控制到達探測器上的艾里斑能量總值不變， 而不是中心強度不變.即在變化F 數(shù)和波長的條件下， 保持光強分布函數(shù)在探測器上的積分為常數(shù)， 即

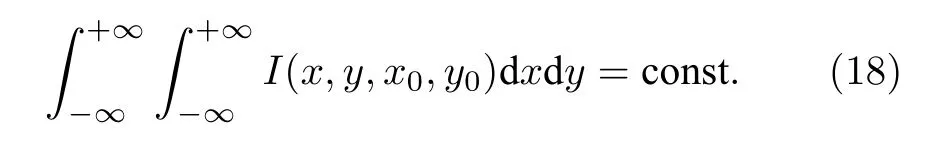
采用圖2(b)中的仿真條件， 保持艾里斑能量總值不變， 將F 數(shù)由4 分別變?yōu)? 和8， 結(jié)果如圖4所示.對比圖2(b)可知， F 數(shù)較小時， 即像斑能量集中時， 精度極限曲面波動很大， 在像素邊緣處取得最優(yōu)定位精度， 但在像素中心位置定位精度很差.而F 數(shù)較大時， 精度極限曲面波動較小， 指標相對于前者來說比較折中.另外， 在估計 x0時y 方向位置影響較小.

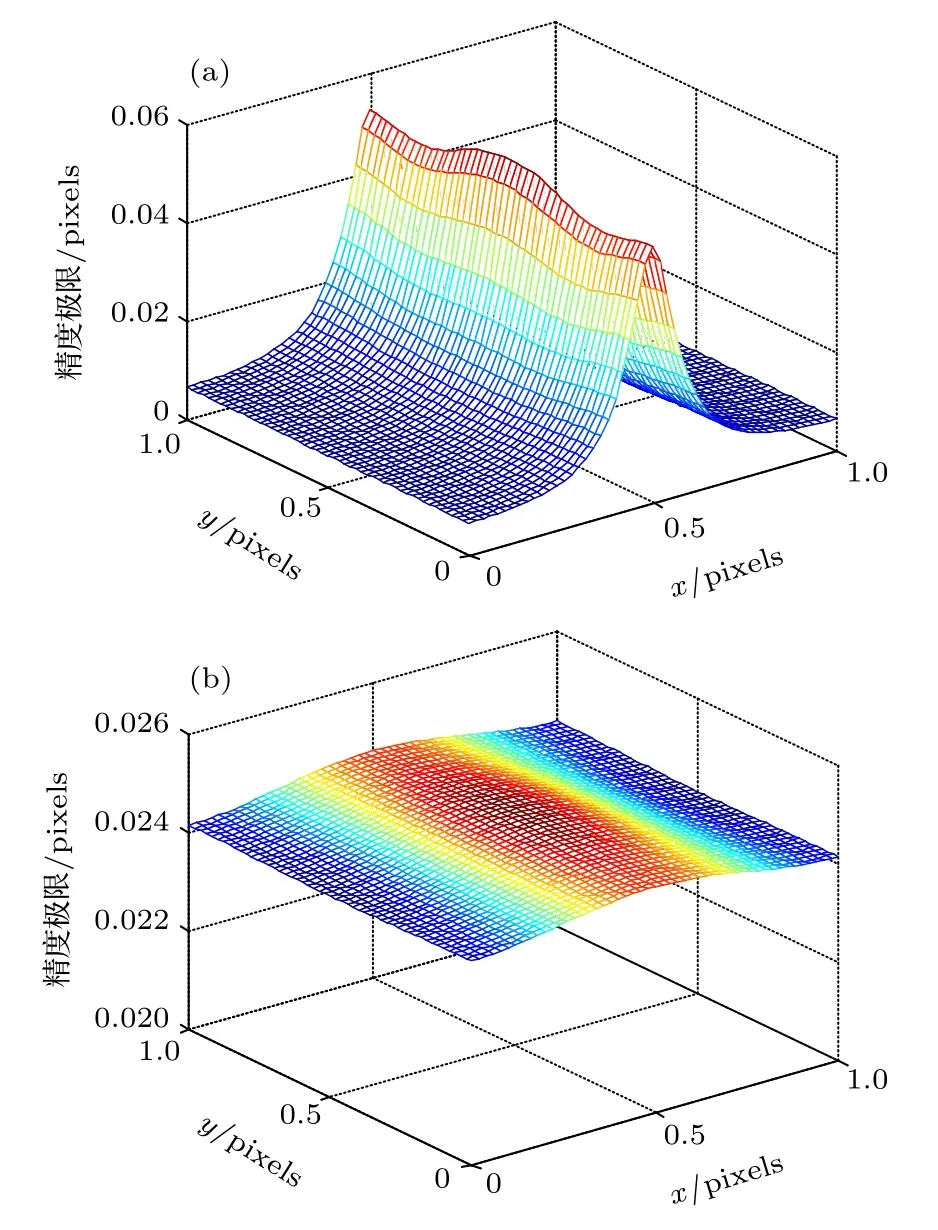
圖4 精度極限-像素相位曲面 (a) F 數(shù)為2; (b) F 數(shù)為8Fig.4.Relationship of the precision limit to the x and y pixel phase: (a) The F of the optical system is 2; (b) the F of the optical system is 8.

進一步地， 由(1)式和(17)式可知， 對于此艾里斑模型， 光學(xué)系統(tǒng)F 數(shù)與波長 λ 對像斑能量集中度有同樣的影響規(guī)律， 如果能量集中度指像面上像斑的大小(以像素為單位)， 則像素尺寸越大， 能量集中度越高.因此定義F 數(shù)和 λ 乘積與像素尺寸h的比值為參數(shù)RF

RF反映了像斑的能量集中度情況， RF越小， 像斑能量集中度越高， 在像面上覆蓋的像素數(shù)越少.即使F 數(shù)、 λ 、 h 發(fā)生改變， 只要RF不變， 則像斑集中程度不變， 精度極限(以像素為單位)不變.在艾里斑能量總值不變的條件下， 改變RF， y 像素相位為0.5 時， x 方向精度曲線和x 像素相位的關(guān)系如圖5 所示.可以看出， RF越小， 在像素邊緣位置定位精度越高， 但犧牲了像素中心位置的精度.而如果追求較好的總體精度指標σall， 應(yīng)該將RF調(diào)到一個適當小的數(shù)值， 在此例中RF為1 左右，σall較好.

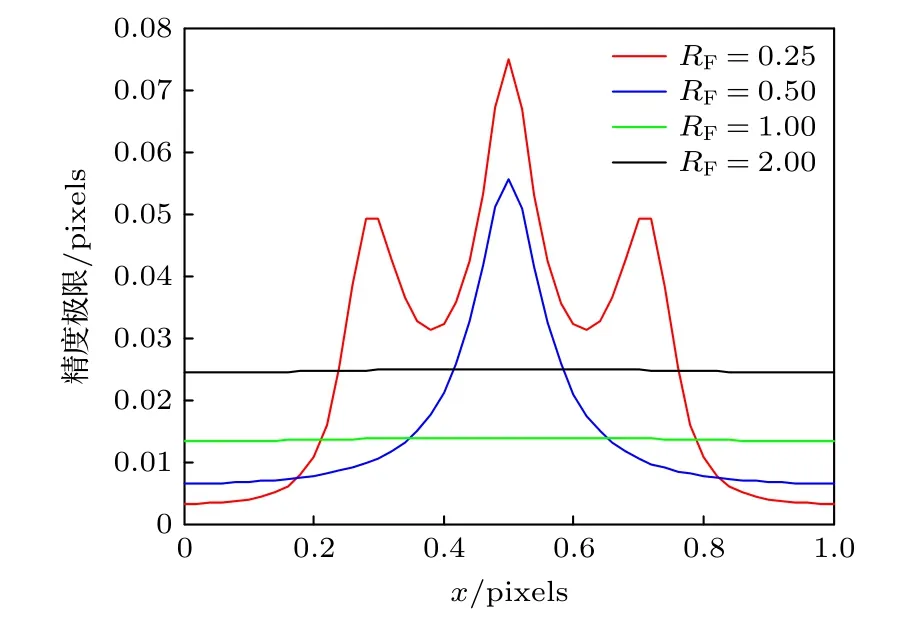
圖5 y 像素相位為0.5 時的精度極限-x 像素相位曲線Fig.5.Relationship of the precision limit and the x pixel phase when the y pixel phase is 0.5.

對不同RF條件下的精度極限曲面的σall和Δstd及像斑中心位于不同像素相位的最優(yōu)精度和最劣精度進行進一步研究.同時RF與衍射極限Δh (單位: 像素)有關(guān)，

將對像斑中心的定位精度與衍射極限進行比較， 結(jié)果如表2 所列.可以看出， RF越小， 雖然總體精度指標較差， 但當像斑中心位于像素邊緣， 可以取到更高定位精度， 在此例信噪比的情況下， 最高定位精度可以達到衍射極限的約100 倍.因此若追求最高定位精度， 在像素尺寸固定的情況下， 盡量減小F 數(shù)和波長的乘積， 并使像斑中心位于像素邊緣.另外， 表2 的結(jié)果單位都為像素， 若保持F 數(shù)和波長的乘積不變， 僅增大像素尺寸， 雖然RF變小， 但在像面上以微米為單位的定位精度并不會變好.可以通過計算發(fā)現(xiàn)， 僅增大像素尺寸， 在像素邊緣處的定位精度(單位: μm)保持同等水平， 其他位置的定位精度(單位: μm)一般會變差.

總結(jié)來說， 衍射極限雖然不直接影響定位精度極限， 但以限制能量集中度的形式， 制約著像斑中心定位的精度極限.適當?shù)哪芰考卸?本例中RF為1 左右)會使得定位總體精度極限最高， 繼續(xù)提高能量集中度會犧牲全量程的總體精度， 而在像素邊緣處獲得更高的局部精度極限.如當F 數(shù)為2， 像素尺寸為2 μm， 波長為500 nm， 中心強度為400 光子數(shù)/μm2， 暗電流噪聲方差為25， 估計 x0的總體精度極限為0.019 像素(38 nm)， 像素中心取得最差精度0.057 像素(114 nm)， 像素邊緣有最優(yōu)精度0.007 像素(14 nm).將F 數(shù)變?yōu)?， 則總體精度極限變?yōu)?.034 像素(68 nm)， 最差精度變?yōu)?.080 像素(160 nm)， 最優(yōu)精度變?yōu)?.003 像素(6 nm).

3.3 計算窗口和計算方式

由(3)式， 局部區(qū)域 A 的選擇也會對定位精度造成影響.取RF= 2， 此時中央亮斑半徑為2.44像素， 其他仿真條件與3.2 節(jié)中相同， 分析不同大小的計算窗口對精度極限的影響.在3.1 和3.2 節(jié)中計算窗口均能包含中央亮斑全部能量， 如圖4(b)窗口設(shè)為11 × 11 像素， 此時分別設(shè)置窗口大小為3 × 3 和5 × 5， 結(jié)果如圖6 所示.當窗口太小涵蓋不到中央亮斑的全部能量時， 精度極限較差.而窗口為5 × 5 和圖4(b)中11 × 11 精度結(jié)果差別不大.

表2 不同能量集中度條件下精度極限結(jié)果Table 2.Results of the precision limit under different levels of spot energy concentration.

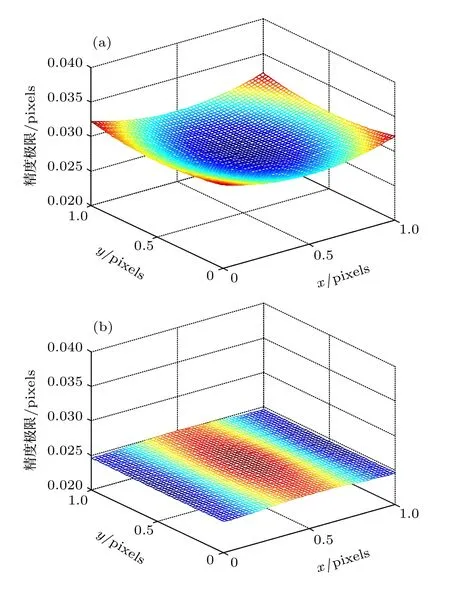
圖6 精度極限-像素相位曲面 (a) 計算窗口為3 × 3;(b) 計算窗口為5 × 5Fig.6.Relationship of the precision limit to the x and y pixel phase: (a) The size of the window used for localization is 3 × 3; (b) the size of the window is 5 × 5.

另外， 在對像斑進行成像或定位過程中， 有時會用到相鄰像素合并(binning)的圖像讀出模式和多次測量定位的平均濾波方法.對于binning 模式，相當于在F 數(shù)和波長固定的情況下， 增大像素尺寸， 對精度的影響關(guān)系可見3.2 節(jié).對于 n 次測量定位的平均濾波方法， 由于其能將隨機噪聲降低到原來的故能將定位精度提高倍.對于3.2 節(jié)結(jié)論中的F 數(shù)為1 的示例， 若采取100 次重復(fù)測量濾波， 在像素邊緣處可獲得0.0003 像素(0.6 nm)的精度極限.

4 實驗像斑的精度極限

在實驗室中進行了點目標成像實驗.點目標光源發(fā)出的光經(jīng)過平行光管進入光學(xué)系統(tǒng)， 在探測器上成像.光學(xué)系統(tǒng)被固定在轉(zhuǎn)臺上， 通過轉(zhuǎn)臺小角度轉(zhuǎn)動， 采集像斑在不同像素相位的灰度值， 以獲得 gij(x0，y0) ， 實驗平臺如圖7 所示.其中光學(xué)敏感器為清華大學(xué)皮型星敏感器， 焦距為25 mm， F 數(shù)為2， 主要敏感波長為400—800 nm， 探測器尺寸為5.3 μm.利用2.1 節(jié)中的任意強度分布像斑精度極限估計方法， 在y 像素相位固定的情況下， 對定位精度極限和x 像素相位的關(guān)系進行計算， 如圖8(a)所示， 右上角為采樣得到的灰度響應(yīng)， 此時能量較為集中， 故在像素邊緣有較好的精度極限.調(diào)節(jié)平型光管端光源的距離， 減少像斑能量集中度， 如圖8(b)所示， 可從右上角的灰度響應(yīng)看出像斑的能量變得發(fā)散了， 此時精度極限曲線變得平緩， 相對于圖8(a)有折中的表現(xiàn).經(jīng)過分析其能量分布不是標準的艾里斑， 但其精度表現(xiàn)仍符合前文對艾里斑分析的定性結(jié)論.即為得到最優(yōu)定位精度極限， 應(yīng)該盡可能提高能量集中度， 并將像斑位于像素邊緣， 或者在測量中更相信邊緣的測量結(jié)果.

圖7 實驗平臺Fig.7.Experiment platform.

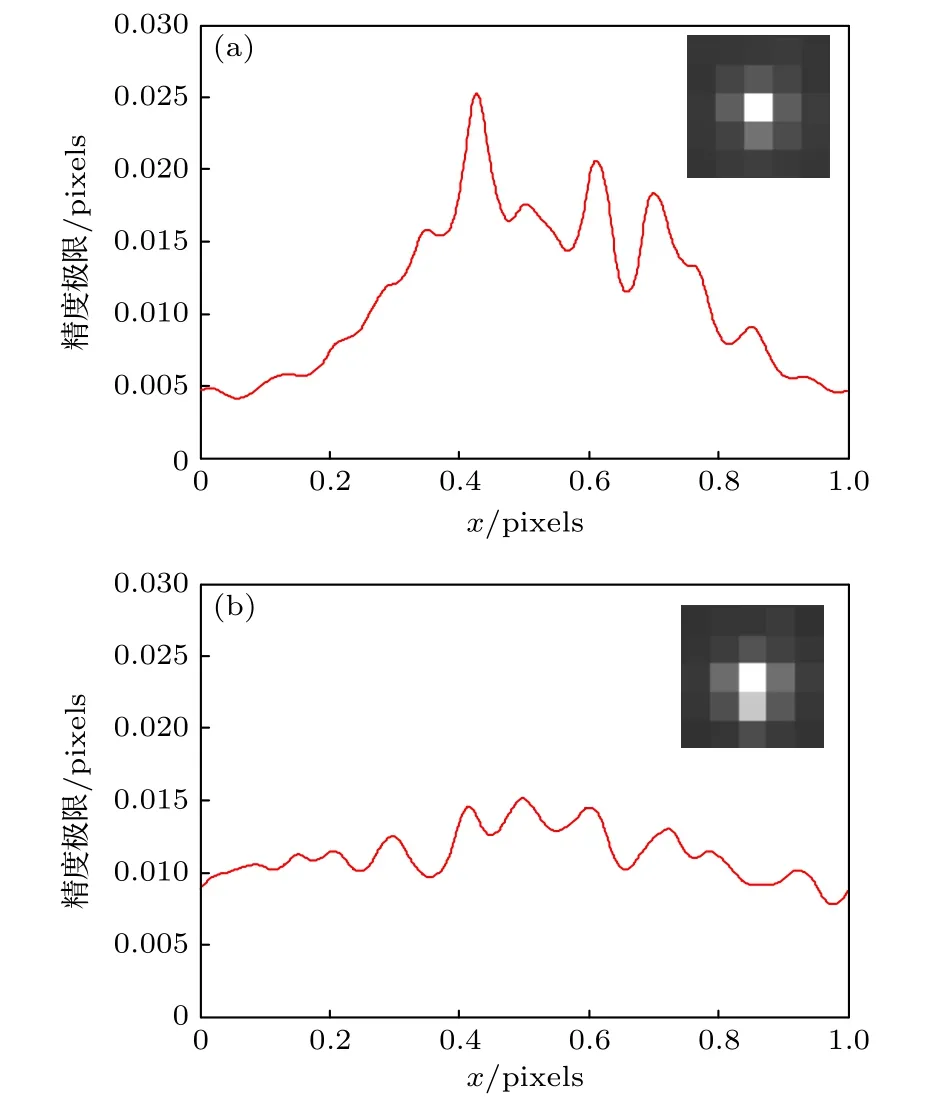
圖8 實驗室像斑的精度極限-x 像素相位曲線 (a) 能量較集中強度分布; (b) 能量較發(fā)散強度分布Fig.8.Relationship of the precision limit and the x pixel phase for laboratory obtained image spots: (a) The precision limit for a energy concentrated spot; (b) the precision limit for a spot with lower energy concentration.

5 結(jié) 論

本文基于CRLB 理論發(fā)展了針對任意強度分布像斑的光學(xué)測量精度極限計算方法， 并以典型光斑模型艾里斑為例， 分析了成像過程中反映信噪比、能量集中度、計算方式的參數(shù)對定位精度的影響規(guī)律， 并得出結(jié)論: 當暗電流噪聲相對較大， 或者像斑能量較集中時， 可使像斑中心移動到像素邊緣進行測量(或更相信像素邊緣處的測量結(jié)果)， 以獲得更好的精度極限; 衍射極限以限制能量集中度的形式制約著像斑中心定位的精度極限， 適當?shù)哪芰考卸葧沟每傮w定位精度極限最高， 繼續(xù)提高能量集中度則會犧牲全量程的總體精度， 提升像素邊緣處的測量精度， 其可以遠超衍射極限; 可使用多次測量的方式減少隨機誤差， 使精度極限達到納米級甚至更高精度.通過實驗驗證了所得結(jié)論對類似艾里斑的像斑同樣有效.對于成像強度分布與艾里斑有較大差異的， 依然可使用本文所述方法進行精度極限分析， 來為原子及近原子尺度制造中光學(xué)測量的應(yīng)用和優(yōu)化提供理論指導(dǎo).