面向三維激波問題的裝配方法

鄒東陽，林敬周，黃潔，劉君

1. 中國空氣動力研究與發展中心 超高速空氣動力研究所，綿陽 621000 2. 大連理工大學 航空航天學院，大連 116024

強擾動在空氣中以超過聲速的速度進行傳播，表現為流體中出現一個參數的間斷面，稱為激波[1]。激波間斷的存在給描述無黏流動的Euler方程的求解帶來了很大挑戰。過去半個多世紀里，為了發展出能夠精確地描述激波的數值方法，科研人員做了大量的工作。如今這些工作是計算流體力學(Computational Fluid Dynamics, CFD)的重要組成部分。根據對激波處理方式的不同，CFD可以分為激波捕捉方法[2-8]和激波裝配方法[9-11]2種。激波捕捉方法是以弱解理論為基礎，全場采用統一的計算方法，無需特殊處理，具有通用性的特點。激波裝配方法則是利用激波關系式(Rankine-Hugoniot，R-H)對激波進行描述，理論上是精確的，但是需要找到匹配激波間斷解與其他光滑區域數值解的方法，存在兼容性的問題。對于復雜激波流動問題，特別是三維問題，激波裝配方法存在應用上的困難。隨著激波捕捉方法的成熟，特別是TVD(Total Variation Diminishing)格式的誕生，對于激波的計算逐步滿足了一定的要求。過去30多年里，激波捕捉方法得到了迅猛發展，在航空航天、汽車建筑、天文地理等領域發揮了巨大的作用。

雖然激波裝配方法的研究在相當長一段時間內寥若晨星，但是其在計算激波時表現出來的優勢還是給許多激波捕捉方法研究提供了思路。像激波裝配方法那樣，將計算網格面與激波面相匹配來減少激波計算誤差的處理手段在很多方法中都得到了應用。在20世紀90年代中期，Parpia和Parikh[12]、van Rosendale[13]以及Camarero[14]等發展了不同的方法，全都是將非結構自適應三角形網格的棱邊與流場中出現的間斷進行匹配。類似的思想在新近發展的間斷伽遼金有限元方法(DG-FEM)中也有一定的體現。兩個完全獨立的研究團隊同時關注于解決網格節點(不包括流場參數)與間斷面相匹配的問題[15-20]。

另外一方面，在過去的十幾年里，CFD工作者對于激波裝配技術的興趣得到了急劇的提升，將目光從激波捕捉方法重新轉向激波裝配方法。造成這一現象的原因主要有2個方面：一是由于CFD工作者在解決激波捕捉方法本質性局限所遇到的困境；二是由于一些研究人員將激波裝配與非結構網格相結合取得了顯著成果，給解決激波捕捉方法所遇到的問題帶來了希望。

意大利學者Paciorri和Bonfiglioli自2006年開始著力于研究基于浸沒邊界法的激波裝配技術。他們方法有效地結合了浮動激波裝配和邊界激波裝配的特點，激波的運動過程中允許其在背景網格上進行(該特點類似浮動激波裝配)，計算過程中通過挖洞構造以激波為內邊界的新的計算網格進行求解(該特點類似邊界激波裝配方法)。Paciorri和Bonfiglioli的方法較傳統的激波裝配方法在靈活性上有了顯著的提高，利用發展的裝配方法成功地解決了若干含有激波構型的問題[21-23]。在國內，劉君等基于非結構動網格技術對激波裝配方法進行了發展，提出了新型非結構激波裝配方法—嵌入式激波裝配方法。嵌入式激波裝配方法中，激波屬于網格的一部分，激波節點的移動帶動其他網格節點的運動，靈活性有了很大提高。該方法被成功用于求解許多定常/非定常流動問題[24-29]。

基于非結構網格的裝配方法在諸多二維問題中的成功應用展示了其相比傳統激波裝配方法在靈活性上的優勢。相比二維問題，三維問題雖然只是增加了一個維度，裝配難度卻是有了大幅度提升。三維空間的激波辨識難度大，給初始激波位置的選擇帶來了困難。描述激波面的網格點在運動過程中彼此要相互匹配，以保證激波收斂運動過程不發散。在三維空間中控制這些點的匹配關系要比二維更為復雜，對算法要求也較高。此外，三維激波相交等問題缺乏理論指導，使得裝配方法在復雜問題中的應用難度較大。諸多問題的存在使得針對三維問題的裝配方法應用研究還較少，目前只是在文獻[30]中看到了相關報道。Bonfiglioli等[30]應用其發展的激波裝配方法研究了一些超聲速流動問題，證實了其方法在解決三維問題中的有效性。盡管如此，從文獻給出的例子還是可以看出，裝配的激波相對較為簡單，流場內激波都是相互獨立的，規避了三維激波相交帶來的問題。本文基于前期關于嵌入式激波裝配方法的研究工作，進一步從二維拓展應用到對三維問題的模擬中。與Bonfiglioli等[30]給出的三維裝配不同，本文在對三維激波問題進行裝配時，不只是針對獨立激波，還考慮了更為復雜并且具有代表性的三維激波相交、反射等問題，結合給出的激波交點的計算方法，完成了對三類超聲速/高超聲速三維激波問題的裝配。

1 三維激波裝配方法

激波裝配方法由2個要素組成：計算和追蹤。所謂的“追蹤”指的是對流場中出現各類間斷位置進行追蹤。所謂的“計算”指的是對間斷邊界包絡計算域內流動利用CFD求解器對偏微分控制方程進行求解的過程。

無論使用什么樣的CFD求解器，在非結構網格范圍內裝配激波是由一系列激波面所表示，這些激波面是由激波點自動連接而成。裝配間斷的位置是通過在激波點上求解R-H關系式獲得。

根據求解器是格心型或者格點型的不同，追蹤激波的方式也會有很大的差異，需要相應地去修改CFD求解器。本文的激波裝配方使用的是格心型有限體積求解器。追蹤激波時，在激波點上求解R-H關系式，以此來獲得激波運動速度。通過激波面元的通量則是使用上游參數以及激波速度得到。一旦獲得通過激波面元的通量，包含激波面元的單元參數的更新方式就和其他單元一樣了。裝配的激波按照求解的激波點速度在拉格朗日體系下移動。采用三維非結構激波裝配方法進行數值分析的過程涉及4個主要內容，下面分別進行詳細介紹。

1) 激波間斷標識

激波裝配方法不像激波捕捉方法那樣對全場采用同樣的處理方式，而是將激波間斷單獨標識出來，用一種解析的有別于光滑區域的方法進行求解。傳統上的邊界激波裝配方法是將激波看作一種特殊的邊界進行標識和計算的。這種方法需要將計算區域劃分成若干個子區域，對于含有懸空激波以及拓撲結構變化的問題不易操作。本文中使用的激波裝配方法是通過節點屬性定義來對激波進行標識的。

如圖1所示，采用網格生成程序(Tetgen)或軟件(Pointwise)生成空間四面體網格。對離散后的網格節點進行屬性定義，劃分為激波節點(Shock nodes, S)和普通網格節點(Common nodes, C)2種。激波面元是由激波節點連接構成的，規定如果一個網格面元包含的節點全部為激波節點則該面元為激波面元。在計算過程中可以根據流場變化對網格節點屬性進行調整，這就極大地提高了激波裝配的靈活性。

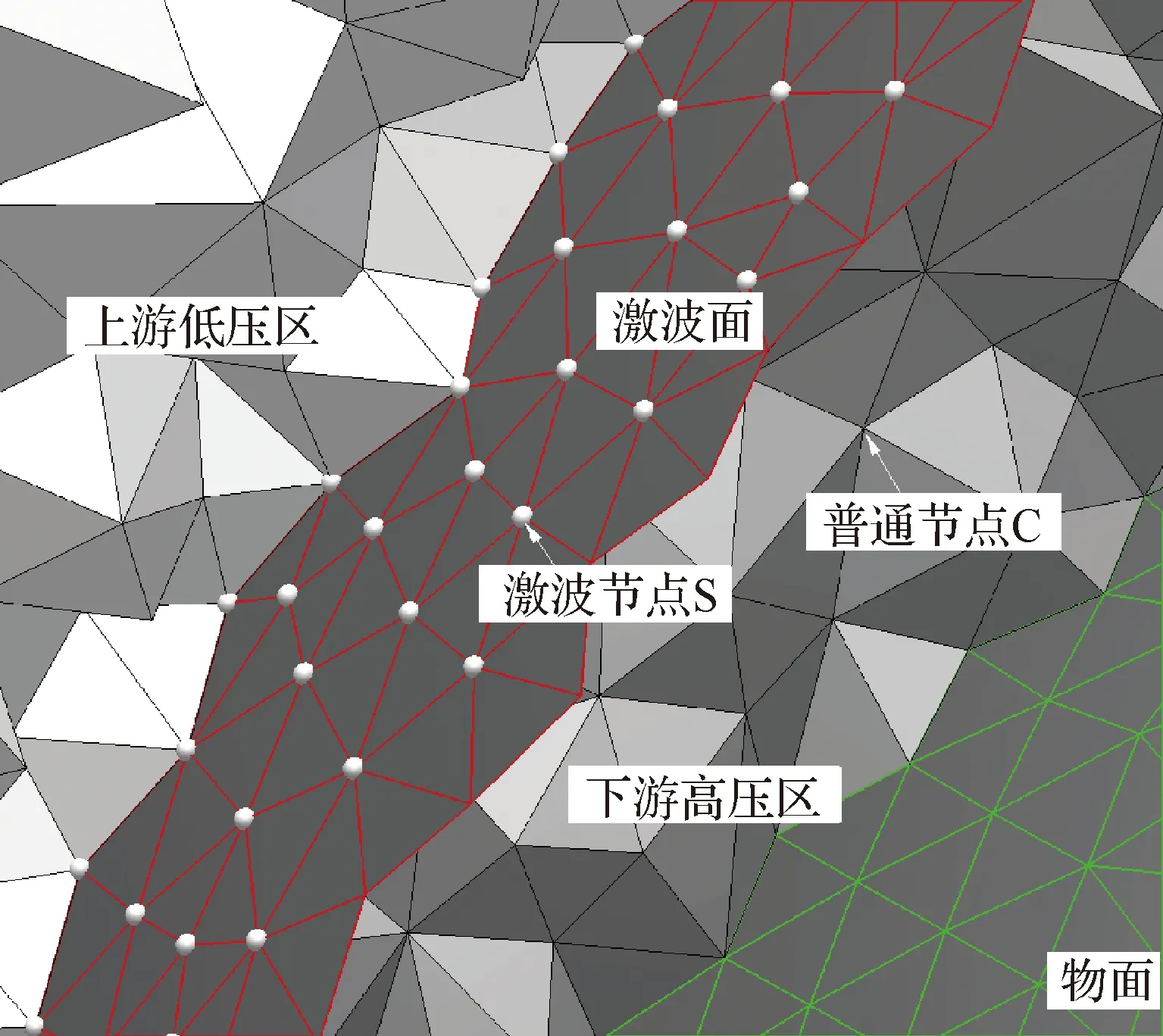
圖1 激波節點標識Fig.1 Labels of shock nodes

2) 網格節點參數確定

采用格心型有限體積方法時，流場參數是儲存在單元格心的。網格節點參數V=[ρ,ux,uy,uz,p]T需要利用格心的流場參數U=[ρ,ux,uy,uz,p]T通過重構獲得。其中，ρ、p分別表示流場密度和壓力；ux、uy、uz為對應于3個方向的流動速度。按照步驟1)中的分類，對于激波節點和普通節點2種節點類型需要2種不同的計算方法。

普通網格節點上的參數主要通過格心參數加權平均得到

(1)

式中：Vi表示節點i上流場參數；N為與網格節點i相鄰的單元數；αik和Uik分別為與之相鄰的第k個單元影響的權系數和格心參數。αik采用節點與單元距離|Rik|的反比進行確定：

(2)

式中：xi和xk為節點i和與之相鄰的第k個單元的格心坐標;Rik為第k個單元與節點i的距離矢量。

基于單元格心參數，利用式(1)、式(2)確定節點參數的方式可以看出，對于普通節點而言，其影響域包含了四周全部的單元。

使用裝配方法對激波間斷處理時需要用到上下游的兩組參數。這個特點決定了被標識的激波節點與普通節點的一個重要區別：包含2組參數，一組代表上游低壓區的影響，一組代表下游高壓區的影響，如圖2所示。對應于上下游，確定其激波節點2組參數所使用的網格單元或影響域和普通節點有所不同，上游節點參數Vu只使用上游低壓區單元，下游節點參數Vd只使用下游高壓區單元

(3)

式中：下標“u”“d”分別表示激波上下游；N1、N2為以激波面為分界包含激波節點的上下游單元個數。與式(1)中N不同的是，在求解式(3)時并非將所有與激波節點相鄰的單元都納入考慮范圍，而是要求影響單元需要包含激波面元。此外，加權系數αik的確定也有所不同，采用式(4)確定:

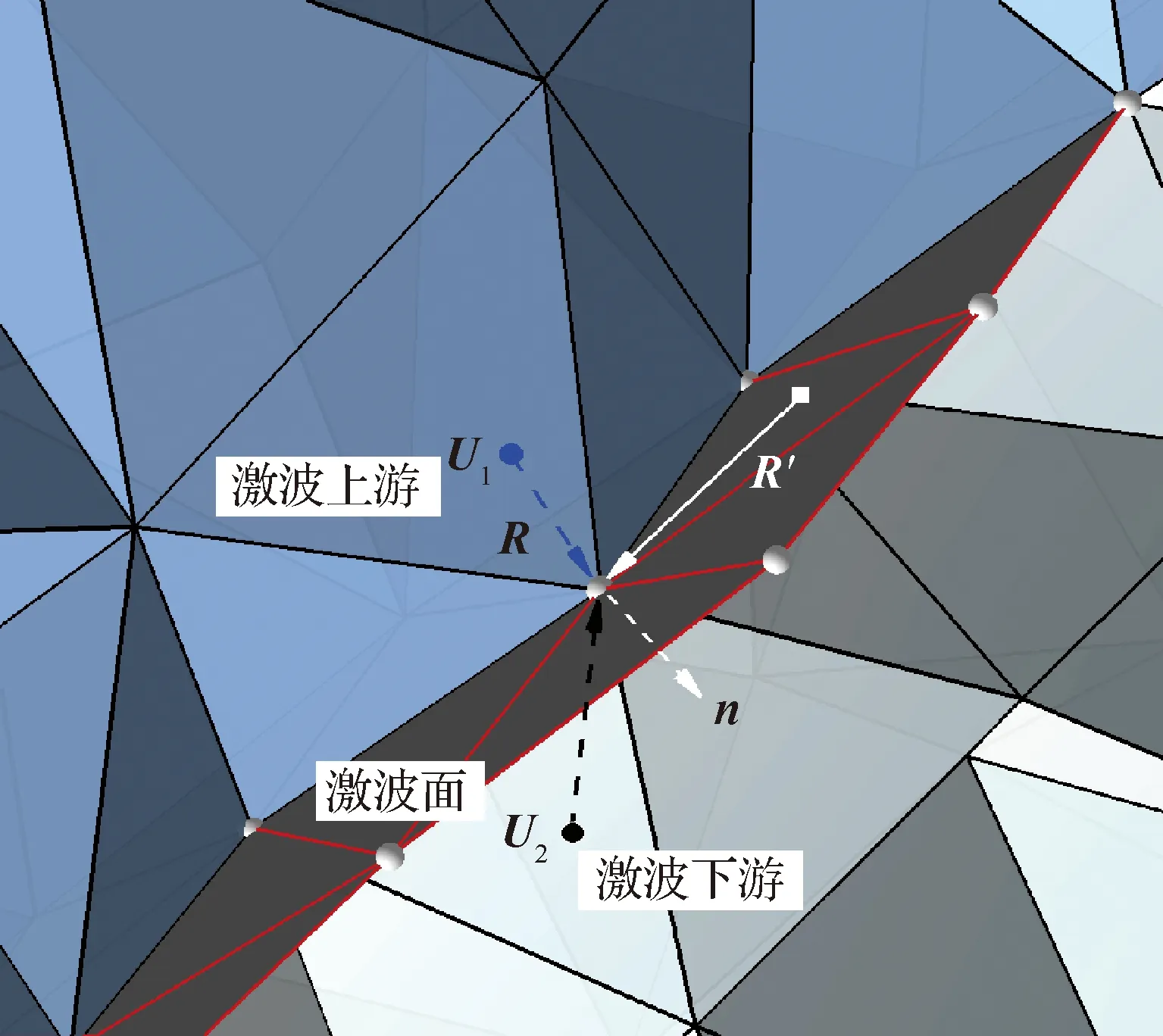
圖2 激波節點參數確定Fig.2 Determination of states on shock nodes

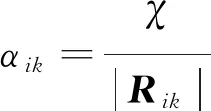
(4)

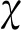
(5)

式中：mτk為第k個單元沿所包含激波面切向的馬赫數，即

(6)

式中：定義u=[ux,uy,uz]T為流場速度矢量，則uk為第k單元的格心流動速度；xc為其所包含的激波面元運動速度；R′為對應激波面元中心到激波節點的空間位置矢量；定義a為聲速，則ak為單元k個單元的格心聲速。

利用光滑區域內單元格心參數確定激波節點上下游參數的過程建立了解析解和數值解之間的聯系。對于激波間斷而言，利用激波節點上下游參數通過求解R-H關系式可以得到激波節點的運動速度。由于R-H關系式是一維的，所以三維激波裝配還涉及到三維問題和一維方程之間的匹配問題。通過建立基于激波節點法向的激波坐標系，可以將三維問題降為一維進行求解。

第i個激波節點法向ni是通過與之相鄰的激波面元法向確定：

(7)

式中：Ns為與激波節點i相鄰的激波面元的個數；nj為第j個激波面元的法向，并且定義激波方向由上游指向下游為正，加權系數α′ij的確定與式(4)類似：

(8)

式中：|R′ij|表示第j個激波面元中心到激波節點i之間的距離大小。

設定激波節點運動速度大小為w，方向為n。在激波坐標系下，激波節點上游流動的相對馬赫數為

(9)

根據上游相對馬赫數，利用R-H關系式并補充反向傳播黎曼變量保持不變的條件可以確定下游參數修正值V′d以及激波運動速度

(10)

式中:前4式為補充了切向速度不變條件的R-H關系式，第5式是根據反向傳播黎曼變量保持不變條件給出，γ表示比熱比。求解上述非線性方程組可以得到激波節點運動速度w以及下游參數修正值V′d。一般情況下，V′d與Vd不相同，修正值V′d主要用于下游單元格心梯度的求解。

3) 激波動態跟蹤

本文使用基于彈簧模型的非結構動網格技術實現對激波的顯式跟蹤。根據式(10)求解的激波節點速度w以及運動方向n，根據t時刻激波激波節點位置xt計算t+1時刻的激波節點位置

xt+1=xt+wnΔt

(11)

式中：Δt為時間步長。根據激波節點位移，利用動網格技術移動其他可移動的網格節點，以保證激波運動變形過程中計算網格的質量。圖3給出了從初始時刻到收斂時刻激波面的運動示意圖。運動過程中，網格質量較差時還需要配合網格重構的策略。

(4) 激波通量計算

采用格心型有限體積求解器對控制方程進行求解時需要計算流經單元面元的通量值。對于普通面元，可以采用各種成熟的迎風格式或中心差分格式進行計算。而對于激波面元來說，通量計算反而變得更加簡單和清晰。在激波坐標系下，激波面元上游為超聲速流動，按照超聲速流動特征，面元通量Φ只和上游流動有關，因此可以根據式(12)進行確定：

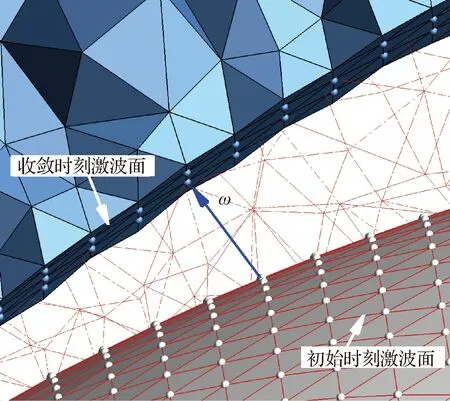
圖3 激波節點運動示意圖Fig.3 Sketch of shock node motion

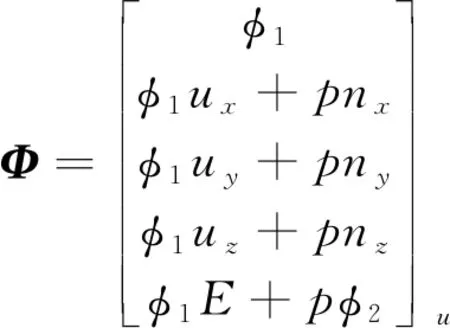
(12)

式中：φ1=ρ(u-xc)·n，φ2=xc·n，E=0.5·u·u+p/[ρ(γ-1)]。n=[nx,ny,nz]T為激波面元法向，激波面元運動速度xc可以根據激波節點運動速度wi和法向ni得到

(13)

式中：N為三維激波面元所包含的激波節點個數。

2 格心型有限體積方法

三維Euler方程的積分形式可以寫為

(14)

式中：Q為守恒變量；Fc(Q)為無粘對流通量；Ω和?Ω分別為控制體單元及其外邊界。

在選定的控制體上，將式(14)中的對流項進行離散可以得到

(15)

式中：Fck、nk、Sk分別為控制單元的第k個表面邊界的通量、外法向單位矢量和面積；Nf為控制體的表面個數。

采用格心型有限體積方法求解上述方程的過程涉及到空間物理量的重構。空間二階格式通常假設物理量在控制單元內為線性分布，即控制單元內梯度為常數。控制單元表面物理量采用不同單元格心值重構得到的結果在表面邊界處形成間斷，采用van Leer等格式進行通量計算，可以獲得通過單元表面的對流通量值，對各個控制單元邊界遍歷求和從而獲得單元內參數變化量。然后對時間導數項進行離散，就可獲得下一時間步的格心處流動參數。關于求解器的詳細介紹可以參考文獻[31]，在此不再贅述。

3 三維算例驗證

3.1 三維弓形激波

高超聲速球柱體繞流是考核計算方法對強間斷問題計算能力的一個重要算例。本文首先使用三維激波裝配方法對來流馬赫數10條件下的該問題進行分析。球柱模型設計如圖4所示，球頭半徑為L，柱體與圓柱相接，長度也為L。計算域選為6L×3L×6L的平行六面體。

不考慮攻角和側滑角情況下，球頭繞流為軸對稱的，流動結構相對簡單，有很多文獻和數據可以用來對本文計算結果進行考核。

根據研究內容需要，設計了3套用于球柱體計算的網格，分別為細網格C-1、粗網格F-1和細網格F-2，網格節點和單元數如表1所示。細網格C-1使用均勻劃分的方式，首先對物面和計算域外邊界使用三角形進行離散，控制參數設為Δ=0.05L，根據邊界網格生成內部計算網格，計算域內全部采用四面體進行劃分。細網格C-1用于激波捕捉方法的計算。為了對激波點進行標記定義，在激波裝配計算網格F-1和F-2中預先設置一個空間面，對該面進行離散后作為內部邊界控制區域網格生成，并在計算中將面上的節點定義為激波點。采用與C-1同樣的網格生成方式，生成粗網格F-1和細網格F-2。其中，粗網格F-1中物面和激波面上的網格離散控制參數設為Δ=0.1L，外邊界控制參數設為Δ=0.3L；細網格F-2中對物面以及激波層內進行加密，網格離散控制參數設為Δ=0.05L，外邊界控制參數同樣設為Δ=0.3L。用于激波捕捉計算的網格C-1在計算過程中不發生網格變形，而網格F-1和F-2會隨著激波的收斂過程發生變形重構。下面對使用3套網格和2種方法生成的計算結果進行對比分析。

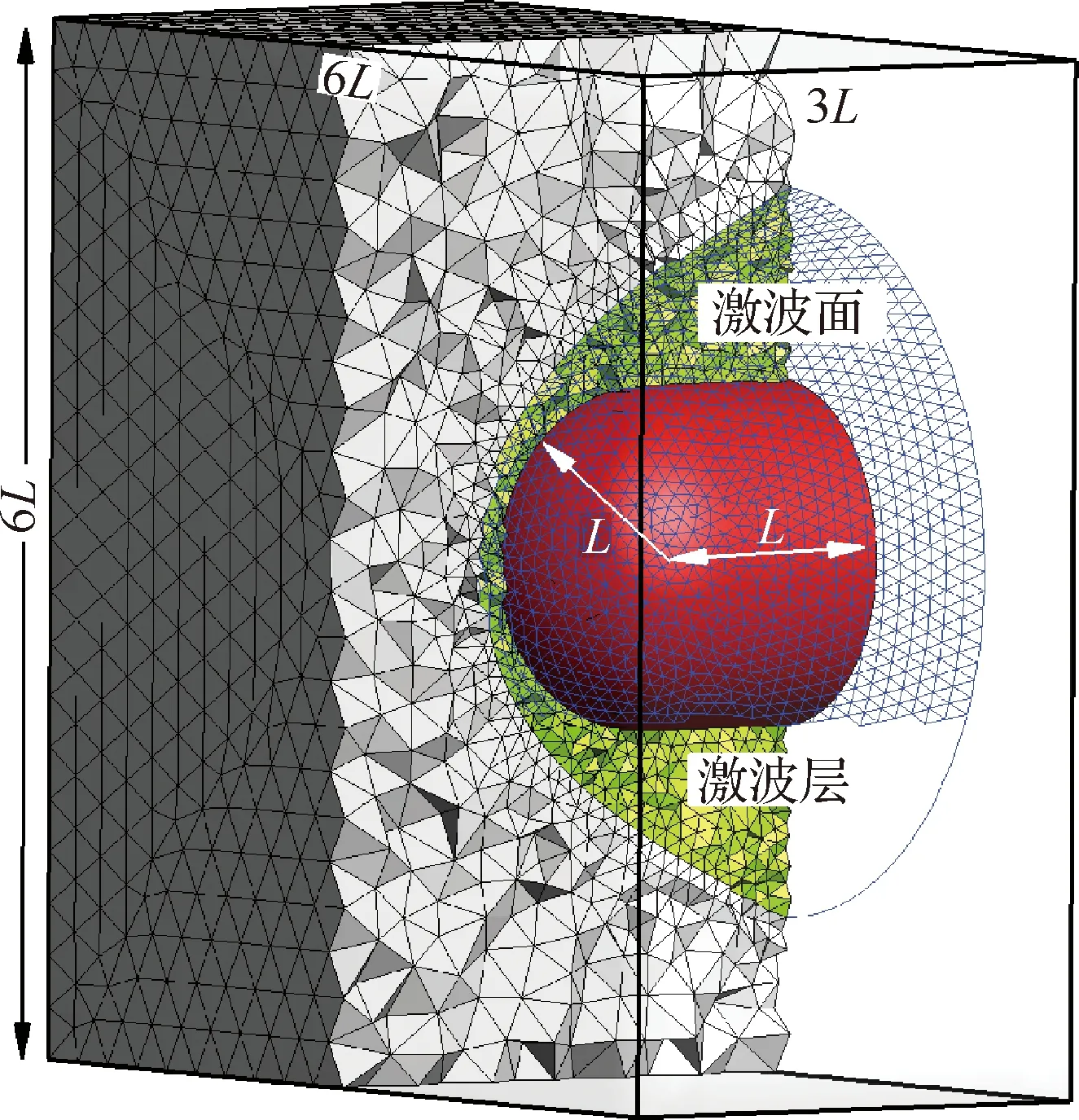
圖4 球柱體: 計算區域及網格Fig.4 Hemisphere-cylinder: computational domain and mesh

1) 激波捕捉和激波裝配對比

本文對激波裝配和激波捕捉2種結果對比時都是采用同樣的求解器和同樣的輸入參數進行計算，不同之處在于激波裝配方法中存在激波節點的定義，網格允許運動。

圖5給出了對稱面上的壓力分布的計算結果。其中上側為采用裝配方法得到的結果，下側為采用捕捉方法計算的結果，黑色線條為文獻[30]中給出的壓力分布。從對比結果可以明顯看出，采用裝配方法得到的結果和文獻符合得非常好，壓力分布完全一致；而采用捕捉方法的計算結果存在一個較厚的激波帶，激波帶對激波層內壓力分布存一定影響，得到的壓力分布明顯前移。進一步，圖6中對比了2種方法計算結果在物面上的壓力分布。從對比可以明顯看出，激波捕捉方法計算結果存在壓力分布前移的現象，對應位置壓力略低于激波裝配的結果。此外，使用激波捕捉得到的壓力分布較不規則，這主要是由于采用非結構網格離散時激波和網格面的斜交程度不同導致環向存在偏差。

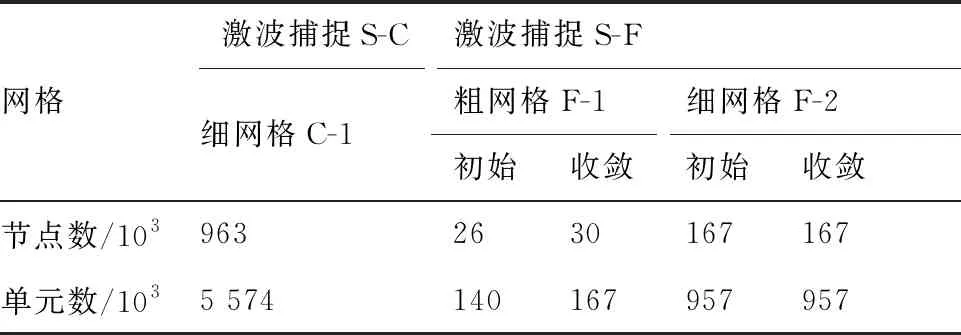
表1 球柱體計算網格Table 1 Computational meshes for hemisphere-cylinder

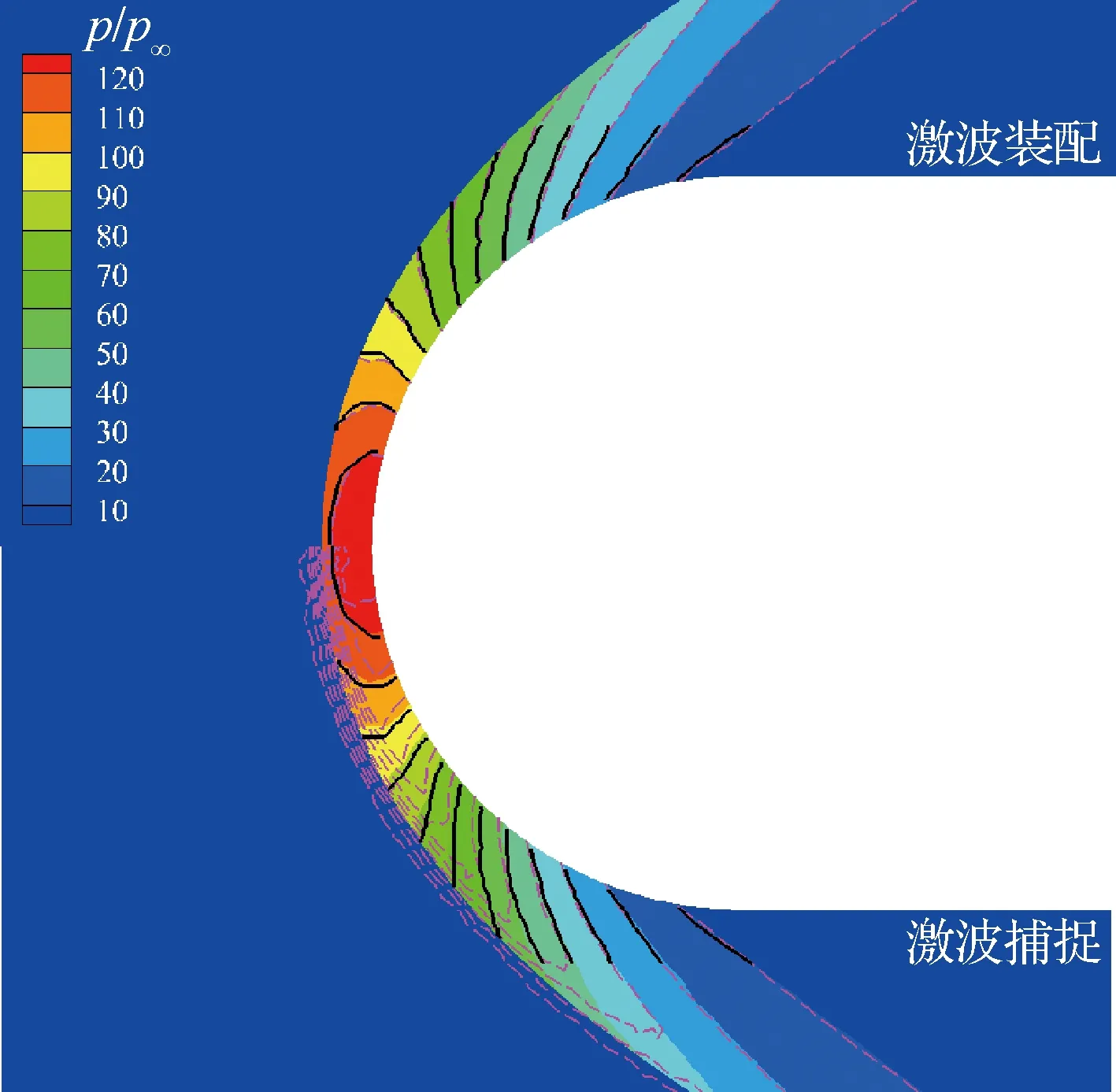
圖5 無量綱壓力等值線云圖Fig.5 Normalized pressure iso-contour levels

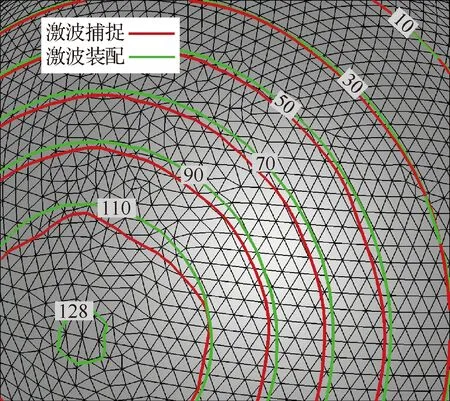
圖6 球頭表面的壓力等值線圖Fig.6 Pressure iso-contour levels on body

2) 激波裝配中粗細網格結果對比

使用激波裝配方法分別基于網格F-1和F-2進行了計算。圖7給出了對稱面上馬赫數計算結果的對比。為了更加直觀地顯示F-1和F-2空間網格的分布情況，圖7還給出了相應的背景網格，上側為粗網格F-1，下側為細網格F-2。可以看出，在激波層內細網格F-2要比粗網格F-1密得多，但基于2套網格得到的激波位置完全吻合，馬赫數分布無較大差異，特別是在球頭區域。對于馬赫數大于2區域內計算結果的偏差主要是由于粗細網格對于膨脹波波系結構的描述以及流場顯示時參數擬合的控制點存在差異造成的。

圖7 激波裝配馬赫數等值線圖Fig.7 Mach iso-contours for shock-fitting

對比網格F-1和F-2的結果可以得出結論，激波裝配方法計算結果對網格粗細并不敏感，使用較少網格量同樣可以獲得足夠高質量的計算結果。從這點來看，使用激波裝配方法模擬時可以適當減少網格量，從而提高計算效率。

3.2 三維激波反射

球柱體繞流只包含一個弓形激波，裝配難度相對較低。進一步，我們考慮一個較為復雜的包括一個正規反射的管內激波反射問題。設計模型如圖8所示，在圓型通道內放置一個圓錐模型，以圓筒直徑L為參考，圓筒半徑為R=0.5L。圓錐模型底部到理論尖點的長度為L，圓錐半錐角δ=10°。為了更加貼近實際飛行器模型，圓錐頭部選為球形，半徑為0.02L。

考慮圓筒內來流馬赫數Ma∞=2。超聲速氣流遇圓錐產生脫體圓錐激波，圓錐激波遇筒壁影響會發生反射。由于流動具有軸對稱的特點，所以計算區域只選擇1/4，即圖8中實線框內區域。計算區域采用四面體單元進行離散，四面體單元數約為35萬。

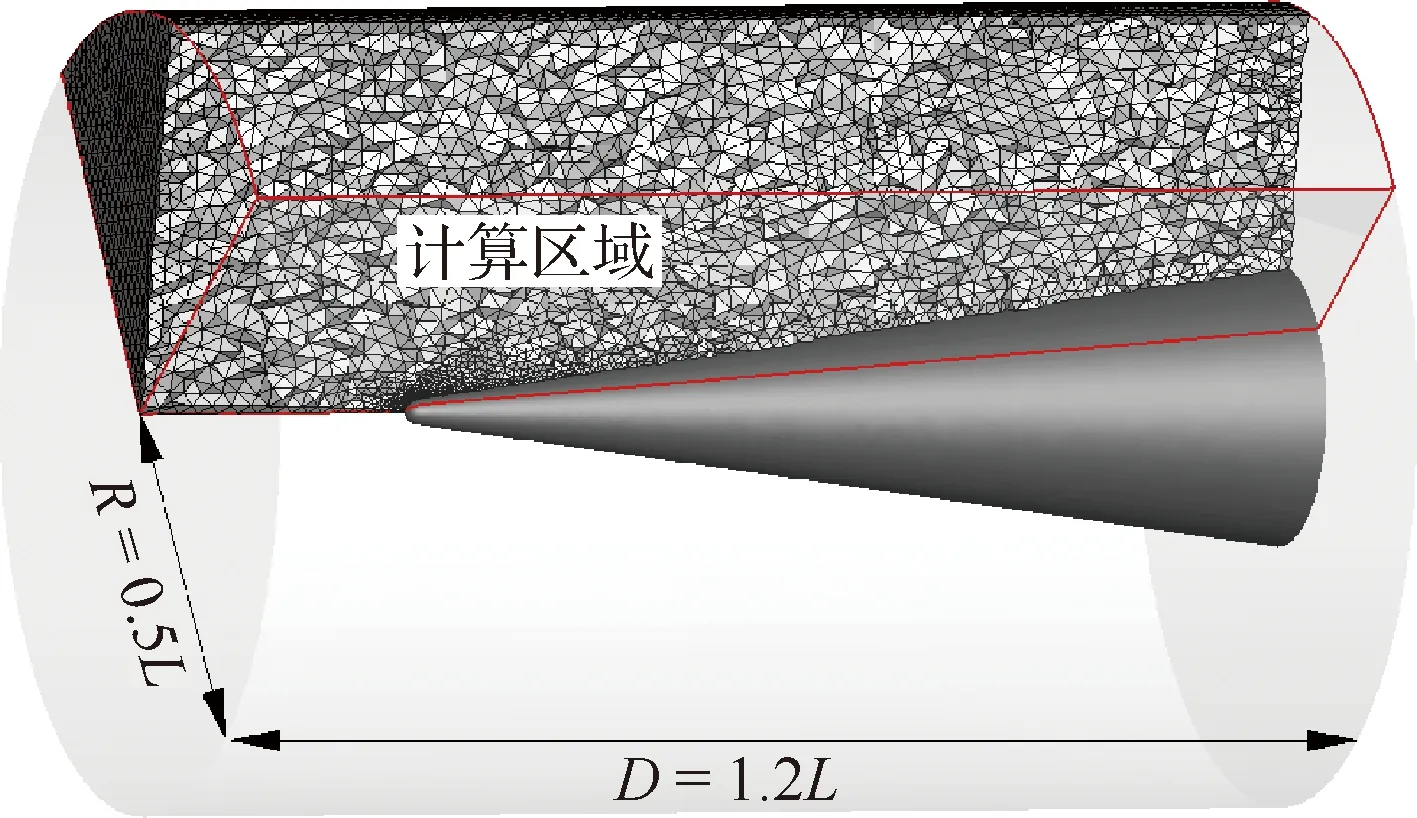
圖8 激波反射：計算域和網格Fig.8 Shock reflection: computational domain and mesh

采用三維激波裝配方法對入射激波和反射激波進行裝配。由于激波在壁面發生反射，涉及到激波壁面交點運動參數的確定。三維激波交點運動參數的確定要比二維復雜得多，其運動速度求解不當會出現不相容問題，導致計算失敗。所以激波交點運動參數的確定對于三維裝配而言至關重要。

根據正規反射的特點，從幾何構型的角度出發認為激波在筒壁上反射點的運動速度主要受入射激波影響，應與入射激波相匹配，即與壁面交點的運動速度wR應由入射激波決定，可以利用式(16)進行確定：

wR=(wI·τw)τw

(16)

式中：wI為按照入射激波確定交點參數得到的激波節點速度;τw為壁面的切向向量。

裝配方法得到的激波型面如圖9所示。為了更加直觀地顯示激波面形狀將計算結果進行對稱，可以看出激波面光滑合理，定性說明裝配的正確性。對計算結果進行一步分析，給出了裝配激波的角度。根據氣體動力學相關知識可知，超聲速軸對稱繞流形成的附體圓錐激波從每個子午面來看都是斜激波。在馬赫數Ma∞=2、半錐角δ=10°條件下，激波角β=31.2°。從圖9的對比可以看出，由于圓錐頭部為球形，激波會脫體，對下游流動造成影響。隨著距離增加，激波角減小，最后收斂至錐形流理論激波角31.2°。入射激波壁面反射為正規反射，反射激波角度可以根據入射激波角31.2°和來流馬赫數Ma∞=2進行確定。經計算反射激波角為β′=30.6°，與裝配激波角度吻合較好。值得說明的是，遠離洞壁時反射激波上游并非勻直流，反射激波角度會出現一定偏差。

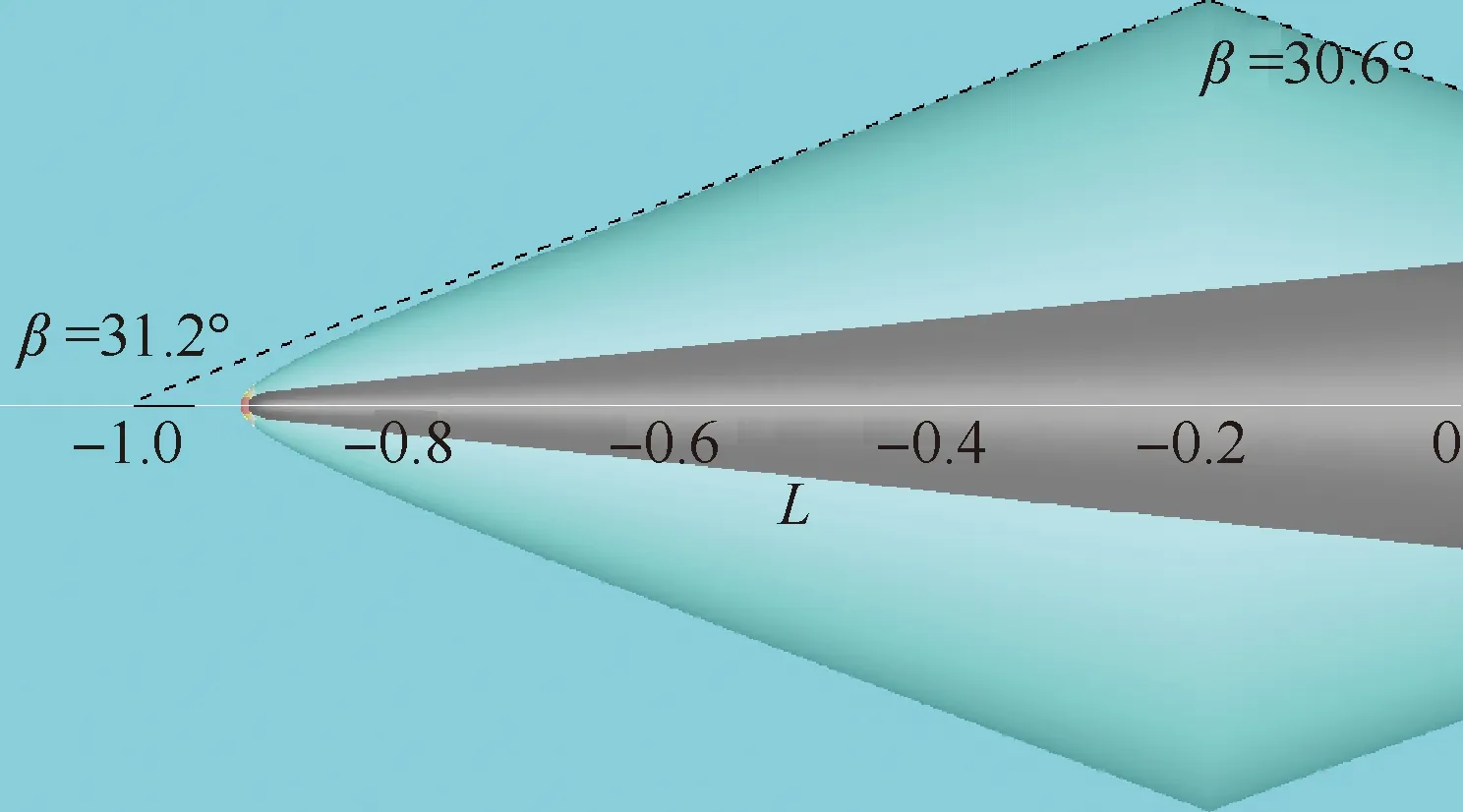
圖9 激波反射：裝配得到的激波Fig.9 Shock reflection: fitted shock waves

3.3 三維激波-激波相交

最后考慮一個更為復雜的含有激波相交的流動問題—球柱錐組合體超聲速繞流問題。針對該問題Houtmann[32]、Bonfiglioli[30]分別進行了實驗和數值研究。選用他們研究的模型和參數，如圖10所示，使用三維激波裝配方法進行模擬計算。具體模型尺寸如圖10所示，來流馬赫數Ma∞=4.04，攻角為α=20°。該問題涉及到球頭和拐角處形成的脫體激波和附體激波的裝配以及對兩個激波形成的三維激波相交的裝配，裝配難度較大。

根據流動特點，計算區域選擇如圖11所示。采用完全的四面體網格對計算區域進行離散，離散控制參數設為Δ=2 mm，離散網格量約為94萬，用于激波捕捉方法使用的計算網格。如前所述，使用激波裝配方法計算時為了對激波點進行標記定義，預先設置激波面，通過激波面和邊界對計算區域進行網格劃分，網格量約為110萬。

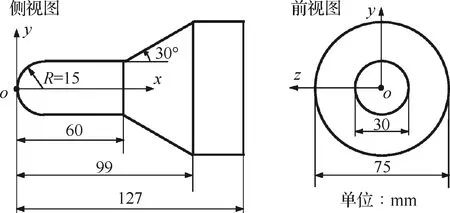
圖10 模型尺寸圖Fig.10 Body geometry and dimension

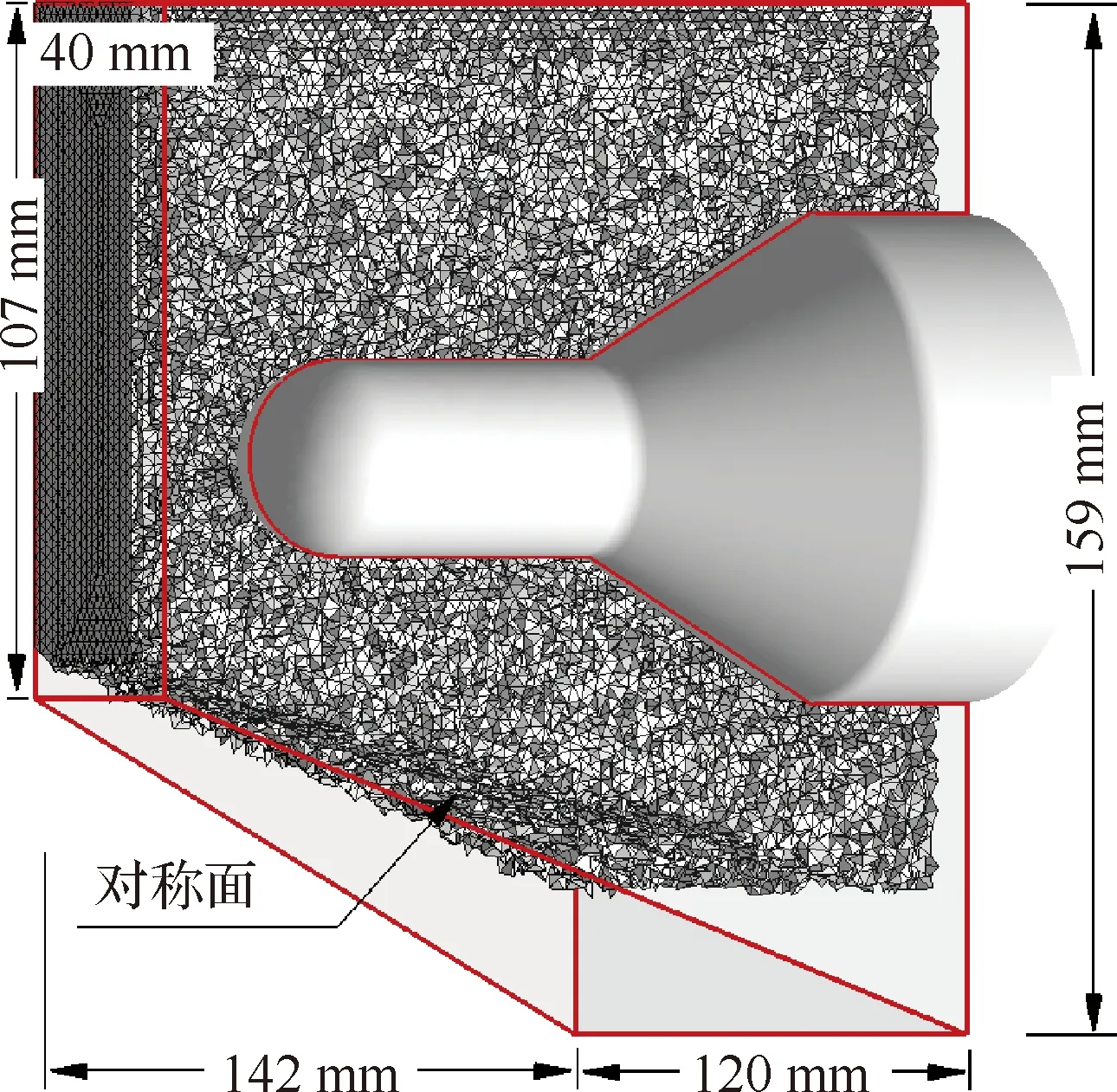
圖11 激波相交：計算域及網格Fig.11 Shock interaction: Computational domain and mesh

在來流條件作用下最外層形成的脫體弓形激波與錐裙和圓柱的結合處形成的內嵌激波相交形成VI類激波相交構型，如圖12所示。如前文所述，對于該問題進行裝配的難點和重點依然是如何確定激波交點運動速度。根據流動特點，本文給出了一種適用于此類三維激波交點運動速度的確定方法。通過對該類型激波結構的特點進行分析可知，激波交點T的運動速度由處于上游的2個激波I1和I2的運動決定。利用此關系，假設I1和I2的激波運動速度分別為w1和w2，運動方向分別為n1和n2，激波交點T的運動速度w可以通過求解式(17)確定：

(17)

式中：n=n1×n2為平面Π的法向向量。

利用式(17)對交點運動進行計算，得到收斂的激波裝配結果，如圖13所示。從結果來看，激波型面光滑合理，根據控制方程解唯一性特點可以在一定程度上反映裝配結果的正確性。利用三維激波裝配方法得到的激波型面使得對三維激波的認識更加直觀。

圖14給出了激波裝配方法和激波捕捉方法在對稱面上的馬赫數云圖對比，從對比結果可以看出：激波裝配和激波捕捉得到的流場結果分布基本一致，也反映了裝配結果的合理性，從而驗證了三維激波裝配方法適用于對復雜激波構型問題的裝配。進一步對比可以看出，捕捉方法得到的激波存在一個較厚的激波帶，隨著激波強度的變弱厚度還有增大的趨勢，而激波裝配得到的激波為理論上的厚度為零。

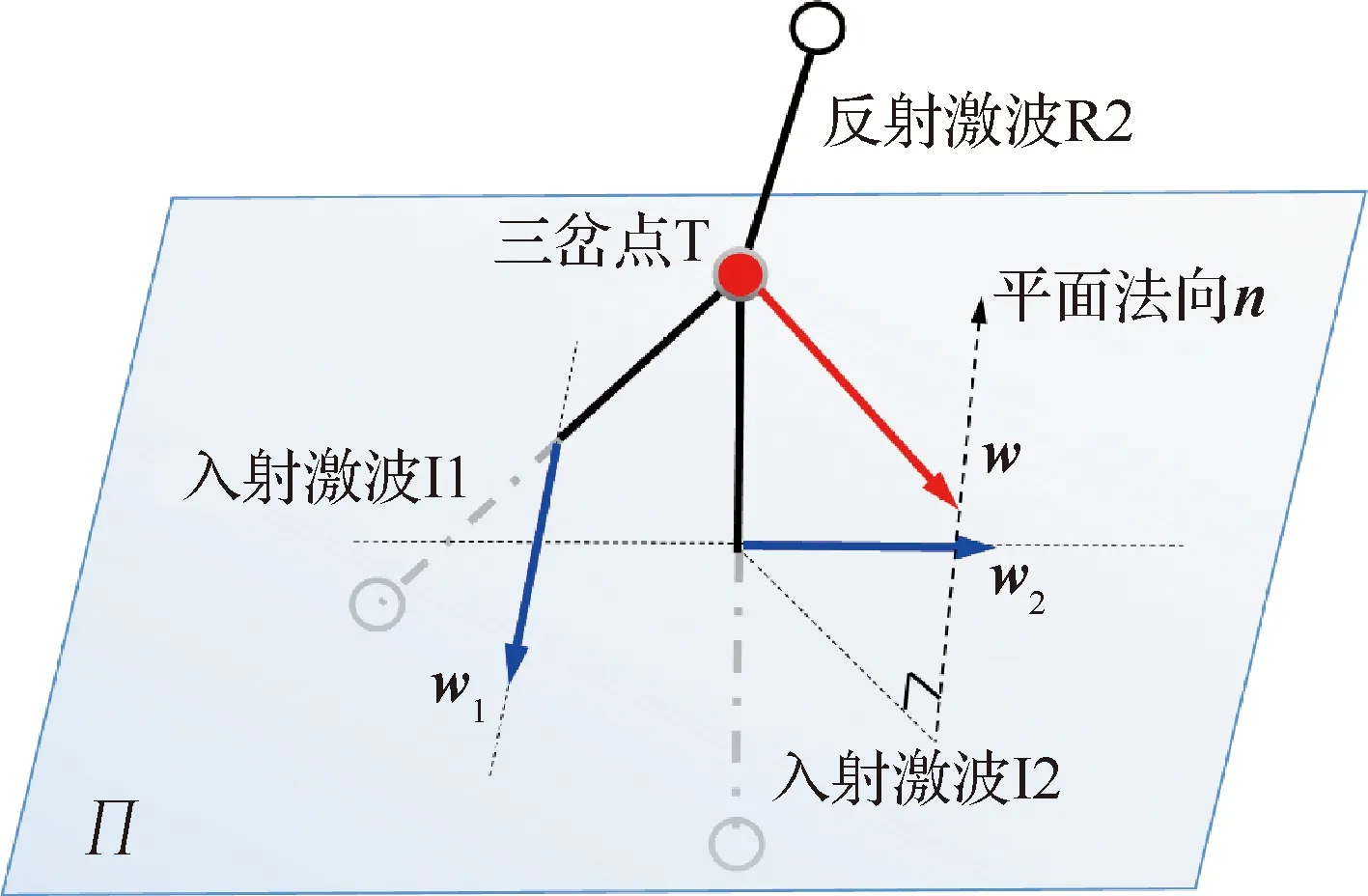
圖12 激波結構示意圖Fig.12 Sketch of shock structure

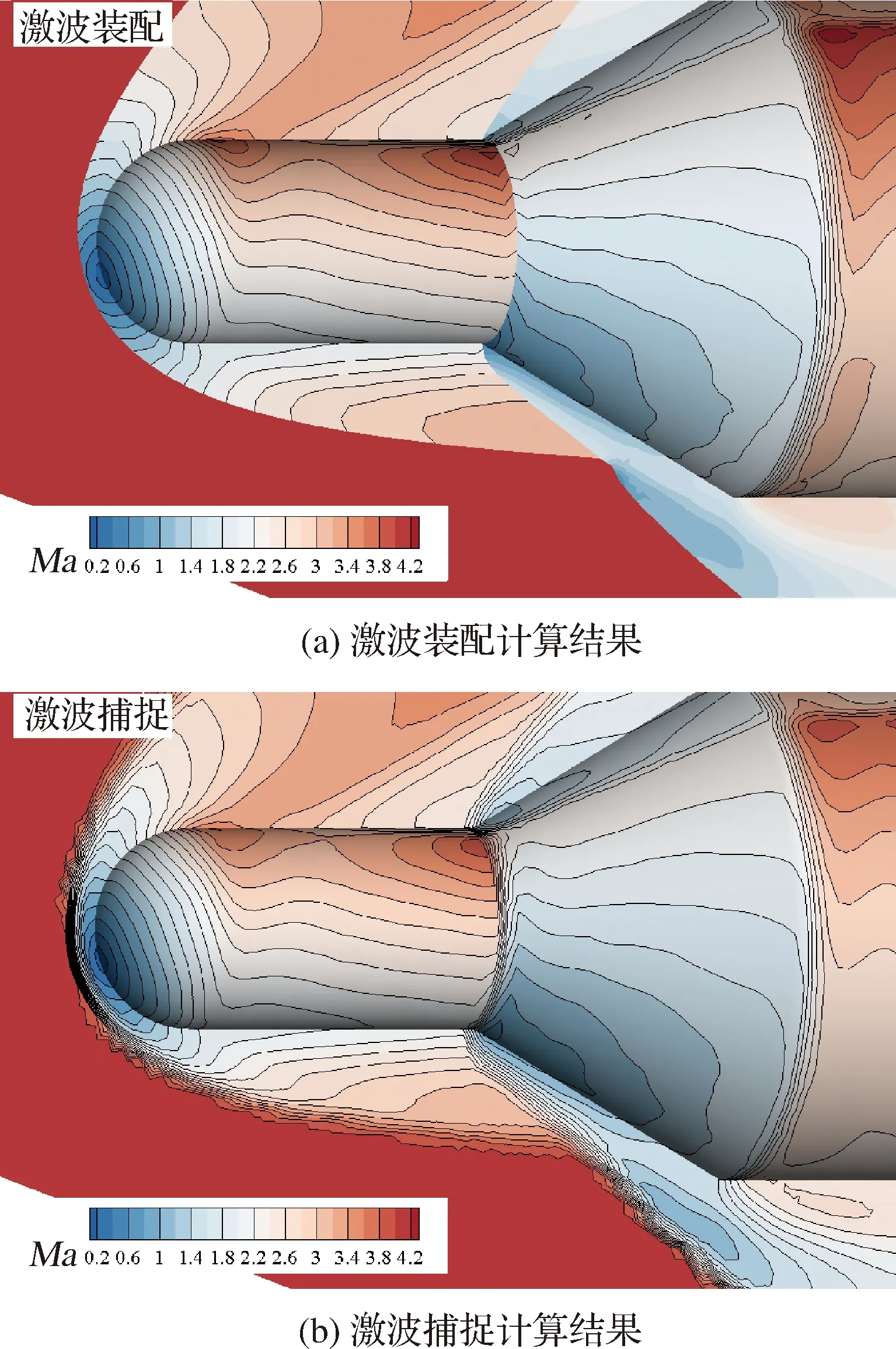
圖14 對稱面上馬赫數云圖Fig.14 Mach number iso-contours on symmetric plane

4 結 論

本文將基于非結構動網格的激波裝配法拓展應用于對三維問題的研究，數值模擬了若干含有不同激波個數以及不同激波結構的超聲速/高超聲速流動問題。計算結果顯示該方法具有適用于三維問題的能力。通過對高超聲速球柱繞流問題的模擬驗證了該裝配方法在三維問題中的合理性。在激波壁面反射和激波相交問題中，通過對激波結構的幾何關系的分析發展了適用于描述這兩類三維激波交點運動的方法。理論上，在其他類型的三維激波相交問題中利用激波構型的幾何特征確定激波交點速度的方法也是適用的。通過本文工作，對傳統裝配方法進行了改進，拓展了裝配方法的應用范圍。三維激波裝配可以獲得合理的激波型面，增加了對三維激波形狀的直觀理解，對于相關理論方法的研究也具有一定參考意義。

激波裝配方法發展的一個重要目的就是解決其通用性問題，實現其在更為復雜的工程問題中的應用價值。針對三維問題進行研究，會發現二維裝配所遇不到的問題，以解決相關問題為導引有利于加速發展出更為通用的激波裝配方法。本文關于三維激波裝配方法的研究正是沿著這一思路而來。但是從目前來看，關于三維激波裝配仍然還有很多工作要做。本文提出的激波交點的計算方法是利用激波結構的幾何關系獲得，背后的物理含義仍然需要作大量的探索研究。對于基于非結構動網格的激波裝配方法，給定的初始激波和收斂時的激波位置距離較遠時，激波運動幅度較大，需要不斷進行網格重構，嚴重影響計算效率。精確的激波辨識可以提供相對準確的激波面，有助于提高計算效率。關于激波面的辨識依然是三維激波問題的一個重點。諸如此類的問題在一定程度上都還制約著激波裝配方法的實際應用，有待后續深入研究。