一種機載PD雷達交互多模型濾波方法

馬 娟，范玉珠，李 樂

(1. 中國電子科技集團公司第三十八研究所，安徽合肥 230088； 2. 中國人民解放軍63629部隊，北京 100162)

0 引言

PD雷達常用于機載預警和火控雷達領域，利用目標與雷達之間的相對運動產生的多普勒效應進行目標信息提取和處理。機載PD雷達具有良好的下視和上視探測能力、精確的多普勒速度量測能力和同時探測數十批甚至上千批目標的能力。雷達數據處理系統對量測數據進行關聯和濾波，形成可靠的雷達情報[1-2]。航跡跟蹤中濾波算法的性能直接影響雷達情報質量。

機載雷達在以載機為中心的運動平臺上獲得量測數據，量測數據直接描述的是雷達和目標的相對位置變化[3]，一般情況下雷達和目標的相對運動狀態方程是非線性方程，很難直接進行濾波和預測。機載PD雷達濾波時一般將量測數據轉換到以地面測量站為中心的慣性坐標系(簡稱地面慣性坐標系)下，再采用與地面雷達相同的處理方法進行濾波。該方法存在以下缺點：目標在某一時刻只能有一種假設的運動模型，如果目標運動狀態與運動模型不匹配，會導致濾波器嚴重發散；量測數據轉換到地面慣性坐標系下進行濾波，用經過非線性變換后的數據濾波，數據的噪聲特性失真，導致濾波器精度下降；作為PD雷達特色的目標多普勒速度在濾波過程中沒有得到利用，損失了一維重要的信息。

目前機動目標跟蹤的主流算法是交互多模型(Interactive Multi-Model，IMM)濾波算法[4-6]。本文方法采用IMM濾波器，模型集由勻速直線運動(CV)模型、當前統計(CS)模型和估計角速度的勻速轉彎運動(CT)模型組成。其中，CV模型和CS模型采用線性卡爾曼濾波實現，CT模型采用容積卡爾曼濾波實現[7]。濾波器量測誤差協方差矩陣由天線坐標系下的量測誤差和天線坐標系下的量測值進行無偏轉換近似計算。利用機載PD雷達多普勒速度量測精度高的特性，將其應用到模型概率初始估計和模型參數初始估計中，提高模型初始參數的精度。

1 基于CV模型、CS模型和CT模型的交互多模型濾波器

基于CV模型、CS模型和CT模型的交互多模型濾波器周期運行，由數據驅動，每一次關聯成功后，濾波器的工作步驟如下：

1) 量測數據預處理

接收到每一個周期的探測數據后進行量測數據的預處理，包括量測誤差協方差矩陣計算和濾波器輸入量測數據計算。

2) 模型初始化

濾波器第一次調用時，初始化模型概率、模型參數和Markova轉移矩陣。

3) 狀態向量和協方差初始化

濾波器第一次調用時，根據先驗信息和已獲得的量測數據初始化各模型的狀態向量和協方差 (j=1,2,3分別對應CS、CV、CT模型，下同)。

4) 相互作用

計算與每一個模型匹配的濾波器的混合初始條件。模型j在k時刻的初始狀態向量為

(1)

相應的協方差為

(2)

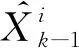
5) 卡爾曼濾波

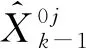
6) 計算模型的可能性

(3)

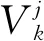
7) 模型概率更新

(4)

(5)

8) 組合估計

狀態向量和協方差的最終組合結果為

(6)

(7)

2 量測數據預處理

濾波器啟動前需要先進行量測數據的預處理，包括量測誤差協方差矩陣計算和濾波器輸入量測數據計算。計算量測誤差協方差矩陣時，先由直接測量得到的目標在天線坐標系下的距離、方位和載機姿態角信息獲取對應的距離量測誤差、方位量測誤差和載機慣性坐標系下的極坐標量測值，再采用無偏轉換方法計算量測誤差協方差矩陣。載機慣性極坐標系下的量測值和對應時刻的載機大地坐標位置進行坐標變換獲得地面慣性坐標系下的位置作為濾波器輸入量測數據[8]。

由式(8)計算目標在天線坐標系下的直角坐標位置P1=[x1,y1,z1]T。其中r1，a1，e1為根據第k個周期雷達探測的目標原始回波解算出的位置坐標，分別表示目標距離(單位：m)、目標方位角(以機頭為中心，單位：rad)和目標俯仰角(單位：rad)。

(8)

根據探測點跡距離r1和方位角a1，由雷達特性和統計分布等先驗信息，獲得距離量測誤差dr和方位量測誤差da。計算量測誤差協方差矩陣為

(9)

其中，

(cosh(2·da2)-cosh(da2))+

(sin(a1))2·(sinh(2·da2)-sinh(da2)))+

dr2·exp(-2·da2)·((cos(a1))2·

(2·cosh(2·da2)-cosh(da2))+

(sin(a1))2·(2·sinh(2·da2)-sinh(da2)))

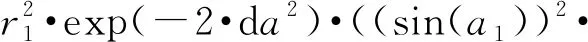
(cosh(2·da2)-cosh(da2))+

(cos(a1))2·(sinh(2·da2)-sinh(da2)))+

dr2·exp(-2·da2)·((sin(a1))2·

(2·cosh(2·da2)-cosh(da2))+

(cos(a1))2·(2·sinh(2·da2)-sinh(da2)))

r12=sin(a1)·cos(a1)·exp(-4·da2)·

r21=r12

由式(10)計算旋轉變換公式T1，其中，α、β、γ分別為載機的偏航角、俯仰角和橫滾角(單位：rad)。

T1=

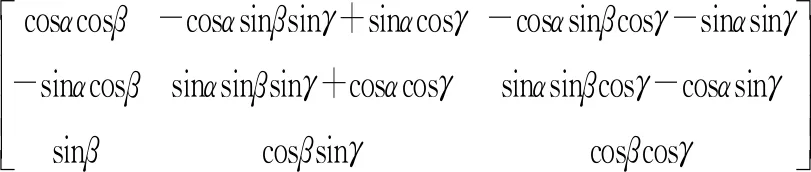
(10)

由式(11)計算目標在載機慣性坐標系下的直角坐標值P2=[x2,y2,z2]T。

P2=T1*P1

(11)

再由式(12)計算目標在載機慣性坐標系下的極坐標值。

(12)

已知P2、載機位置和地面測量站的位置，利用大地坐標變換公式計算目標在測站坐標系下的直角坐標位置Zk=[x,y,z]T，Zk即是第k個周期濾波器的輸入量測值。

3 濾波器實現

3.1 模型的初始概率和參數初始化

交互多模型濾波器中各模型的初始概率和模型參數根據速度、加速度和徑向速度估計，加速度和徑向速度的變化對應目標的機動情況，對一批目標第一次濾波時，根據徑向速度、加速度和目標機動的先驗分布，獲得模型初始概率和初始機動參數。

1) 模型概率初始化

(13)

2) 初始化模型預置參數

由dλ和CS模型機動因子的先驗分布獲得機動因子α的最大后驗估計。CT模型的轉彎角速度w初始化為0。

α=argmaxp(α|dλ)

(14)

3) 初始化Markova轉移矩陣

濾波器第一次調用時，初始化模型組的Mar-kova轉移矩陣P，其中pij(i=1,2,3;j=1,2,3)表示模型i到模型j的轉移概率。轉移矩陣中CV模型與CS模型可相互轉換，CV模型與CT模型可相互轉換，CS模型與CT模型之間不能相互轉換。

(15)

3.2 容積卡爾曼濾波器

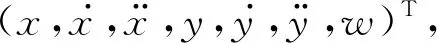
時間更新的計算步驟如下：

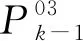
(16)

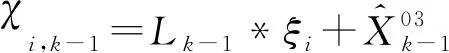
(17)

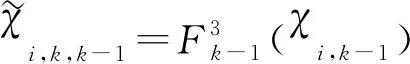
(18)

4) 通過經CT模型狀態方程傳遞后的2n個cubature點的狀態來估計k時刻的狀態

(19)

5) 計算k時刻2n個cubature點的狀態對應的協方差的一步預測

(20)

式中，Qk-1為過程噪聲協方差矩陣。

觀測更新的計算步驟如下：

1) 對協方差的一步預測Pk,k-1進行喬列斯基分解：

Pk,k-1=Lk,k-1*(Lk,k-1)T

(21)

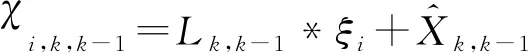
(22)

(23)

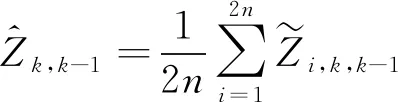
(24)

3) 求k時刻的新息協方差：

(25)

求k時刻狀態預測誤差與量測預測誤差的互協方差矩陣：

(26)

計算容積卡爾曼濾波的濾波器增益:

(27)

計算k時刻的新息：

(28)

進行k時刻的狀態更新：

(29)

進行k時刻的協方差更新：

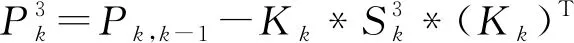
(30)

4 仿真實驗

為了驗證算法的有效性，結合目標仿真系統進行了仿真實驗，實驗結果顯示本文方法明顯提高了濾波精度，對機動和非機動狀態的目標均有穩定的濾波效果。

4.1 實驗一

實驗一采用MATLAB仿真，仿真參數如下：

載機運動軌跡：載機與目標初始距離100 km，載機以100 m/s的速度向正北方向進行勻速直線運動。

目標運動軌跡：目標以200 m/s的速度進行40 s的勻速直線運動，之后以0.1 rad/s的角速度進行60 s的勻速轉彎運動，之后勻速運動30 s，再以-0.1 rad/s的角速度進行60 s勻速轉彎運動，最后勻速運動30 s。

濾波器參數設置：距離量測誤差150 m；方位角量測誤差0.1°；幀周期10 s；蒙特卡洛仿真次數100。

圖1所示為目標真實運動軌跡的采樣值，圖2為觀測值和濾波值的絕對距離誤差的均方根。由圖可見，在目標機動或非機動狀態下，濾波結果都優于觀測結果，濾波器具有良好的自適應性能。

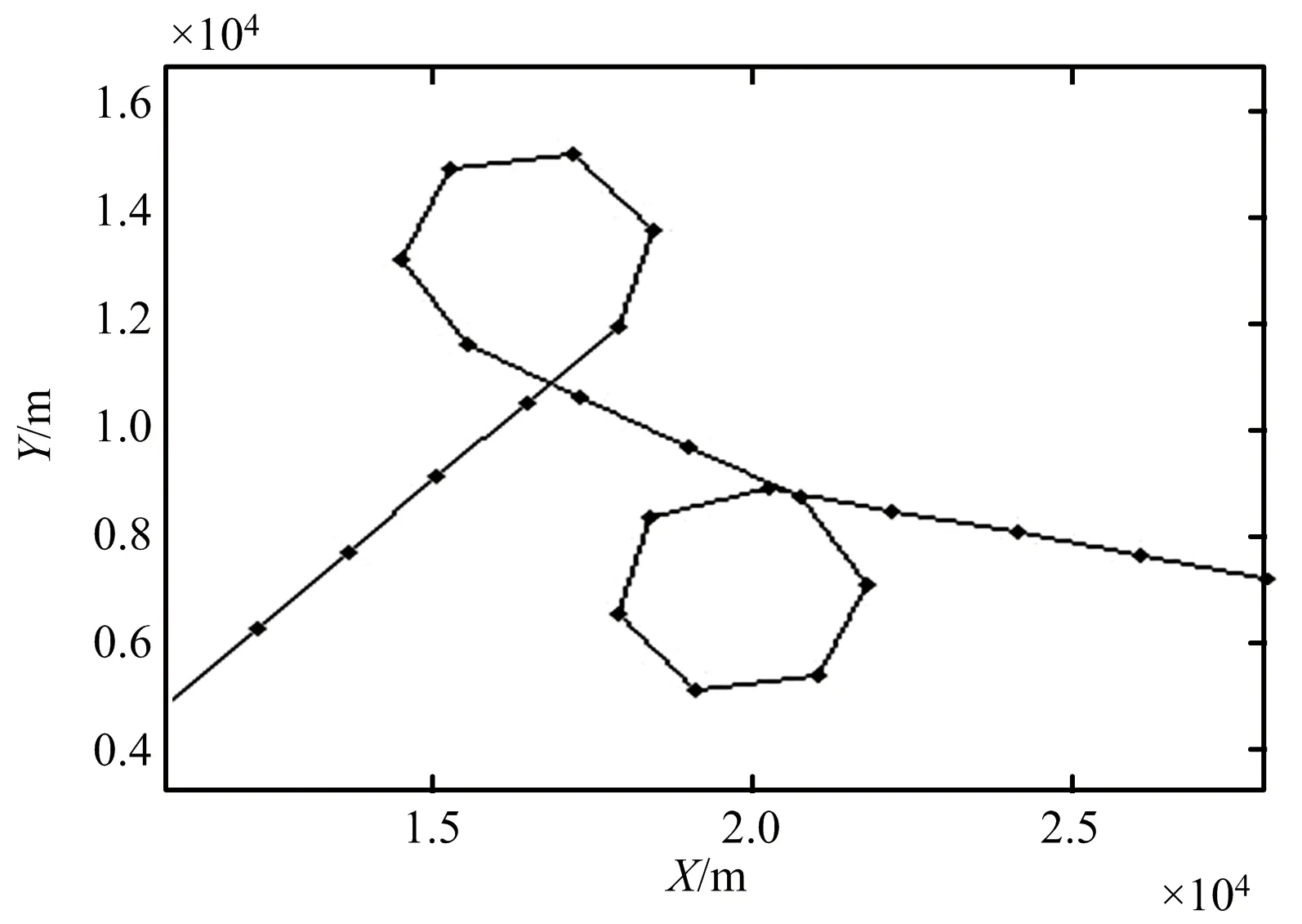
圖1 實驗一目標軌跡

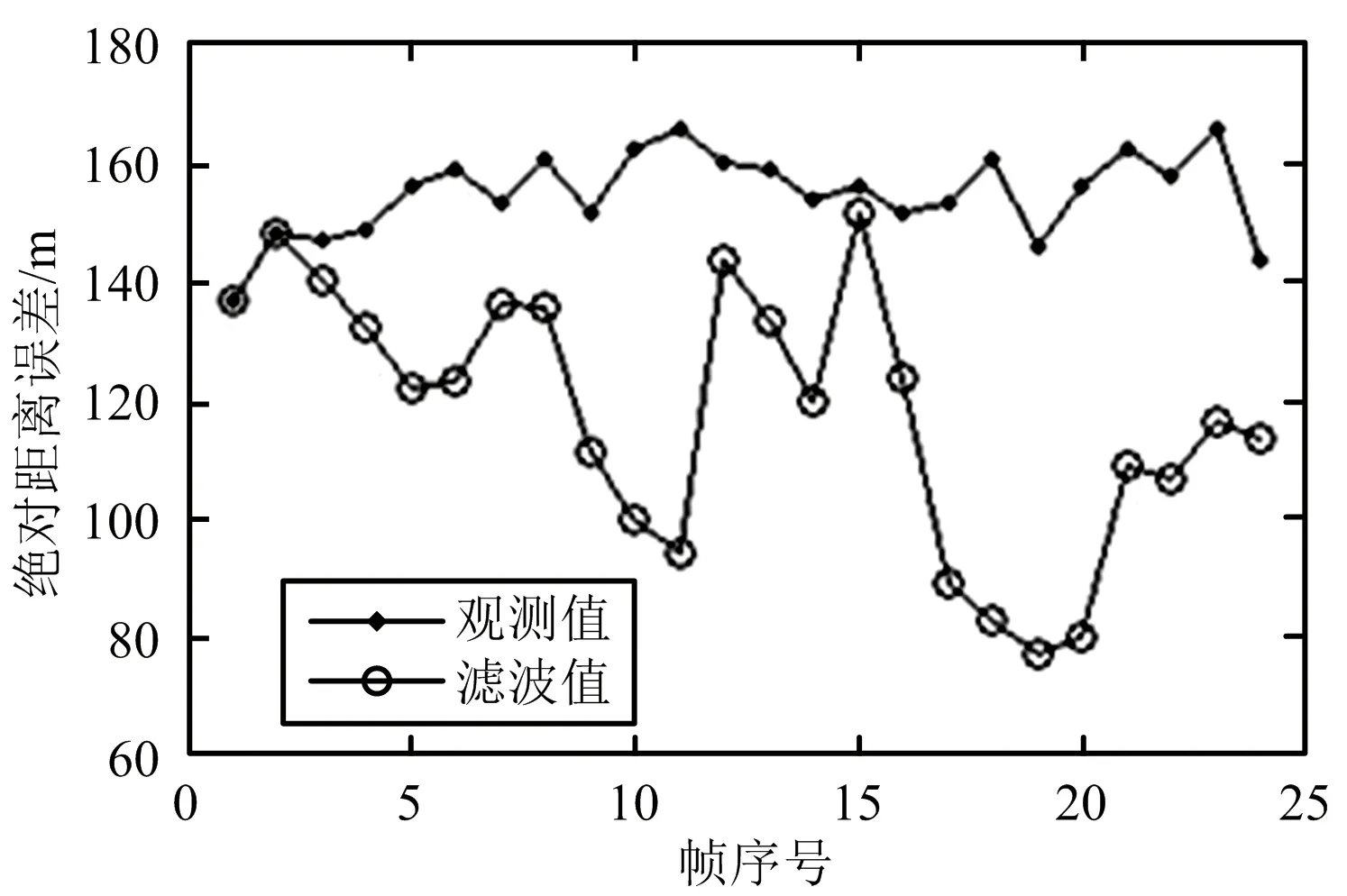
圖2 實驗一目標濾波前后誤差

4.2 實驗二

實驗數據來源于某機載雷達仿真系統，目標進行隨機機動，目標軌跡如圖3所示，濾波前后目標位置的絕對距離均方根誤差如圖4所示。濾波后精度明顯優于測量精度。

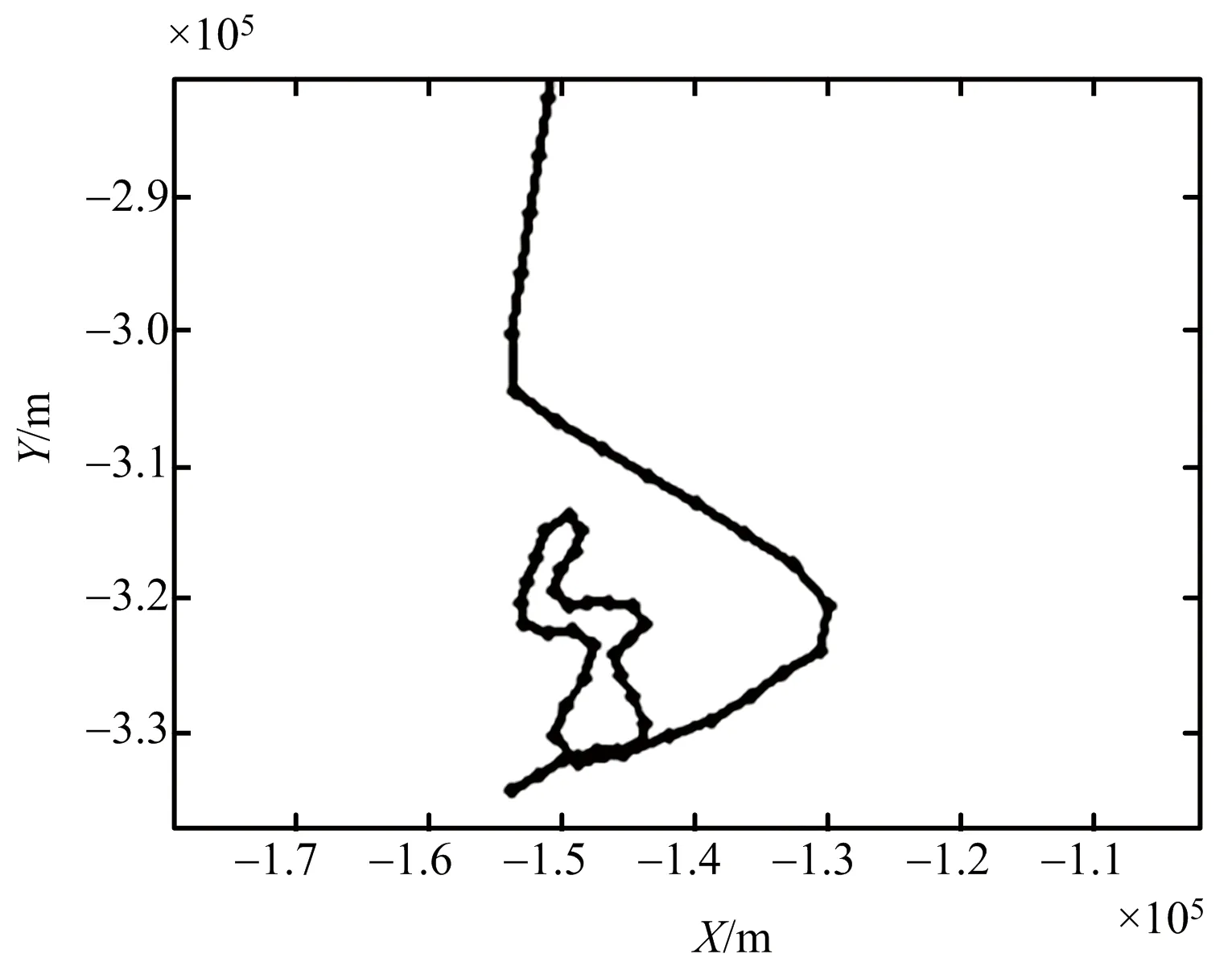
圖3 實驗二目標軌跡

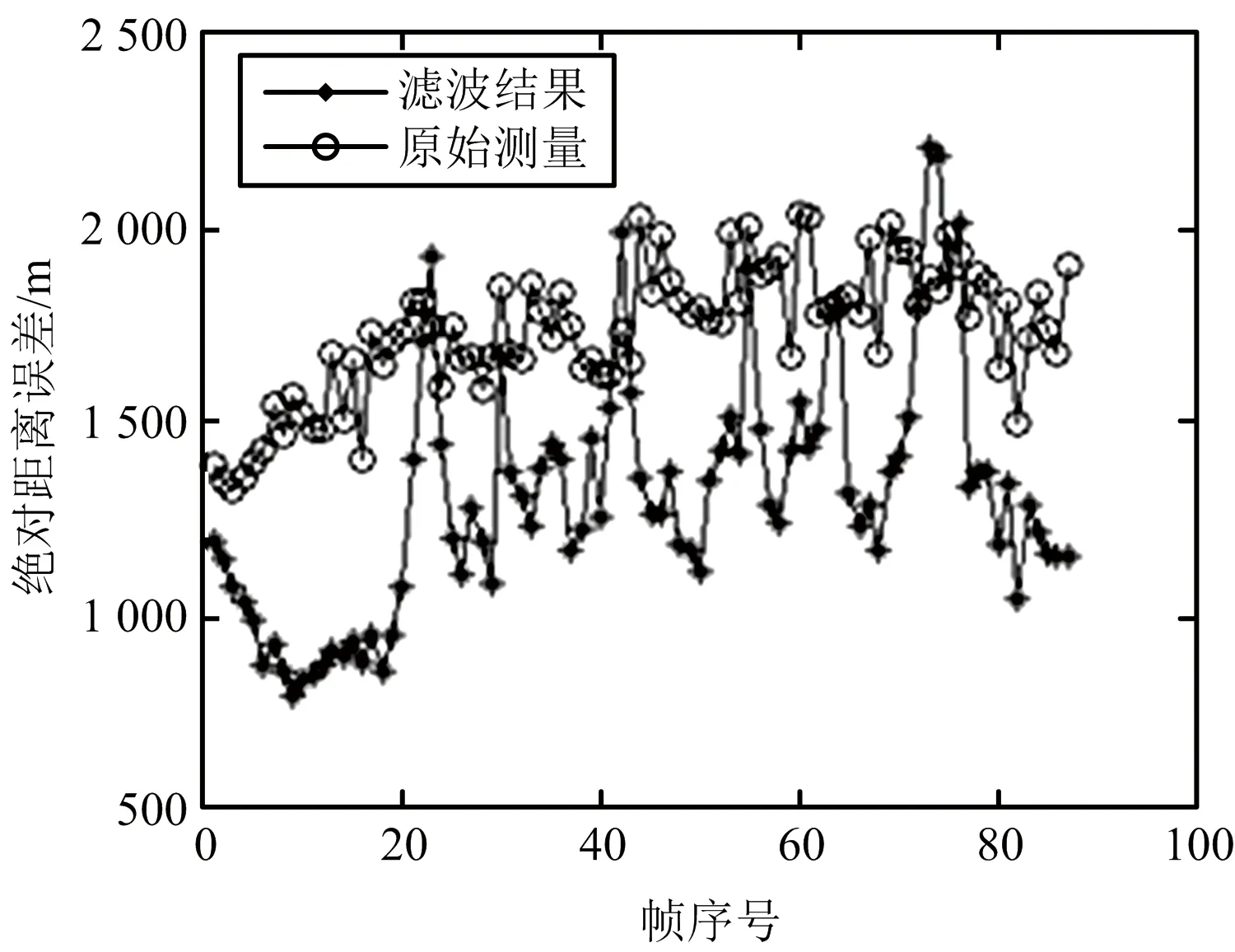
圖4 實驗二目標濾波前后誤差

5 結束語

本方法避免了模型與濾波器不匹配導致的濾波器精度嚴重下降，減少了平臺運動和坐標變換對量測誤差的影響。將多普勒速度應用到模型概率初始化和模型參數初始化中，進一步提高了濾波器的初始精度和可靠性。線性濾波采用線性卡爾曼濾波，非線性濾波采用容積卡爾曼濾波，既保證了濾波器的精度和數值穩定性，又使運算量最小。仿真實驗表明該算法提高了機載PD雷達的航跡情報質量，尤其是提高了航跡濾波的精度和穩定性。