基于參考位置指紋離散程度的WKNN定位方法*

趙 芳

(新鄉學院 計算機與信息工程學院， 河南 新鄉 453003)

人們對無線通信的需求隨著網絡科技的飛速進步呈現出多樣化特征，而位置服務[1-3]就是這些需求中最為關鍵的一項，然而位置服務會受到無線定位技術的限制.無線定位技術以地理位置為前提能夠進行室內和室外定位[4-5].通常情況下能夠經過北斗和GPS等衛星導航系統加以A-GPS輔助完成室外定位，且具有定位精度良好且效率高等特點.然而衛星信號穿透能力非常微弱，與此同時建筑物的墻壁也會對其產生阻撓作用，這在很大程度上使得衛星信號不能為室內設備提供定位服務.另外室內無線信號環境又非常繁雜，建筑物墻體和房間布局等很多因素都能致使無線信號產生多徑效應.

隨著智能手機等內部配置無線接入儀器的迅速發展，Wi-Fi信號已運用至大部分室內環境，同時以Wi-Fi技術為基礎的位置指紋定位可以利用無線接入點在建筑內相異坐標的信號強度值，構建位置坐標和離線信號強度的指紋數據庫，并將其作為在線定位的基礎[6-7].通常情況下此方式的定位精度和效率會受到離線指紋數據庫的有效性和位置相互匹配算法擾動的影響，因而本文提出了一種基于Wi-Fi指紋離散程度的WKNN定位算法(DD-WKNN算法).

1 離線位置指紋數據聚類

1.1 構建初始位置指紋數據庫

設構建某個定位區域離線位置指紋數據庫需有D個指紋信息采集點數據，同時其二維空間位置坐標為Li=(xi，yi)，i=1，2，…，D.各采樣點可得到N個無線接入點的信號強度值，即

Ri=(ri1，ri2，…，riN)

(1)

各組指紋信息的數據結構可以表示為

Fi=(Li，Ri)=(xi，yi，ri1，ri2，…，riN)

(2)

將采樣獲得的數據運用行方式完成保存，進而獲得其所有離線位置的數據庫，即

(3)

式中，xD和yD分別為D指紋信息采集點的橫坐標和縱坐標.

1.2 基于K-means算法的數據聚類

第一步：從D個指紋信息中隨意擇取K個指紋作為初始聚類中心集合C，且C=(C1，C2，…，CK)，Ci的數值與隨意擇取的位置指紋數據Ri(i=1，2，…，K)相等，即

C=(R1，R2，…，RK)

(4)

第二步：運算剩余的D-K個指紋和C中每個聚類中心Ci的歐氏距離，從而獲得與此指紋相對最為逼近的聚類中心Ci，隨之將其歸至此聚類中，進而獲得包括D個指紋信息的K個聚類，將各聚類中指紋信息個數定義為nCi(i=1，2，…，K).

第三步：重新運算K個聚類各自的聚類中心，隨后用其替換原有的聚類中心，即

(5)

式中，Rm為第i個聚類中第m個位置的指紋數據.

第四步：以此循環往復第二、第三步直至運算獲得的聚類中心值等于上個步驟的數值，換言之就是其收斂至極值，進而獲得最終離線位置指紋信息聚類[8-9].

2 DD-WKNN位置指紋定位算法

在基于參考位置指紋離散程度的WKNN定位算法中，需要在上述所得數據內擇取和在線實測RSSI值歐氏距離相對最為逼近的指紋數據，然后依照其離散程度設置位置估算參考權重的權值，令k個位置指紋的變異系數代表離散程度，隨之完成歸一化加權求和，其具體算法流程如下：

1) 在待定位位置實測各Wi-Fi無線接入點的RSSI采樣值，記為RL，其表達式為

RL=(rL1，rL2，…，rLn)

(6)

式中，rLn為第n個Wi-Fi無線接入點在此待定位位置的信號強度RSSI采集值.

2) 依照RSSI采集值搜索與之對應的離線位置指紋數據庫，利用式(7)擇取k個和RSSI采樣值歐氏距離最小的離線位置指紋數據庫Fk，即

(7)

(8)

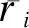
(9)

(10)

(11)

4) 將vi歸一化后轉化為權重系數wi，且二者關系為

(12)

5) 依照獲得的權重系數完成對每個參考點的加權求和運算以估算其位置坐標，即

(13)

DD-WKNN算法具體實現流程如圖1所示.

圖1 DD-WKNN算法流程圖

3 結果分析

擇取實驗地點為某大學能夠感知多個Wi-Fi無線接入點RSSI值的辦公區樓道，其Wi-Fi型號為AP6476，然后擇取一塊20 m×2 m的條形區域，此樓道區間能夠同時得到大于等于8個未知位置傳輸出來的接入點信號，同時可測得其RSSI值.擇取(0 m，1 m)～(20 m，1 m)作為待定位位置實際坐標區間，按照1 m間隔距離設定17個待定位位置，每間隔3 s完成一次各接入點信號的RSSI采樣值記錄，1 min后運算其平均值作為最終RSSI采樣值.待定位位置具體布置如圖2所示.

由于存在于所選區間房間內的Wi-Fi型號相同，同時每個房間都包含書桌、電腦和書柜等很多物體，且各房間門均為防盜門，因而所選區域Wi-Fi無線接入點的RSSI值可以認為是均勻分布的.在此區域內利用智能手機裝置Wi-Fi檢視儀獲取周圍Wi-Fi無線接入點的RSSI值[10].離線位置指紋數據的采樣點擇取樓道兩邊房間門所處的兩條直線上，在(0 m，0 m)～(20 m，0 m)和(0 m，2 m)～(20 m，2 m)坐標范圍內，每間隔1.5 m設定一個待測位置，且待定位位置總數為28，完成對8個Wi-Fi無線接入點RSSI值的采集后，取其平均值保存至指紋數據庫，設K-means算法的聚類數目為3，最終獲得的數據如表1所示.

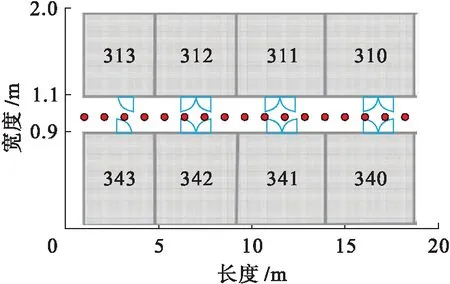
圖2 待定位位置布置

表1 指紋數據庫中的采樣點位置數據

為了檢驗從各位置采集到的Wi-Fi無線接入點數目對算法定位誤差的擾動程度，從Wi-Fi無線接入點中擇取4～8個點與最近鄰NN算法進行對比分析，兩種算法的定位誤差分布如圖3所示.

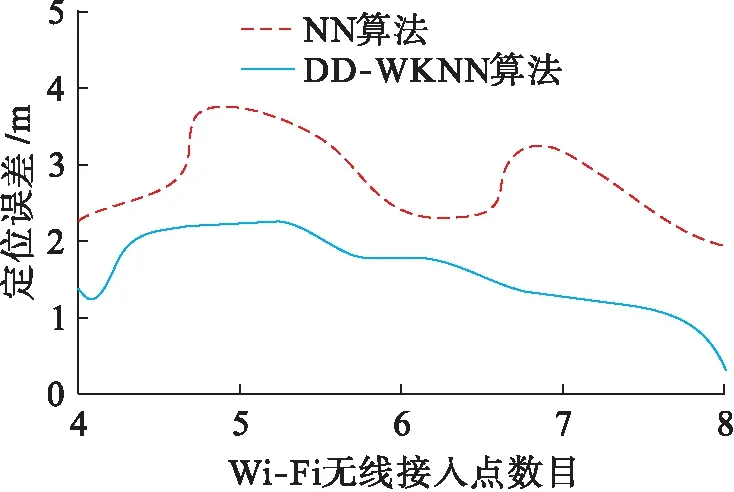
圖3 無線接入點數目的擾動箱線圖

由圖3可見，當參考Wi-Fi無線接入點數目從4擴增至8時，最近鄰NN算法[11]定位誤差中值約從3.4 m縮減至3 m以下，而DD-WKNN算法則約從2.5 m縮減至0.5 m，可見，參考Wi-Fi無線接入點數目對位置指紋定位具有一定擾動，同時表現出正相關關系，即隨著Wi-Fi無線接入點數目的不斷擴大，最近鄰NN算法和DD-WKNN算法的定位精度都有所改善.另外，在擇取一致的Wi-Fi無線接入點數目情況下，DD-WKNN算法定位精度高于NN算法，同時其誤差波動情況相對更小.

將本文算法、最近鄰NN算法和基于歐氏距離的傳統WKNN算法進行定位精度對比分析.分別在實驗區域的(0 m，0.5 m)～(20 m，0.5 m)和(0 m，1.5 m)～(20 m，1.5 m)坐標范圍內每距離1 m完成對待定位位置的RSSI值采集，且待定位位置總數為42.各采樣點每間隔1 min完成對各無線接入點RSSI值的10次采樣，同時擇取其平均值作為實際測量值，分別運用三種算法完成對待定位位置坐標的估算，各算法的誤差累積概率分布如圖4所示.

圖4 三種算法的實測性能對比

由圖4可知，最近鄰NN算法定位誤差具有較高的數值，誤差累積函數收斂速度相對最為緩慢，同時還具有相對較高的最大誤差值.基于歐氏距離的傳統WKNN算法的定位精度相比NN算法具有較大的優勢，其最大誤差值約為2.5 m.DD-WKNN算法的定位精度表現更加良好，其誤差累積函數具有很快的收斂速度，同時其最大定位誤差值約為1.6 m.綜上所述，DD-WKNN算法在很大程度上提高了定位精度，同時具有相對更小的誤差波動區間.

4 結 論

DD-WKNN算法將k個和待定位位置實際測量RSSI值歐氏距離相對最為逼近的指紋數據作為位置估計參照點，同時以其離散度作為權重系數的基礎，對k個位置指紋數據進行加權求和運算以完成位置估計.依照位置指紋離散度權重信息將離散度相對較小的位置指紋數據賦予相對較高的權重，這能夠在很大程度上防止Wi-Fi無線接入點由于室內布局導致RSSI值出現較大改變而引發的定位誤差問題.實驗分析結果表明：DD-WKNN算法的定位精度高于以歐氏距離作為權重系數的傳統WKNN算法和最近鄰NN算法，且DD-WKNN算法具有更小的誤差波動.