能量最優的航天器連續動態避障軌跡規劃

康國華，張 晗，魏建宇，吳佳奇，張 雷

(1. 南京航空航天大學航天學院微小衛星研究中心，南京 210001；2. 西安衛星測控中心，西安 710043)

0 引 言

對于航天器自主交會對接任務而言，安全軌跡指在相對運動的動力學理論指導下，從任務需求角度決定的航天器之間接近與逼近的軌跡。在軌跡規劃任務中[1]，空間障礙、測控條件等外部因素以及燃料消耗、機動時間、操作測量器件安全工作范圍等特定需求都是軌跡安全與最優規劃的約束條件。

相對運動的動力學特性研究通常忽略姿態運動，且多基于C-W(Clohessy-Wiltshire)線性相對動力學方程展開[2]。Luo等[3]提出了包含交會中不同類型脈沖約束、燃料約束以及地面站測控條件約束的相對軌跡優化模型，并結合浮點編碼遺傳和單純形算法的優點形成混合優化器，有效獲得了全局最優解。隨后，Zhang等[4]提出一種非線性的程序設計方法，該方法以消耗的推進劑為目標函數，利用遺傳算法對整數和實數的編碼算法結合獲得最優解，使整體規劃路徑滿足作戰約束，綜合性能較好。針對近圓軌道，朱彥偉等[5]通過綜合C-W方程、脈沖控制和優化理論，從C-W方程解析解構建航天器自然軌跡與受限軌跡數學描述，同時考慮碰撞避免，研究了全局繞飛和局部限制軌跡設計，并分析軌跡的能量消耗，給出了軌跡設計參數。李蒙等[6]在近圓軌道相對運動模型上，結合給定的初始條件，通過初值計算和精確解迭代步驟獲得了變軌控制參數，實現了航天器的自主變軌規劃。姚黨鼐等[7]將相對運動分解為視線瞬時旋轉平面內的運動與轉動，通過確定最佳機動方向使得航天器具有在空間目標距離較近時的自主規避能力，用于規避軌跡任務的基礎。

近年來，隨著電推進技術的發展，使最優控制理論可被用于軌跡規劃[8-11]，實現最小時間[12]和能量[13]的轉移軌跡。潘迅等[9]提出考慮地球扁率J2項攝動影響的小推力燃料最優軌道轉移方法，分別對動力學模型、推力大小和性能指標同倫；根據極小值原理推導最優控制律，得到小推力燃料最優轉移軌跡，有效解決了J2項攝動引起的系統非線性強、算法不收斂等問題。姚瑋等[10]提出一種基于連續推力并將貝塞爾曲線與軌道形狀方程相結合的平面機動軌道設計方法，將累計速度增量作為優化指標函數，并利用優化算法得到了最優機動軌道，解決了限制時間約束的平面軌道交會問題。Richards等[11]通過優化二進制變量，將必要邏輯約束附加到燃料優化的線性程序中，提出了一種能夠有效躲避空間障礙或其他運載工具的航天器燃料最優軌跡規劃方法。上述研究逐步擺脫了早期只考慮算法本身，不考慮推力器實際能力的弊端，更加接近工程實際。

然而，空間中失效航天器與碎片的動態變化，給轉移軌跡帶來新的威脅和挑戰。上述文獻[3-7,9-11]對基于C-W方程、最優控制的轉移軌跡規劃均有一定成果，但未考慮空間障礙物動態的情況。本文在在軌航天器軌道規避體系研究的指導下[14]，提出了一種能量最優的連續動態避障算法，該方法基于有限時間的相對運動能量最優模型，結合軌跡偏移和正態分布概率推導了包含安全距離約束的運動軌跡規劃模型；通過考慮碰撞風險，確定了動態避障點的選取規則，同時考慮能量約束問題，使航天器在有效規避動態障礙的同時盡可能減少燃料的消耗。

1 問題描述

追蹤航天器(Sat)要在有限時間完成軌道轉移，追上目標航天器(Tar)(如圖1)，要求規劃的軌跡滿足空間相對運動動力學，能夠躲避空間中帶有一定速度的障礙物，同時實現能量最優，減少燃料的消耗。

圖1 追蹤航天器避障軌跡規劃Fig.1 Obstacle avoidance planning for tracking spacecraft

傳統的軌道躲避機動通常需要三個脈沖完成[15]，如圖2所示，主要存在如下問題：

1)避障次數與原軌跡發生碰撞次數一致，無法通過避一次障礙消除后續碰撞風險；

2)對控制器瞬時推力要求大，對控制器要求高；

3)在時間固定的轉移任務中，需要消耗大量燃料以完成任務。

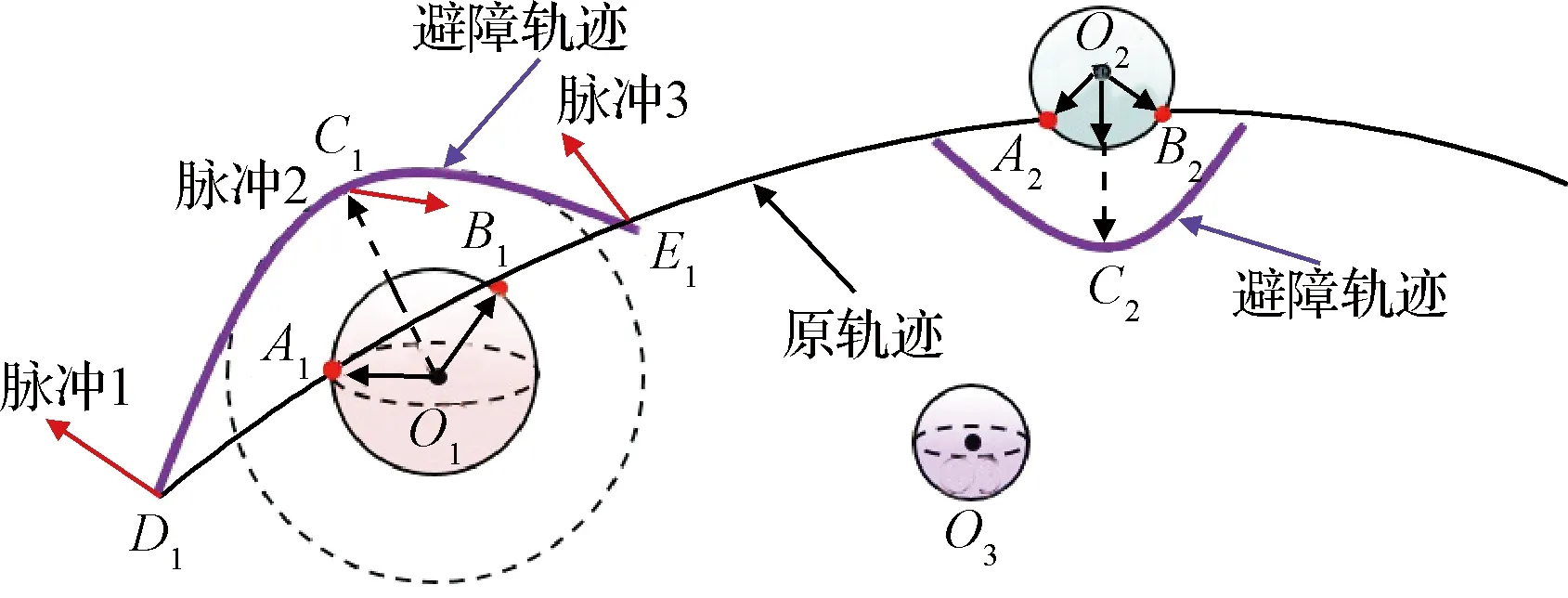
圖2 三脈沖避障策略Fig.2 Three-pulse obstacle avoidance strategy

鑒于燃料的重要性，航天器動態避障需要考慮能量最優、燃料最優。同時，為簡化追蹤航天器與目標航天器之間的動態避障軌跡規劃問題模型，不失一般性，做如下假設：

1)地球為均質球體，完全中心引力場；

2)航天器與空間物體(障礙物)在空間中所占區域用半徑已知的球體表示；

3)航天器在近地圓軌道上運行；

4)追蹤航天器相對目標航天器的距離遠小于目標衛星軌道半徑；

5)目標航天器未施加主動控制，追蹤航天器具有機動能力(各個方向均安裝推力器，可提供任意矢量方向的推力，施加推力前不需要建立點火姿態)。

2 能量最優相對軌跡規劃

2.1 相對運動建模

本文的追蹤航天器與目標航天器滿足C-W方程要求，建立以目標航天器質心Ot為原點的相對坐標系：Xt軸與目標航天器位置矢量r重合，由地心指向目標航天器；Yt軸在目標航天器軌道面內與Xt軸垂直，沿運動方向為正；Zt軸垂直與軌道平面，與Xt軸，Yt軸構成右手系。軌道相對運動方程為：

(1)

式中：x,y,z為目標軌道坐標系中追蹤航天器的位置分量；ux,uy,uz為追蹤航天器的軌道控制加速度；n為目標航天器軌道角速度。

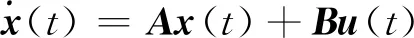
(2)

2.2 能量最優下的相對運動規劃

路徑明確下的軌道機動通常需要考慮能量、時間等綜合因素對目標進行優化，應用最優控制理論建立如下有限時間能量最優性能指標[16]，如式(3)。

(3)

式中：t0和tf分別為初始時刻和終端時刻。根據最優控制理論基礎方程[16]，推導出能量最優下的位置與速度模型如式(4)所示。

(4)

3 連續動態避障軌跡優化

3.1 規避障礙安全距離建模

在上述規劃路徑上，如存在動態障礙物，則需進一步考慮動態避障問題。雖然在初始時刻即考慮障礙物位置與速度進行軌跡規劃，但由于空間中存在的各種影響以及C-W方程局限性，最終有可能導致對障礙物軌跡預測出現誤差累計，從而發生偏移，導致結果如圖3所示。本文在能量最優規劃基礎上，融合軌跡偏移誤差模型和正態分布模型，建立了動態障礙物軌跡偏移下的規避障礙安全距離模型。

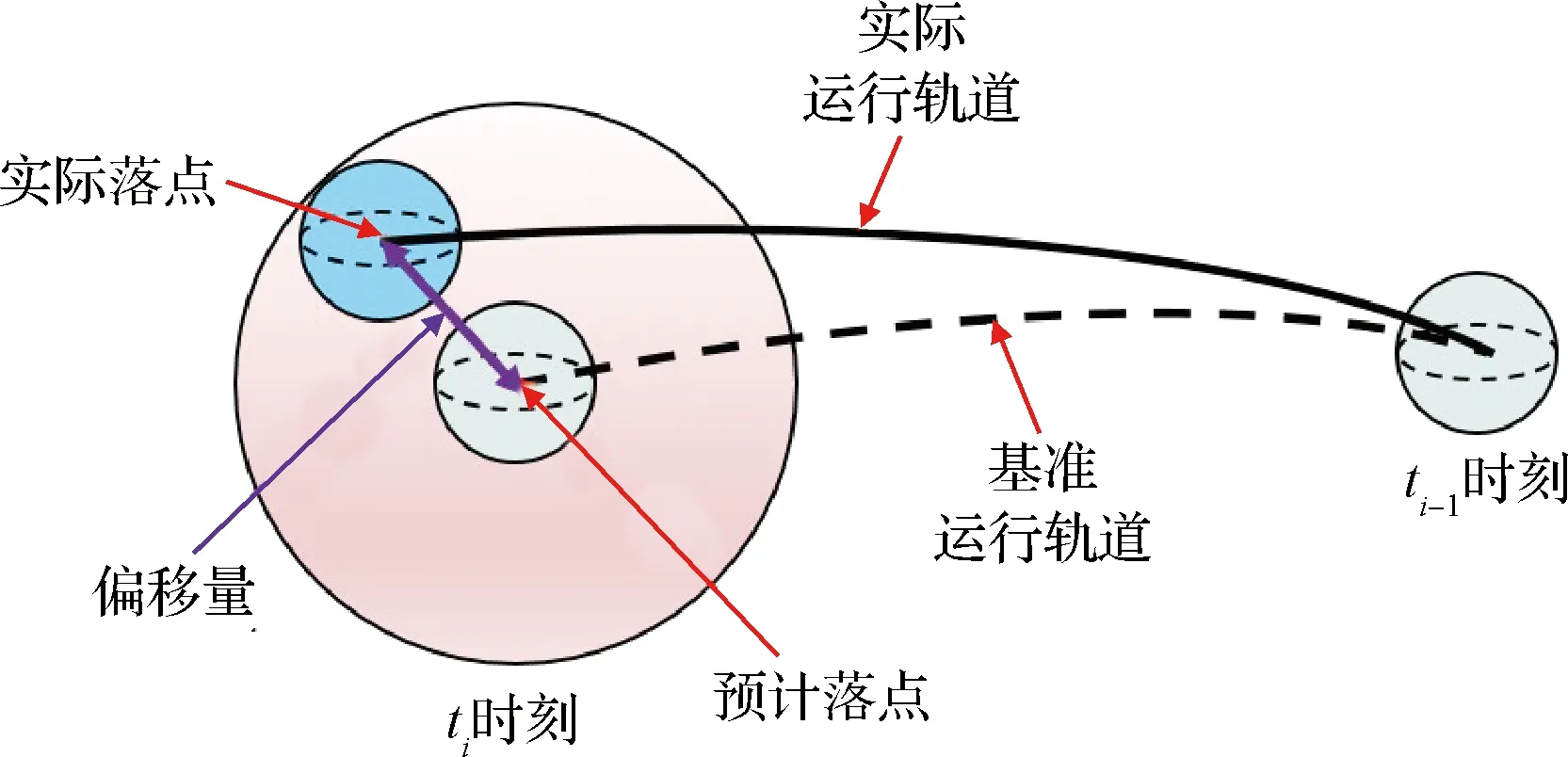
圖3 累計誤差導致的軌跡偏移Fig.3 Trajectory shift caused by cumulative error

在沒有施加控制量時，可以根據初始時刻狀態向量求得任意時刻障礙物的相對狀態量值，如式(5)所示[3]，即可獲得障礙物隨規劃時間變化的狀態量。

X(ti)=Φ(ti,t0)X(t0)

(5)

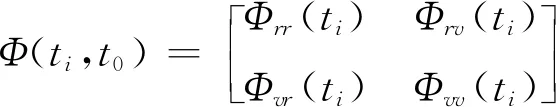
由于C-W方程的線性化誤差、小偏心率誤差以及攝動誤差主要體現在切向(y向)[17]上，包括位置預報的長期誤差和周期性誤差；x與z向誤差均為周期項且小于y向，所以本文主要考慮y向的偏移，如式(6)。

(6)

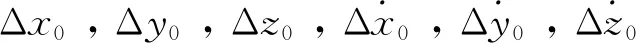
在考慮動態障礙物軌跡偏移基礎上，基于如下假設構建規避障礙安全距離模型：障礙物軌跡偏移服從正態分布模型[18]，障礙物包圍球半徑(期望)μ(t)=ro(t)=ro(t0)+|Δy(t)|，隨時間逐漸變大；時間越長，預報的準確性降低，設規劃t0～tf時間間隔內，期望處概率在f(μ(t))∈[ξ0,ξf]之間(該值相當于疊加了擾動，該值越小說明對預報軌道的信賴度越低)，求解該時間段內方差σ(t)范圍。根據追蹤航天器規避障礙準確率，使其軌跡始終保持在障礙中心距離(期望)對應的σ(t)之外即可。

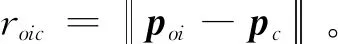
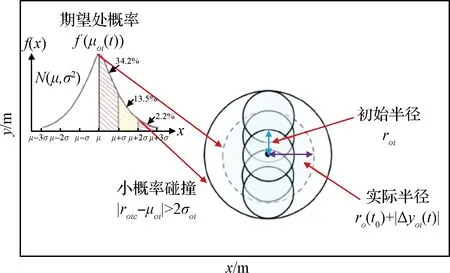
圖4 z軸視角下的規避障礙安全距離模型Fig.4 Obstacle avoidance safety distance model from z-axis perspective

3.2 避障點選取

通過構建規避障礙安全距離模型，可在每一時刻獲得追蹤航天器與障礙物避免發生碰撞的最小安全距離。若障礙物具有一定速度殘留，為防止碰撞，需對其與追蹤航天器的速度矢量進行分析，提高規避障礙的效率，降低后續碰撞發生概率，構建動態避障點選取模型如圖5所示。原軌跡為初始規劃軌跡，與障礙物O的包絡相交于A，B點。

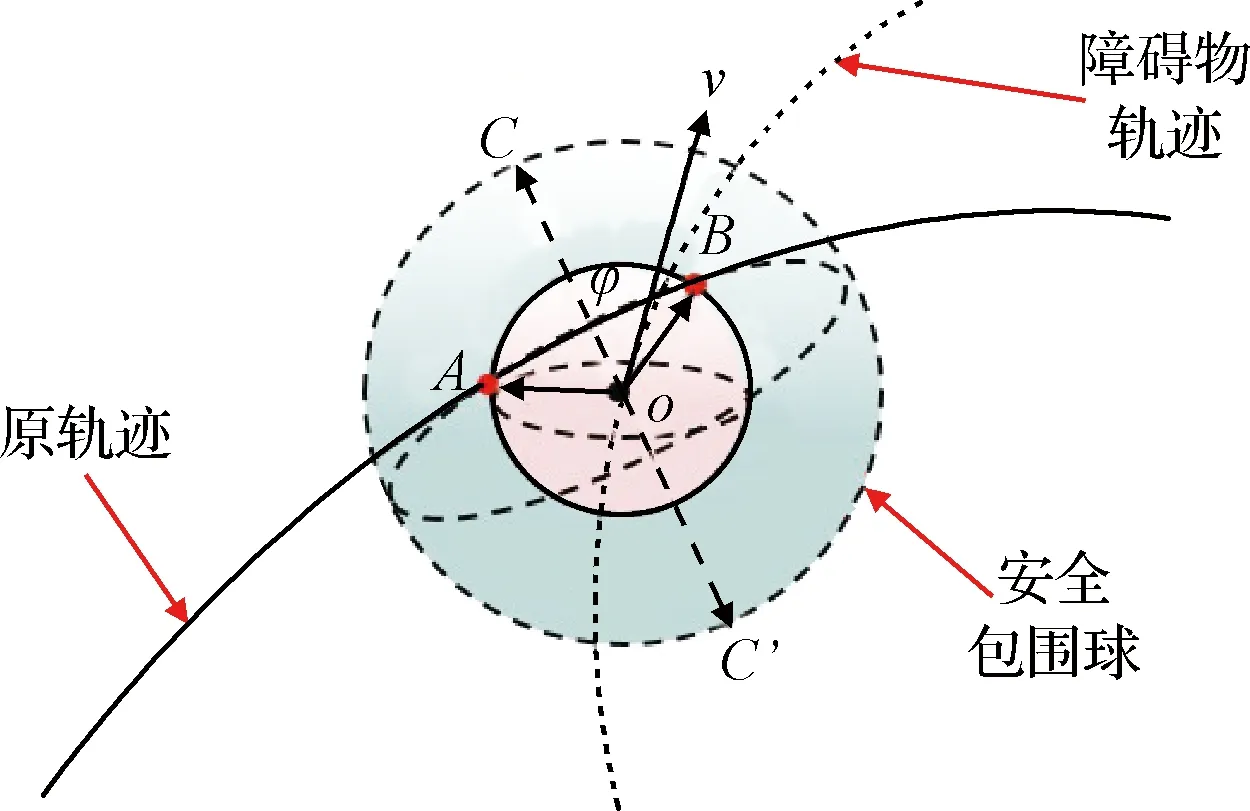
圖5 動態避障點選取Fig.5 Dynamic obstacle avoidance point selection

(7)

令cosφ=

(8)

取e′OC為eOC的最終值，由3.1節確定障礙物球心到避障點長度為rc=μoi(t)+2σoi(t)，此時避障點C的慣性系位置矢量Pc如式(9)所示：

Pc=(kcrc)eoc+Po

(9)

式中：Po為故障物質心慣性系位置矢量，kc為追蹤航天器安全系數，將其視為質點時kc=1；若考慮為有大小的物體時，kc>1。

3.3 連續動態修正能量最優避障策略

如3.2節避障點選取，已知唯一確定點C位置矢量，于是構建動態修正避障示意圖如圖6所示。

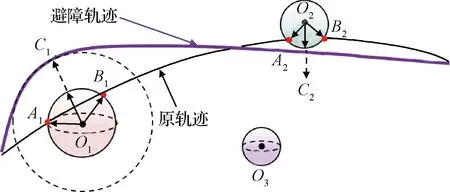
圖6 動態修正避障Fig.6 Dynamic correction obstacle avoidance

原軌跡在與第一個障礙物相交產生避障點C1后，將會根據下一個障礙物情況實時生成新的避障點C2，經過這樣多次修正，規劃的軌跡將始終滿足實時的能量最優的要求。于是，結合3.1節和3.2節，構建連續動態避障點優化如圖7所示。

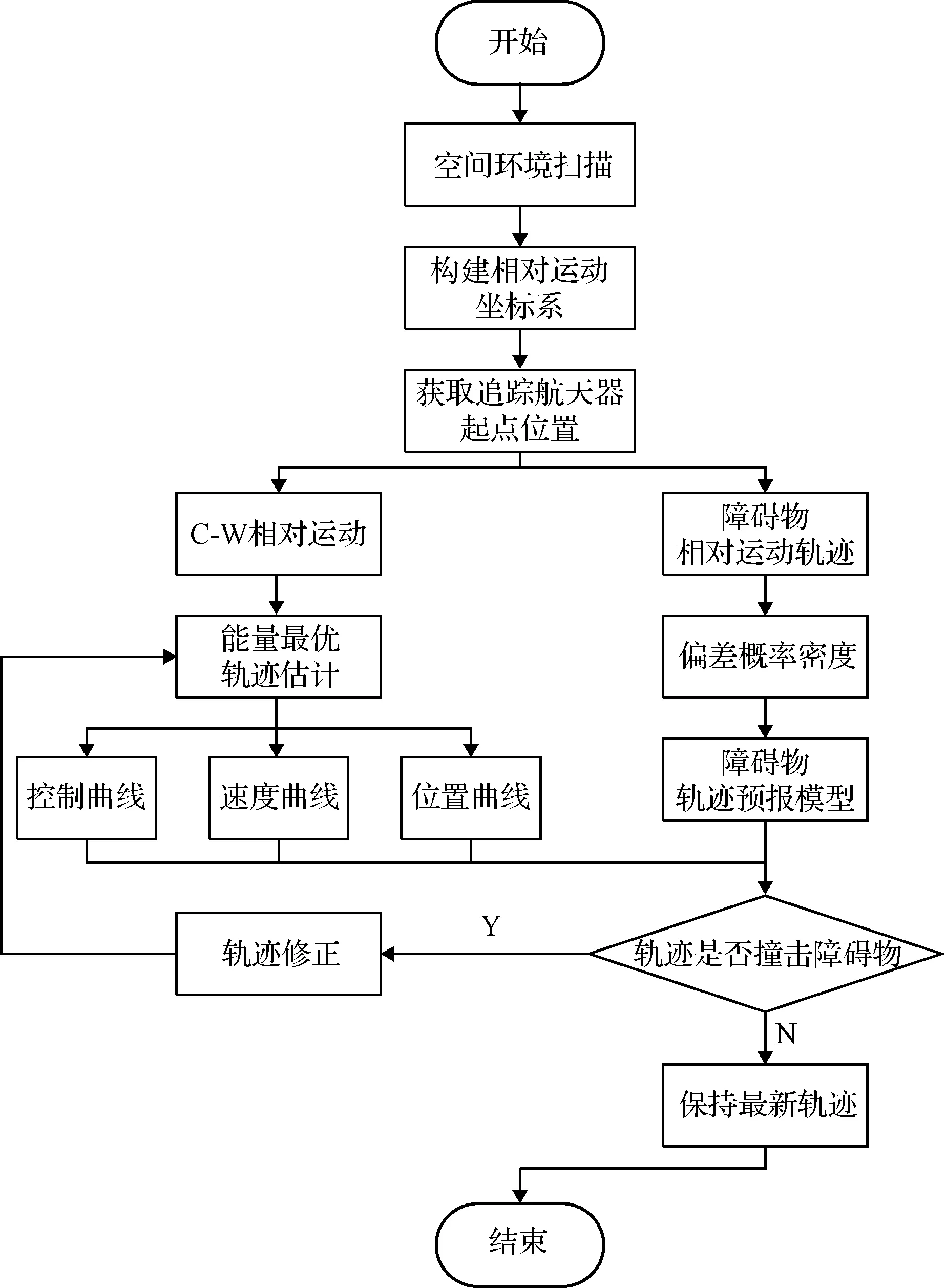
圖7 連續動態避障算法Fig.7 Continuous dynamic obstacle avoidance algorithm

根據圖7，軌跡修正部分的具體算法步驟如下：

1)根據原軌跡與各障礙物預報軌跡在時間間隔t0～tf進行碰撞判斷，若發生碰撞則i=i+1(i的初始值為1)，進入步驟2)，否則退出進入步驟6)；

2)尋找時間序列中最近的時間toi以及其對應A與B點位置矢量；

3)根據障礙物當前速度矢量以及軌跡預報生成的規避概率確定唯一修正點C，點C位置矢量與時刻toi確定，速度矢量為原軌跡中toi對應速度；

4)根據時刻toi為界，將規劃問題分為初始時刻為t0終端時刻為toi以及初始時刻為toi終端時刻為tf的兩段軌跡規劃，并更新原軌跡；

5)判斷t0～toi間隔輸出的原軌跡(已更新)是否與障礙發生碰撞：

(1)若發生碰撞則不改變i的賦值，使原軌跡為t0～toi間隔輸出的原軌跡并進入步驟2)；

(2)若未發生碰撞則使原軌跡為toi～tf間隔輸出的原軌跡，后令t0=toi，進入步驟1)。

6)最終將軌跡中每個時間段的性能指標按照如式(3)相加用以描述軌跡規劃性能并輸出軌跡。

4 仿真校驗與分析

4.1 仿真參數設置

為了對所提出的避障方法進行仿真校驗，利用Matlab構建算法程序，整個運行環境如表1所示。

467例急性心肌梗死β受體阻滯劑的應用狀況及影響因素分析………………………… 陳瑾瑾，劉培延，張 倩（5·371）

表1 仿真環境參數Table 1 Simulation environment parameters

本節以追蹤航天器躲避障礙物且接近目標航天器為例進行仿真，目標航天器為近圓軌道運行，其在慣性坐標系下的初始狀態參數、以及仿真環境參數設置如表2所示。

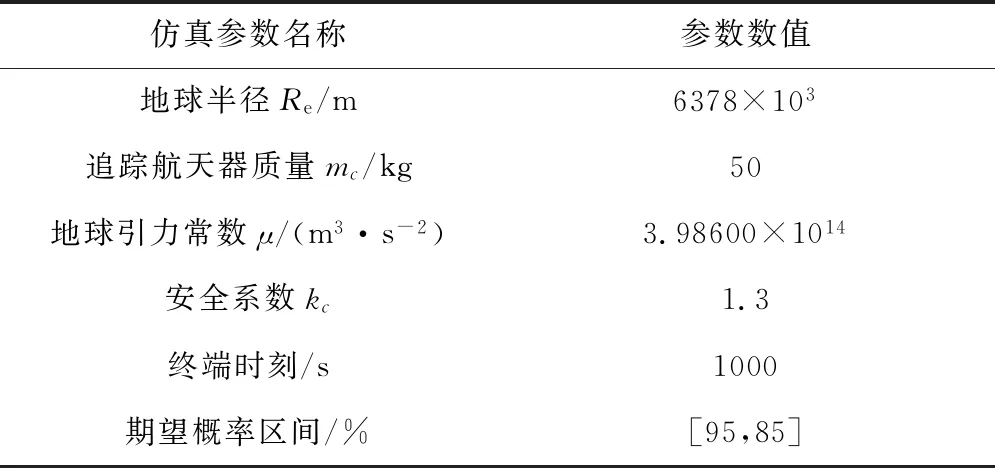
表2 仿真參數設置Table 2 Simulation parameter setting

在本例中，追蹤航天器與目標航天器處于異面狀態，根據空間近距離路徑規劃要求，兩航天器之間的相對距離不得超過10 km。于是，設置兩航天器的初始軌道根數如表3所示；兩航天器在地心慣性坐標系下的初值如表3所示；兩航天器在相對坐標系下的初始值如表5所示。同時，設置空間動態障礙物的數量為5個，初始狀態與誤差如表6，表7所示。

表3 兩航天器的初始軌道根數Table 3 Number of initial orbits of two spacecraft

表4 兩航天器在地心慣性坐標系下的初值Table 4 Initial values of the two spacecraft in the geocentric inertial coordinate system

表5 兩航天器在相對坐標系下的初值Table 5 Initial values of two spacecraft in relative coordinate system

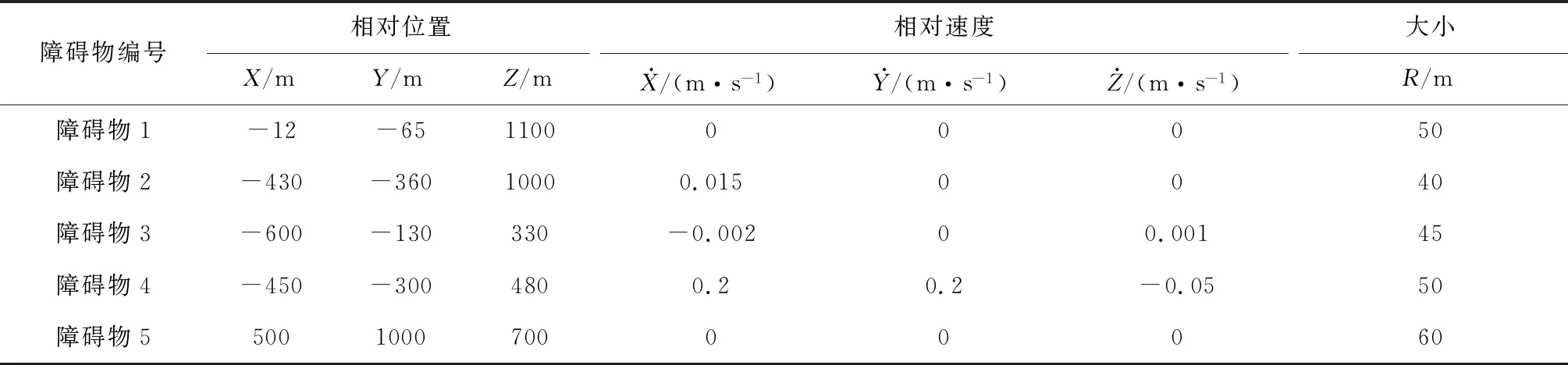
表6 障礙物在相對坐標系下初始狀態Table 6 Initial state of obstacles in relative coordinate system

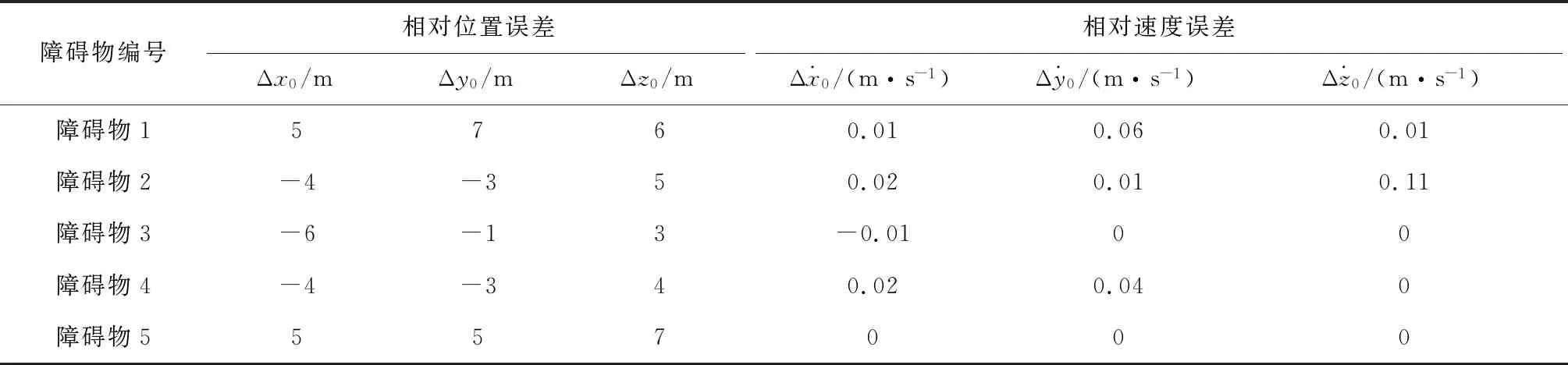
表7 障礙物在相對坐標系下初始狀態誤差Table 7 Initial state error of obstacle in relative coordinate system

4.2 仿真與分析

根據表1～6進行仿真環境初始化，對能量最優的航天器連續動態避障軌跡規劃算法進行仿真驗證，并根據表7與式6獲得了5個動態障礙物y向誤差偏移量(如圖8)。

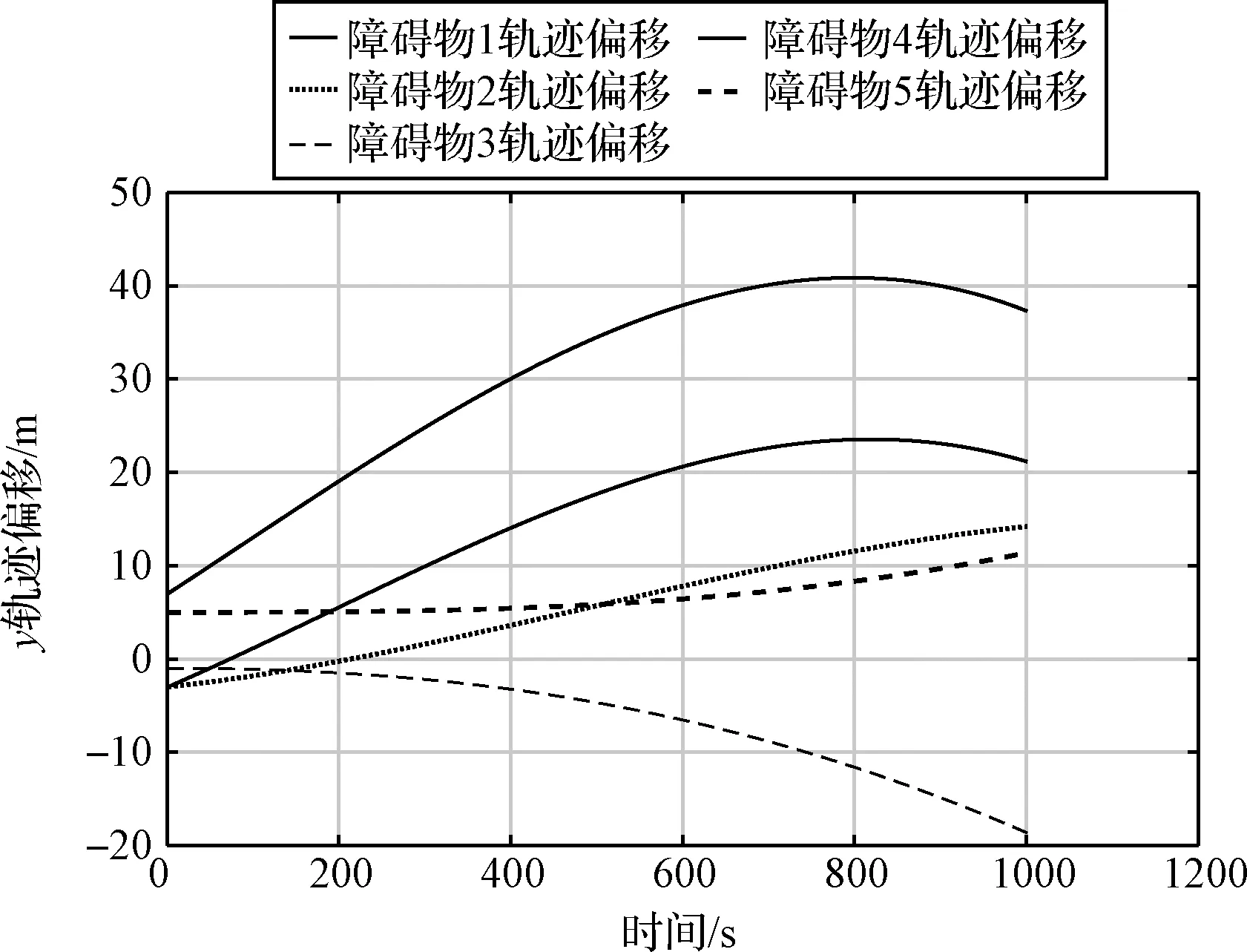
圖8 動態障礙物軌跡偏移量Fig.8 Dynamic obstacle trajectory offset

根據圖7算法流程構造的連續動態避障軌跡規劃算法，輸出的動態避障軌跡的哈密頓函數曲線與軌跡如圖9～10所示。從圖9中可以看出，追蹤航天器每段成功避障后的軌跡均通過哈密頓曲線能量最優的驗證，且在時刻t1=192s和t2=638 s時進行了有效的避碰操作，累計規避兩次障礙。

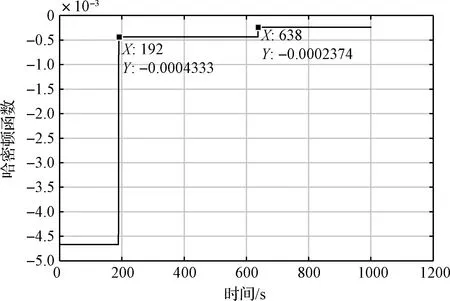
圖9 動態障礙規避中的哈密頓函數Fig.9 Hamiltonian function in dynamic obstacle avoidance

從圖10可以看出，原軌跡(未設置動態障礙的軌跡，虛線)會與3個障礙物(障礙物1、3、4)前后發生碰撞；而經連續動態避障算法優化后的轉移軌跡(實線)，能夠根據避障點選取規則確定的避障點(圖中五角星標記)有效地規避空間動態障礙，并且成功排除1次原有的碰撞風險。同時，為完整呈現整個動態仿真過程，對追蹤航天器與每個障礙物的實時距離與安全距離進行模擬，如圖11所示。

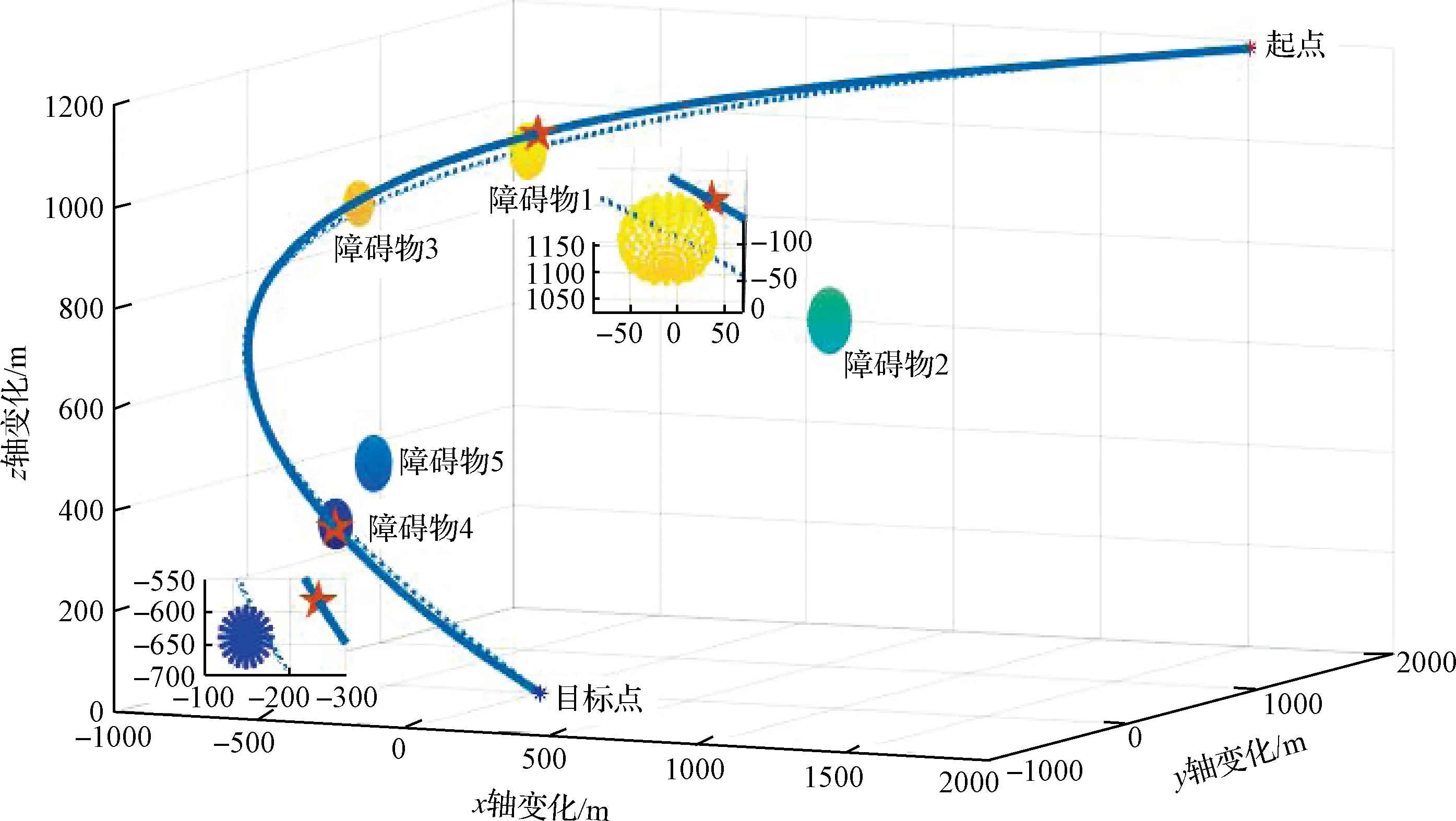
圖10 連續動態避障軌跡Fig.10 Continuous dynamic obstacle avoidance trajectory

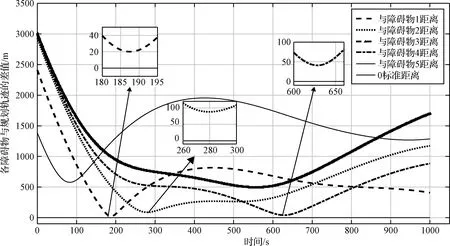
圖11 航天器與障礙物距離曲線Fig.11 Distance curve between spacecraft and obstacles

為描述直觀，將圖11中3個有碰撞風險的障礙物包絡與追蹤航天器質心之間的距離曲線放大，如小圖所示：3個障礙物與追蹤航天器之間的距離在動態過程中始終保持在安全距離(0標準距離)之外，有效地躲避了碰撞的發生。

考慮工程實際，根據工質燃料消耗公式，假設追蹤航天器推進器比沖Isp=3000 s(現有的推進系統很容易達到[20-21])，可獲得避障過程中消耗的實際工質,基于此得出如表8的統計分析。

表8 有無動態避障的速度增量與工質消耗對比Table 8 Comparison of speed increase and working fluid consumption with or without dynamic obstacle avoidance

從表6看出，追蹤航天器通過規避2個障礙物得出的軌跡，其性能指標增加了3.77%，速度增量增加0.65%，工質消耗增加了0.77%。因此，動態避障軌跡規劃算法能夠通過增加微量燃料消耗，來滿足規避動態障礙的任務要求。

5 結 論

本文提出的能量最優實時動態避障算法，能夠實現障礙物具有動態不確定性下的能量最優軌跡轉移。根據空間相對運動特殊性，本文融合線性相對運動方程與有限時間的能量最優模型，推導了相對運動能量最優模型。考慮空間障礙物動態變化，將其y向誤差偏移與中心正態分布概率引入規避障礙安全距離模型中，確定追蹤航天器的軌跡禁區，給出最小安全距離。同時，提出一種動態避障點的選取規則，對避障點的具體位置進行了幾何約束，有效減小后續碰撞發生概率的同時使燃料的消耗盡可能最少。仿真驗證表明，連續動態避障算法符合能量最優性，具有較高的安全性和可靠性。