能量守恒定律在Boost變換器分析中的應用

李湘峰， 屈莉莉， 莊梓丹， 張惠桃

(佛山科學技術學院 機電工程與自動化學院，廣東 佛山 528000)

0 引言

隨著社會經濟的發展和科學技術的進步，電力電子技術在電動汽車、機器人以及智能電網等領域得到了越來越廣泛的應用。雖然電力電子技術在我國的現代化建設中意義重大，但我國電力電子技術相關人才卻一直較為缺乏，因此，通過高效的“電力電子技術”課程教學培養高素質的電力電子技術研發人員具有較大的現實意義。

電力電子技術涉及電力技術、電子技術、電磁技術以及控制技術等相關學科，知識結構復雜、所需知識點跨度較大而難以理解，對教師的授課技巧與學生對知識的接受能力提出了較為嚴峻的挑戰。以Boost變換器為例，目前，“電力電子技術”教材[1，2]對于Boost變換器的分析方法較為統一，其分析過程中運用到的電學理論較多，主要包括伏秒平衡、電磁感應以及面積等效原理等。學生對部分理論知識點較為陌生，對相關公式的理解不夠深刻、從而導致學習效果差強人意。實踐證明，若能從學生較為熟悉的理論知識入手對Boost變換器進行分析，最終再與教材現有分析方法進行對比學習，即可取得較好的教學效果[3～5]。調查表明，電子電氣類學生對于自然界的三大守恒定律，特別是能量守恒定律相對比較熟悉，且能量守恒定律在電力電子前沿技術研究方面也獲得了較成功的應用[6]，基于此，本文擬采用學生較為熟悉的能量守恒定律作為理論工具，對Boost變換器的工作特性進行分析與計算，以期為“電力電子技術”課程的教學提供一種新的思路。

1 Boost變換器工作特性分析

圖1所示Boost變換器廣泛應用于新能源發電、電池管理系統以及功率因數校正等領域，屬于電力電子學科三大基本DC/DC變換器拓撲之一。

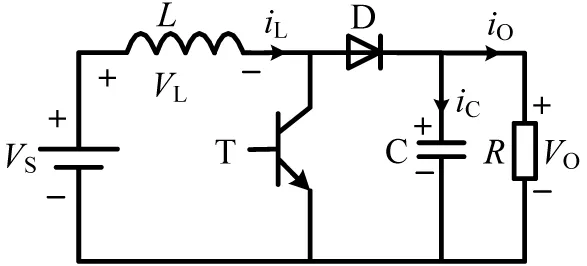
圖1 Boost變換器電路結構

若不考慮Boost變換器的潛電路工作模式[7]，可認為該變換器存在兩種基本工作模式，即電感電流連續模式CCM(Continuous Current Mode)和電感電流斷流模式DCM(Discontinuous Current Mode)。電感電流連續模式，即電感電流在整個開關周期內均大于0而保持連續，該模式下Boost變換器電路存在兩個電路狀態，其等效電路如圖2所示。

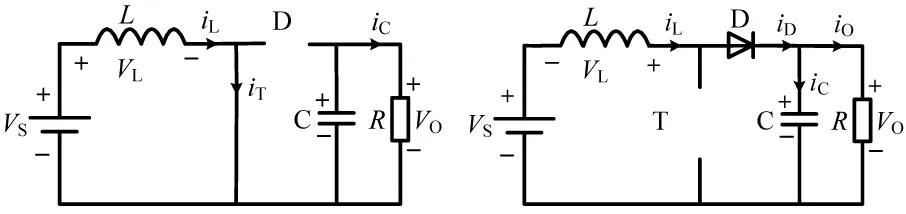
(a)電路狀態1 (b)電路狀態2圖2 電感電流連續模式下Boost變換器等效電路

電感電流斷續模式，即電感電流在某一時間段為0而斷流，該模式下Boost變換器電路存在三個電路狀態，相比電感電流連續模式其主要區別在于存在一個電感、開關管以及二極管均無電流流通的過渡狀態，其等效電路如圖3所示。

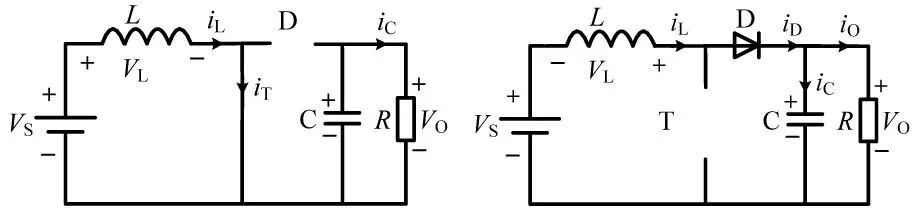
(a)電路狀態1 (b)電路狀態2

電感電流連續模式下Boost變換器典型電路波形如圖4(a)所示。波形從上至下依次為開關管T門極驅動波形VG、電感L的電流波形iL、開關管T的電流波形iT、二極管D的電流波形iD以及電感L兩端的電壓波形VL。電感電流斷續模式下，上述參量波形如圖4(b)所示。

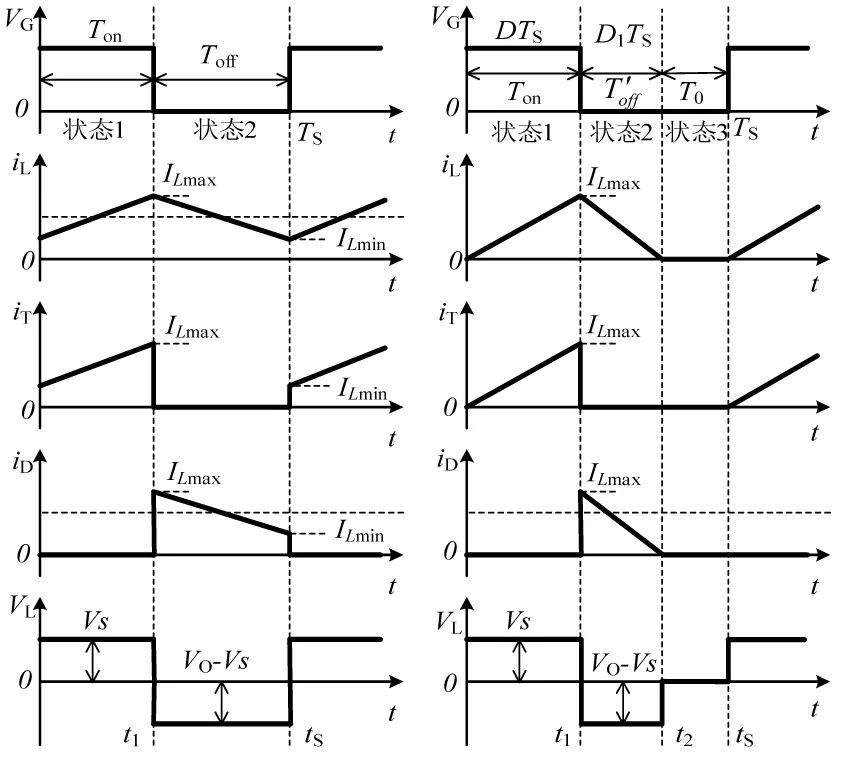
(a)電感電流連續 (b)電感電流斷續圖4 Boost變換器主要工作波形

2 Boost變換器增益函數的求解

2.1 電感電流連續模式

電感電流連續模式下Boost變換器等效電路及其工作波形如圖2及圖4(a)所示，該模式下Boost變換器擁有2種電路狀態。

(1)電路狀態1：開關管T導通、二極管D截止，此時Boost變換器等效電路如圖2(a)所示。此狀態下，電源電壓VS作用于升壓電感，使得電感電流iL線性增長。根據電磁感應定律，在此期間電感電壓滿足方程：

(1)

(2)開關狀態2：開關管T截止、二極管D導通，此時Boost變換器等效電路如圖2(b)所示。此狀態下，電壓源VS以及電感電流iL一起向負載及電容供電。假定輸出電容足夠大，即輸出電壓VO在一個開關周期TS中恒定不變，則在開關管T截止期間，電感電壓滿足方程：

(2)

電路達到穩態時，電感需滿足伏秒平衡原則，即：

VL_Ton·Ton+VL_Toff·Toff=0

(3)

將式(1)、式(2)代入式(3)可得：

VS×Ton=(VO-VS)×(1-D)TS

(4)

其中D=Ton/TS為占空比，化簡得：

(5)

式(5)即為電感電流連續模式下Boost變換器的增益函數，從式(5)可見，電感電流連續模式下，Boost變換器的電壓增益僅與占空比有關。

2.2 電感電流斷續模式

電感電流連續模式下Boost變換器等效電路及其工作波形如圖3及圖4(b)所示，該模式下Boost變換器擁有3種電路狀態。

(1)電路狀態1：開關管T導通、二極管D截止，其等效電路如圖3(a)所示。該狀態持續時間為Ton，該狀態下電感兩端電壓被輸入電源鉗位至VS，其電壓方程如式(1)所示。

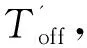
(6)

(3)開關狀態3：開關管T與二極管D均截止，其等效電路如圖3(c)所示。該狀態持續時間為TO在此期間電感電流iL保持為0，電感兩端電壓也為0。在整個開關周期中，電感依舊遵守伏秒平衡原則，即有：

(7)

在開關狀態3期間，電感電壓為VL_TO=0，因此有：

(8)

化簡后可得：

(9)

式中D1=Toff/TS。

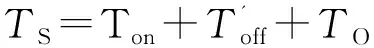
(10)

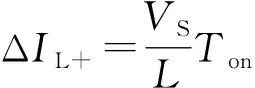
(11)

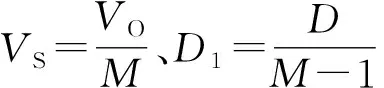
2LfSIOM2-2LfSIOM-VD2=0

(12)

運用求根公式求得電感電流斷續模式下Boost變換器的電壓增益為

(13)

由式(13)可見，電感電流斷續模式下Boost變換器的電壓增益不僅與占空比相關，還與輸出電壓、負載電流、開關頻率以及電感值大小等有關。

3 變換器分析中能量守恒定律的運用

由前述分析過程可見，Boost變換器電壓增益計算較為繁瑣，計算過程中運用了伏秒平衡、電磁感應以及面積等效等理論知識，若對上述理論知識不熟悉或理解不夠深刻，將對學習效率產生較大影響。因此，若從學生較為熟悉的能量守恒定律著手分析Boost變換器的電壓增益將會取得較好的教學效果。

3.1 電感電流連續模式

(1)電路狀態1：等效電路如圖2(a)所示。此狀態下，電源電壓VS作用于升壓電感并對其充電，使得電感電流iL線性增長。iL的增量△iL+可表示為：

(14)

(2)電路狀態2：等效電路如圖2(b)所示。此狀態下，電壓源VS以及電感電流iL一起向負載及電容供電。假定輸出電容足夠大，輸出電壓VO在一個開關周期TS內恒定不變，在此條件下，iL在Toff=TS-Ton時間內的減少量△iL-為：

(15)

根據能量守恒定律，電感增加(吸收)的能量與電感減少(釋放)的能量必定相等，則有：

(16)

即

(17)

化簡可得：

(18)

顯然，式(18)所示結果與目前教材所得分析結論一致。

3.2 電感電流斷續模式

(1)開關狀態1：等效電路如圖3(a)所示，此時電源VS對電感L充電，持續時間為DTS，此狀態期間，電源提供的能量可表示為：

(19)

(2)開關狀態2：等效電路如圖3(b)所示，在此狀態下，電源VS與電感L一起為輸出電容與負載提供電能，持續時間為D1TS。電感電流iL的減少量△iL-為：

(20)

此狀態結束時，在開關狀態1中所儲存的電能完全得以釋放，由于電感充放電過程也遵循能量守恒定律，因此電路狀態1中所充入的電能必定等于電路狀態2期間所釋放的電能，即有

(21)

將式(19)、式(20)代入式(21)得：

(22)

化簡可得：

(23)

在開關狀態2期間，電源 持續對負載提供能量，所提供的能量為電源輸出電壓乘以電源輸出電流再乘以時間，即：

(24)

(2)開關狀態3：等效電路如圖3(c)所示，電感與電源停止對負載供能，負載由電容提供能量。

為便于分析，假設輸出電容足夠大且無功率損耗，輸出電壓在整個開關周期期間保持恒定，則負載在整個開關周期所消耗的電能為 ，根據能量守恒定律，負載所消耗的能量 必然等于電源所輸入的總能量 ，即：

(25)

經整理可得：

(26)

其中，fS=1/TS為開關頻率。將式(23)代入式(26)，并化簡可得：

(27)

運用求根公式，求得VS：

(28)

用VO除以VS并進行整理即可得到電感電流斷續模式下Boost變換器的增益函數：(李湘峰等文)

(29)

對比式(5)與式(18)以及式(13)與式(29)可知，根據能量守恒定律推導得出的Boost變換器電壓增益與目前教材所推導的電壓增益函數完全一致，從而印證了本文分析方法的正確性與可行性。

4 結語

合適的教學方法與分析思路往往能起到事半功倍的效果，為此，本文了提出了一種基于能量守恒定律的Boost變換器分析方法。教學實踐表明，相比于目前教材所采用的方法，應用能量守恒定律對Boost變換器進行分析，其過程更為直觀、易懂。應用本文所提出的分析方法與目前教材所采用方法進行對比驗證，還可加深學生對Boost變換器工作原理、特性的理解，從而有效地降低了學習難度，提高了學習效率。該方法不僅適用于Boost變換器的分析與計算，也適用于其他類型DC/DC變換器的分析與研究。