《隨機事件與概率》教學實錄與評析

蔡金梅 宋程

隨機事件廣泛存在于生活中，學生對隨機事件和概率都有一些體驗，但是認識不深.在這節課中，執教老師借助信息技術，引導學生進行概率試驗，促進學生對概率意義的理解，同時在教學中滲透隨機思想，讓學生探究計算簡單隨機事件概率的方法.

一、創設情境，導入新課

師：電影《我和我的祖國》正在熱播，一名教師組織學生去看電影，不小心多買了一張電影票，于是就有了這一幕.（播放視頻：小明聽說老師多買了一張電影票，就想問老師要.小紅也想要.小明不同意，認為多出來的那張電影票是他的.小紅認為這不公平.）

師：多出來的這張電影票是給小明還是小紅呢？請同學們利用桌面上的工具（硬幣、轉盤、撲克牌以及除顏色外大小相同的小球），設計一個體現公平原則的游戲，通過勝負來決定誰可以得到這張電影票.請將你的方案寫在導學案上.

生分小組合作設計游戲方案，完成導學案.

師：下面請各小組代表跟大家分享本小組設計的游戲方案（手機投屏，如圖1、圖2）.

師：這兩個小組用硬幣和撲克牌設計游戲，很不錯！

生：我們小組利用工具“轉盤”設計的方案是二人比賽旋轉轉盤，誰轉到轉盤上的數字1就算獲勝.

師：轉盤上共有10個數字，轉到每一個數字的可能性一樣嗎？請用一個數值表示轉到數字1的可能性大小.

生：轉到每個數字的可能性都一樣，可以用[110]表示轉到數字1的可能性.

師：很好，我們再來看這個小組設計的游戲方案.

生：我們小組利用的工具是“小球”，設計的方案是——往袋子里放入一個紅球和一個黃球，再從袋子里取出一個小球，若取出的是紅球則小紅獲勝，反之則小明勝出.

師：請你用一個數值表示摸到黃球的可能性大小.

生：可以用[12]表示.

【評析】執教老師利用微視頻展示生活中常見的問題，創設真實情境，引導學生設計解決問題的方案，初步感受生活中簡單的隨機現象，并用數值刻畫隨機事件發生的可能性大小.

二、實踐探究，交流新知

師：像這樣，用[12]，[110]表示一個事件發生的可能性大小，我們把這個數值稱為概率.請同學們在書中找到概率的概念.（課件出示概率的概念：一般地，對于一個隨機事件A，我們把刻畫其發生可能性大小的數值，稱為隨機事件A發生的概率，記為[P（A）]）

師：我們回顧最后一個小組設計的方案（左手拿一個紅球，右手拿一個黃球，兩個小球除顏色外大小均相同），如果將黃球換成較大的黃色海洋球，抽到黃球的概率還是[12]嗎？

生：不是，此時一定能摸出黃球，概率是1.

師：對.我們在計算隨機事件的概率時，要確保每一種結果出現的可能性相等.概率符號通常用大寫字母P表示，比如摸到黃球的概率記為P=[12].這里的[12]是怎么得來的呢？

生：袋子里只有紅球和黃球，并且球的大小和形狀相同，黃球占總數的一半，所以，發生的概率是[12].

師：說得好！如果有[n]個質地均勻、大小形狀都相同的小球，其中有[m]個黃球，那么，摸到黃球的概率是多少？

生：概率是[mn]，黃球有[m]個，占總數的[mn].

師：對.一般地，如果在一次試驗中，有[n]種可能的結果，并且它們發生的可能性都相等，事件A包含其中的[m]種結果，那么事件A發生的概率就是[P（A）=mn].請你思考，概率[P（A）]的取值范圍是什么？

生：0<[P（A）]<1.

師：誰有不一樣的想法？為什么這里不能取到0或者1呢？如果等于0，會是什么事件？如果等于1呢？

生：概率等于0是不可能事件，概率等于1是必然事件.

師：也就是說，在[P（A）]=[mn]中，由[m]和[n]的含義，可知0[≤][m][≤][n]，進而有0[≤][mn][≤]1.如果0[≤][P（A）][≤]1，特別地，當A為必然事件時，[P（A）]=1;當A為不可能事件時，[P（A）]=0.

師生小結：事件發生的可能性越大，它的概率越接近1;事件發生的可能性越小，它的概率越接近0.

【評析】在探索概率這一概念的形成、概率的計算公式以及概率的取值范圍過程中，執教老師讓學生經歷了從實際問題到數學問題的抽象過程，發展了學生的抽象思維;通過提問和追問，使學生全程參與數學知識的形成過程，無形中培養了學生的歸納推理能力.

三、開放訓練，體現應用

課件出示例1：盒子中有5個紅球，5個黃球，4個藍球，這些球除顏色外無其他差別，從盒子中隨機摸出1個球，求下列事件的概率：（1）摸出紅球的概率;（2）摸出藍球的概率;（3）摸出黃球或藍球的概率.

師：剛才我們知道了概率的計算公式，接下來請同學們完成例1（1），計算摸出紅球的概率是多少.

生：[514].

師：14表示什么？

生：球的總個數.

師：每種顏色的球出現的可能性相等嗎？

生：相等.

師：所以，我們可以這樣書寫（師板書解題過程如下）——

解：共有14種結果，它們出現的可能性相等.

∴[P]（摸出紅球）=[514]

請同學們按照這樣的格式完成例1中的（2）（3）.

師：我發現有的同學做第（3）題時是這樣寫的：[514+][414=914]，誰有不一樣的想法嗎？

生：盒子里總共有3種顏色的球，要摸出黃球或藍球，排除紅球即可，所以，可以寫成[1-514=914].

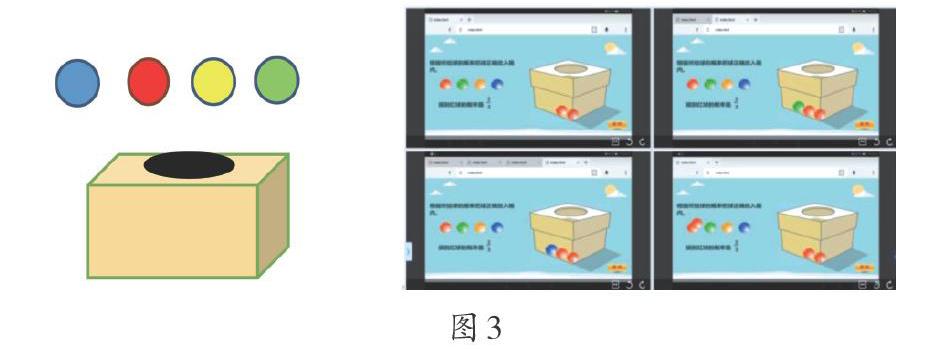
師：像這樣不是摸出紅球，就是摸出黃球或藍球的事件，我們將它稱為對立事件，可以用加法或減法來解決.現在，老師給出概率，你能知道盒子里都有哪些顏色的球嗎？（利用平板電腦的拖拽功能出示變式練習“摸球游戲”如下）.

如圖3，根據所給球的概率把球放入箱子：（1）摸到紅球的概率是[23];（2）摸到紅球的概率是[23]，同時摸到綠球的概率是[16].

師：我發現每個小組都有不同的想法，哪個小組來和大家分享你們的想法.

生：摸出紅球的概率是[23]，并不是說球的總個數是3，因此，可以同時擴大分子和分母的倍數.這道題可能有很多種情況.

師：說得好！概率反映的是一種比值關系，分母是3，并不表示只有3個球.如果增加一個條件，摸到紅球的概率是[23]，同時摸到綠球的概率是[16]，可以怎么擺放呢？

生：同時滿足兩個概率，那么球的總數是3和6的公倍數，分子對應乘倍數即可，如果球的總個數為6，紅球就是4個，綠球為1個，另一種球可以是黃球或藍球.

【評析】設計例題的目的是讓學生鞏固對概率意義的理解.要求學生計算簡單隨機事件的概率，理解指定事件發生所包含的試驗結果，這樣的教學有梯度也有針對性.變式練習設計了一個逆向的開放性的探究問題，執教老師利用平板電腦的拖拽功能，適時將信息技術融入教學，使學生進一步加深對概率意義的理解.

四、合作探究，深入學習

師：拋擲一枚質地均勻的硬幣，正面朝上的概率是0.5.拋擲20次硬幣，會有10次正面朝上，這個說法正確嗎？為什么？請同學們按照以下步驟，用實驗來驗證猜想.

小組合作探究：①二人一組，拋擲20次硬幣;②一名同學拋擲硬幣，一名同學記錄硬幣正面朝上的次數（有數字的為正面）;③拋擲硬幣過程中注意高度，避免硬幣掉在桌面和地面.

師：有的小組記錄硬幣正面朝上的次數是10次，有的小組記錄的是15次，有的小組記錄的是11次.只是單純地實驗20次，并不能準確地驗證猜想.因此，我們需要經過大量反復的實驗，才能證明結論是否正確.請同學們利用平板電腦模擬實驗，增加實驗的次數，觀察硬幣正面朝上的頻率會有什么樣的變化？

模擬實驗：請在平板電腦上輸入拋擲硬幣的次數，觀察硬幣出現正面朝上的頻率.

師：（手機投屏學生實驗的結果）請你們組來說一說增加實驗的次數，硬幣正面朝上的頻率有什么變化？

生：我們輸入的實驗次數從300到幾千，發現得出的頻率越來越接近0.5.

師：為進一步觀察拋擲硬幣次數與拋得硬幣正面朝上次數的關系，請你利用幾何畫板進行大量的實驗，觀察隨著試驗次數的增加，硬幣正面朝上的頻率將會有什么變化？

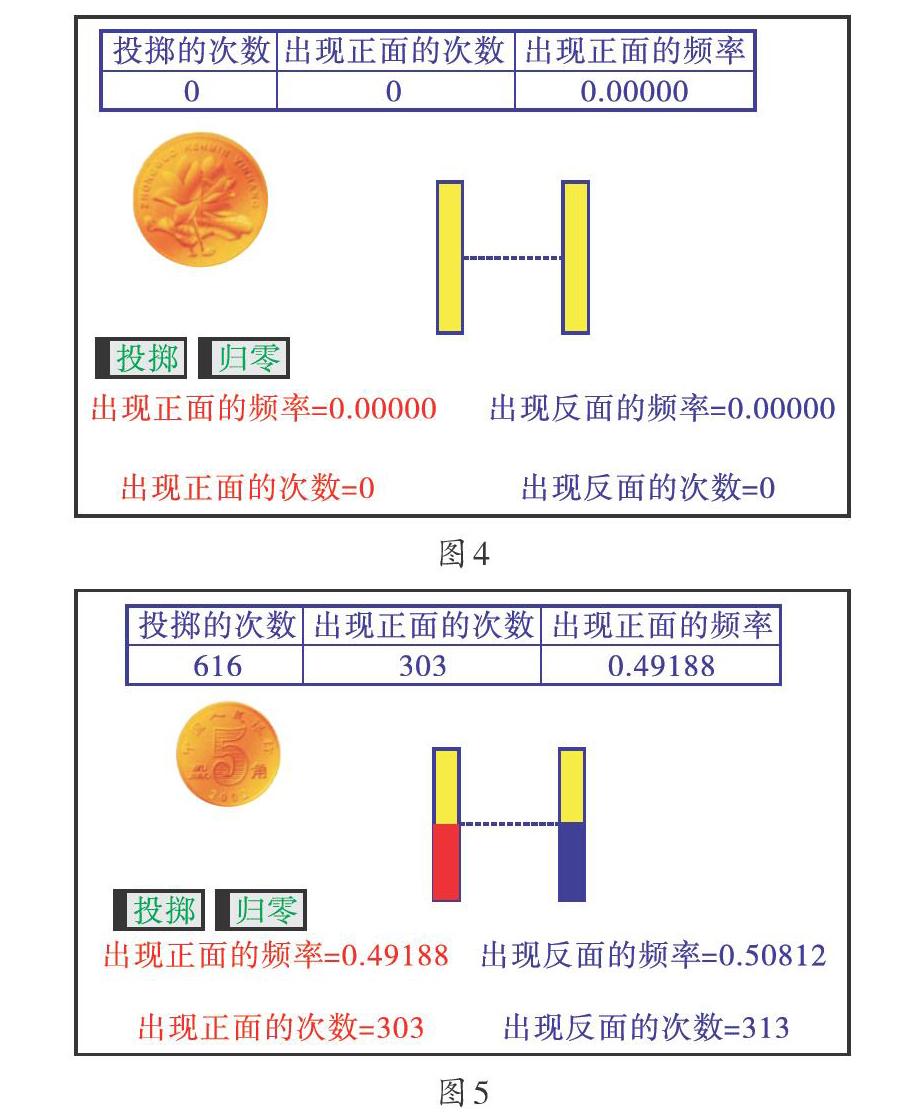
幾何畫板模擬實驗：圖4是老師利用幾何畫板演示的初始狀態，圖5是幾何畫板演示的部分結果.

生：我發現剛開始硬幣正面朝上的頻率波動幅度很大，有起有落，隨著實驗次數的增加，硬幣正面朝上的頻率越來越穩定，趨向于0.5，并且在0.5附近波動的幅度越來越小.

師：從這里我們可以知道，概率針對大量重復實驗而言，大量的重復的實驗體現的規律并非在每一次試驗中都會發生，所以，拋擲一枚質地均勻的硬幣，正面朝上的概率是0.5，并不意味著拋擲20次硬幣，一定會有10次正面朝上.

【評析】執教老師讓學生開展拋擲硬幣的隨機試驗，嘗試收集數據和描述數據，再次體會隨機事件概率的意義，培養學生的隨機觀念.借助H5模擬拋擲硬幣動畫和幾何畫板，可以將硬幣正面朝上與反面朝上的頻率波動性與穩定性直觀地呈現出來，信息技術的介入適時、適度、有效.

五、課堂小結，能力提升

師：這節課你的收獲是什么？

生1：我知道概率的概念和求概率的計算公式.

生2：概率針對大量的重復的試驗而言，當某一件事的頻率波動穩定在某一個數值時，可以估計成這個事件的概率.

生3：我知道抽獎游戲是如何設計的，中獎率完全可以因人設計，所以，不能盲目地相信手機上小程序發送的抽獎游戲.

師：這節課也讓我們知道，任何一個實驗猜想都需要大量的實驗去驗證.在信息技術飛速發展的時代，可以巧妙地利用信息技術幫助我們解決生活中的問題.

師：請同學們完成以下習題.

1.判斷下列說法是否正確.

（1）不可能事件發生的概率為0.

（2）某種彩票中獎概率為1%，買100張彩票一定有1張中獎.

2.擲一枚質地均勻的骰子，觀察向上一面的點數，點數為奇數的概率是? ? .

3.在一個游戲轉盤中，紅、黃、藍三個扇形的圓心角度數分別為60°，90°，210°，讓轉盤自由轉動，指針停止后落在黃色區域的概率是? ? .

A.[16]? ?B.[14]? ?C.[13]? ?D.[712]

4.小組設計一個總數為24人的抽獎小游戲，每人抽一次，要求：一等獎的概率是[124]，二等獎的概率是[112]，三等獎的概率是[16].

師：概率不僅出現在我們的練習題中，生活中也很常見，如幸運大轉盤、刮刮樂等抽獎游戲.請同學們以小組為單位，設計一個總數為24人的抽獎游戲，按照要求計算獲獎人數，看誰能抽中一等獎.

師：請同學們分小組，利用網絡查找概率在生活中有哪些應用，并跟身邊的同學、朋友一起分享.

【評析】在梳理本課所學知識時，執教老師通過習題檢測，檢查學生達成學習目標的情況.知識的拓展與延伸，讓學生真實地感受到數學源于生活，同時也服務于生活.

【總評】

執教老師在教學人教版數學九年級上冊《隨機事件與概率》過程中，結合真實情景中的案例，幫助學生理解概率的概念，啟發學生歸納概率的計算公式，學會用公式計算概率，有效地落實了數學課標對這一教學內容的要求.這節課亮點比較多，主要體現在四個方面.

第一，重視隨機觀念的培養.隨機觀念的培養是初中階段統計與概率學習的一項重要內容，執教老師設計了電影票分配、摸球、拋硬幣、抽獎等練習，讓學生在操作中體驗隨機事件的不確定性，深刻理解在大量的重復的實驗中呈現出來的規律性，這是培養學生隨機觀念非常重要的兩個方面.

第二，加強概率意義的理解.學生在小學階段對事件發生可能性的大小已有初步認識，但只限于定性的描述，這節課從具體的實例引導學生從定量的角度刻畫隨機事件發生的可能性大小，總結出一般規律，歸納得出簡單隨機事件的計算公式，有利于學生加深對概率意義的理解，同時也滲透了從一般到特殊的數學思想.

第三，緊密聯系生活實際.這節課將電影票的分配問題作為教學切入點，設計開放性的問題，說明數學源于生活.在知識的形成過程中，執教老師設計了摸球、拋硬幣等問題，培養了學生的抽象能力，在應用概率公式解決抽獎等問題過程中，讓學生體會到概率與生活實際密切相關，提高了學生應用知識解決問題的能力.

第四，注重信息技術的應用.執教老師從學生自主設計游戲開始引入教學，善于將信息技術與教學相融合，同屏展示學生設計的方案及時有效.利用H5動畫完成拖球游戲，同屏展示各小組實驗結果，讓學生分享和交流想法，發展了學生的思維.學生小組合作完成拋硬幣實驗后，執教老師借助H5動畫和幾何畫板模擬實驗，減少了課堂實驗時間，并且把硬幣正面朝上與反面朝上的頻率波動性與穩定性直觀地呈現出來，更好地突破了教學難點.

注：本課例在2019年第17屆全國初中信息技術與教學融合創新同課異構觀摩課中獲一等獎.

（責編 歐孔群）