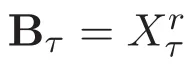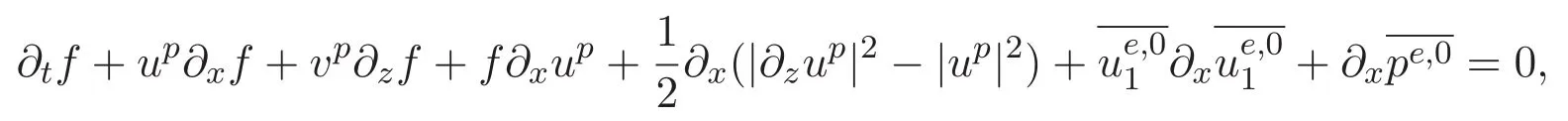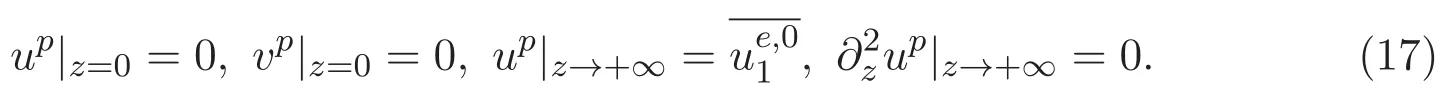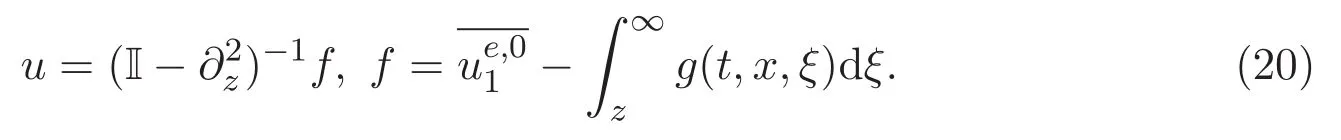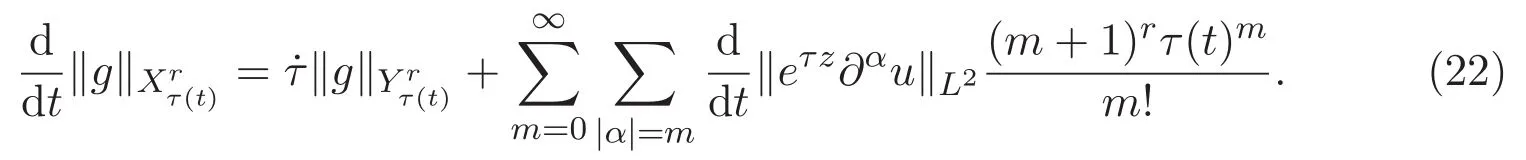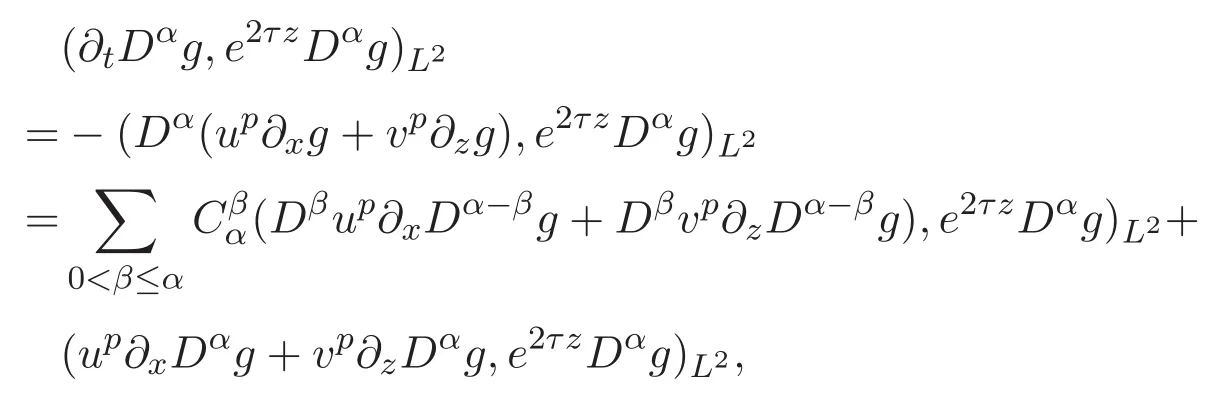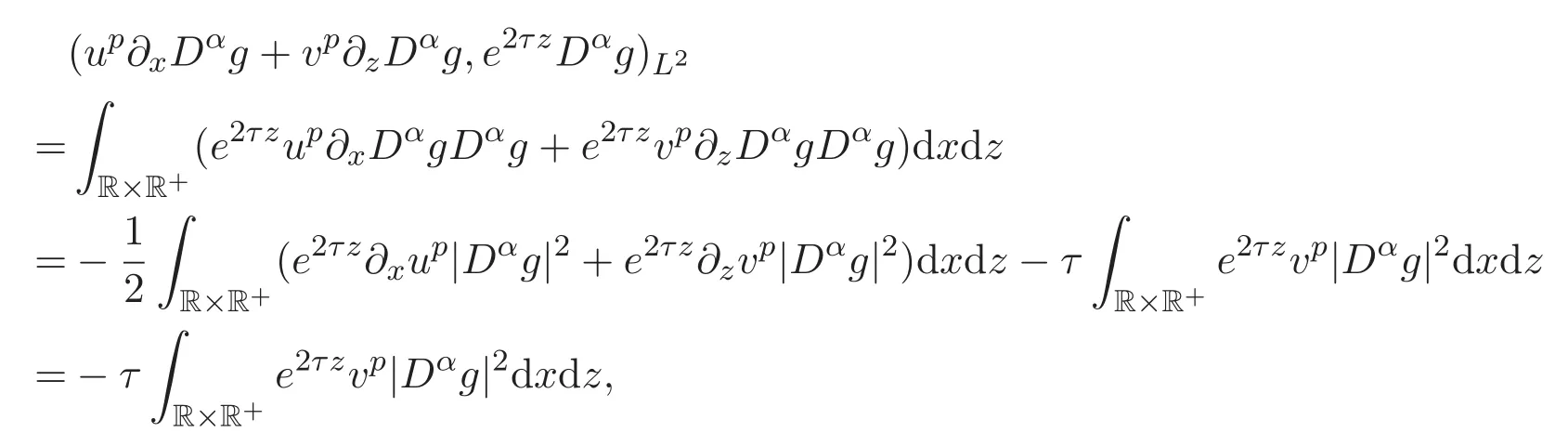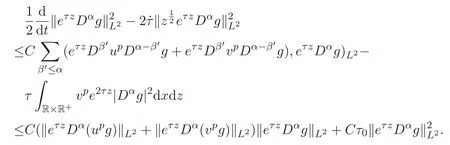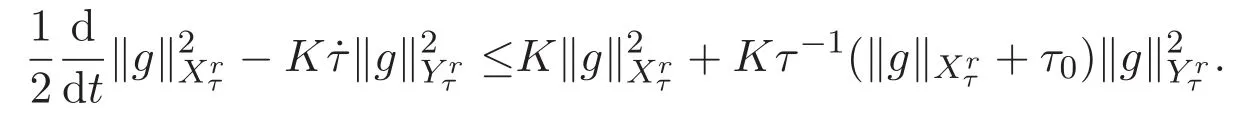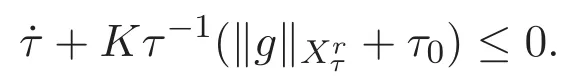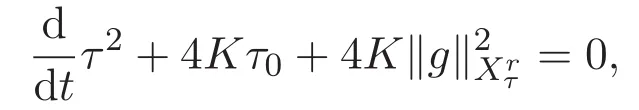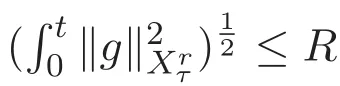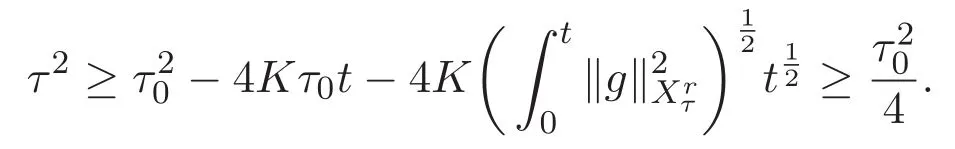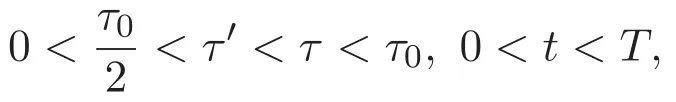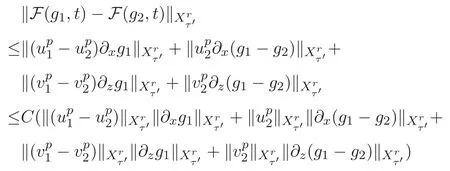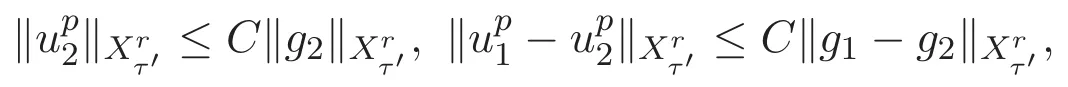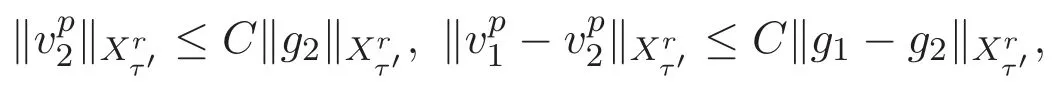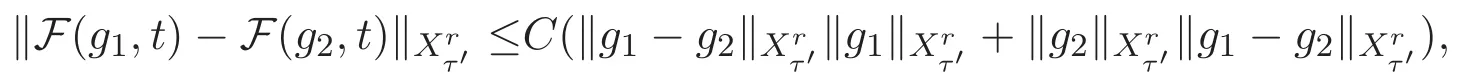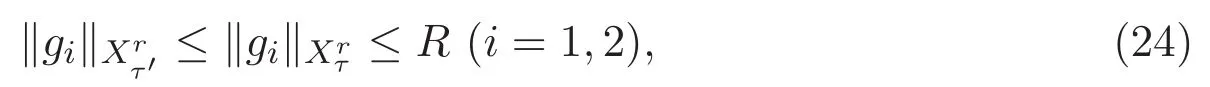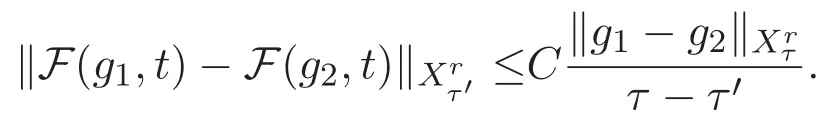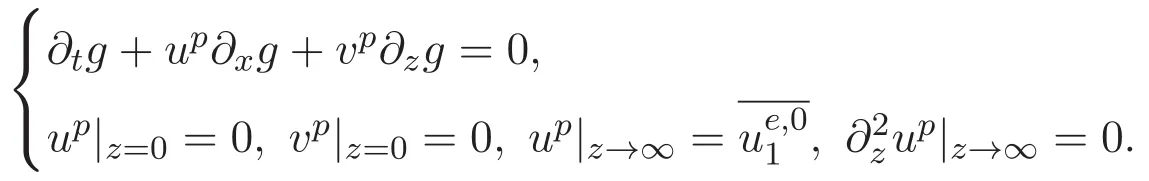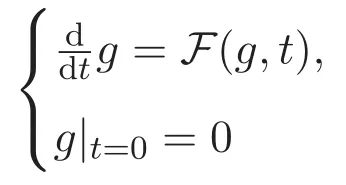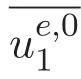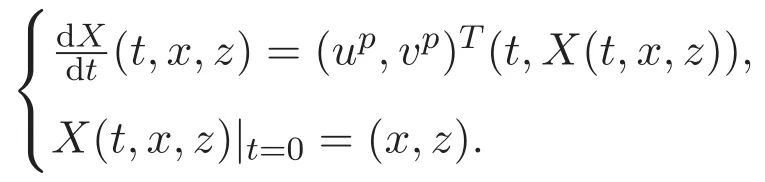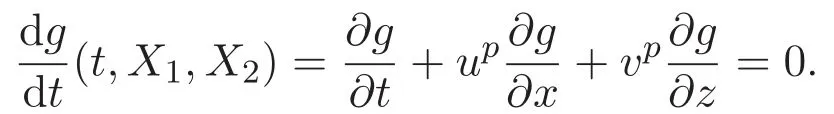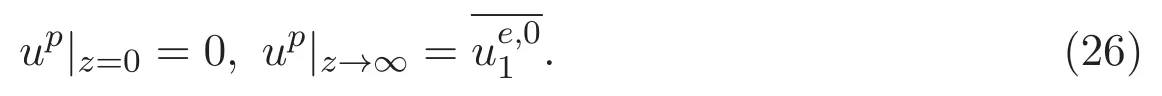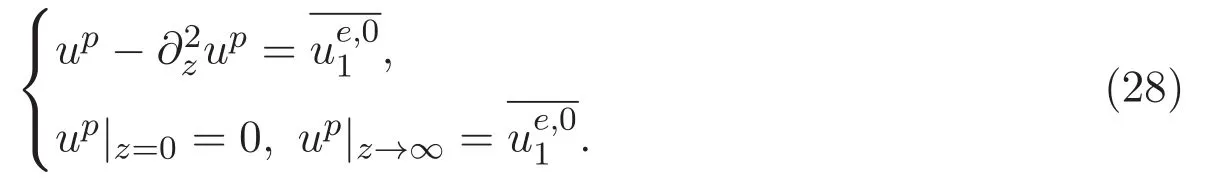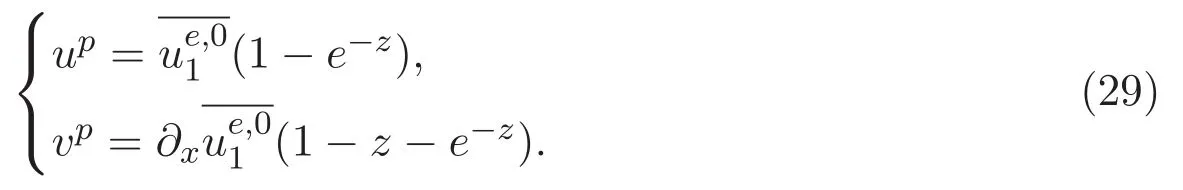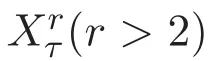半平面上Euler-α方程組的邊界層方程整體適定性
孫小梅,臧愛彬
(1.西北大學數學學院,陜西 西安 710127)
(2.宜春學院數學與計算機科學學院和宜春學院應用數學研究中心,江西 宜春 336000)
1 引言
在半平面上具有Dirichlet邊界條件的Euler-α方程組有如下描述
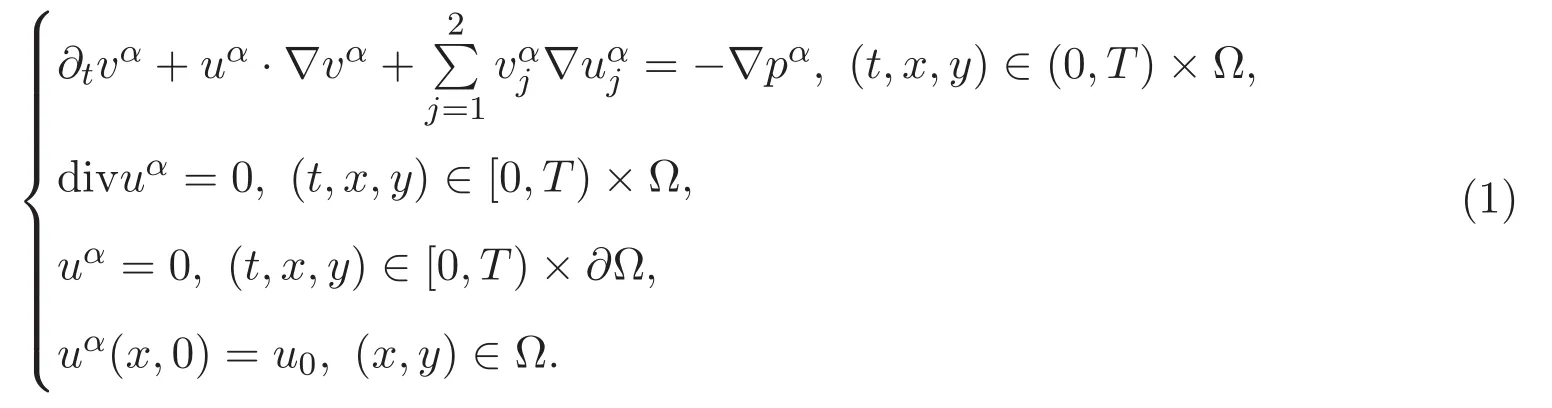
文獻 [2]通過使用幾何工具證明了初始值u0∈Hs(?)(s>2)時問題 (1)的存在唯一性.文獻[3]用描述粒子演化的唯一拉格朗日流圖證明了Radon測度空間中具有初始渦量的二維Euler-α方程組整體弱解的存在唯一性.對于足夠光滑的初始數據,文獻[4]證明了Euler-α方程組存在唯一局部強解,并證明了二維情況下Euler-α方程組具有整體唯一強解.
形式上,令方程組(1)中的參數α=0,可以得到Euler方程組的初邊值問題
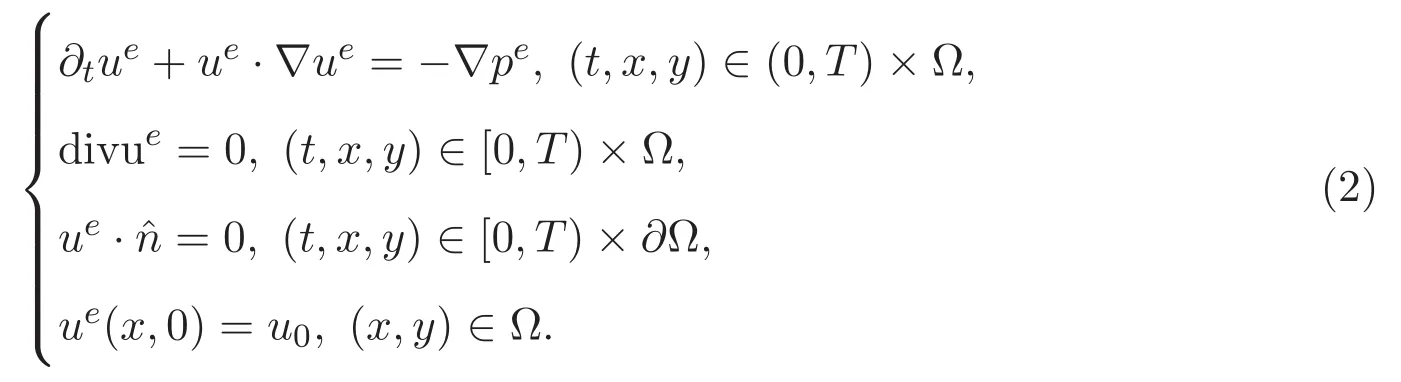
對于Euler方程組的適定性已經有了廣泛的研究,文獻[5]證明了n維區域內Euler方程組(2)經典解的局部存在唯一性,而在二維情形下該解還是整體存在的,更多細節讀者可參考文獻[6].
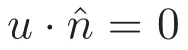
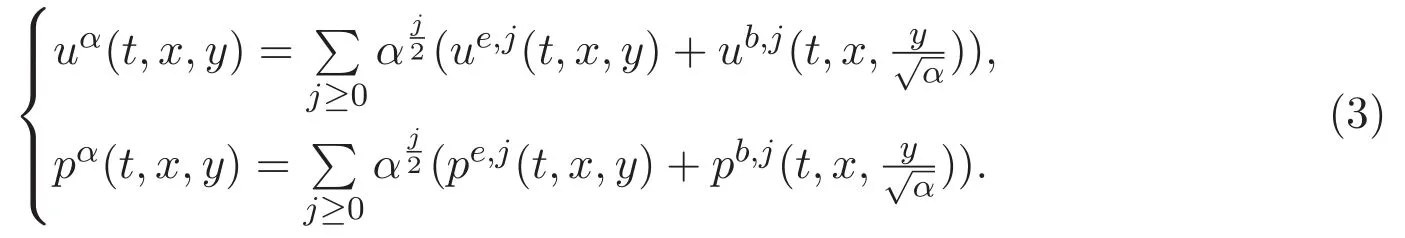
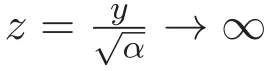
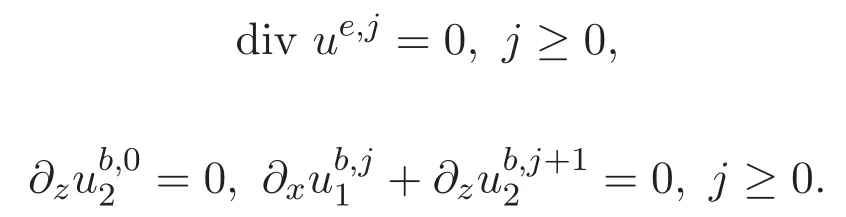

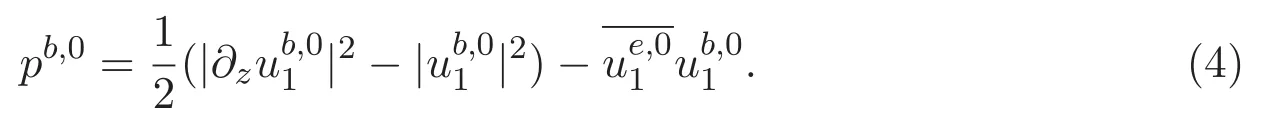
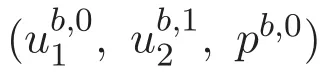
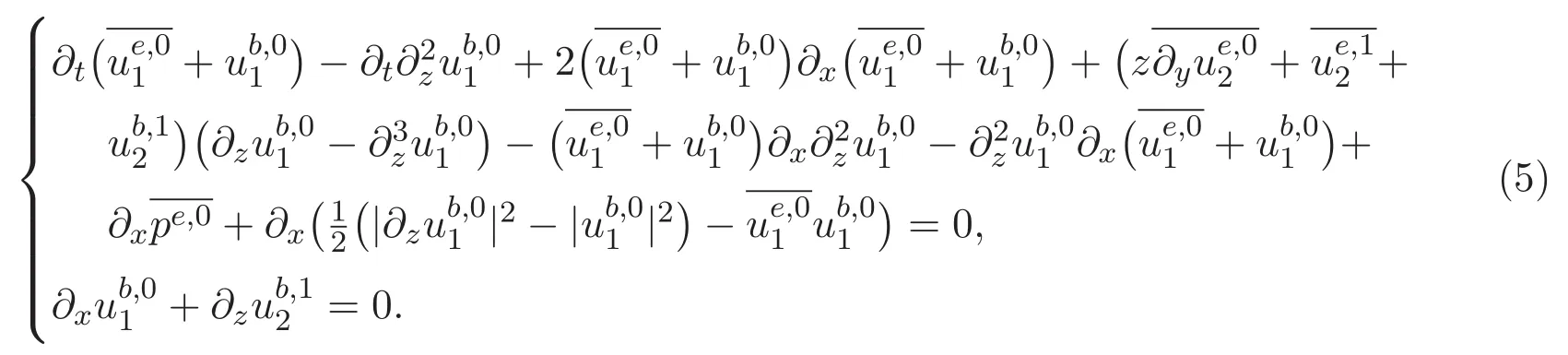
以及邊界條件

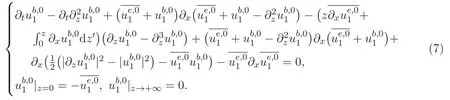
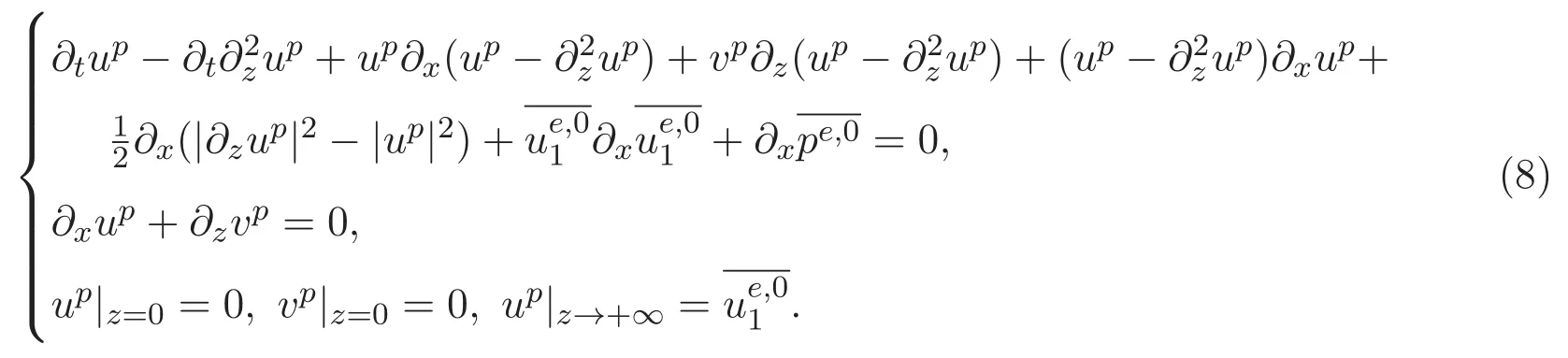
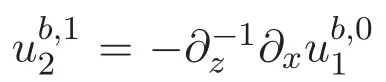
本文的主要內容結構如下:第二部分給出了加權Lebesgue-Sobolev函數空間以及解析函數空間族的定義及性質.簡述了ACK定理的內容和證明一些有用的命題.最后部分通過構造邊界層方程組的等價形式,引入了兩個技術性的引理,從而給出本文的主要結論及證明.
2 符號及預備知識
為方便起見,對于正數r,τ>0,定義以下的加權Lebesgue函數空間
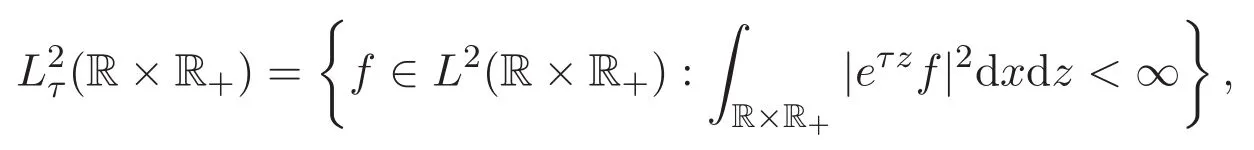
以及加權的Sobolev函數空間
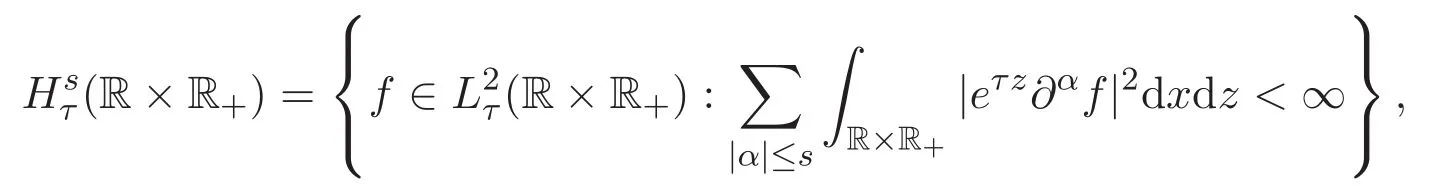
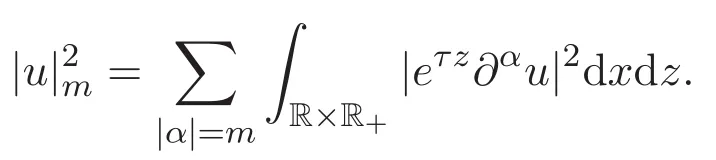
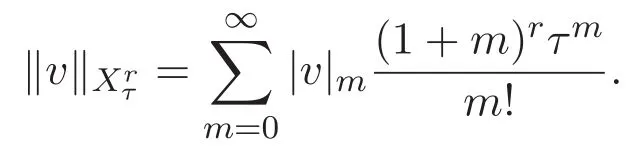
并記
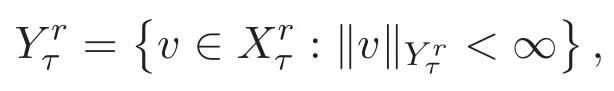
具有范數
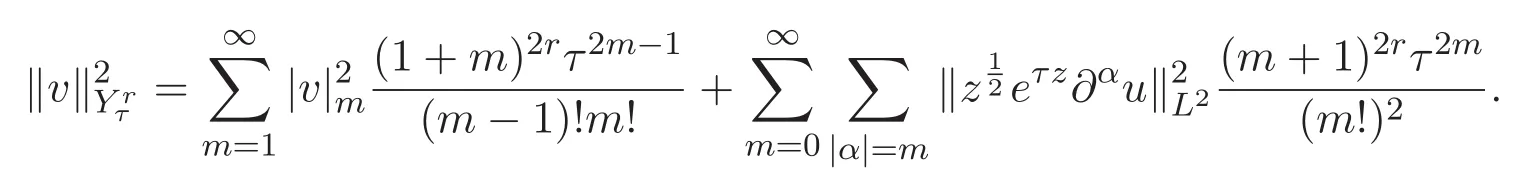
本文還需要利用到下列單變量實解析函數空間
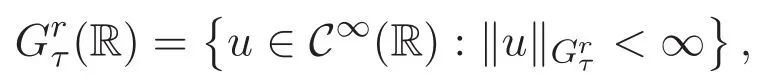
以及
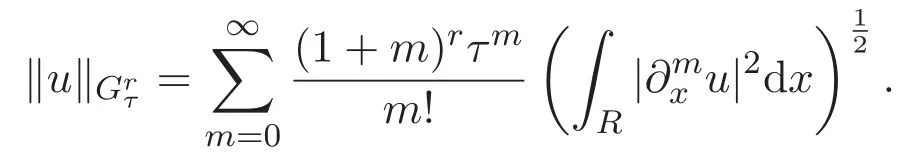
性質 2.1 設 0<τ′<τ,則有

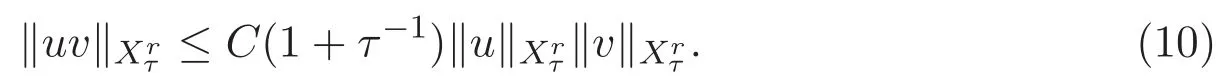
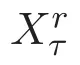
ACK 定理[14]設 {Bs:0 其中C不依賴于s,s′,t,u,v.此外F(0,t)∈Bs在(0,T)是連續的且存在固定常數K,使得‖F(0,t)‖s≤K.則對于 0 存在唯一解 u(t)∈Bs,0 對可測函數f,考慮下列方程 其中C>0不依賴于u,f. 利用分部積分有 從而 利用插值不等式有 由數學歸納法知對任意k≥0有 對上式關于 z 求偏導可化為 ?t?zf+up?x?zf+vp?z?zf=0,記 g=?zf,則有 對應的邊界條件 令 故得到了與方程組(8)同解的微分方程組 以及 為了驗證邊界層方程滿足ACK定理的條件,需要證明下面兩個引理. 證明 不妨設解析半徑τ是關于t單調遞減足夠快的函數,從而有 考慮邊界層方程組(8)的等價形式 對上式的方程兩端作用微分算子Dα,并關于e2τzDαg做L2內積,可以得到 其中 從而 利用文獻[16]的計算方法,而u由方程組(20)決定,利用命題3.3的結論及不可壓性質,則有 求解常微分方程得 引理 3.2 設F如(18)式定義,在與引理3.1的假設下,則對于 上面估計的最后一步運用了解析函數的性質2.2,又根據命題2.3有 同理由于散度為零,從而 故有 其中 由條件知 結合(23)-(24)式可得 下面給出本文的主要結論. 證明 考慮邊界層方程組(8)的等價形式 首先定義空間 則 另一方面,在上述條件下設(X1,X2)滿足 則 因此對任意t>0,g(t,X1,X2)=g(t,X1,X2)|t=0=0,故有 滿足邊界條件 從而 結合(25)-(27)式可得 解常微分方程(28)可得 注:臧愛彬為孫小梅聯合導師.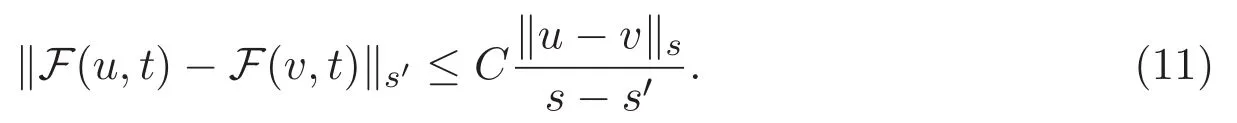
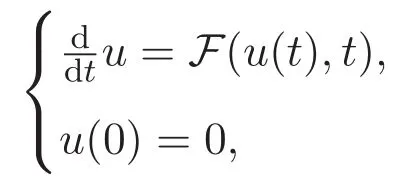
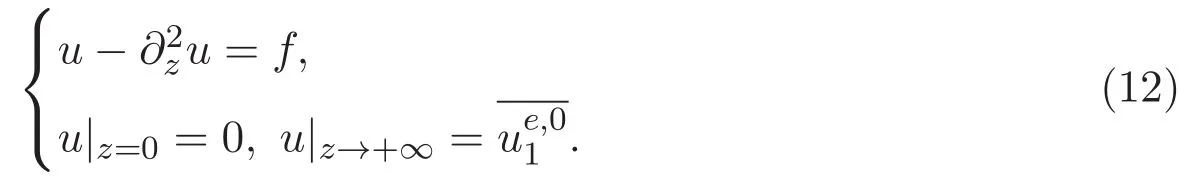
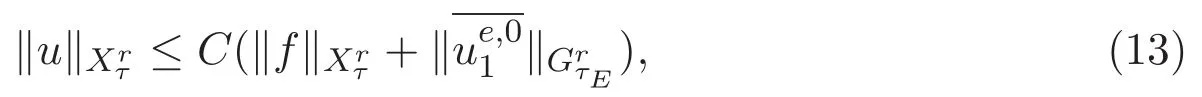

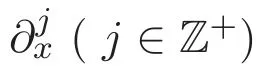
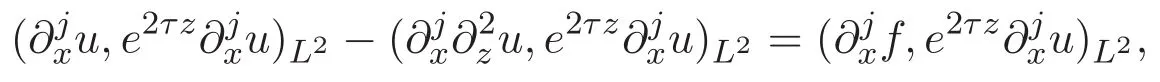
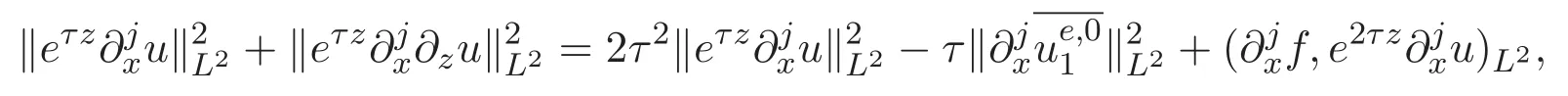
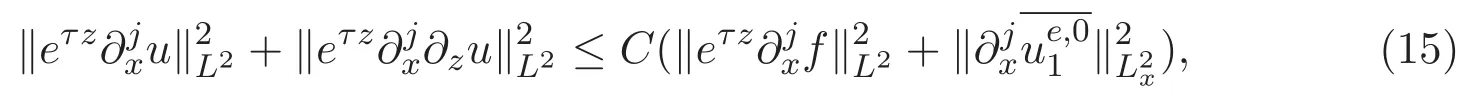
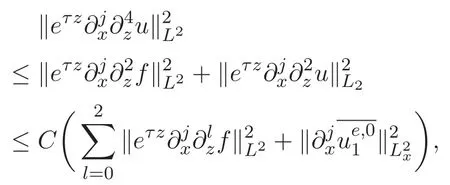
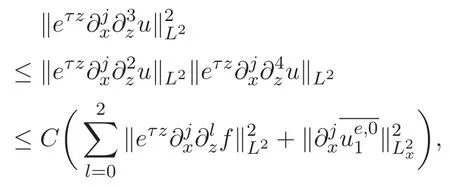
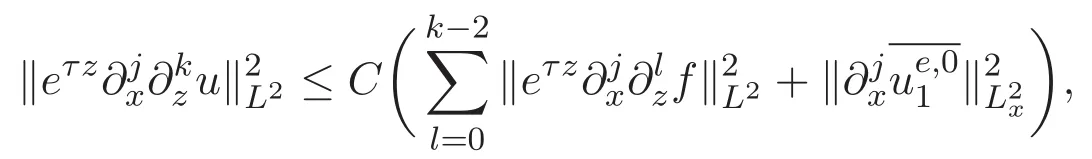
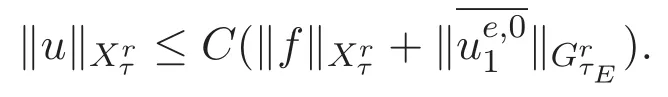
3 主要結論及證明