Koch曲線的Hausdorff測度上界的研究
郭東亮,李聰端,秦家銀
(1.中山大學電子與通信工程學院,廣東 深圳 518107;2.中山大學電子與信息工程學院,廣東 廣州 510006)
1 引言
在分形幾何研究中,分形的Hausdorff維數與Hausdorff測度的確定很重要,但又是一個難題,二者中Hausdorff測度的計算更加困難[1-5].計算一般集合的Hausdorff測度難度很大,不存在普遍適用的方法.滿足開集條件的自相似分形集由于具有嚴格的自相似性,在計算Hausdorff測度方面的研究成果最多.Cantor集,Koch曲線和Sierpinski墊片是3個經典的自相似集,目前三分Cantor集的Hausdorff維數與Hausdorff測度已經得到完全解決[1],但對于Koch曲線和Sierpinski墊片,人們只求出其Hausdorff維數,Hausdorff測度則難以給出準確值,只能估計其上下界[2-4].
文獻[2-3,6-8]均研究了Koch曲線的Hausdorff測度并對其上界進行了估計,文獻[9]利用數值計算方法研究了Koch曲線的Hausdorff測度的上界估計值.在已公開發表的文獻中,Koch曲線的Hausdorff測度的最好上界是Hs(K)≤0.587697.
本文在已有研究成果基礎上,通過在Koch曲線上構造分形級更高的新覆蓋并利用相關定理,得出Koch曲線Hausdorff測度的更好上界估計Hs(K)≤0.58764947,并通過進一步的分析,給出了Koch曲線的Hausdorff測度的精確上界在0.58764946至0.58764947之間.
2 Koch曲線及其Hausdorff測度

下面是關于Koch曲線K的一些相關定義和結果[1-2].
(2)設n≥1,Kn中夾角為60?的相鄰兩邊構成一個正三角形,稱作Kn的基本三角形,并記作?n;
(3)K 是路徑連通的,設點A,A′∈K,記AA′為K 上的從點A到點A′的連通弧;
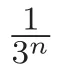
Hausdorff測度記為Hs(·),本文中使用如下引理:
引理 2.1[1]由Hausdorff測度的齊次性知
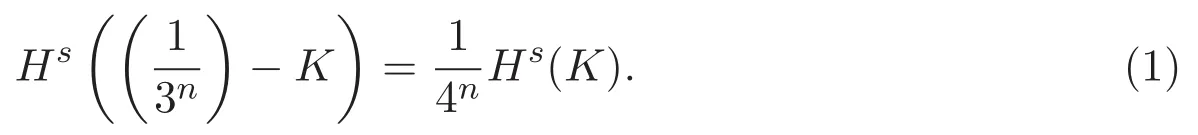
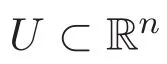

3 已有結果分析
將圖1的FB段圖形放大,得到圖2,在屬于K4的邊FB上生成屬于K5的正三角形?GHI,再在屬于K5的邊GB上生成屬于K6的正三角形?JLM,文獻[6]和文獻 [7]分別將九邊形 JMDEOE′D′M′J′作為新覆蓋(M′,J′分別為 M,J關于直線OO′的對稱點),基于K6上的連通弧MM′,推導出了K 的Hausdorff測度的更好上界估計值Hs(K)≤0.587847293.
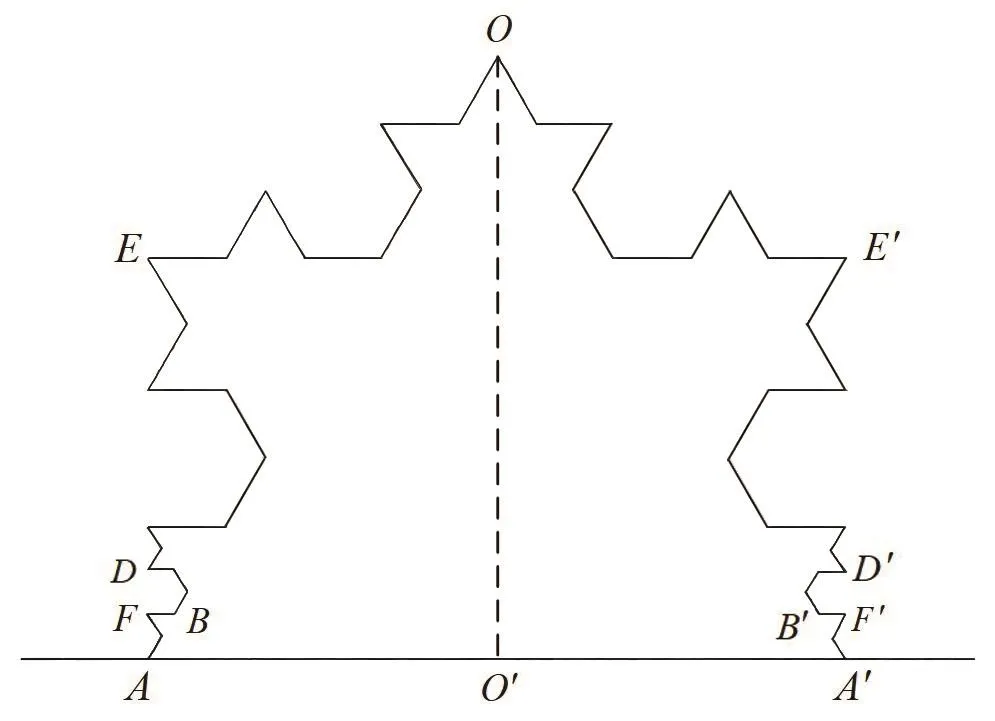
圖1 Koch曲線局部示意圖(迭代至K4)
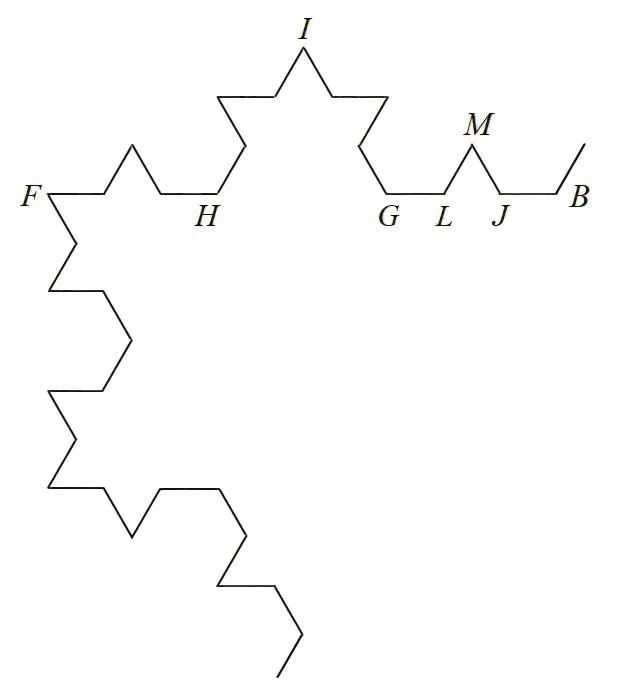
圖2 圖1的FB段圖形(迭代至K6)
繼續放大圖 2中 LMJB段圖形,得到圖 3,其中正三角形 ?NPQ屬于 K7,文獻 [8]基于 K7構造七邊形新覆蓋而將 K的 Hausdorff測度上界進一步減小至Hs(K)≤0.587697,這是已公開發表的文獻中Koch曲線的Hausdorff測度的最好上界.
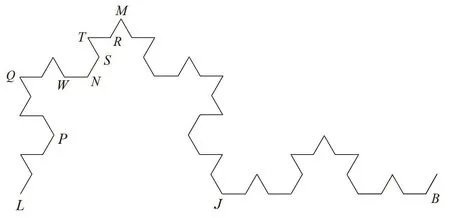
圖3 圖2的LMJB段圖形(迭代至K8)
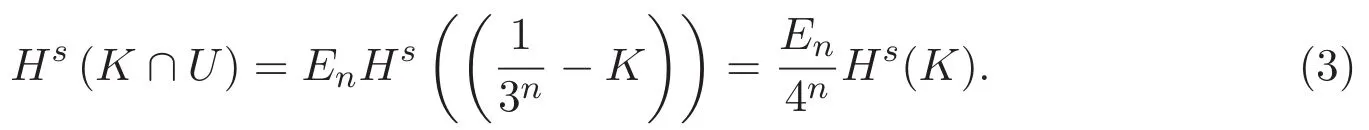
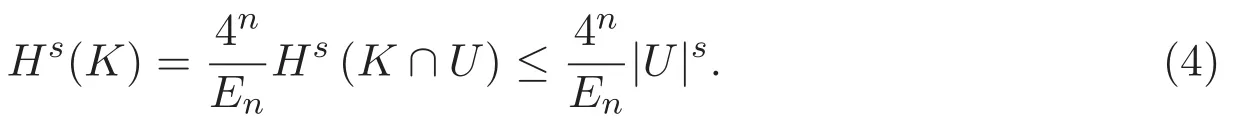

表1 比值μ與分形級數n
由表 1可知,μ隨著 n的增加而降低并趨于收斂.本文基于這一規律分別在K10,K12,K14這些更高的分形級上構造新覆蓋,進一步改進Koch曲線的Hausdorff測度上界.
4 主要結果及證明
將Koch曲線K迭代至K10,可得到定理4.1.
定理 4.1 Koch曲線表示為K,則K的Hausdorff測度的上界

證明 在圖 3中,正三角形?RST屬于K8,繼續放大邊WNS段的圖形,得到圖 4,其中正三角形?XY Z屬于K10,將15邊形BJNXZDEOE′D′Z′X′N′J′B′作為新覆蓋 (N′,X′,Z′分別為 N,X,Z關于直線 OO′的對稱點),記為U,并考慮K上的連通弧ZZ′,易見 K∩U=ZZ′.
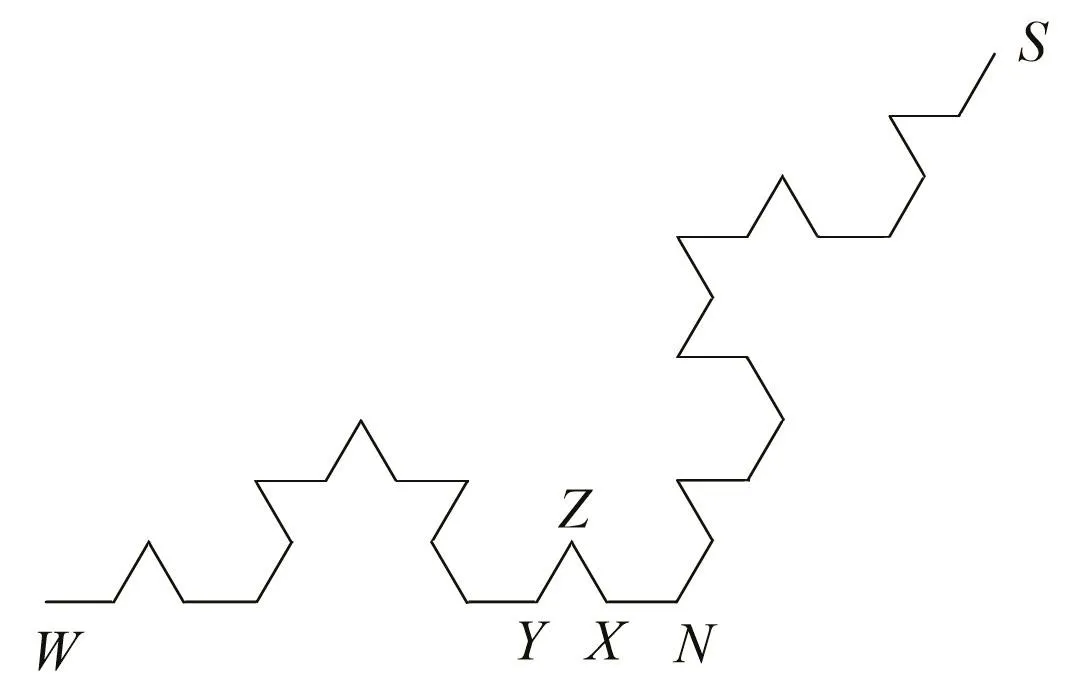
圖4 圖3的WNS段圖形(迭代至K10)
計算新覆蓋U的直徑如下:

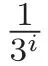
由圖4可以算得
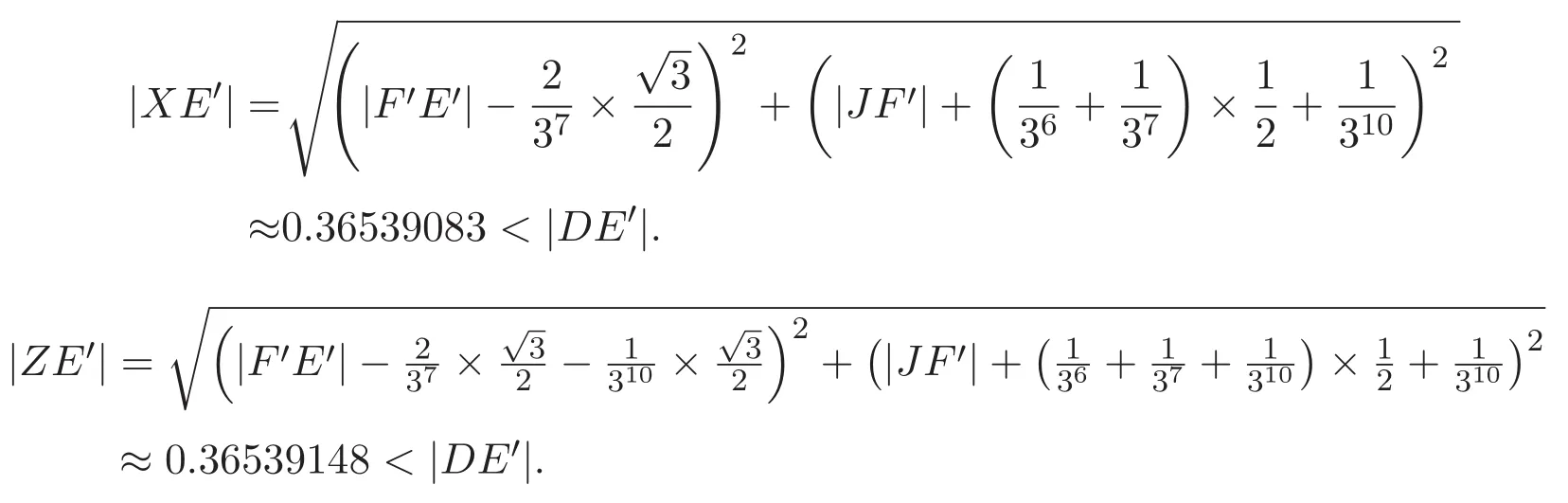
因此,新覆蓋U的直徑是|DE′|.
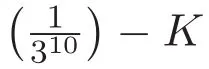
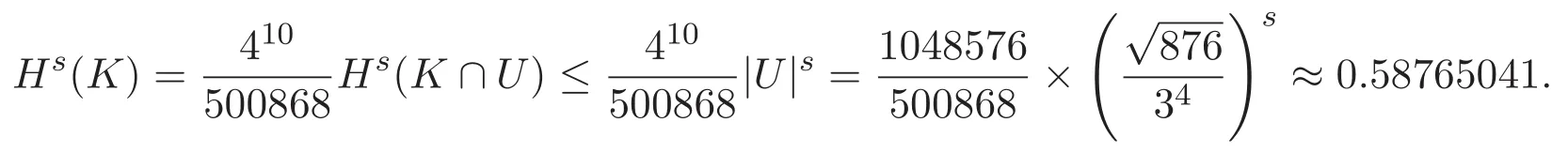
此為迭代至K10時,Koch曲線的Hausdorff測度的上界估計值,該上界已經好于目前已公開發表的最好上界.
放大圖4中的Y Z段,進一步將Koch曲線K迭代至K12,可得到定理4.2.
定理 4.2 Koch曲線表示為K,則K的Hausdorff測度的上界


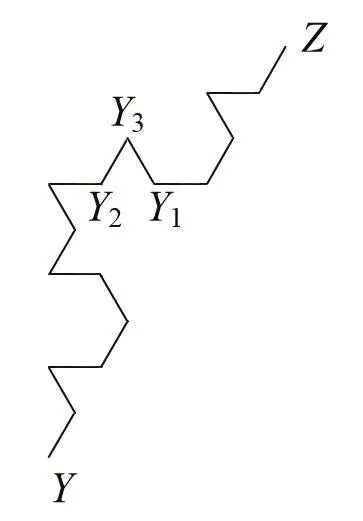
圖5 圖4中Y Z段局部圖形(迭代至K12)
計算新覆蓋U的直徑如下:
直線段Y3E′在水平方向的投影長度為
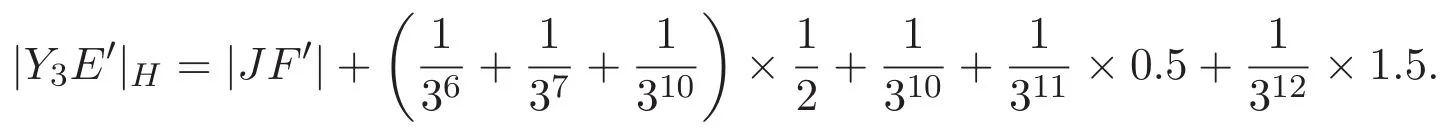
直線段Y3E′在垂直方向的投影長度為
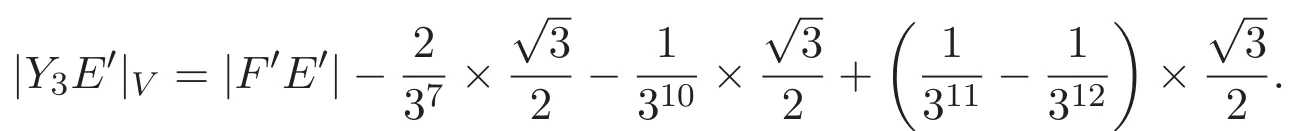
所以,直線段Y3E′的長度為
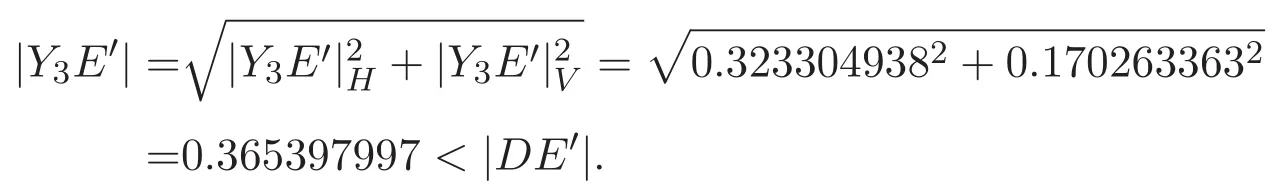
因此,新覆蓋U的直徑仍是|DE′|.
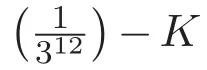
由引理2.2,得

此為迭代至K12時,Koch曲線的Hausdorff測度的上界估計值,該上界好于目前已公開發表的最好上界.
放大圖5中的Y2Y3段,進一步將Koch曲線K 迭代至K14,可得到定理4.3.
定理 4.3 Koch曲線表示為K,則K的Hausdorff測度的上界

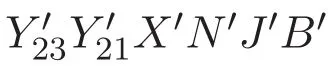
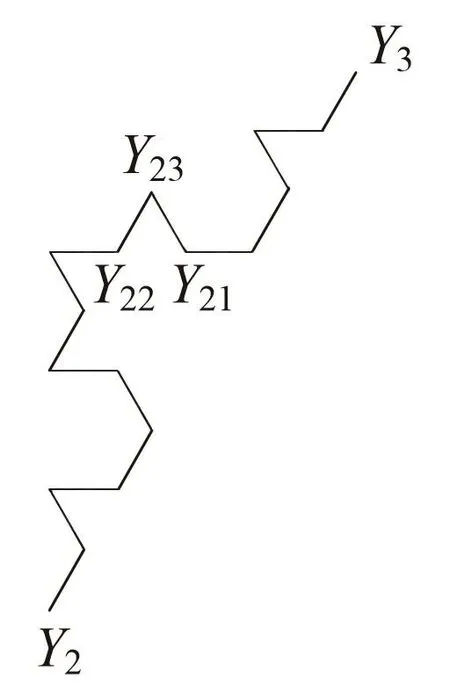
圖6 圖5中Y2Y3段局部圖形(迭代至K14)
計算新覆蓋U的直徑如下:
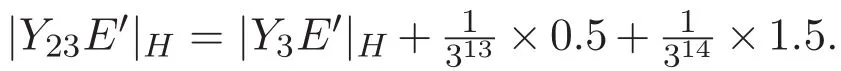
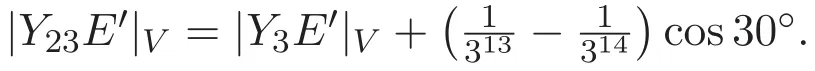
所以,直線段Y23E′的長度為
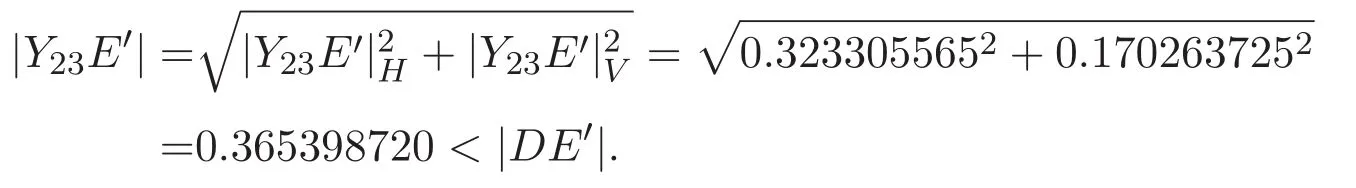
因此,新覆蓋U的直徑仍是|DE′|.
K14∩U共有屬于K14的邊數為
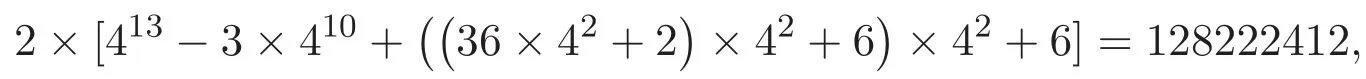
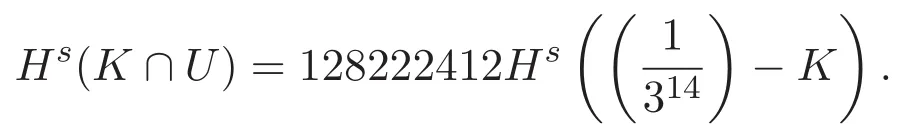
由引理2.1,得
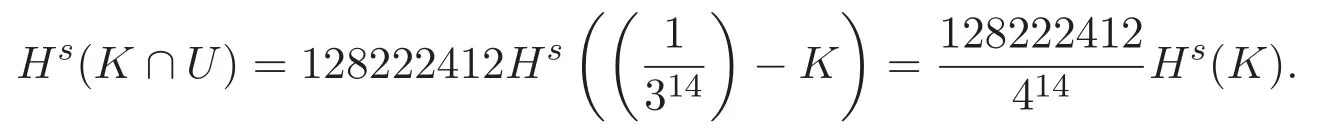
由引理2.2,得
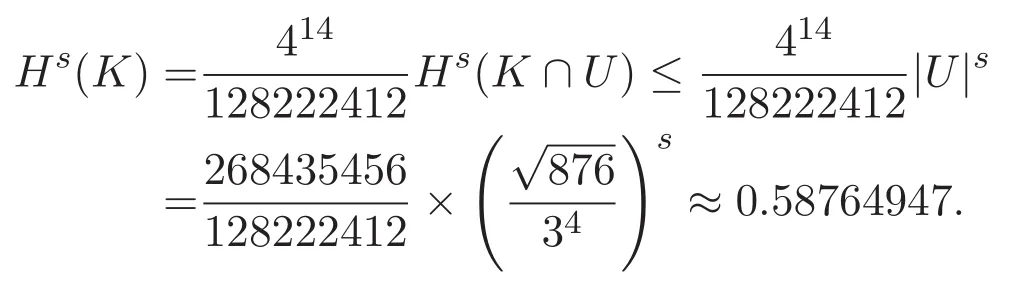
此為迭代至K14時,Koch曲線的Hausdorff測度的上界估計值,該上界好于目前已公開發表的最好上界.
5 經無窮次迭代的上界范圍
設經過無窮次迭代(n→∞),Koch曲線的Hausdorff測度的上界Hs(K)趨于數值 [Hs(K)]?,由圖6知,當迭代至 K14時,若 K 的新覆蓋 U 的直徑是 |DE′|,則在新覆蓋U與K的交集包含最多K14的邊的意義下最優交點是Y23,繼續迭代至超過K14時,若K 的新覆蓋U的直徑仍是|DE′|,易知新覆蓋與K 的交點應位于線段Y22Y23上.因此,[Hs(K)]?的取值范圍是
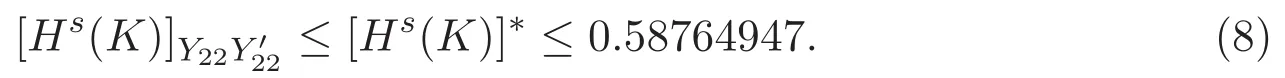
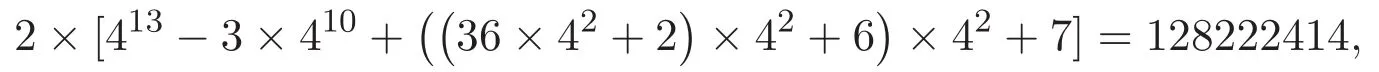
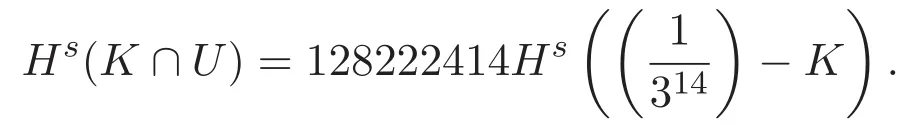
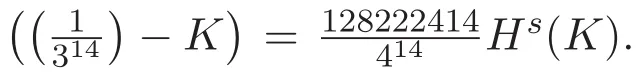
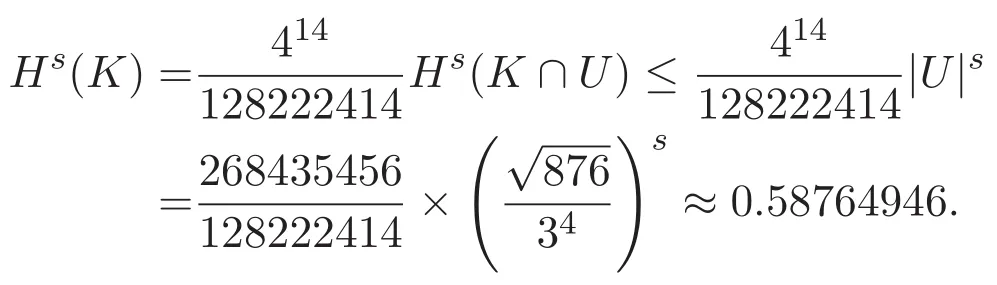
因此,得定理5.1.
定理 5.1 Koch曲線表示為K,則K的Hausdorff測度上界的取值范圍是
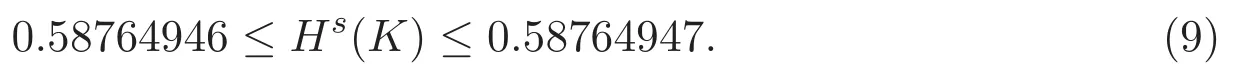
6 結論
本文通過在 Koch曲線的 K10,K12,K14三個更高的分形級上構造更加精細的新覆蓋,利用相關定理計算出了 Koch曲線的 Hausdorff測度的新的上界估計值 Hs(K)≤0.58764947,這是關于 Koch曲線的 Hausdorff測度的迄今所知的最好上界.表 2是文獻中已經發表的和本文新給出的 Koch曲線K的 Hausdorff測度的上界估計值,對應的估計值改進量和絕對誤差限 (K4,K6,K7是文獻中已發表的,K10,K12,K14是本文給出的).
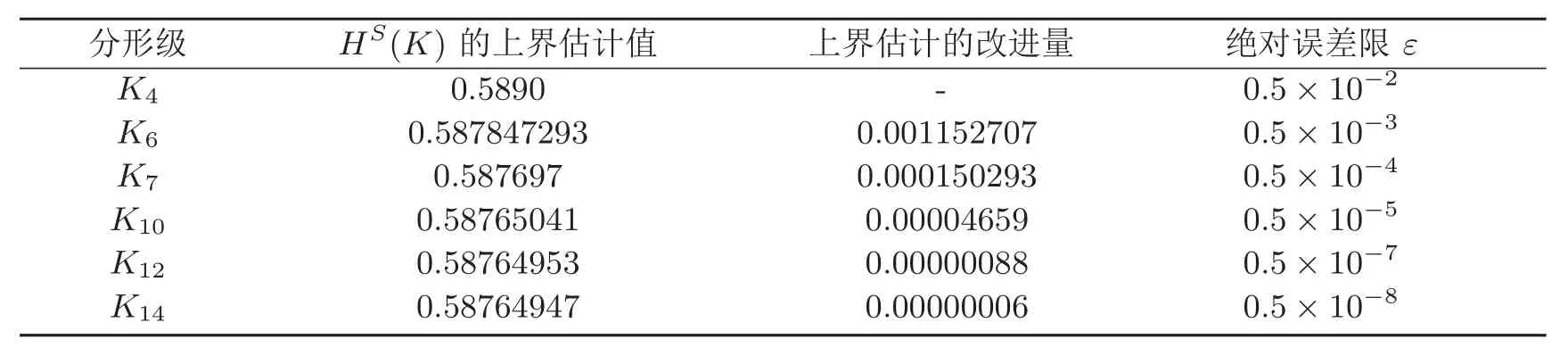
表2 Koch曲線K的Hausdorff測度的上界估計
此外,本文給出 Koch曲線的 Hausdorff測度的上界精確值介于0.58764946和0.58764947之間,由絕對誤差限的相關理論可知:本文給出的上界估計的絕對誤差限為ε≤0.5×10?8.

