三維不可壓縮非牛頓流體/Vlasov方程組的大時間行為

朱歡,方莉

(西北大學數學學院,陜西 西安 710127)

1 引言

本文研究三維周期空間中不可壓縮非牛頓流體/Vlasov方程組的大時間行為,考慮如下方程組

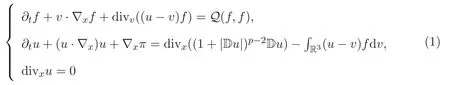
其初始條件為

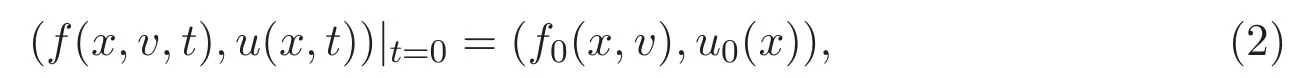
流體-粒子方程組是流體力學中一類重要的模型,常用來模擬流體與粒子的相互作用,由于它在生物學,藥學,石化工業等領域的廣泛應用[1-3],吸引了許多學者的關注.這里簡單介紹流體-粒子耦合模型的相關結果.文獻[4]首次給出不可壓縮Vlasov-Navier-Stokes方程組弱解的全局存在性(N 6 2)和弱解的大時間行為(N=2,3),其中N空間維數.文獻[5]討論了周期區域中不可壓縮Cucker-Smale-Navier-Stokes方程組弱解的全局存在性和時間衰減估計,之后,文獻[6]證明了可壓縮 Cucker-Smale-Navier-Stokes方程組強解的全局存在性,利用Lyapunov函數估計其大時間行為.在文獻[6]的基礎上,文獻[7]介紹了一個新的Lyapunov函數,給出Vlasov-Navier-Stokes系統全局經典解的大時間行為,指出隨著時間的推移粒子與流體速度呈指數衰減.關于流體-粒子方程組的其他結果見文獻[8-9].

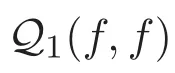
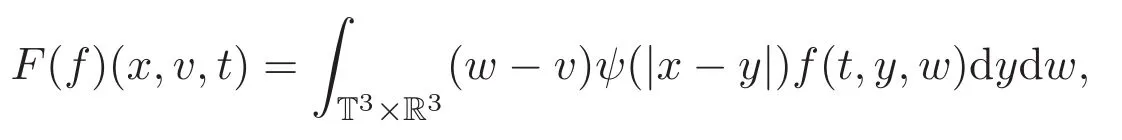
這里ψ(·)是非負,單調不減的光滑對稱函數,研究了該模型三維周期區域中不可壓縮粘性非牛頓流體與Cucker-Smale方程組弱解的存在性并分析了所得解的大時間行為.本文對初始能量提出小性假設,采用文獻[11]中的Lyapunov函數,研究方程組(1)-(2)在三維周期區域下弱解的大時間行為.

首先,定義三維周期空間下的函數空間.

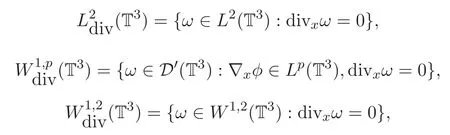
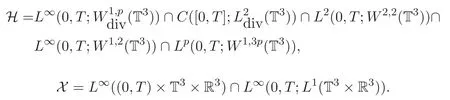
其次,給出方程組(1)-(2)弱解的定義和存在性理論.

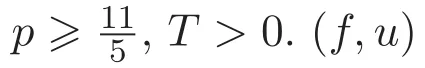
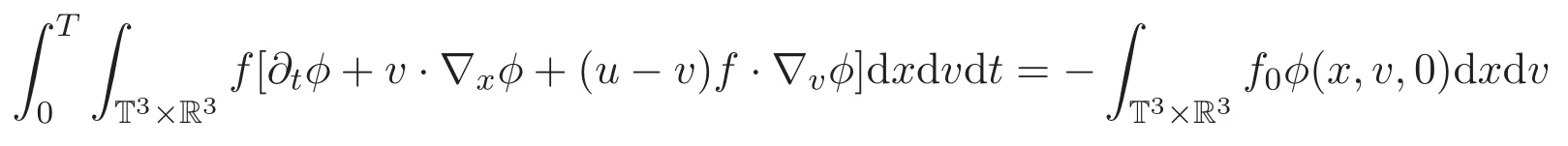
成立.

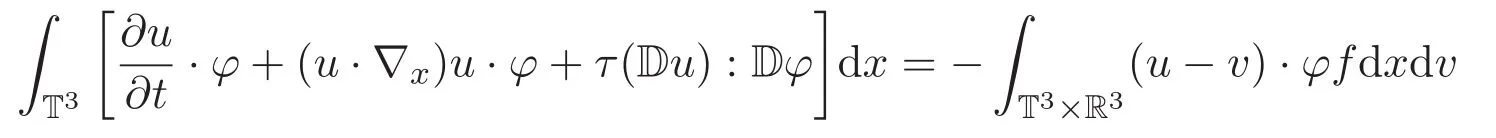
成立.

方程組(1)-(2)弱解的存在性,利用文獻[11]的方法證明可得,本文主要討論該弱解的大時間行為.

接著定義流體與粒子速度變化的平均量,具體如下:

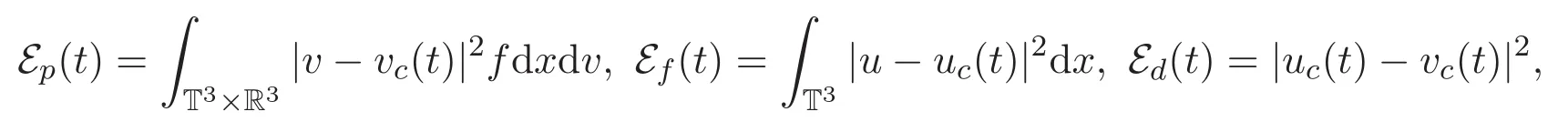
其中

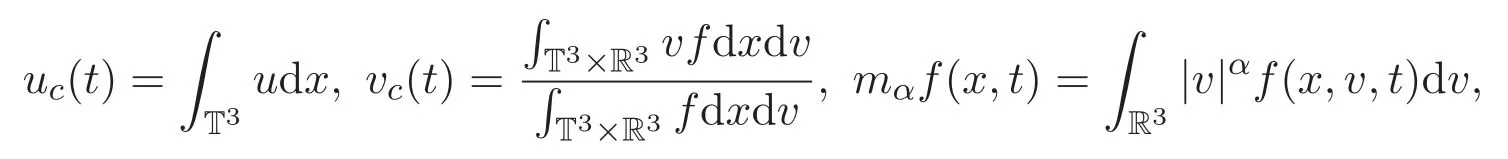
Lyapunov函數E為E(t)=2Ep(t)+2Ef(t)+Ed(t).

最后,闡述本文的主要定理.

定理 1.1 給定T>0.如果(f0,u0),m0f分別滿足

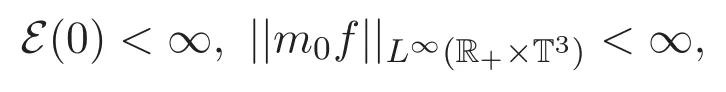
則方程組(1)-(2)弱解的指數估計E(t)6 E(0)e?γt(t∈[0,T))成立,其中

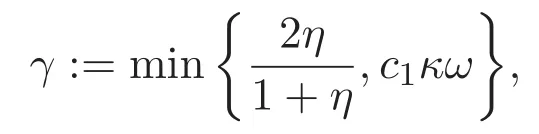
η是不依賴于時間t的正常數且

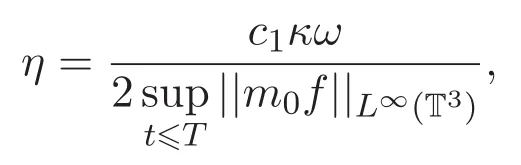
κ和ω分別是三維周期區域Korn′s不等式及Poincare′s不等式中的常數.

2 預備知識

下面給出證明定理1.1必需的兩個引理.

引理 2.1 如果(f,u)是耦合方程組(1)-(2)的弱解滿足

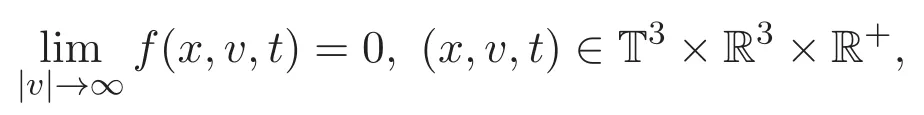
則

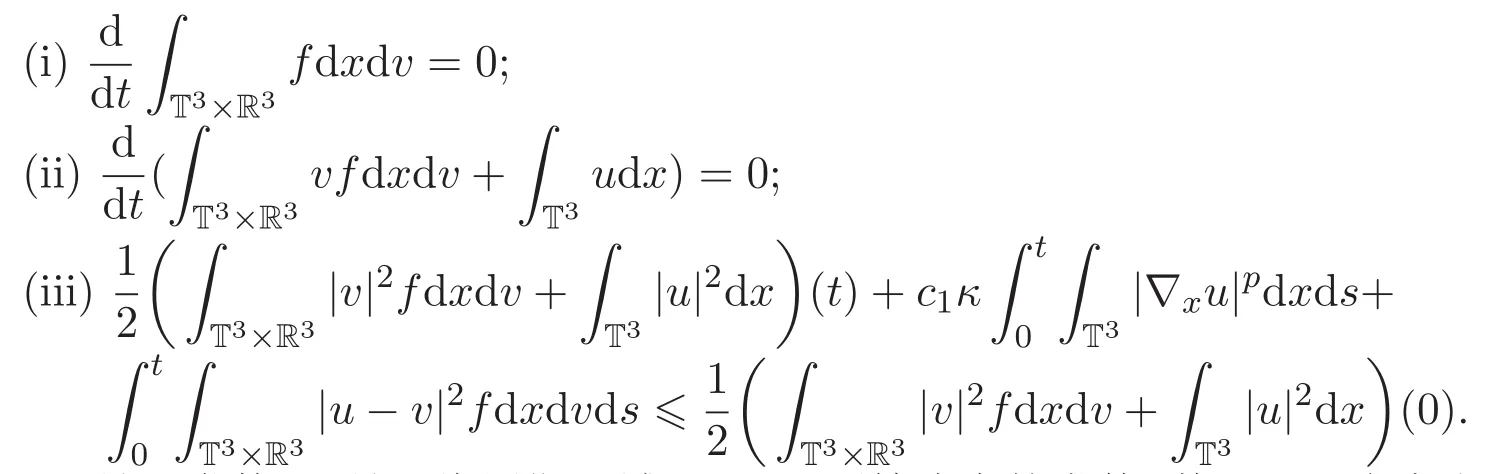
其中c1是正常數,κ是三維周期區域Korn′s不等式中的常數,其證明可參考文獻[8].

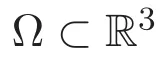
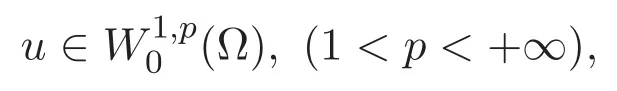
3 定理1.1的證明

為了符號的簡便,記uc=uc(t),vc=vc(t).

引理 3.1 如果(f,u)是耦合方程組(1)-(2)的弱解,則

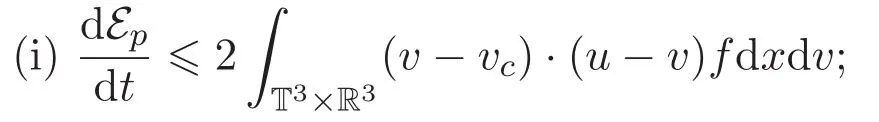
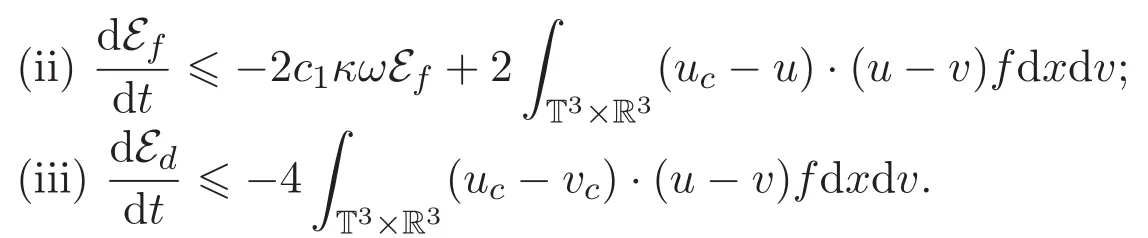
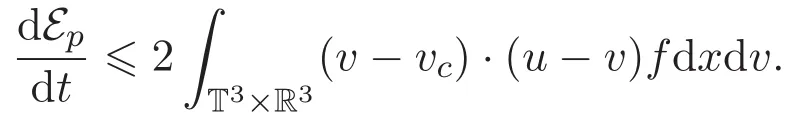
(ii)方程(1)2兩端乘以測試函數(u?uc)且關于x積分可得

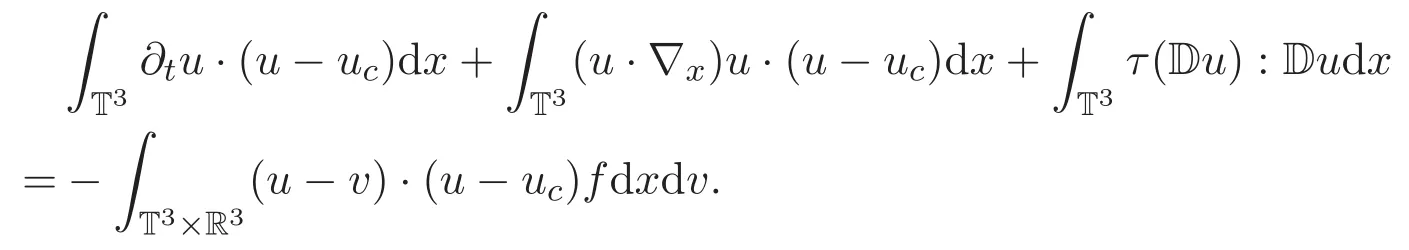
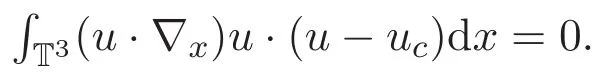
另一方面,利用 Korn′s和 Poincare′s不等式可得

其中κ和ω分別是三維周期區域Korn′s不等式及Poincare′s不等式中的常數,c1為正常數.

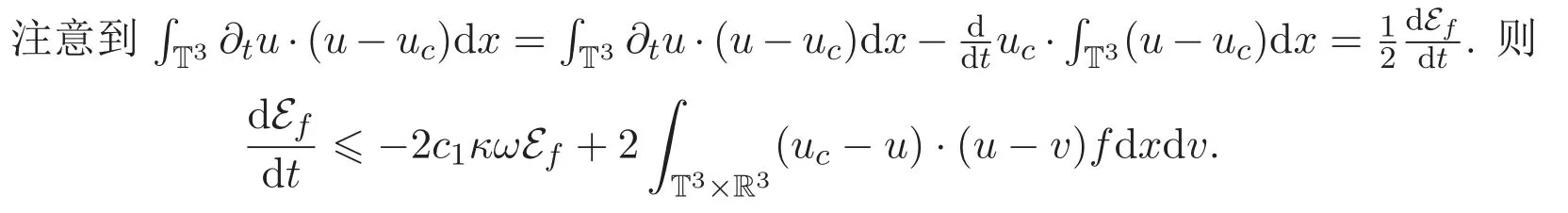
(iii)由引理2.1同理可證.

定理 1.1的證明 注意到E=2Ep+2Ef+Ed,結合引理3.1可得

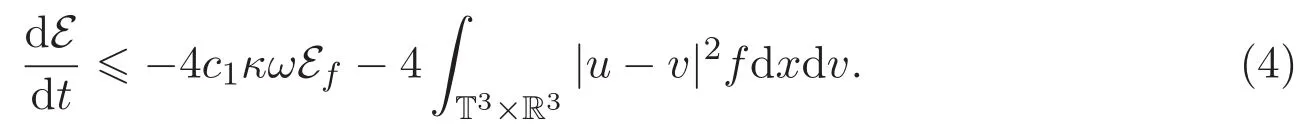
此外

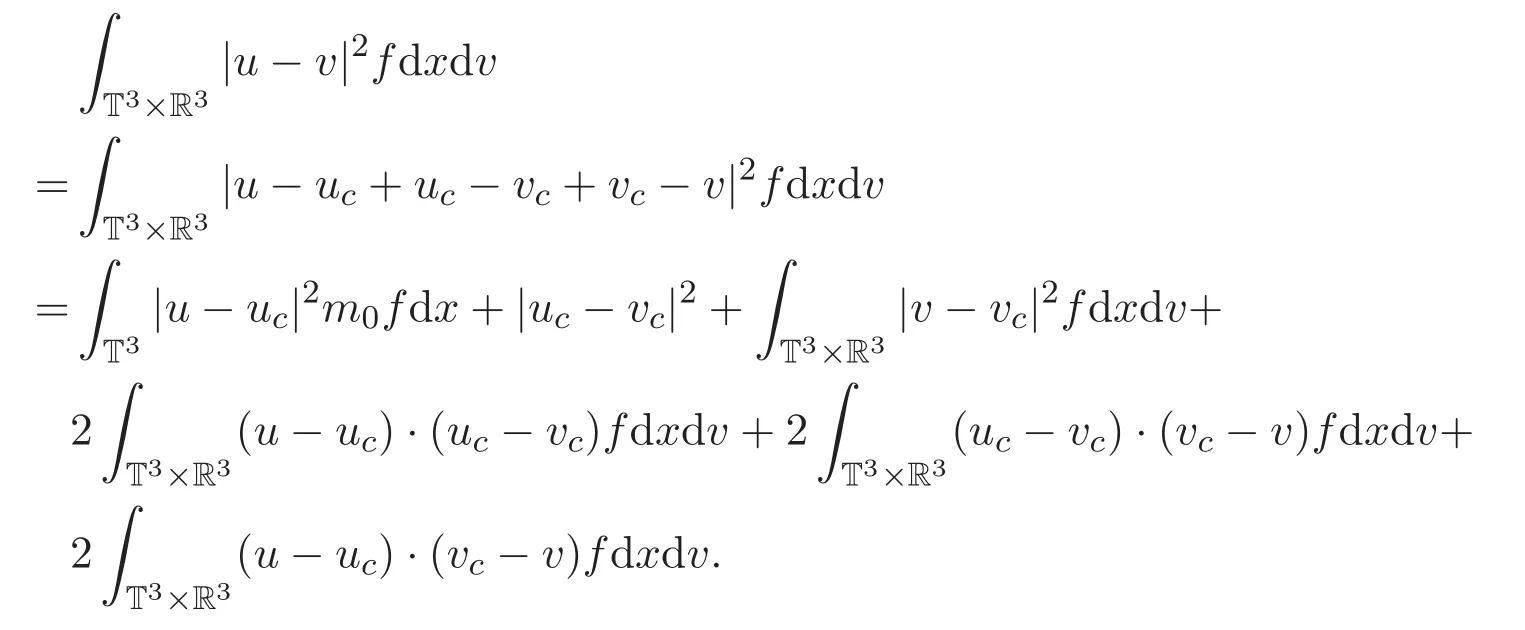
由vc的定義可知

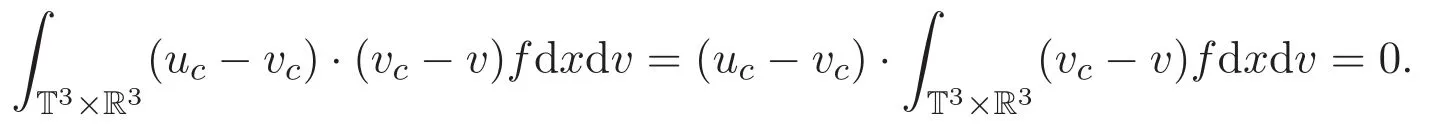
而且

于是

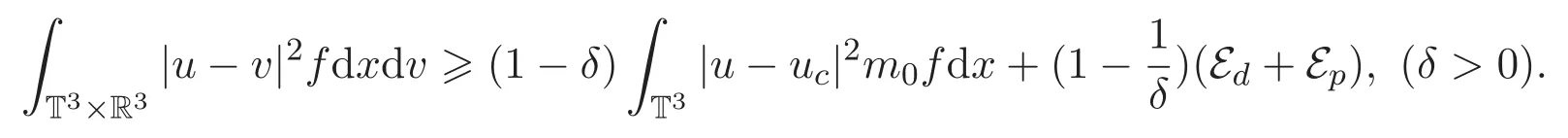
結合(4)式不難得到

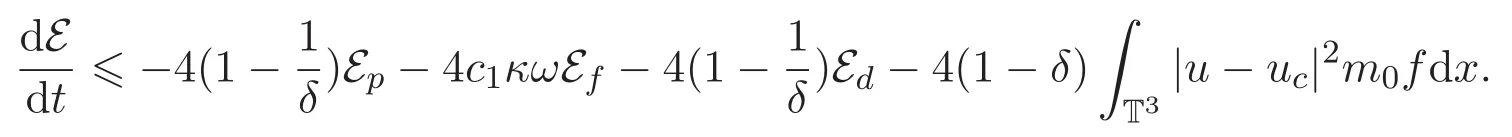
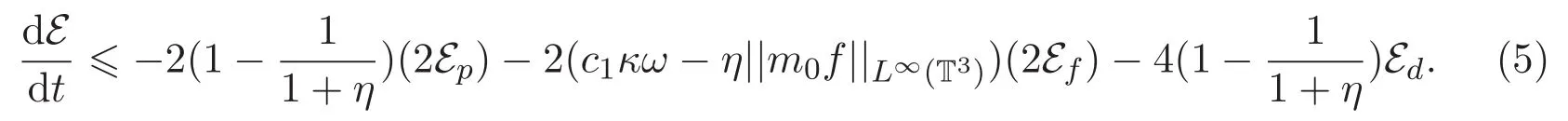
固定

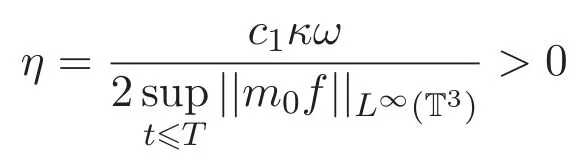
對 (5)式利用 Gronwall′s不等式可得 E(t)6 E(0)e?γt(t∈[0,T)),其中

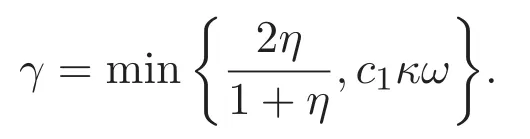
因此,定理1.1得證.