Delannoy數與Schr?der數的一些和式公式
謝叢暉,楊鳳藻
(昆明理工大學理學院,云南 昆明 650500)
1 引言
19世紀末,法國數學家Henri Auguste Delannoy[1]介紹了Delannoy遞歸序列:
d(n,k)=d(n,k?1)+d(n?1,k?1)+d(n?1,k),
其中當n<0或k<0時,n和k為任意整數滿足d(0,0)=1和d(i,j)=0.值得提及的是,d(n,k)有很好的組合解釋,可表示從原點(0,0)到點(n,k)帶有對角步的格路的總數.特別地,當n=k時,Dn=d(n,k)被稱為第 n個 Delannoy數.事實上,Delannoy數可由如下生成函數定義[2]:

或由封閉公式計算如下[3]:

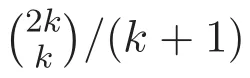
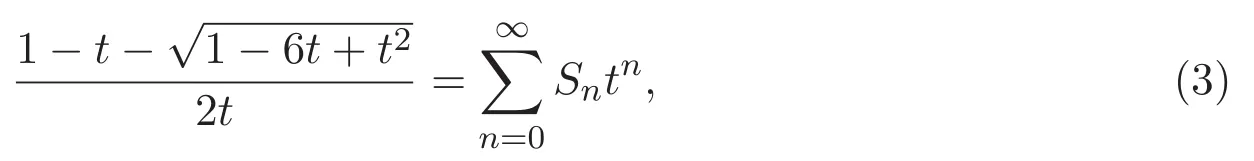
或由封閉公式計算為[3]

Delannoy數和Schr?der數在組合數學中伴有重要的作用,許多學者對它們進行了深入的研究,得到了一些重要的性質[2-8].特別地,文獻[3]研究了Delannoy數和Schr?der數的同余性質,建立了它們與Euler數、Fermat商以及Legendre符號之間的一些深刻的聯系.
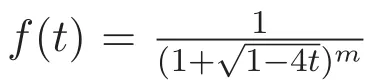
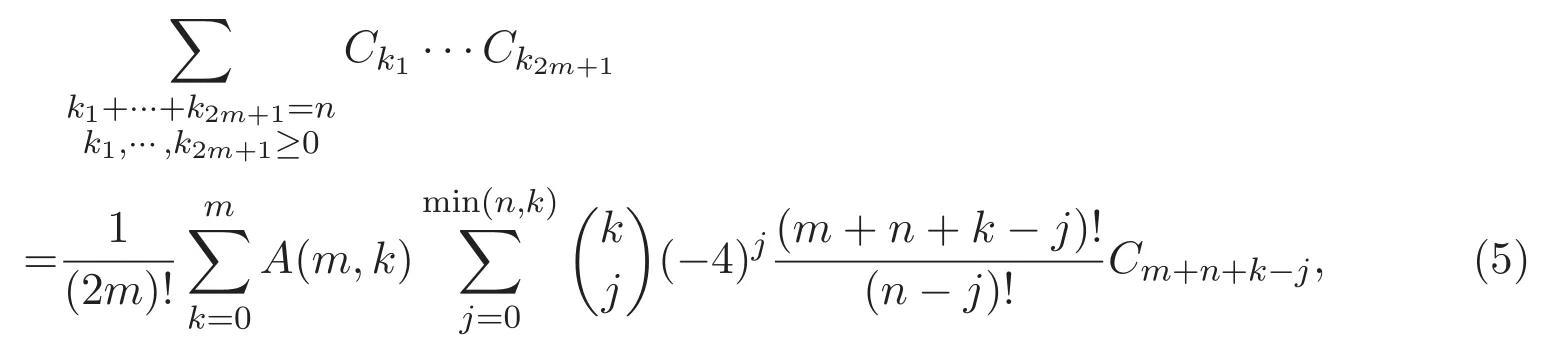
和
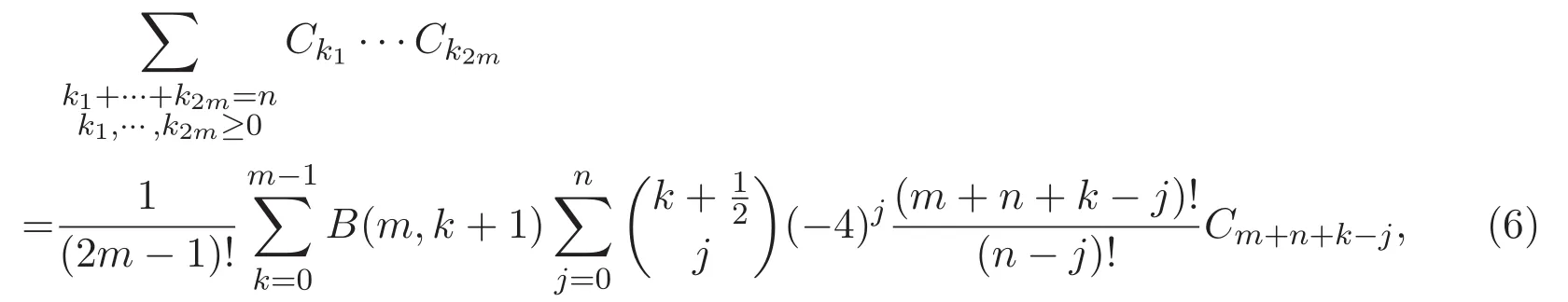
A(m+1,k)=A(m,k?1)?(8k+2)A(m,k)+(4k+2)(4k+4)A(m,k+1);
B(m,k+1)是另一個序列數滿足B(m,0)=0,B(m,m)=1,
B(m+1,k)=B(m,k?1)?(8k?2)B(m,k)+4k(4k+2)B(m,k+1).
進一步地,文獻[10]刻畫出(5)式與(6)式中A(m,k)和B(m,k+1)的準確表示,并得到了一些有趣的同余式.
顯然,(2)式與 (4)式意味著Delannoy數和 Schr?der數與Catalan數之間存在緊密的聯系.鑒于文獻[9-11],本文對Delannoy數和Schr?der數做了進一步的研究,利用分析方法和組合技巧,建立了Delannoy數和Schr?der數的如下和式公式.
定理 1.1 令m是一個正整數.則對于非負整數n,
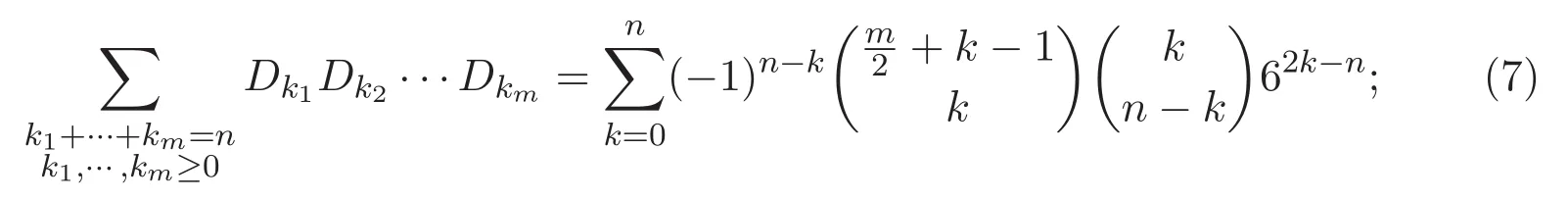
對于正整數n,
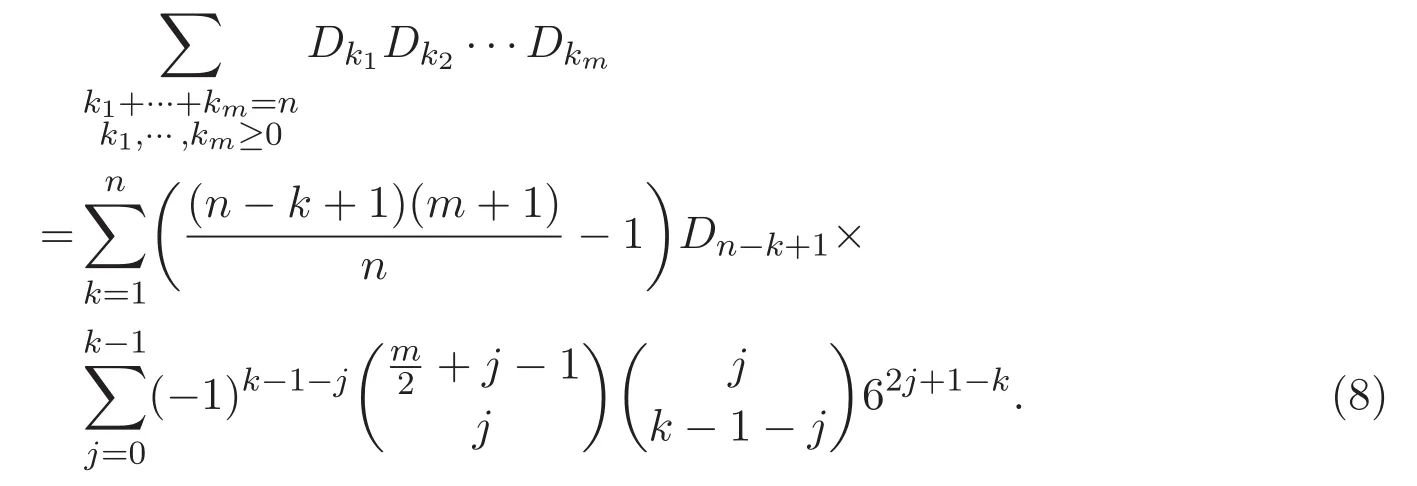
定理 1.2 令m,n是非負整數.則
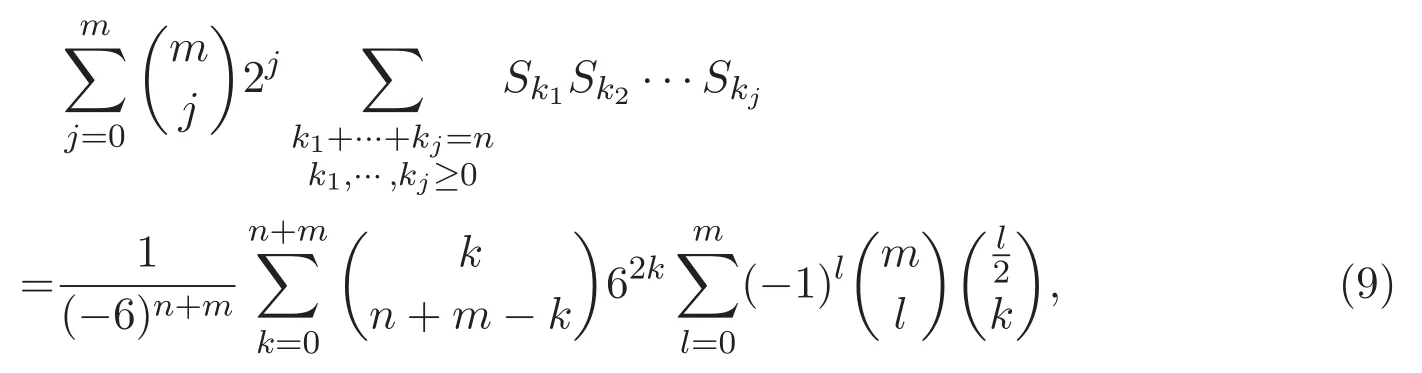
其中當j=0時,等式左邊第二個和式等于1.
注 1.1 在公式(7)中取m=1和m=2分別給出了文獻[2]中(1.3)式與(1.7)式關于 Delannoy數的封閉公式與和式公式.在公式 (9)中取 m=1可得文獻 [4]中 (1.4)式關于 Schr?der數的封閉公式.
2 定理1.1的證明
公式 (7)的第一種證明 由(1)式和Cauchy乘積可知,對于正整數m和非負整數n,
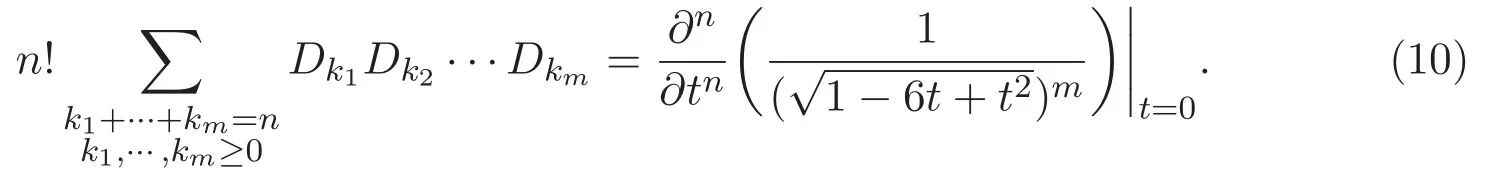
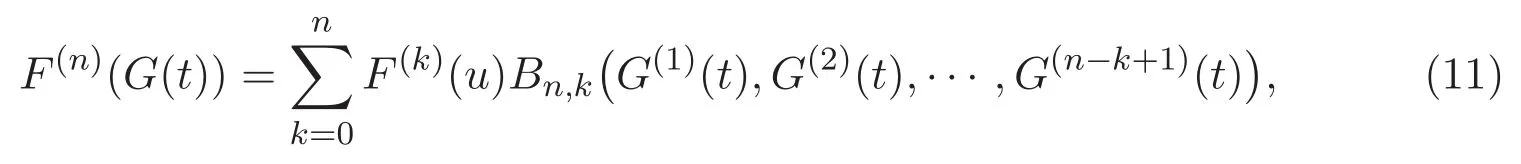
其中 f(n)(x)表示函數 f(x)關于 x的 n階導數,Bn,k(x1,x2,···,xn?k+1)是部分 Bell多項式被定義為[12]
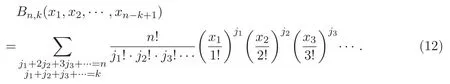
觀察發現,對于非負整數k,
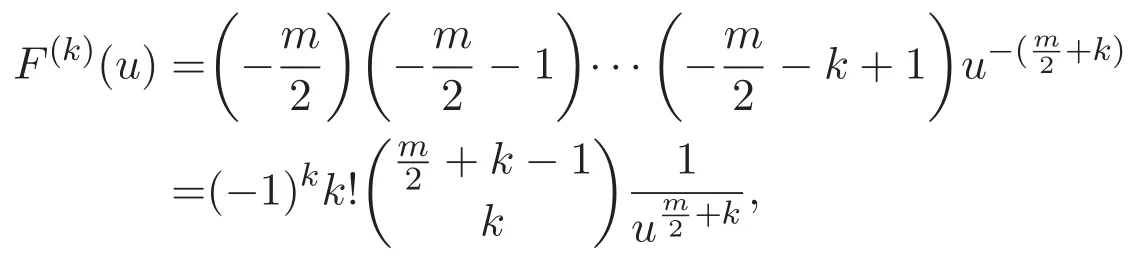
這意味著
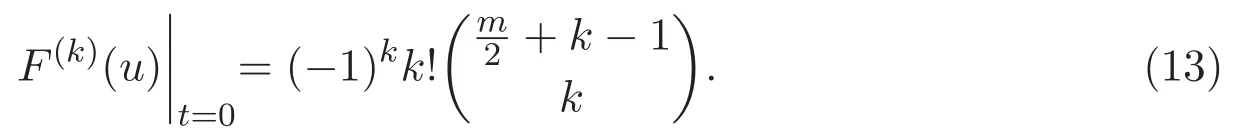
將 (13)式應用到 (11)式中,有
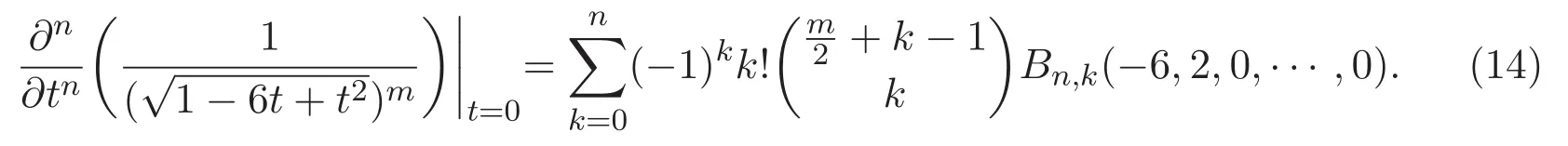
注意到,(12)式表明
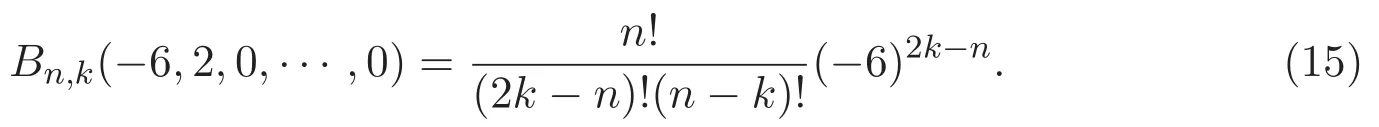
根據(14)式與(15)式,可得
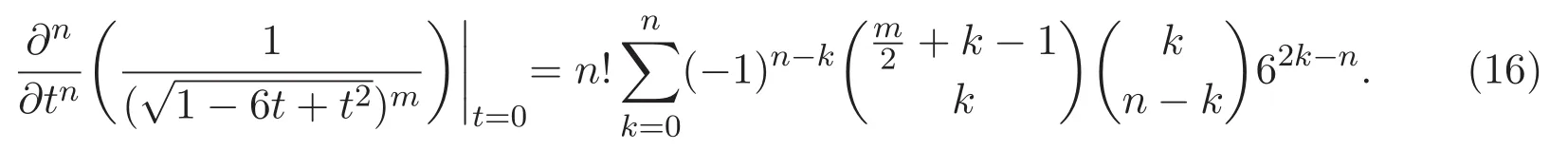
于是,聯立(10)式與(16)式,即得公式(7).
公式 (7)的第二種證明 清楚地,對于任意復數α,
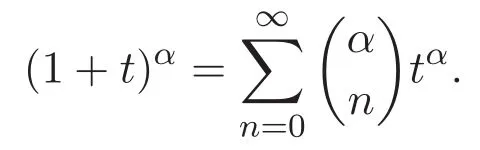
因而,對于正整數m,
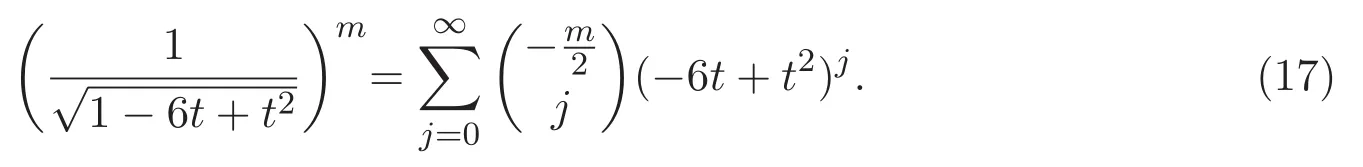
由于
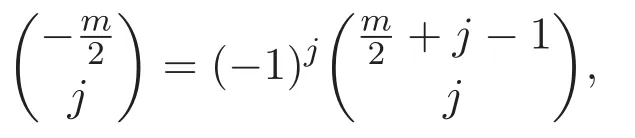
故由二項式定理可知,(17)式可簡化為
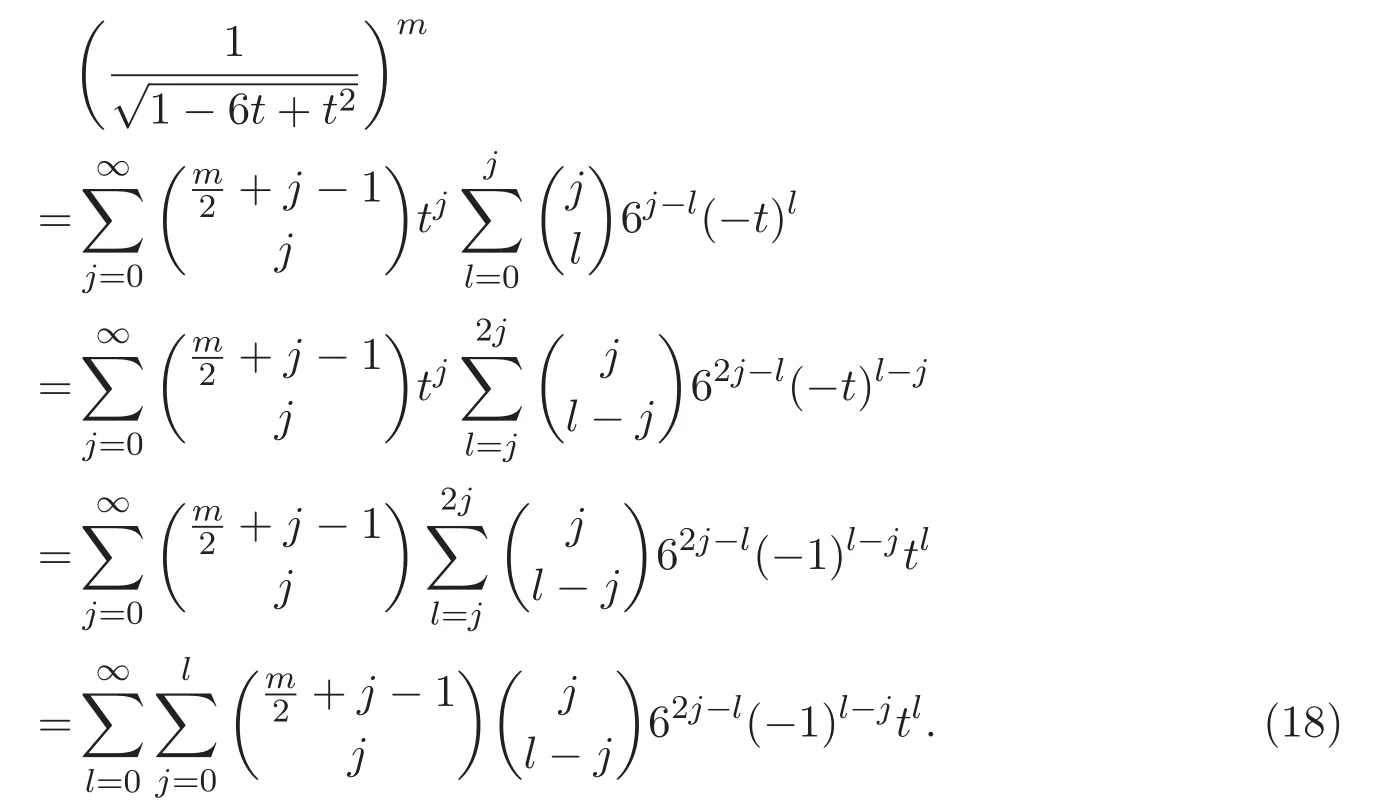
對(18)式關于t作n次求導,可得
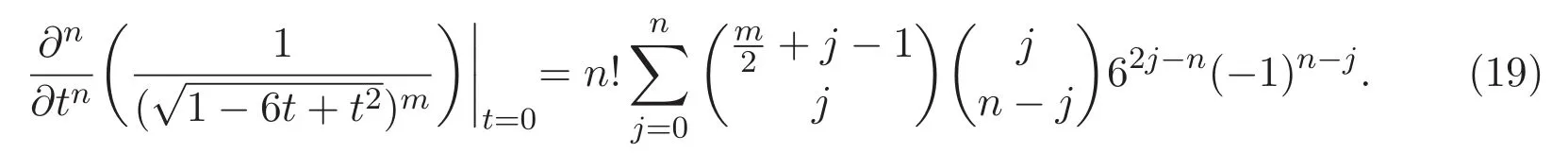
于是,聯立(10)式與(19)式,即得公式(7).
公式 (8)的證明 顯然,對于正整數n,
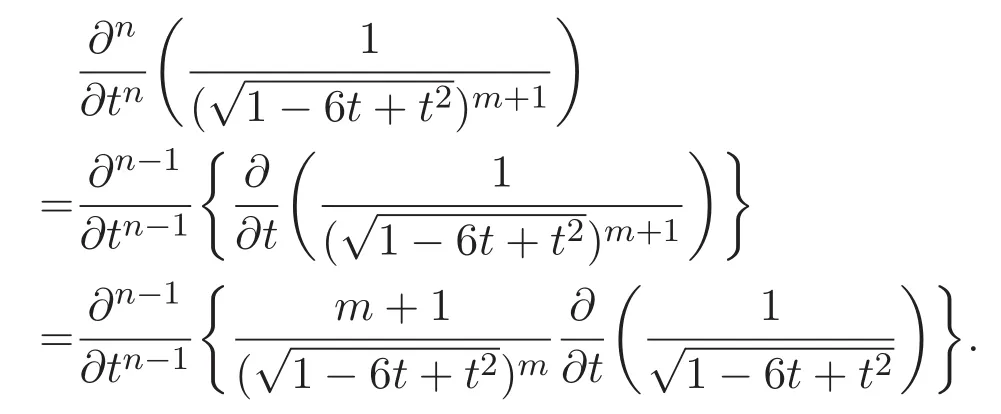
因而,由熟知的Leibniz法則,可得
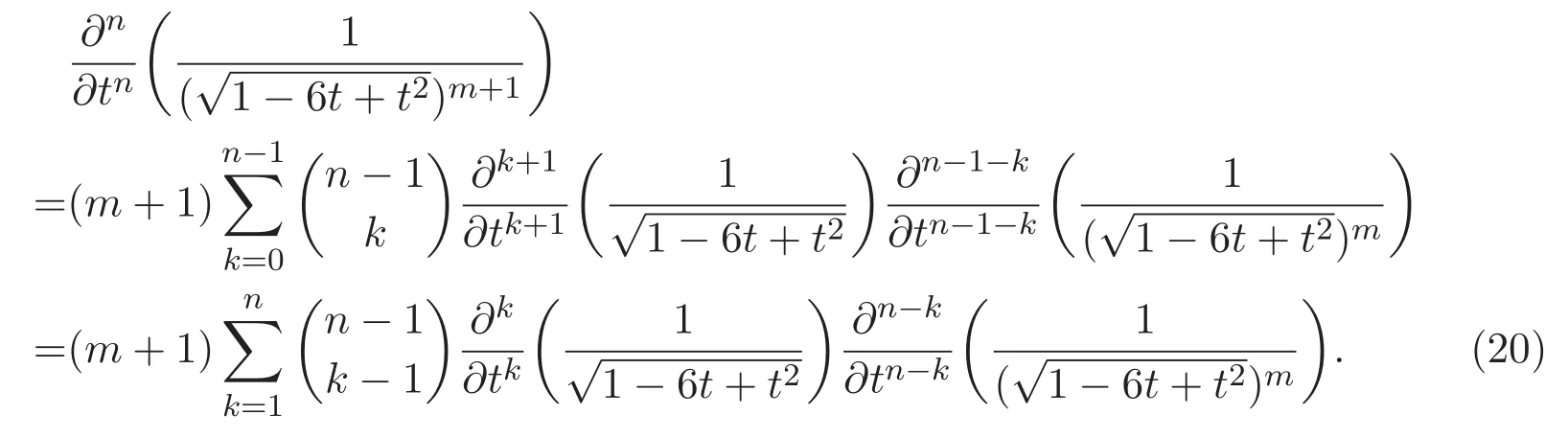
另一方面,根據Leibniz法則,(20)式的左邊能被寫成

聯立(20)式與(21)式,有
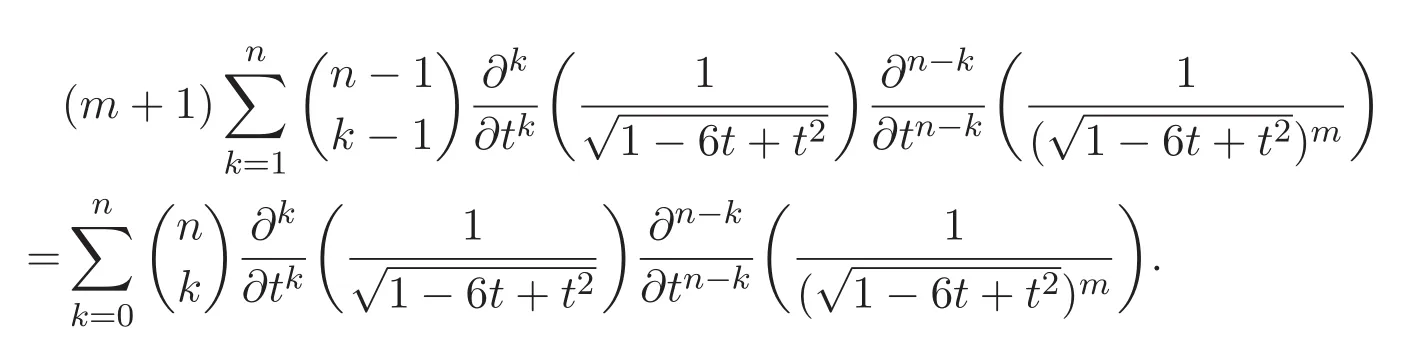
這意味著
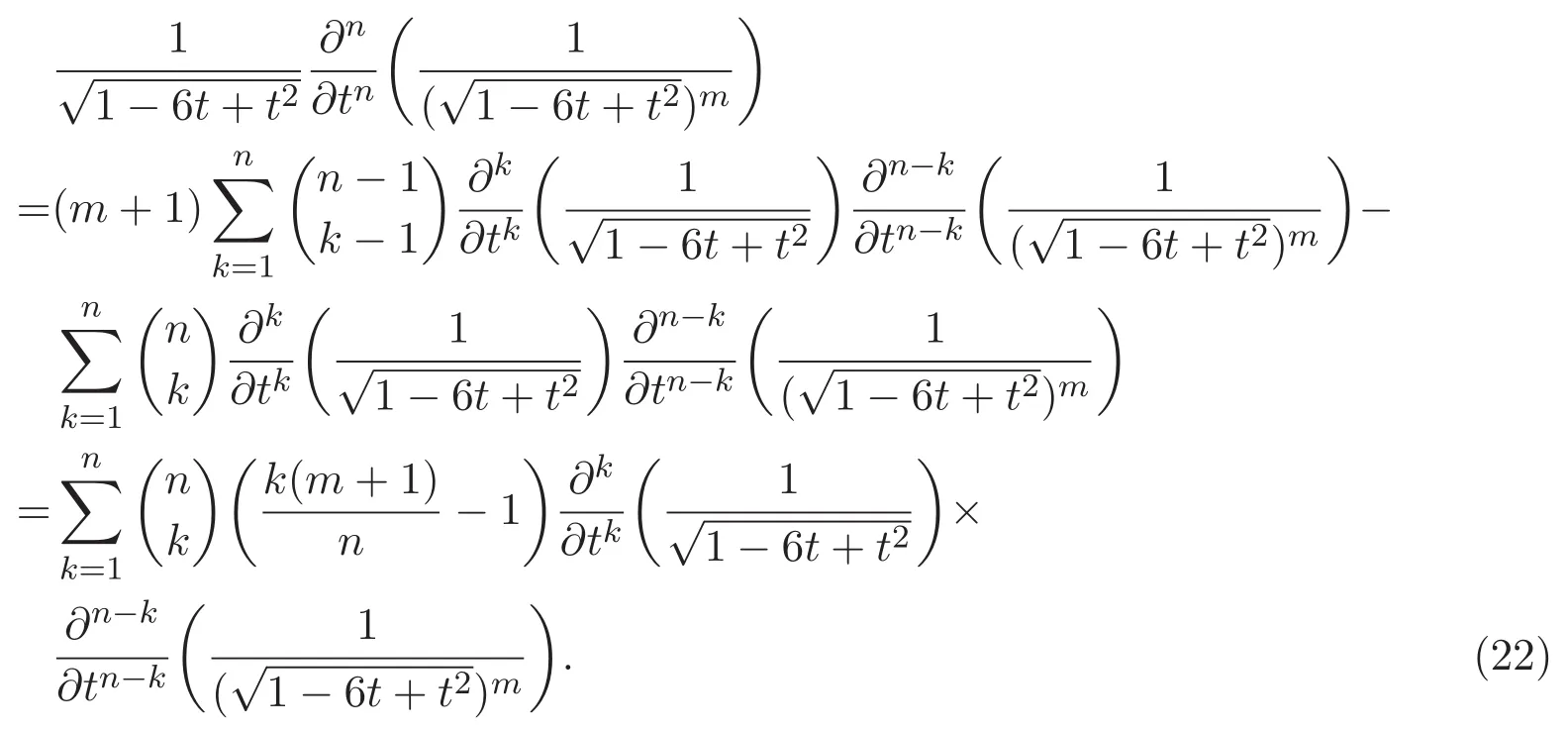
在(22)式左右兩邊分別取t=0,根據(10)式以及公式(7),可得
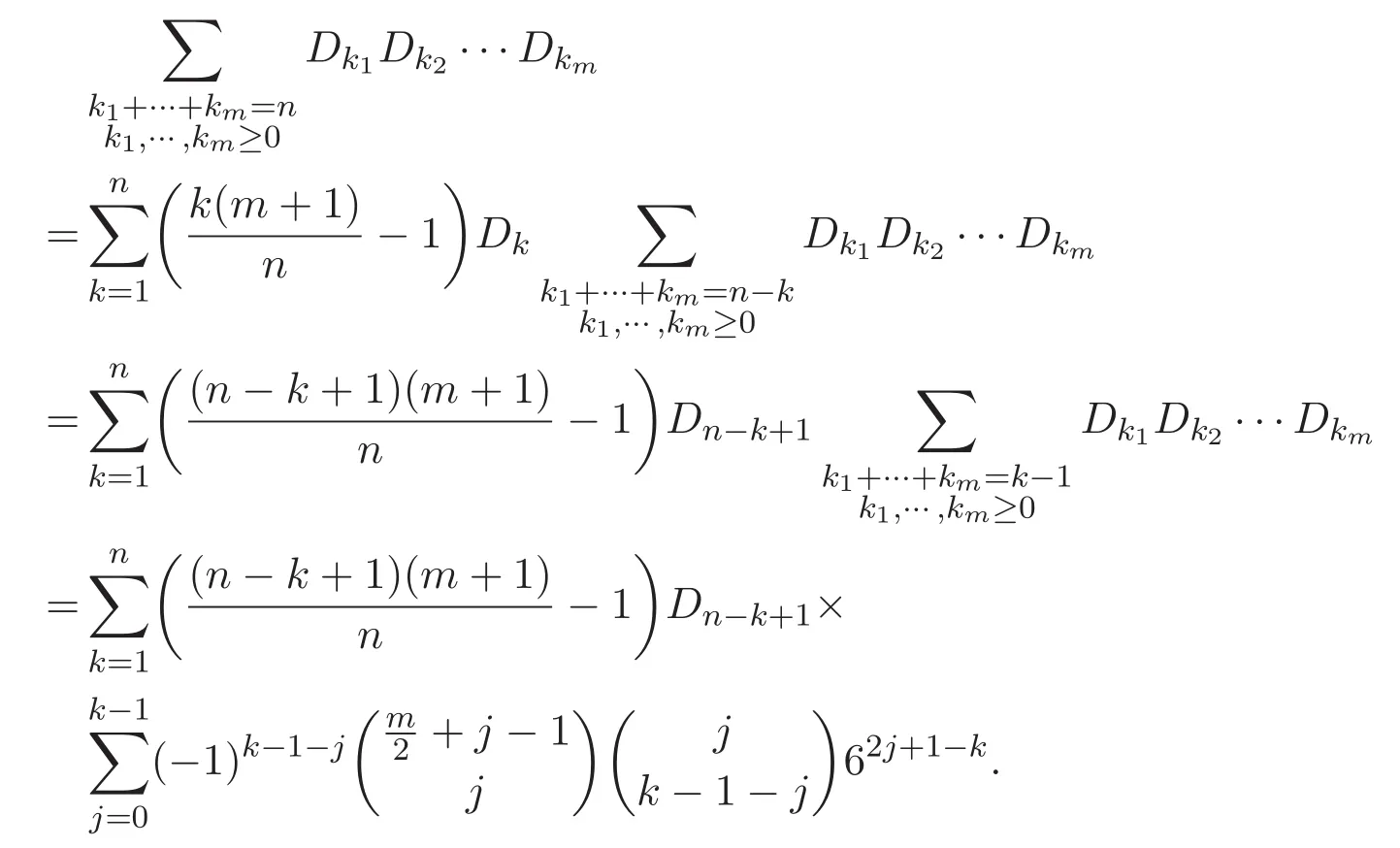
這便完成了公式(8)的證明.
3 定理1.2的證明
由于(3)式能被改寫成
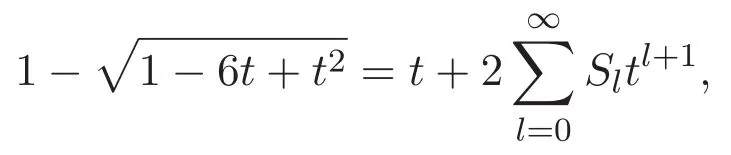
故在以上等式的左右兩邊作m次冪,有
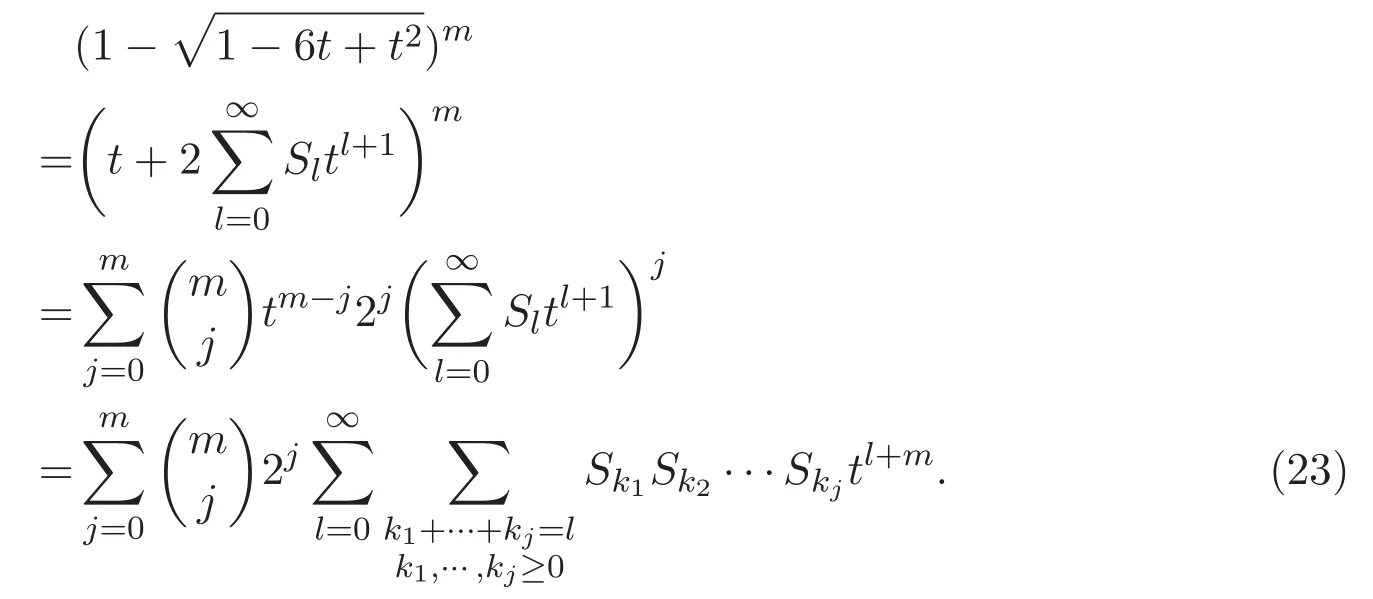
對(23)式關于t作n+m次求導,可得
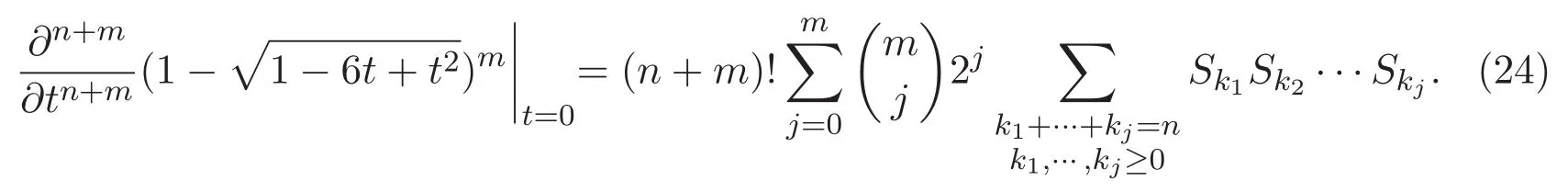
清楚地
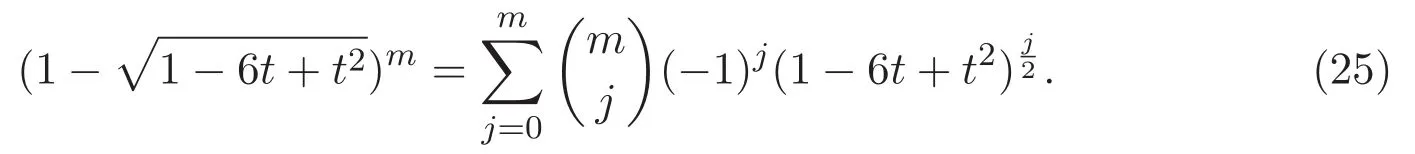
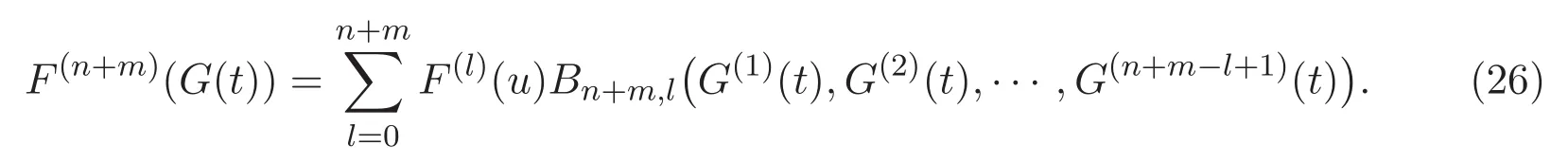
易知

將(27)式應用到(26)式中,根據(25)式以及(15)式,可得
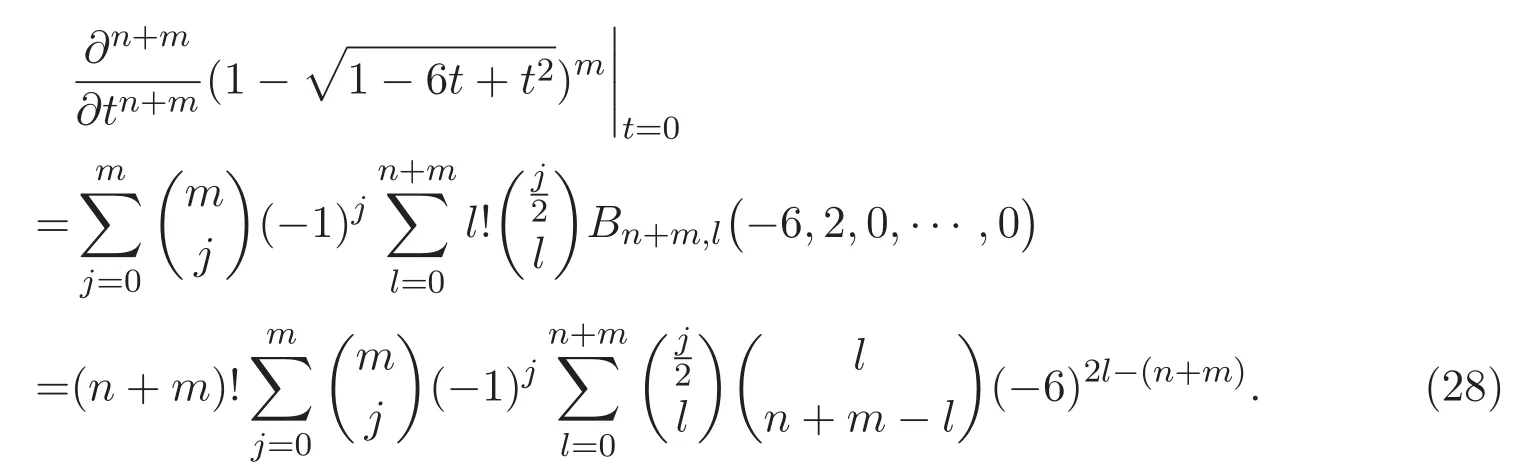
于是,聯立(24)式與(28)式,即完成了定理1.2的證明.
4 結束語
本文利用分析方法和組合技巧,得到了任意多個Delannoy數和任意多個Schr?der數乘積的一些和式公式.文中采用的方法可應用研究另一些著名的多項式序列,如,文獻[13-15]考慮的Fibonacci多項式、Lucas多項式、Dickson多項式.作者將在今后的工作中,對這些多項式序列作進一步研究.
致謝
作者感謝何圓教授給予的指導和幫助.

