一種基于雷達正交極化信息的抗有源假目標干擾方法?
(海軍航空大學青島校區 青島 266041)
1 引言
當前,現代雷達對抗技術發展迅速,有源假目標干擾、距離拖引干擾等技術已成為主流的干擾方式,隨著電子對抗理論技術進一步創新,結合微波電路天線技術、數字射頻存儲技術的應用,使干擾系統能夠轉發被干擾雷達發出的雷達信號,并且在波形、相位、調制上與原信號高度相似。存儲轉發式假目標干擾對雷達探測能力造成嚴重影響,傳統的數據處理以及抗干擾技術只能在時域和頻域上鑒別,不僅大量消耗雷達信號處理資源,而且難以保證鑒別效果。
目前常用的雷達電磁波信息一般集中在時域、頻域、空域當中,極化域是除此之外的另一種電磁波信息來源。極化信息的獲取與處理是現代雷達系統探測處理信息的一個重點部分。通過同時或分時極化體制的雷達對目標探測,獲取極化信息,可以有效對抗無源雜波、有源壓制式噪聲干擾,同時也能夠反制隱身目標,對目標進行識別和檢測查證。本文基于以上背景,以正交極化雷達為研究對象,在分析存儲轉發式假目標干擾和真實目標極化特性的基礎上,通過極化測量技術分別提取其中的極化信息,比較兩者差異,完成目標與干擾的鑒別區分。
2 目標與干擾的極化特性分析
2.1 極化矢量
2.1.1 極化矢量與散射矩陣
雷達的發射波形表示為
式中,A為發射波形的幅值,ht為發射極化的矢量表示,同時也可以理解為目標入射波的極化矢量表示,sm(t)是復合脈沖波形,m是雷達系統對目標探測的次數編號。為方便進行極化域的計算,本文設
雷達系統通過對目標散射波的M次極化測量,其中每次測量能夠得到回波的極化矢量如下:

由式(2)可以看出,回波極化矢量與入射極化矢量存在對應關系,其中,S為散射矩陣。
2.1.2 轉發式假目標的極化矢量
設干擾機發射極化為hjt,接收極化為hjr,干擾信號表示為

式中,B為干擾信號的幅值。
通過極化測量算法,干擾信號極化矢量表示為
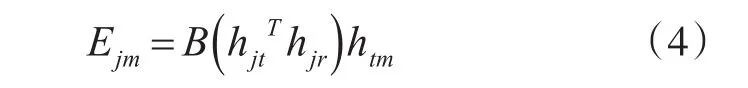
通過干擾極化矢量可得干擾信號的散射矩陣:
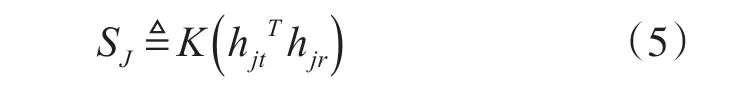
式中,K是干擾機的增益,已知AK=B,則干擾信號極化矢量表示為

2.2 極化散射矩陣
2.2.1 目標回波的極化散射矩陣
采用單極化信號照射目標,回波的極化散射會因目標類型和入射的角度有一些差異,并且大部分目標存在去極化效應。對于中小型目標,可以等效為簡單的線性散射體。使用水平極化波入射,回波中的水平極化部分功率遠高于交叉極化部分,垂直極化同理。若使用圓極化波入射,回波中的圓極化部分功率低于交叉極化部分[8]。雷達探測的目標一般是復雜形體,可等效為由若干簡單形體的組合體,分析表1可知,簡單形體目標的散射矩陣存在高度近似的解,該散射矩陣是非奇異矩陣,因此可知雷達目標回波的散射矩陣一般也是非奇異的。

表1 簡單形體目標散射矩陣
2.2.2 轉發式假目標干擾極化散射矩陣
在2.1節中可知,干擾機對偵查到的雷達信號進行轉發式干擾后形成的反射假目標信號的極化散射矩陣為
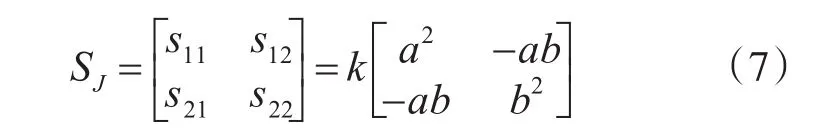
由式(7)可見,單極化轉發式假目標干擾機轉發全極化雷達的假目標信號,其散射矩陣是奇異的、互易的。
2.3 瞬態極化投影矢量(IPPV)
2.3.1 目標回波的IPPV
探測中小型目標時,目標形體可近似為一些簡單的組合體,分析表1可知,當雷達發射線極化信號時,簡單形體散射回波可以表示為

忽略時間關系,由回波信號極化矢量定義IP?PV如下:

式中,“?”表示兩矩陣的克羅內克積。
以規則金屬平面為例,其散射回波IPPV由式(8)、(9)得:

當雷達發射線極化信號時,其散射回波的IP?PV為
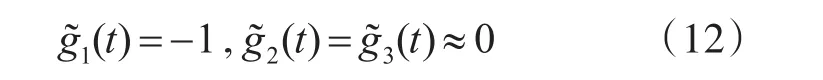
簡單形體目標散射回波的IPPV如表2所示。
由表2可知,簡單形體目標在不同極化方式電磁波激勵下,其散射回波IPPV變化較大,電磁波的入射方向對于IPPV也有一定的影響。

表2 典型簡單形體目標散射回波的IPPV
2.3.2 轉發式假目標的IPPV
已知干擾機天線的極化方式為線極化,由2.1節可知假目標回波信號的表示方式為
將式(13)帶入式(9),得:
按照式(10)的方法進行歸一化,得假目標回波信號的IPPV:

3 目標與干擾的鑒別特征提取
3.1 極化散射矩陣的特征提取
干擾機為單極化天線的轉發式假目標回波的散射矩陣為奇異矩陣,而真實目標回波的矩陣為互易、非奇異的矩陣,此時能夠采用一定量值來描述兩種散射矩陣的區別,對散射矩陣求行列式并歸一化如下:
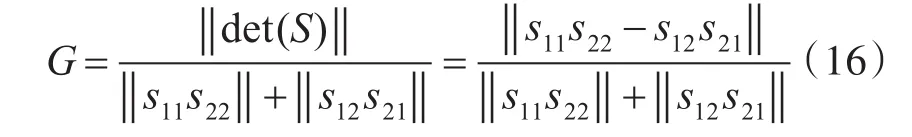
上式中,‖det(S)‖為矩陣S的行列式,“ ‖·‖”表示求模運算,0≤G≤1,為散射矩陣的歸一化行列式值。
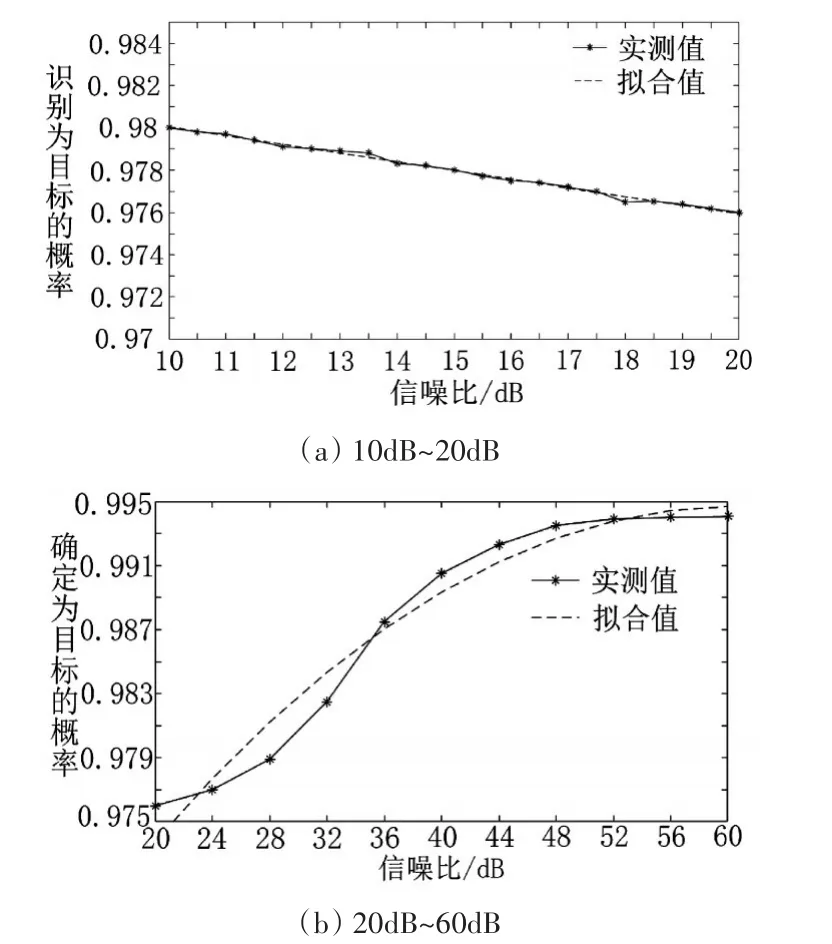
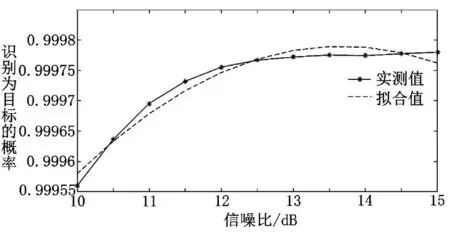
目標回波的G值由目標類型和散射方向決定,此時0 將式(7)的散射矩陣中各個值代入式(16)中,可求得轉發式假目標回波的散射矩陣G=0。而由圖1可知,雷達目標回波的G值有較大概率(0.8左右)在0.8~1的區間內,與轉發式假目標回波的G值差別明顯,因此回波散射矩陣歸一化行列式值可以作為雷達提取的極化信息量之一,用來進行回波性質的判別。 圖1 典型目標的G值分布概率統計圖 使用機載雷達在有假目標干擾的電磁環境下對目標進行探測,在數個周期內可獲得目標回波和干擾回波,將每一周期視為一個分辨單元,此時可以從中提取兩種回波信息。將第i個未知性質的回波IPPV記為 式中:2M為雷達一個數據處理周期包含的脈沖總數。此時雷達工作在正交變極化狀態,設i為奇數時,雷達發射水平極化波形,i為偶數時,雷達發射垂直極化波形。為定量表示一個數據處理周期內回波的IPPV起伏特性,定義參量C為IPPV參考度。 其中:p為矩陣范數的階數,當p=1時,有: 當p=2時,有: 當p=∞時,有: 對于使用線極化天線的干擾機,將式(19)或式(20)分別代入式(2),可求得假目標回波的C值如下: 典型簡單形體散射回波的IPPV參考度如表3。 表3 典型簡單形體目標散射回波的IPPV參考度 由3.1節分析的結果可知,若干擾機是單一極化體制,則其發射的干擾信號散射矩陣的G值趨近于0,目標回波的G值有較大的概率位于0.8~1區間當中,根據G值的差異,可以將其作為鑒別特征量之一。通過數據提取、矩陣分析算法和門限調整設計,歸一化行列式能夠較好地鑒別出目標和干擾,因此設計判別方式如下: 式(23)當中,SC由目標性質以及雷達信噪比決定,在轉發式干擾中,干擾機轉發的雷達回波與被干擾雷達的信號回波在時域和頻域上的差別不明顯,因此在驗證過程中能夠假設信噪比(SNR)等于干噪比(JNR)[6],同時認為散射矩陣中4個元素之間互相獨立,噪聲服從零均值的正態分布,SNR為真實目標回波信號功率與雷達系統總噪聲方差之比,即: JNR定義為干擾信號功率與雷達系統總噪聲方差之比,即: 真實雷達目標回波的散射矩陣與轉發式假目標干擾回波的散射矩陣有一定的特征可以使其加以區分,互易性是其中的一個重要參考量,若信號處理系統中只有一種判別方式,可以將其作為參考,在復雜的判別系統中,互易性判決可以作為鑒別算法的一部分。在本文設計的鑒別算法當中,在信噪比達到要求的前提下,對未知性質的回波信號進行互易性判定,如果鑒別的未知回波矩陣不滿足互易性,則可直接認為是干擾。在實際的雷達系統中,噪聲會破壞散射矩陣的互易性,信噪比是散射矩陣能不能進行互易性判決的先行條件。若回波散射矩陣的交叉極化信噪比過低,只能對散射矩陣進行奇異性判決。 在鑒別前,應當選擇符合當前判決要求的信噪比門限SX、幅度比門限SA和相位差門限SP,門限的大小由鑒別概率決定,必須保持目標的檢測概率在一定要求范圍內。分析可知,低信噪比條件下目標的散射矩陣幅度比分布不夠集中,相位差分布的隨機性大,高信噪比條件下幅度比分布比較集中,相位差接近于0,因此SX可以設為10dB,SA與SP可以根據目標的鑒別概率確定,若鑒別概率要求為95%,取SA=0.1,SP=40°。 由3.2節可知,通過一定的算法,IPPV參考度可以定量衡量目標回波和干擾回波在極化域存在的差別。若IPPV參考度趨近于0,雷達接收到的回波則可能為轉發式假目標干擾。因此能夠采用門限檢測的方法進行IPPV檢測判別:門限值T參考雷達系統的先驗信息計算得出,當CP 為盡量提高信號的鑒別概率,應將回波信號依次進行散射矩陣歸一化行列式的互易性判決和IP?PV校驗,只有當兩次校驗都符合規定門限后才能將接收信號判斷為真實目標回波。采取算法串聯的結構將大幅提高鑒別概率,雖然會提高漏警概率,但是能夠通過增大數據率的方式來進行補償。 根據以上要求設計算法如圖2所示。 圖2 鑒別算法示意圖 圖中,r12=s12+n12,r21=s21+n21,其中n12和n21是交叉極化通道的噪聲,(SNR)max=max(SNR12,SNR21),是交叉極化通道的最大信噪比。 為進一步驗證4.3節當中的鑒別算法,以平板、二面角反射器組合而成的簡單幾何體作為目標,進行仿真試驗,門限值設置如下: 根據4.1中的鑒別方法,圖3給出了模型的鑒別概率,圖3(a)中可以看到,當信噪比逐漸增大,鑒別概率降低,主要原因是此時總信噪比達到了可進行互易性判決的要求,但是互易性判決算法的特性決定了在一定信噪比區間內,檢測概率會出現下降的情況。 圖3 不同信噪比條件下的鑒別概率(奇異性檢驗) 隨著信噪比提高(大于25dB),鑒別概率在一定程度上也會大幅提高。分析鑒別概率變化的總趨勢,與理論基本一致。引入互易性判決而產生的鑒別概率損失可控,并且提高信噪比后,鑒別概率增加的值大于單個算法下的值。 對回波散射矩陣IPPV參考度進行判決時,可根據4.2節中的計算方法,選擇判決門限。根據2.3節中的分析結果,取T=0.8,在信噪比為11dB~13dB的區間內,利用本文的提取和判別方式,計算得出檢驗概率如圖4所示。 圖4 不同信噪比條件下的鑒別概率(IPPV檢驗) 從圖4中可以看出,在既定信噪比區間內,可以較理想的鑒別概率對回波進行鑒別,按照4.3中的算法組合方式對兩種檢測方式進行組合后的綜合計算,得到如圖5所示的結果。由圖5可看出,回波信號順序進行兩種鑒別方式,在信噪比為11dB~13dB時,基本已經達到比較高的水平,在實際應用中,這種鑒別算法一般要在雷達的信號處理階段進行,此時信噪比可以達到15dB以上的水平,此時的鑒別概率可以達到99.98%。 圖5 不同信噪比條件下的鑒別概率(組合鑒別) 本文從目標回波的極化散射矩陣和瞬態極化投射矢量入手,研究了目標回波與干擾信號在這兩種參數上的區別,設計了組合算法,用來鑒別干擾信號,并通過仿真數據驗證了該方法的有效性。通過驗證,按照本文提出的鑒別方法,鑒別效率較高,具有一定的工程使用價值。對于轉發式假目標干擾信號,該算法的鑒別概率也能隨著信噪比和干噪比的提高而提高,所以該算法能夠有效應用在抗轉發式假目標欺騙干擾的環境當中。 經分析表明,單極化干擾機在雷達對抗與反對抗技術不斷革新的情況下,其干擾效果將難以得到保證,隨著相關技術的發展,必將有全極化的干擾機出現。如何有效對抗全極化干擾機,同時在不同的環境中獲取足夠的先驗信息,調整本文算法當中的門限值,以及通過什么方式將該算法應用到雷達抗干擾當中,是下一步研究工作的重點。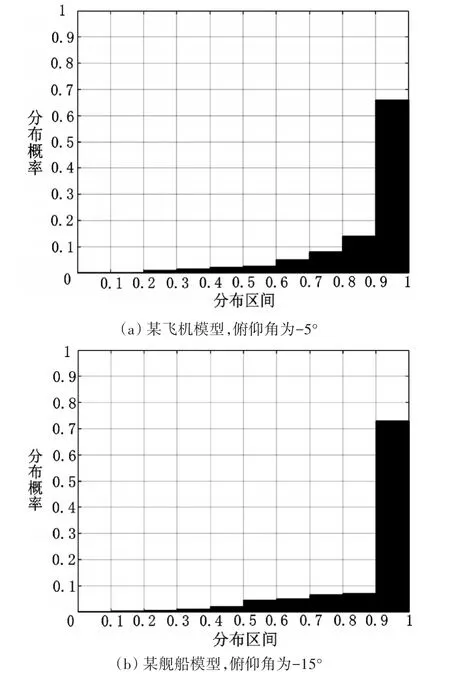
3.2 IPPV特征提取
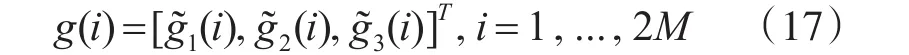

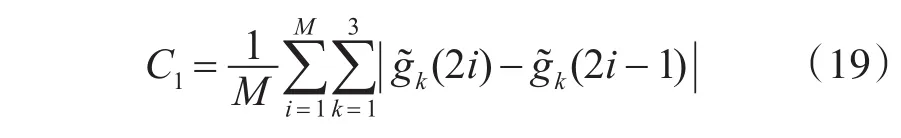
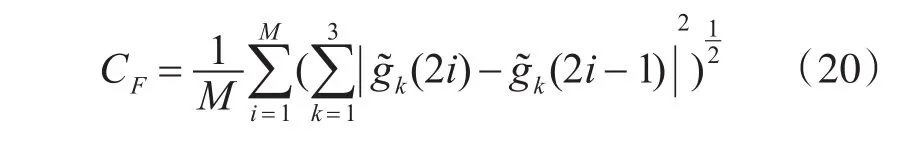

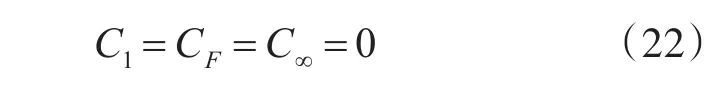

4 門限設定和信息比較
4.1 散射矩陣的歸一化行列式


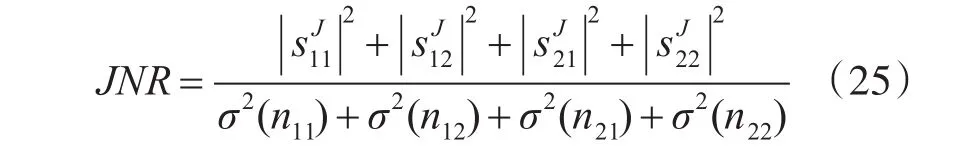
4.2 IPPV的檢驗
4.3 算法的組合方式
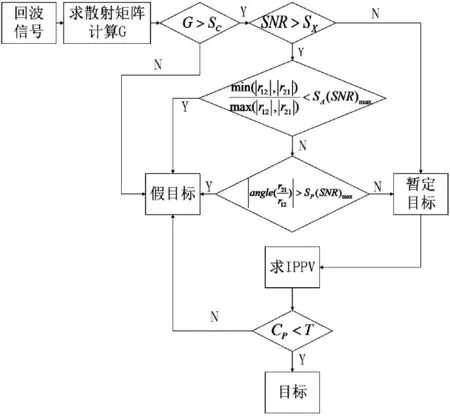
5 鑒別概率分析


6 結語

