空間連桿引緯機構柔性鉸間隙動態特性研究

李 博， 胡 凱， 金國光， 魏 展， 暢博彥

(1. 天津工業大學 天津市現代機電裝備技術重點實驗室， 天津 300387； 2. 天津工業大學 機械工程學院， 天津 300387)

隨著紡織機械行業的迅速發展，無梭織機以其體積小、能耗低、速度快成為目前紡織機械領域的主流產品[1]。劍桿織機作為無梭織機中的典型代表，因紗線適配類型豐富、產品后期可拓展性強等特點，應用越來越廣泛[2]。常見的劍桿織機引緯機構包括共軛凸輪、差動輪系、變導程螺旋、空間連桿、電子引緯等。其中，空間連桿引緯機構因運動規律易控制、傳動效率高等特點，被諸如比利時PICANOL等劍桿織機生產廠商廣泛應用[3]。

在空間連桿引緯機構高速運轉過程中，因制造、裝配、磨損等原因形成的運動副間隙必然會給系統的運行帶來多種影響[4-6]。如：使系統呈現非線性特征，降低機構的運動精度，引起沖擊動載荷造成運動副破壞和磨損等。

針對機構間隙的研究，始于20世紀70年代，Earles等學者提出了含間隙機構的連續接觸模型，該模型將間隙等效為長度固定且無質量的間隙桿，通過間隙桿的速度突變，來判斷是否發生碰撞[7]。在此基礎之上，研究人員將間隙碰撞過程描述為“接觸—碰撞—分離”的3種狀態轉化，建立了間隙運動副經典碰撞模型[8]。然而，以上模型均無法準確求解間隙碰撞力、間隙偏心距軌跡等動態特性。

要研究含間隙系統的完整動態性能，就必須考慮柔性鉸間隙作用機制，建立包含彈簧力和阻尼力的非線性接觸碰撞力模型[9]。早期的線性簡化模型在其描述碰撞過程中沒有體現柔性鉸壓縮和恢復過程中的能量耗散[10]。隨后出現的Kelvin-Voigt線性彈性模型包含了接觸剛度和阻尼，但是沒有表征恢復系數和初始碰撞速度[11]。Hunt等人在Kelvin-Voigt模型的基礎之上提出了Hunt-Crossley模型，奠定了現代非線性接觸碰撞力模型的基本框架[12]。近年來，Lankarani、Flores、Bai等在Hunt-Crossley模型的基礎上，提出了多種考慮能量耗散因素的非線性間隙碰撞力模型[13-15]。目前，國內將柔性鉸間隙碰撞模型應用到空間連桿引緯機構運動學與動力學分析中的研究相對較少，相關工作的開展尤為迫切。

本文針對空間連桿引緯機構進行運動學分析，將柔性鉸間隙作用機制引入到系統的動態求解中，結合Lankarani-Nikravesh模型和Newton-Euler方法建立動力學模型，研究間隙對引緯過程的直接影響，為今后劍桿織機的穩定性研究、性能優化和磨損評估等工作奠定了理論基礎。

1 空間連桿引緯機構簡介

劍桿織機因其換色便捷，適宜多色緯織物，而被廣泛應用于色織布、雙層絨類織物、毛圈織物和裝飾織物的生產[16]，其引緯機構結構示意圖如圖1所示。

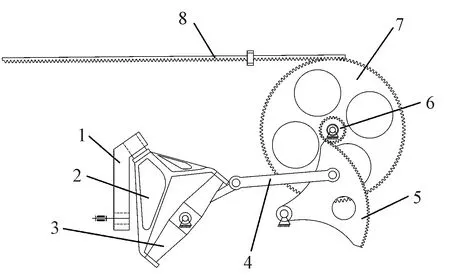
1—傳動曲柄；2—空間連桿；3—十字搖軸；4—連桿；5—扇形齒輪；6—傳動小齒輪；7—劍帶輪；8—劍帶。

劍桿織機的空間連桿引緯機構由3個部分組成，分別是空間連桿組成的運動輸入部分(圖1中的1、2、3)、平面連桿組成的運動傳遞部分(圖1中的4)和由齒輪輪系、劍帶、劍頭組成的動程放大部分(圖1中的5、6、7、8)。通過動程放大部分，可將空間連桿的運動規律放大輸出到劍帶和劍頭處。

整個機構的構件通過大量鉸接副連接，具有良好的緊湊性和運動穩定性，同時具有主軸轉速高、傳動路線短等優點，但該機構在運動規律設計方面較為復雜，裝配精度要求較高，長時間運行，容易產生相對較大的運動副間隙;因此，有必要深入研究間隙對空間連桿引緯機構的動態性能影響。

2 柔性鉸間隙接觸碰撞力模型選擇

本文采用柔性鉸間隙模型描述機構鉸間間隙碰撞(見圖2)。考慮到間隙碰撞過程中運動副中心的碰撞變形，將整個碰撞運動過程描述為分離、碰撞、接觸、壓縮(恢復)等幾種狀態，通過間隙偏心距與間隙值的差值，判斷碰撞是否發生。其中：RJ為軸銷半徑,mm;RB為軸套內徑的半徑,mm;c為間隙尺寸,mm。

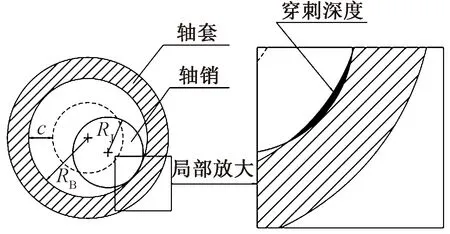
圖2 含間隙轉動鉸模型(柔性鉸)

間隙碰撞同時存在法向碰撞力和切向碰撞力，而高速劍桿織機的空間連桿引緯機構通常具有良好潤滑的工況條件;因此，暫不考慮含間隙運動副中切向碰撞力即摩擦力對機構運動帶來的影響。在碰撞力模型的選取中，常用的模型包括簡易接觸碰撞力模型、Lankarani-Nikravesh模型、Flores模型、Hunt-Crossley模型等。通過文獻[18]可知：簡易模型不考慮能量耗散，不能表征間隙碰撞過程中的阻尼力；Hunt-Crossley模型適用于高恢復系數的正碰撞；Flores模型適用于完全彈性或者完全塑性的碰撞環境；Lankarani-Nikravesh模型能夠反映碰撞體的材料性質、幾何特征及運動狀態對碰撞過程的影響，其碰撞壓縮與恢復階段的能量耗散基本上相當。綜上，本文選用Lankarani-Nikravesh模型描述工況下空間連桿引緯機構的間隙碰撞。

3 空間連桿引緯機構的動態建模

3.1 無間隙狀態下機構的運動學分析

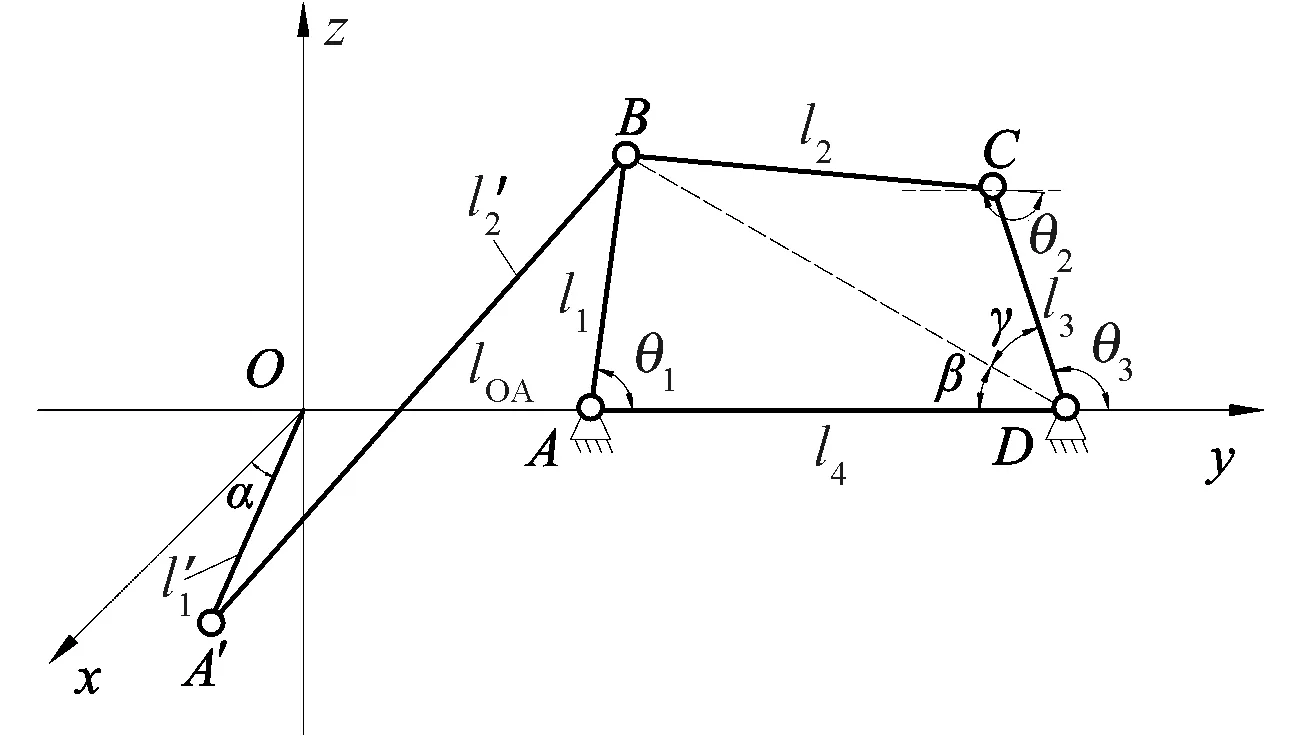
圖3 空間連桿機構簡化模型

首先對空間連桿部分應用矢量法建立運動學模型

(1)

將上述向量分別向x，y，z軸投影，可得到

(2)

求解可得桿BC的運動規律

(3)

通過矢量法對桿AD的運動規律求解得

(4)

(5)

由式(4)、(5)可求得θ3如下式

θ3=π-β-λ

(6)

桿CD是由扇形齒輪簡化而得到的，扇形齒輪通過與小齒輪的嚙合，帶動劍帶輪和劍帶的往復運動，進而完成引緯動作,因此，劍頭的運動規律可通過以下表達式求解：

(7)

式中：d1、d2、d3分別為扇形齒輪、小齒輪和劍帶輪的分度圓直徑，mm。

將式(7)對時間t求導，即可得到理想無間隙狀態下劍頭速度和劍頭加速度的表達式。

本文研究對象為應用于JWG1732型高速劍桿織機中的空間連桿引緯機構，下文動力學分析和工程實例均以此機構為研究對象，不再重述。參與計算的主軸轉速選擇500 r/min，經過測量，d1、d2、d3分別為：250、65和369 mm，其余各構件長度見表1。

表1 各構件長度

將各參數代入式(7)并通過編程仿真，即可求解理想無間隙狀態下劍頭的運動學規律。運動規律如圖4所示。

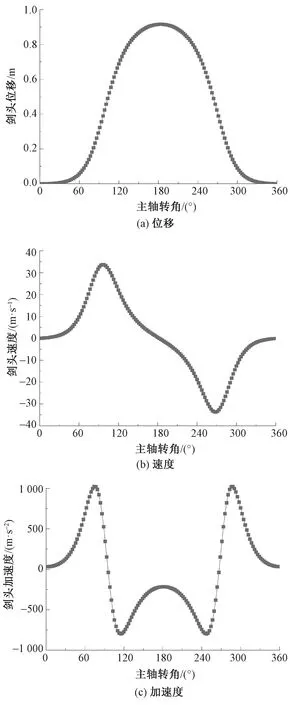
圖4 理想無間隙狀態下劍頭運動規律

由圖4可知：當主軸轉角為60°～105°時，劍帶帶動劍頭進行送紗運動，此時為了增加工作效率，需要劍頭速度迅速增加；當主軸轉角為105°～255°時，引緯劍頭和接緯劍頭進行緯紗交接，劍頭加速度變化較為平緩；當主軸轉角為255°～300°時，劍頭回程，劍頭速度呈現快速退回的運動特性;當主軸轉角為300°～360°與0°～60°時，紗線準備再次進入梭口，此時劍頭速度和加速度曲線相對平穩，以確保劍頭準確夾持緯紗。

3.2 用于柔性鉸間隙作用的動力學建模

在多體系統動力學的建模方法中，常用的方法分別是Newton-Euler方法、Lagrange方法和Kane方法。Newton-Euler方法可應用在系統構件數量有限，結構不復雜的機構中，其特點是表達式物理意義明確，拓展性強；Lagrange方法通過對系統整體動能、勢能的求解，在系統構件相對較多的時候比Newton-Euler方法具有更少的方程求解量；Kane方法兼具矢量法和分析法的特點，但其求解偏速度、偏角速度等表達式物理意義不明晰，且廣義速率的選取較難。綜上，本文采用Newton-Euler方法對含間隙系統建立動力學模型。

圖5示出含間隙連桿部分。B為含間隙運動副，s1、s2和s3分別為連桿AB、BC和CD的質心；e為間隙運動副B處的偏心距矢量；φ為偏心距矢量與y軸的夾角；F1y、F1z分別為接觸碰撞力FN在y軸和z軸方向的分量。

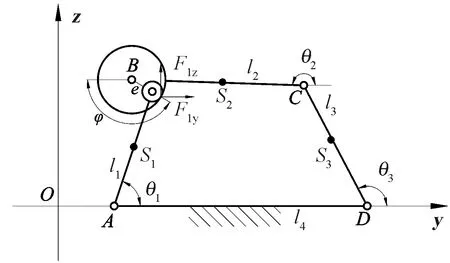
圖5 含間隙連桿部分

通過前文的對比分析，接觸碰撞力模型選取Lankarani-Nikravesh模型，即

(8)

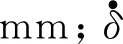
δ=e-r

(9)

式中，r為運動副間隙，mm。

間隙偏心距e與y軸的夾角為φ可表示為

(10)

通過Newton-Euler方法對系統建立動力學模型，拆分桿BC并受力分析可得

(11)

式中：R1為B運動副處的軸銷半徑,mm；J2為桿BC的轉動慣量,kg·m2；m2為桿BC的質量,kg；F2y和F2z為C副處的約束反力在y軸方向和z軸方向的分量。桿AB和桿CD也需要通過同樣的方法進行分析。

通過矢量法對B、C、D副進行描述，并整理上式可得到如下動力學方程：

(12)

(13)

式中：J3為桿CD的轉動慣量，kg·m2；m3為桿CD的質量，kg。

4 工程實例分析

4.1 具體工程實例分析

在實際工業生產中，通常情況下引緯機構運動副的靜態間隙為0.05 mm左右，而在高速運轉過程中，運動副間隙可達到0.20 mm及以上。考慮到系統運行過程中的沖擊動載荷變化及長時間運行產生磨損，以下分析的間隙取值分別為0.05、0.2和0.5 mm。另，除表1涉及的構件長度參數外，其他相關參數取值見表2所示。

表2 相關參數取值

通過模型計算可得到以下動態特性曲線，見圖6所示。

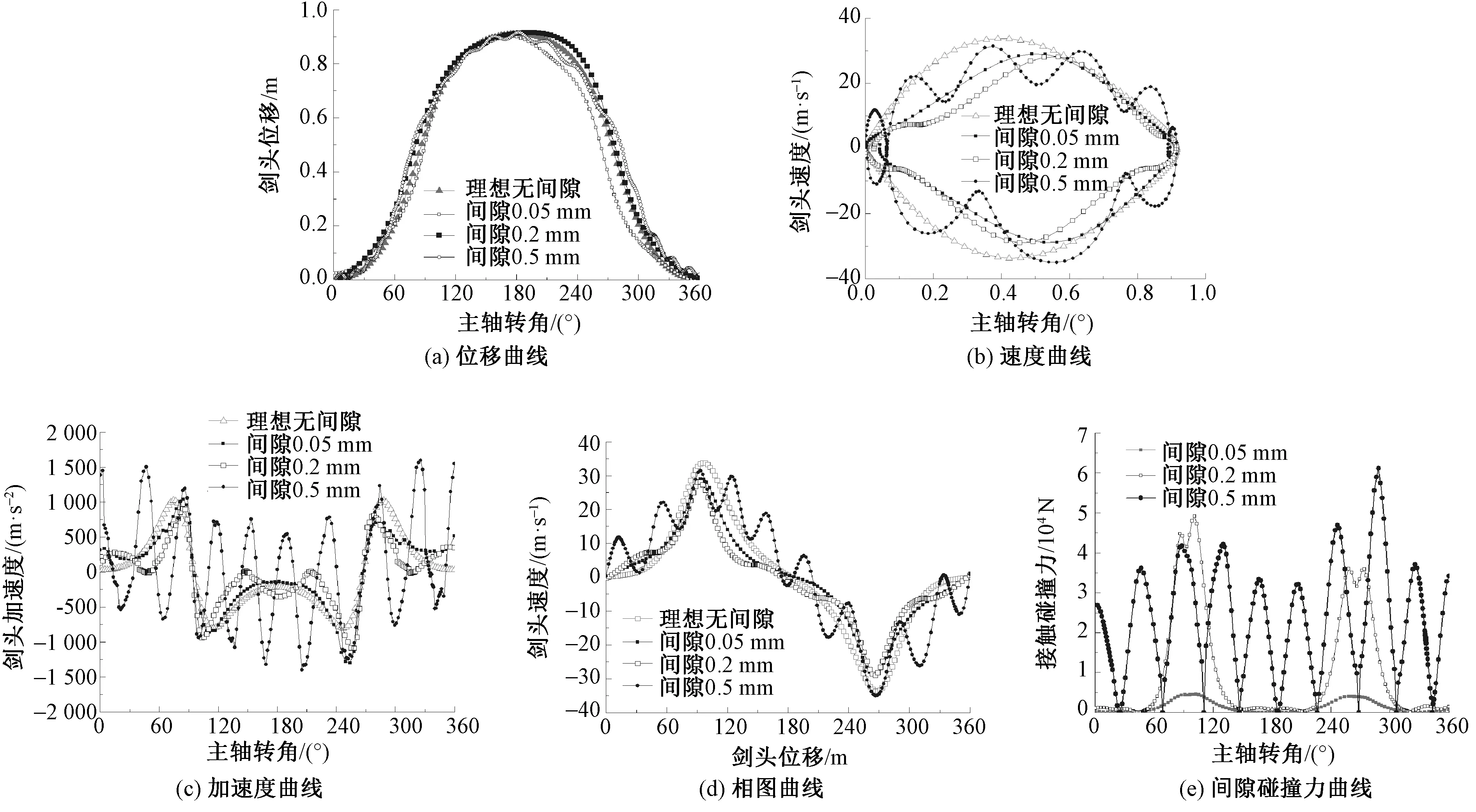
圖6 不同間隙下系統的動態特性

由圖6可知：間隙在0.05～0.5 mm范圍內變化時，對于劍頭位移的峰值影響是相對較小的；當間隙大于0.2 mm以后，劍頭速度在整個運動周期內呈現較大幅度波動，參照系統相圖可知，在主軸轉角0°～60°與300°～360°這2個區間內，劍頭速度波動頻率相對較高，運動規律中“快進”和“急回”特性的穩定性受到削弱，這將對織機重新拾取紗線并再次進入梭口帶來不利影響；間隙對于劍頭加速度的作用是最大的。當間隙為0.05 mm時，加速度曲線波動較小。當間隙達到0.2 mm時，加速度曲線在主軸轉角105°～255°區間內出現了1個較大幅度的波動，此時引緯劍頭與接緯劍頭正在進行緯紗交接，劍頭加速度的波動會對平穩接緯帶來一定程度的干擾。而當間隙繼續增加至0.5 mm時，加速度曲線在整個運動周期內劇烈波動，這將會造成劍頭對紗線的沖擊力大幅度增加，斷緯率也隨之提升；最后，通過不同間隙下碰撞力的對比可知，當間隙在0.05～0.2 mm之間時，碰撞力存在2個較突出峰值，分別出現在主軸轉角60°至120°和240°～300°這2個區間，結合引緯工藝可知，在劍頭的送紗運動和回程過程中，含間隙運動副會出現相對較多的磨損。當間隙逐漸增大至0.5 mm時，隨著碰撞的多次出現，間隙碰撞力在整個運動區間內大范圍振蕩，運動副磨損區域大幅增加。綜上，為了保證引緯效率、織物質量和機構運行壽命，應盡可能將運動副間隙控制在0.5 mm以內。

4.2 虛擬樣機檢測校核及剛性鉸方法對比

為校核本文動力學建模方法的準確性并討論該方法的適用范圍，建立以實測數據為基礎的虛擬樣機(見圖7)。對虛擬樣機檢測數據進行采集，并與目前工程領域中常見的剛性鉸建模方法進行對比。

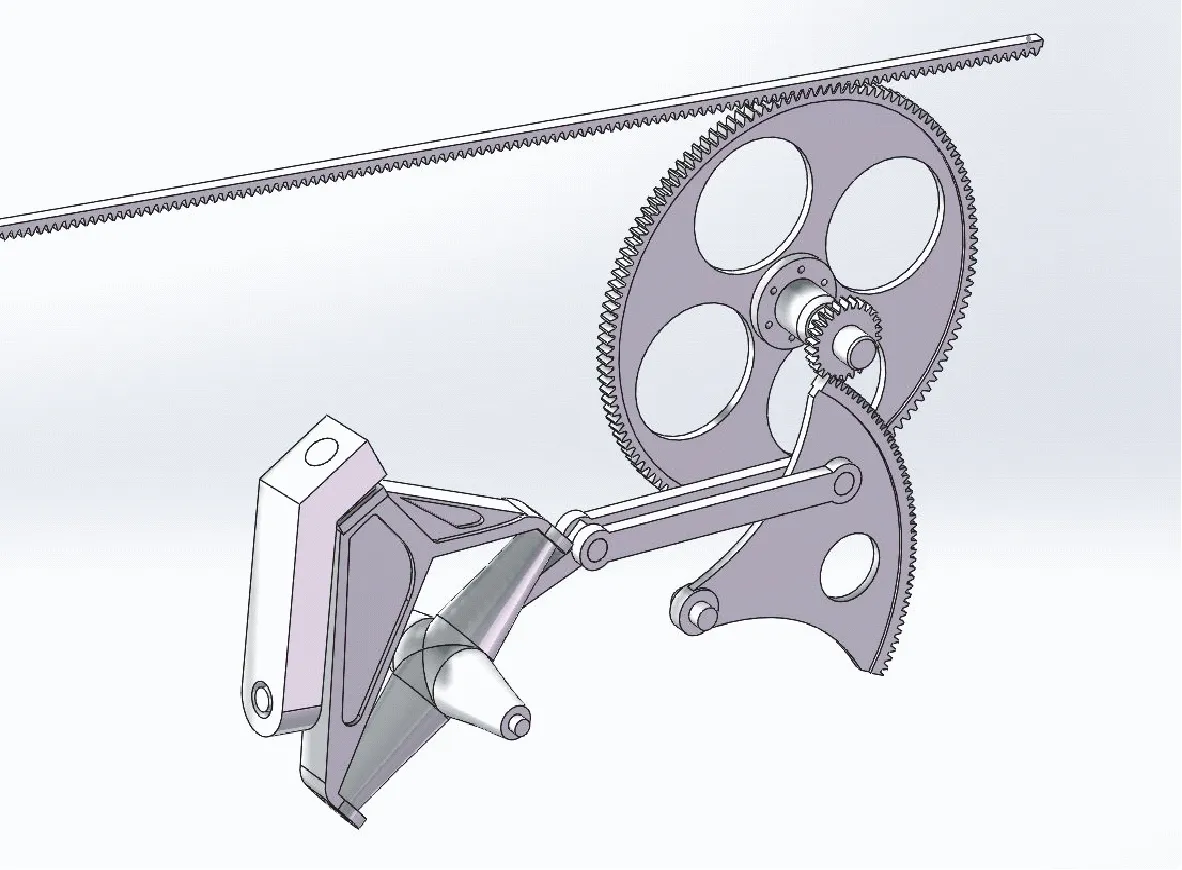
圖7 空間連桿引緯機構虛擬樣機

首先對速度曲線進行對比，如圖8所示。在間隙為0.05 mm時，柔性鉸方法、剛性鉸方法和虛擬樣機檢測數據無論從幅值還是數值曲線的重合度都是比較高的；當間隙提高到0.2 mm時，柔性鉸方法和虛擬樣機檢測數據的速度曲線在主軸轉角120°～240°區間內出現了一定范圍的波動，而剛性鉸方法則呈現變化不大的小范圍波動，這會導致其對于接緯過程穩定性的判斷出現較大偏差；而當間隙進一步增大到0.5 mm，柔性鉸方法和虛擬樣機檢測數據仍具有較高重合度，而剛性鉸方法通過局部放大后可看到其速度曲線出現了高頻率、不連續的振蕩。造成上述現象的原因是剛性鉸方法假定碰撞瞬間完成且軸銷與軸套立即分離，沒有考慮連接鉸的柔性變形，因此存在速度不連續且波動幅值沒有進一步提升的現象。

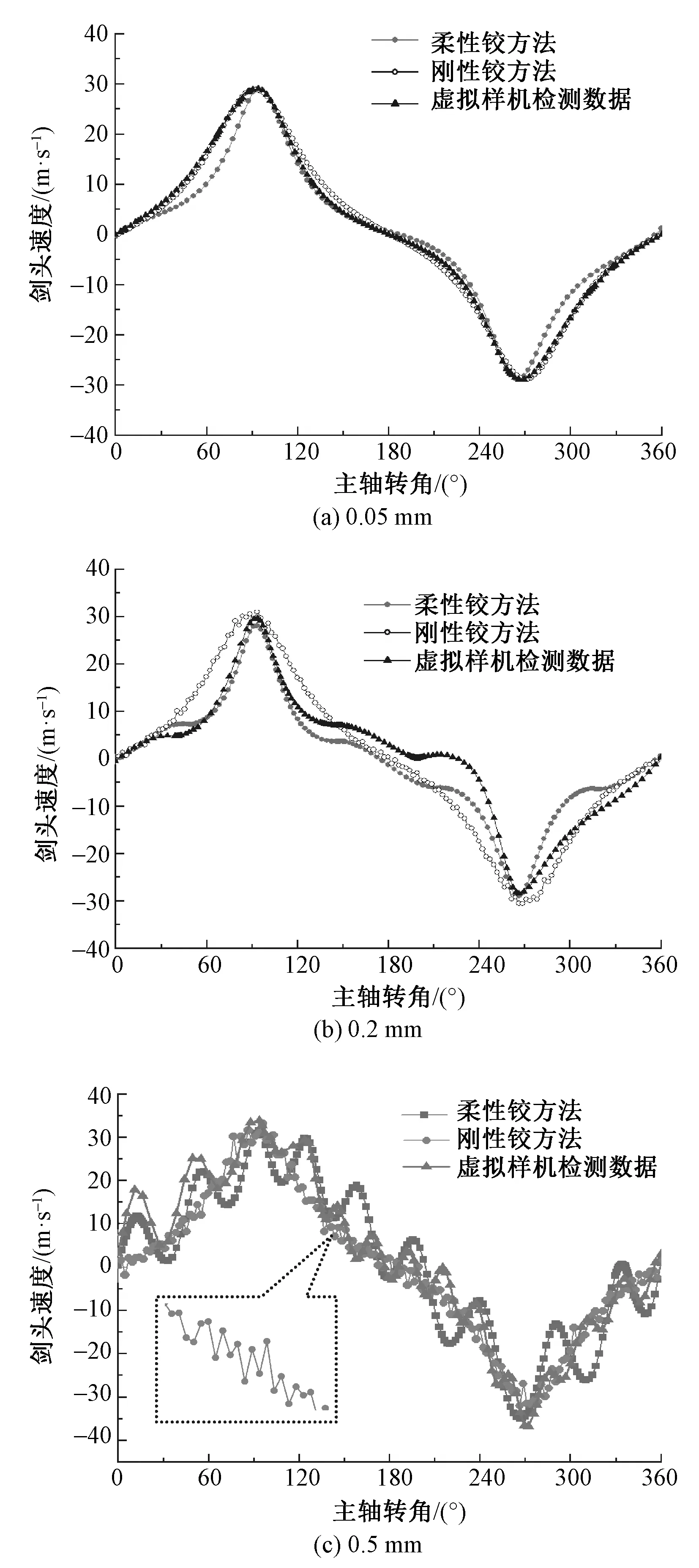
圖8 不同間隙劍頭速度曲線對比

其次對加速度曲線進行對比，結果如圖9所示。當間隙值為0.05 mm時，柔性鉸方法和剛性鉸方法以及虛擬樣機檢測數據的曲線軌跡重合度較高；當間提高到0.2 mm及以上時，柔性鉸方法和虛擬樣機檢測數據無論從最大幅值還是從運動軌跡上仍然保持了較高重合度，而此時的剛性鉸方法則呈現全周期無規律不連續振蕩，如果以剛性鉸方法求解較大間隙值下的劍頭加速度特性并將其作為判斷引緯成功率的依據，則會出現較為明顯的偏差。

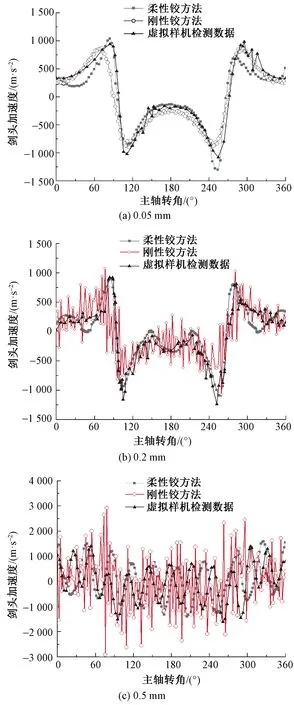
圖9 不同間隙劍頭加速度曲線對比

接下來，對劍頭位移曲線進行對比，如圖10所示。

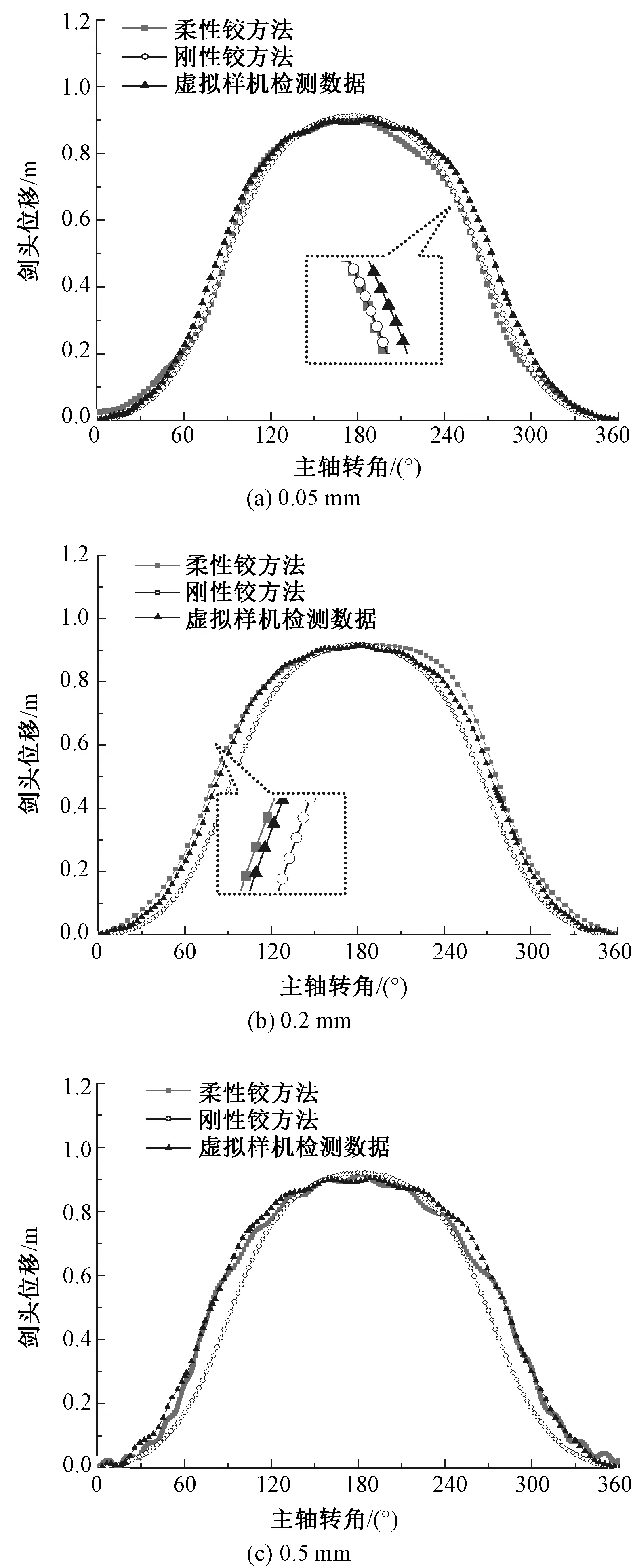
圖10 不同間隙劍頭位移曲線對比

在間隙值為0.05 mm的時候，剛性鉸方法和柔性鉸方法具有較高的重合度(見局部放大圖)，2種方法的位移曲線在劍頭送紗和回程階段中與虛擬樣機檢測數據存在一定偏差；當間隙值繼續增加到0.2 mm時，柔性鉸方法與虛擬樣機檢測數據的曲線出現了較高的重合度(見局部放大圖)，僅在主軸轉角220°～265°區間內，即緯紗交接后期與回程階段前期存在小范圍偏差；當間隙值繼續提升到0.5 mm時，柔性鉸方法和虛擬樣機檢測數據的劍頭位移曲線均出現了一定程度的波動，且重合度進一步提升，而此時的剛性鉸方法曲線仍然較為平滑，與虛擬樣機檢測數據的偏差也進一步增大。

最后，對劍頭位移誤差幅值進行對比，如圖11所示。

隨著間隙值的提高，劍頭位移的誤差值在不斷增加，且柔性鉸方法與虛擬樣機檢測數據的曲線重合度隨間隙值的增加而提升；在引緯機構運行過程中，劍頭誤差峰值均出現在主軸轉角93.6°與266.4°左右，這2個角度分別對應緯紗開始交接與引、接緯劍頭分離；在0.05 mm間隙的時候，2種方法對于誤差計算的準確度相差不大，而當間隙增加至0.2 mm時，在主軸轉角85.431°時，柔性鉸方法的劍頭誤差幅值為12.76 mm，剛性鉸方法為47.27 mm；在主軸轉角275.618°時，柔性鉸方法的劍頭誤差幅值是31.48 mm，剛性鉸方法為102.93 mm,結果見表3所示。剛性鉸劍頭誤差幅值分別是柔性鉸的3.70倍和3.27倍。隨著間隙增加到0.5 mm，柔性鉸方法與虛擬樣機檢測數據的誤差曲線呈現出相同的趨勢和更高的重合度，能夠更為準確地判斷引緯機構在引緯運動中的穩定性。

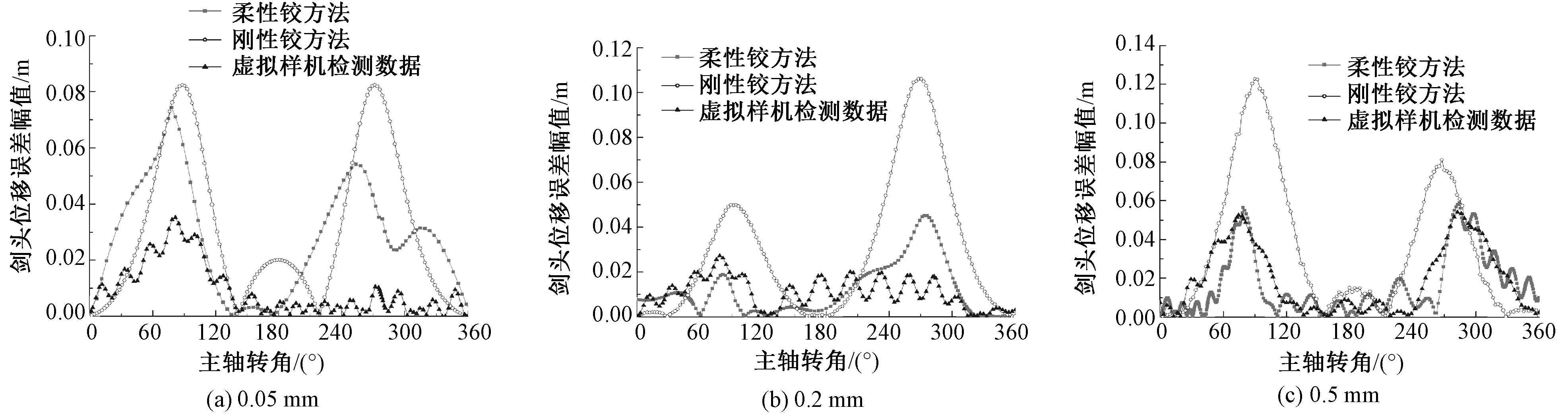
圖11 不同間隙劍頭位移誤差幅值曲線對比

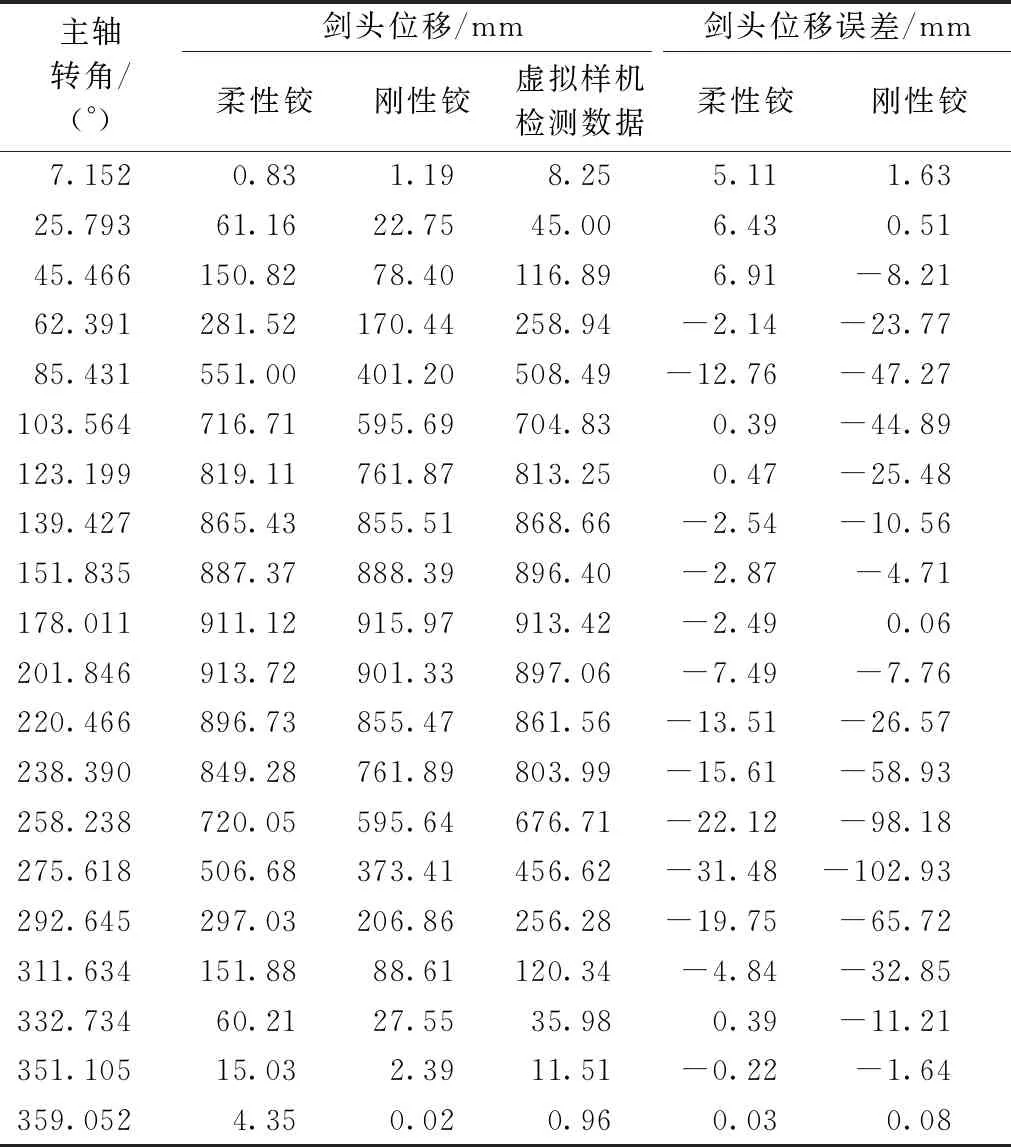
表3 劍頭位移及誤差對比(間隙0.2 mm)

5 結 論

本文將Lankarani-Nikravesh碰撞力模型嵌入到空間連桿引緯機構的動力學方程中，探討間隙對于系統動態輸出各項參數的影響，尤其是對于劍頭位移誤差的影響，對比虛擬樣機檢測數據，得到以下結論。

1)應用矢量法對間隙進行描述并求解機構的運動學特性，在計及柔性鉸間隙作用機制的前提下，選取間隙偏心距分量和機構輸出角為廣義坐標，采用Newton-Euler方法建立動力學模型，模型包含間隙碰撞過程中系統的各項動態參數。

2)結合工程實例，研究間隙對引緯工藝的具體影響。當間隙持續增加時，劍頭速度、加速度、接觸碰撞力呈現全周期大范圍波動，較為顯著地影響了緯紗交接和紗線再次進入梭口過程中的穩定性。

3)通過與剛性鉸方法及虛擬樣機檢測數據的對比，驗證了本文建模方法的準確性。同時，通過分析間隙對劍頭位移峰值誤差的影響可知，當間隙到達0.5 mm及以上時，柔性鉸方法具有更高的計算精度。