壓裂車高彈聯軸器的選型與匹配分析

彭海巖，龐強宏，劉瓊

壓裂車高彈聯軸器的選型與匹配分析

彭海巖1，龐強宏1，劉瓊2

（1.四川大學 機械工程學院，四川 成都 610041； 2.成都航空職業技術學院 機電工程學院，四川 成都 610100）

為了研究高彈聯軸器在壓裂車作業過程中對車臺上柴油發動機型號是否匹配、以避免兩者發生共振，本文在指定柴油發動機的情況下對高彈聯軸器的選型及匹配進行研究分析。首先對高彈聯軸器進行理論選型計算，然后對選出來的高彈聯軸器建立三維模型，并導入ANSYS中對其進行靜力學分析模態分析，得到其前10階固有頻率與主振型。然后在模態分析基礎上，再對其進行諧響應分析，得到其加速度、位移變形及應力響應曲線，根據其諧響應曲線結果分析可知，該高彈聯軸器對應的危險激振頻率段為0～110 Hz、危險頻率點為21 Hz和39 Hz。通過對高彈聯軸器的靜態及動態分析，使得所選擇的高彈聯軸器變得更加可靠和安全，也為今后對用于壓裂車的高彈聯軸器提供了結構設計思路和優化理論依據。

壓裂車；高彈聯軸器；模態分析；諧響應分析

目前常規油氣田開發已無法滿足人們對能源的需求，全球油氣開采開始由淺層向深層、陸地向海洋快速發展[1-2]。隨著國內對煤層氣、頁巖氣資源的開采以及原有油氣田挖潛增產措施的不斷推進，大型數控壓裂車在各油田得到廣泛應用，同時壓裂設備作業能力也需要不斷提升。柴油機在壓裂作業過程中不僅是主要的動力來源，也是主要的激振源，因此為了降低柴油機的輸出振幅，需要在柴油機與變速箱之間加一個具有減振性能的高彈聯軸器。常規的高彈聯軸器根據彈性元件的不同可分為金屬高彈聯軸器和非金屬（橡膠）高彈聯軸器，相對于金屬彈性元件，橡膠具有更好的阻尼性能，位移補償能力大，可以補償軸線的徑向位移、軸向位移和角度位移，且經濟性好[3]，所以在壓裂車上越來越多地采用橡膠材料的高彈性聯軸器，主要是為了調整軸系固有頻率和降低其扭振振幅來改善軸系的扭振特性、衰減其振動傳遞、改善軸系對中性能、提高輸出功率的穩定性。吳量等[4]在選型上通過對傳動轉矩理論計算和對壓力及工作壽命校核來進行聯軸器的選型，吳東闖[5]主要是針對最大轉矩與理論轉矩進行聯軸器的選型計算，但都沒有考慮聯軸器是否會與系統設備發生共振。因此為了合理選用壓裂車上的高彈聯軸器，不僅要進行理論方面選型計算，也應該考慮所選聯軸器的自身固有頻率是否會與其連接設備發生共振。

1 高彈聯軸器減振參數及理論選型

1.1 高彈聯軸器的減振性能參數

在壓裂車上車臺上的傳動系統中，高彈聯軸器在減振性方面主要起兩方面作用[6]，一方面可以調節整個傳動系統中振動的固有頻率，另一方面可以降低扭轉振動中的振幅。高彈性聯軸器主要通過對質量、剛度及轉動慣量的調節來控制傳動系統的固有頻率；然后通過對質量、動態剛度、轉動慣量及阻尼的調節來控制傳動系統中的振動振幅；因此可以得出調節控制高彈性聯軸器在傳動系統中的主要參數為質量、動態剛度K、相對阻尼、轉動慣量。

1.2 高彈聯軸器的理論選型計算

壓裂車選用柴油機MTU-16V4000S83，16缸4沖程的V型布置，相關參數如表1所示。

表1 柴油機及變速箱相關信息

變數箱主動端轉動慣量J為：

J＝J1＋J2

變速箱負載轉動慣量J為：

J＝J1＋J2

負載額定轉矩為[7]：

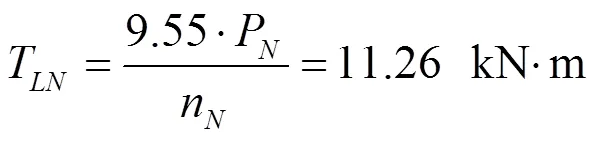
式中：J2為高彈聯軸器主動端的轉動慣量，kg·m2；J2為高彈聯軸器從動端的轉動慣量，kg·m2；P為額定功率，kW；n為額定轉速，r/min。

主動端在起動或轉速工況變化時出現的周期性沖擊轉矩峰值為：

T＝2T

（1）按額定轉矩校核選型情況：

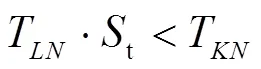
（2）按主動端沖擊計算：

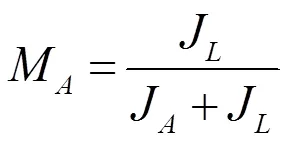
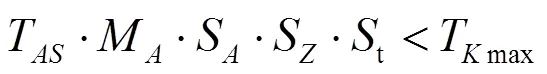
式中：S為溫度系數，S＝1.4；T為額定轉矩，N·m；M為主動端的減振系數；；S為主動端的沖擊扭轉系數，對于一般的起動沖擊可取1.8；S為起動系數，工作溫度＝50℃、S＝1.4、起動次數≤60次/h時S＝1.0；Tmax為最大轉矩，N·m。

根據主動端沖擊計算，最大轉矩小于Reich AC11型高彈聯軸器的最大轉矩，安全。AC11高彈聯軸器主要信息如表2所示，外觀形狀如圖1所示。考慮所選聯軸器的自身固有頻率是否會同與其連接設備發生共振,需要進行有限元分析。

表2 AC11高彈聯軸器主要信息

圖1 Reich AC 11外觀視圖

2 高彈聯軸器有限元分析

利用ANSYS軟件，對高彈聯軸器在給定轉矩工況下進行靜力學分析、模態分析及諧響應分析，為今后專門設計適合壓裂車高彈聯軸器提供設計思路及設計方法。根據理論選型計算，初步選出適合該壓裂車合適的高彈聯軸器型號Reich AC 11。

2.1 高彈聯軸器的三維模型建立

Reich AC 11結構如圖2所示，利用三維制圖軟件SolidWorks建立了該高彈聯軸器的三維模型，如圖3所示。

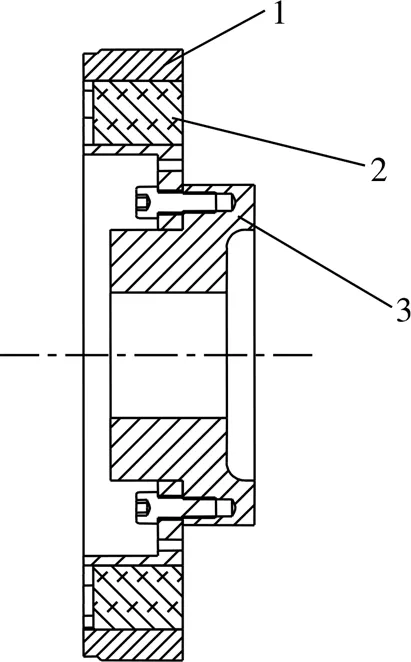
1.外法蘭盤 2.彈性橡膠體3.鎖緊套

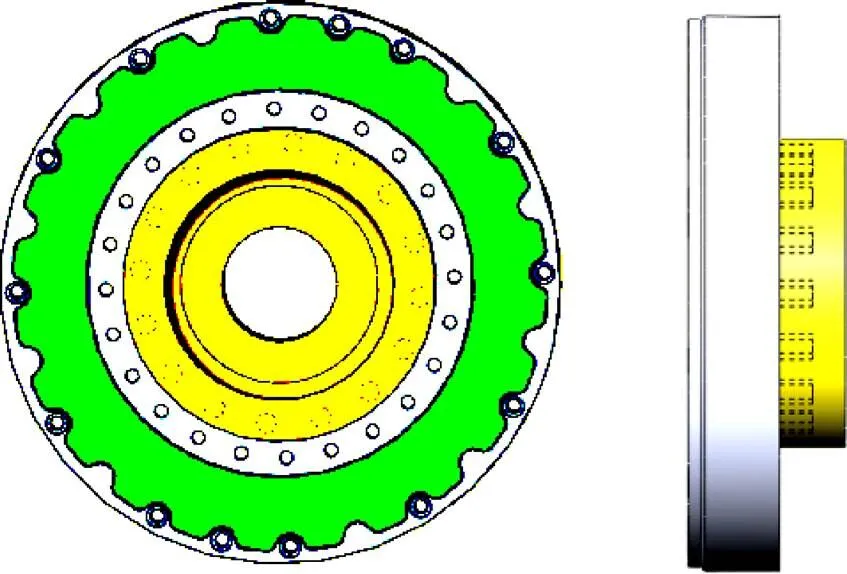
圖3 高彈聯軸器三維模型

2.2 高彈聯軸器線性靜力學分析

通過線性靜力分析，可以找到高彈聯軸器的主要結構在額定工況下其零部件的變形和材料應力的最大值及分布情況。

2.2.1 線性靜力學分析理論基礎

線性靜力學分析主要是用來分析結構在給定靜力作用下的靜力載荷響應，其經典力學理論動力學公式[8]為：

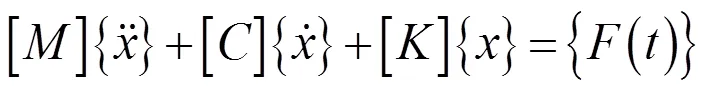
式中：[]為質量矩陣；[]為阻尼矩陣；[]為剛度系數矩陣；{}為位移矢量；{()}為力矢量。

2.2.2 高彈聯軸器靜強度有限元分析

（1）材料參數及網格劃分

外法蘭盤和鎖緊套采用45鋼，密度7850 kg/m3，彈性模量2.1×105Pa，泊松比0.31；彈性體采用橡膠，密度1800 kg/m3，彈性模1.4×106Pa，泊松比0.48。

高彈聯軸器模型網格劃分如圖4所示，共劃分了321649個單元格、803853個節點。

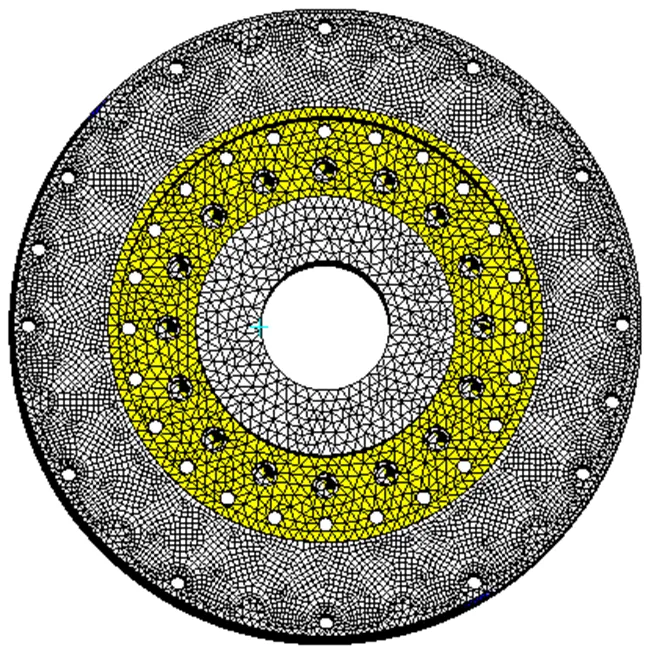
圖4 高彈聯軸器模型網格劃分

（2）模型邊界條件的定義

彈性橡膠體部分與外法蘭之間采用綁定約束，這樣可以避免在施加大轉矩時橡膠體齒處出現大變形、從而導致有限元分析報錯而無法繼續；橡膠體與其連接的金屬元件硫化固結在一起，因此也進行綁定約束；與橡膠體固結在一起的金屬盤與鎖緊套時通過螺釘固結在一起，因此在有限元分析時進行綁定連接，在加載時將鎖緊套的內表面進行固定，然后沿著外法蘭表面上施加扭轉載荷。

（3）靜強度有限元分析結果

根據高彈聯軸器的應力與應變云圖（圖5、圖6）可以看出，高彈聯軸器所受最大應力點在法蘭的表面。

2.3 高彈聯軸器的模態分析

ANSYS求解模態分析的方法有子空間法、分塊Lanczos法、縮減法、非對稱法、阻尼法、QR阻尼法、Power Dynamics法等。在ANSYS軟件中進行模態分析主要用于確定結構的振動特性，如各階的固有頻率和各階的振型，了解結構的固有頻率和振動形式，從而避免在使用中由于共振的因素造成不必要的損失[9]。并且通過模態分析得到的結果主要取決其結構的本身特性及材料屬性，與外界激勵沒有關系。

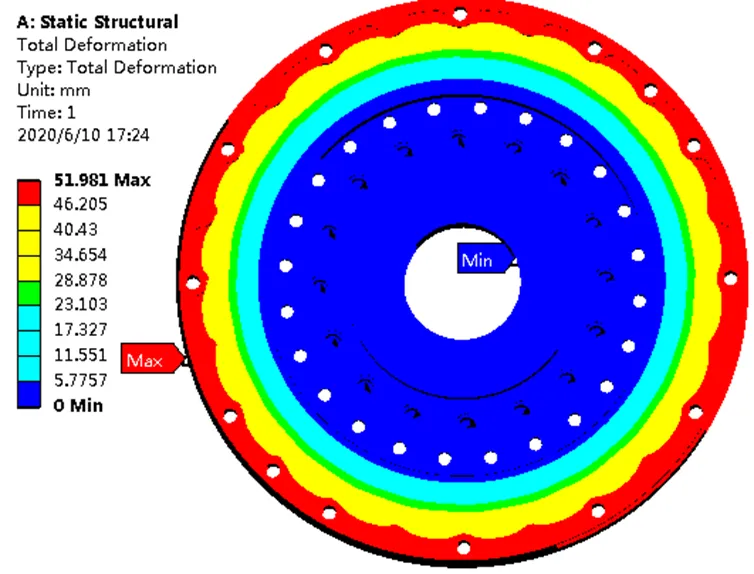
圖5 高彈聯軸器的應力云圖

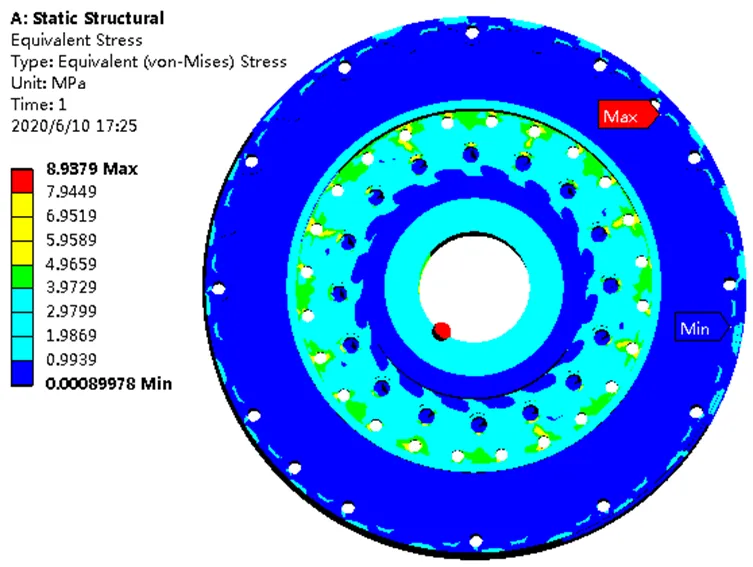
圖6 高彈聯軸器的應變云圖

2.3.1 模態分析計算理論基礎

模態可用自由振動的微分方程來分析，其中無阻尼自由振動方程為[10]：

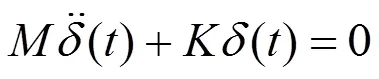
式中：為剛度矩陣、系統的質量矩陣；()為系統單元位移量。

令()為一個簡諧函數，然后帶入式（6），因無阻尼自由振動應有非零解，則有：

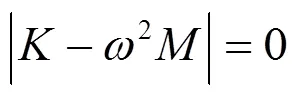
式中：1,2, …, ω為系統的固有振動頻率，Hz。

式（7）為多自由度體系中的自由振動頻率方程，求解該方程即可得到所建立模型的固有振動頻率。

本項目所采用的柴油發動機的往復慣性力所產生的激振頻率計算公式為[11]：

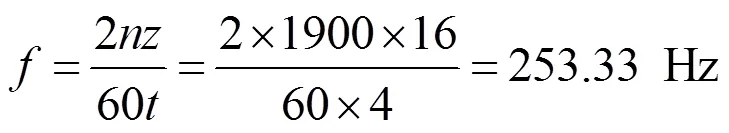
式中：為發動機額定轉速，r/min；為發動機缸數；為發動機沖程數。

2.3.2 高彈聯軸器的整體模態分析

為使高彈聯軸器整體不與柴油發動機發生共振，利用有限元分析對高彈聯軸器整體進行模態分析，結果如表3所示。可以看出，高彈聯軸器整體的固有頻率都能避開壓裂車柴油機的激振頻率（253.3 Hz），說明選擇的高彈聯軸器類型能夠很好地避免傳動系統共振問題。

通過對高彈聯軸器整體的前10階模態分析，可以得到相應的振型，由于7、8、9、10階振型基本與第6階振型基本相似，因此僅展示其前6階振型，如圖7所示。可以發現各階頻率下的振動形態，高彈聯軸器在低頻時外法蘭的邊緣振動比較大，而高頻時振動主要集中在外法蘭和部分彈性體的上并且呈對稱分布。

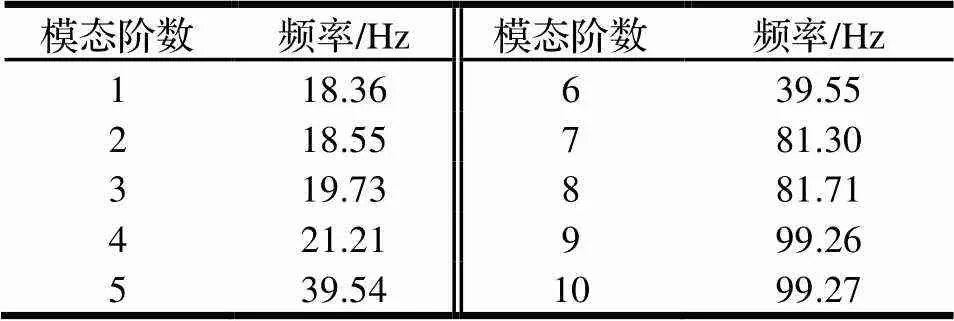
表3 各階模態下高彈聯軸器的固有頻率

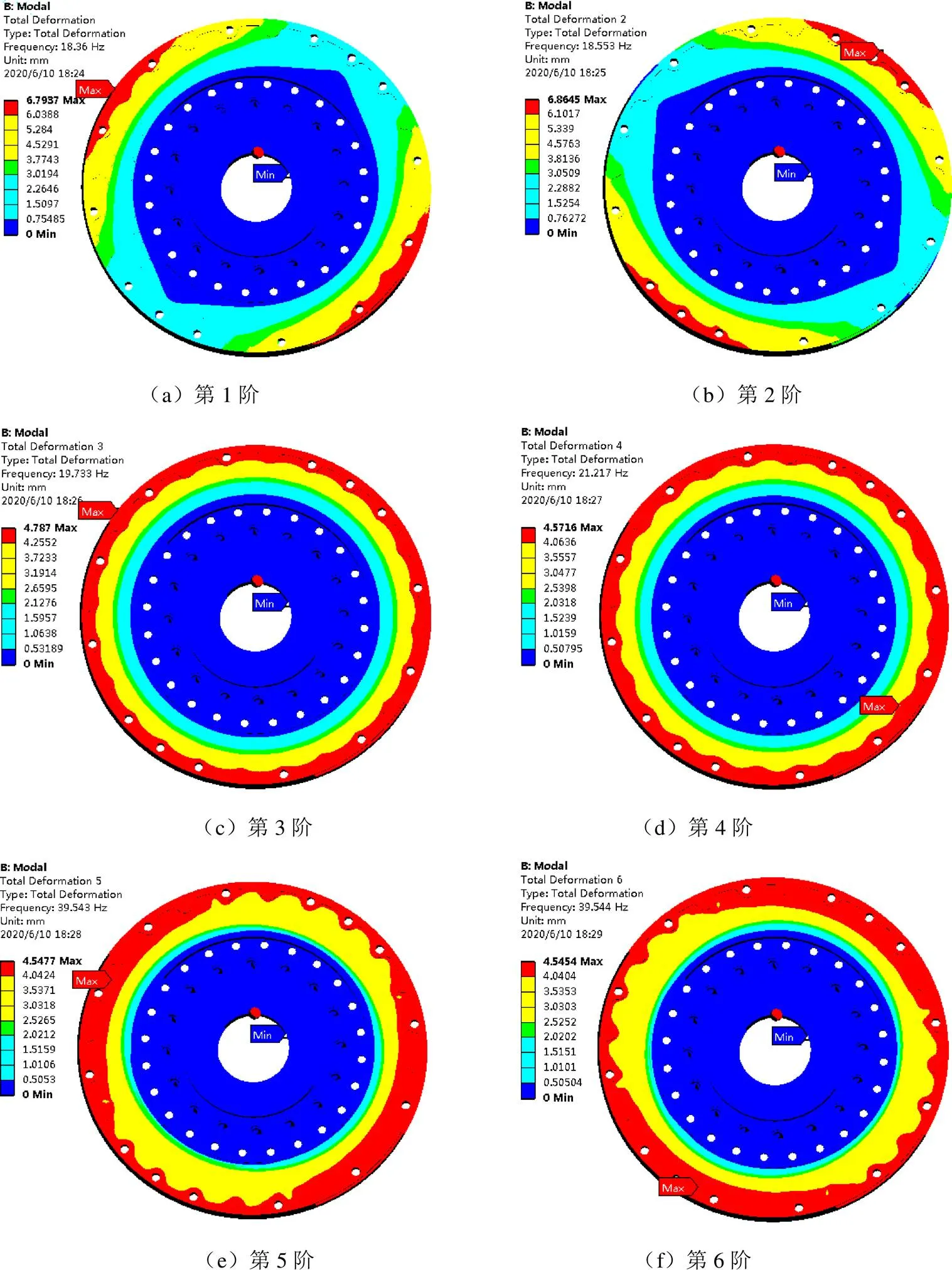
圖7 高彈聯軸器前6階模態主振型

2.4 高彈聯軸器的動態分析

對于高彈聯軸器的動態分析，主要是以諧響應分析為主。諧響應分析是用于確定線性結構在承受隨時間按正弦（簡諧）規律變化的載荷時的穩態響應，分析過程中只計算結構的穩態受迫振動，不考慮激振開始時的瞬態振動，這樣只需計算出其結構在幾種不同頻率下的響應值（位移變形、應力、加速度），目前諧響應的求解方法主要有完整法、縮減法及模態疊加法，而模態疊加法是以上求解方式中最快的方法，因此在高彈聯軸器模態分析的基礎上使用模態疊加法。作為諧響應求解的基本方法，然后根據求解結果繪制出其響應值－頻率曲線圖，通過對曲線圖形的分析不僅可以預測高彈聯軸器機構的動力特性，而且還可以用于驗證高彈聯軸器的結構是否能避免由外界激勵所導致的共振及其他受迫振動等有害因素[12]。

2.4.1 諧響應分析基礎理論

對于簡諧振動先假定一個簡諧形式解為：

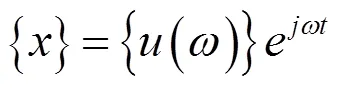
式中：()為復位位移量；為虛數單位；為角頻率，Hz；為時間，s。

對式（9）進行一階和二階求導可得：

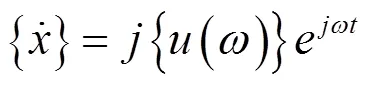
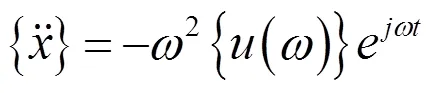
將以上公式代入經典動力學公式（4）并簡化可得：

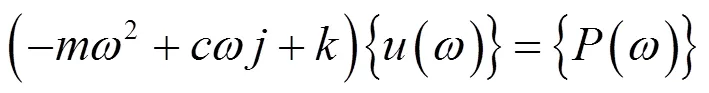
如需要對阻尼或外載有相位角考慮，則該表達式即代表復系數方程系統。利用復數算法對于每一個輸入激勵的頻率的運動方向近似靜力學方程一樣進行求解[13]。

2.4.2 高彈聯軸器的諧響應分析

利用ANSYS系統中的諧響應分析功能在已知模態情況下進行諧響應分析求解，首先設置對高彈聯軸器外法蘭表面施加繞中心軸的轉矩大小為11224 N，然后設置掃頻范圍為0～100 Hz，最后對加速度、位移變形及應力的諧響應進行求解，結果如圖8～圖11所示。

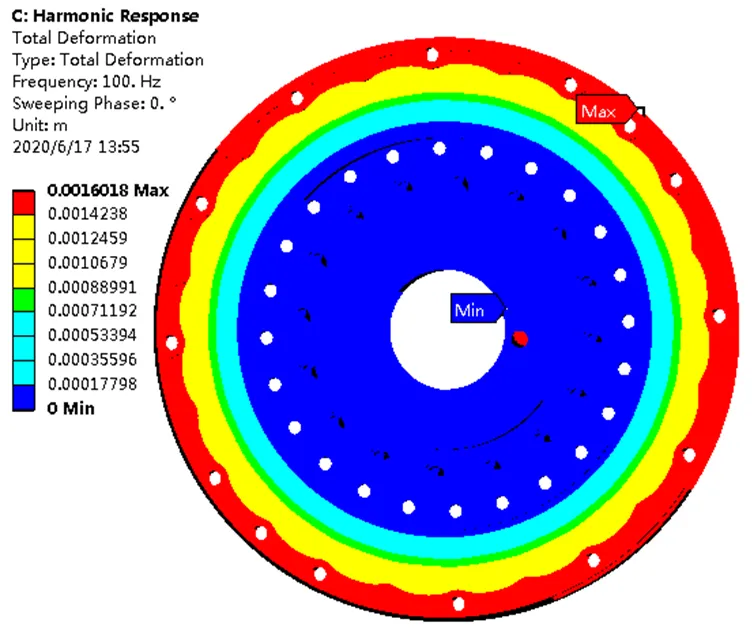
圖8 高彈聯軸器諧響應總變形云圖

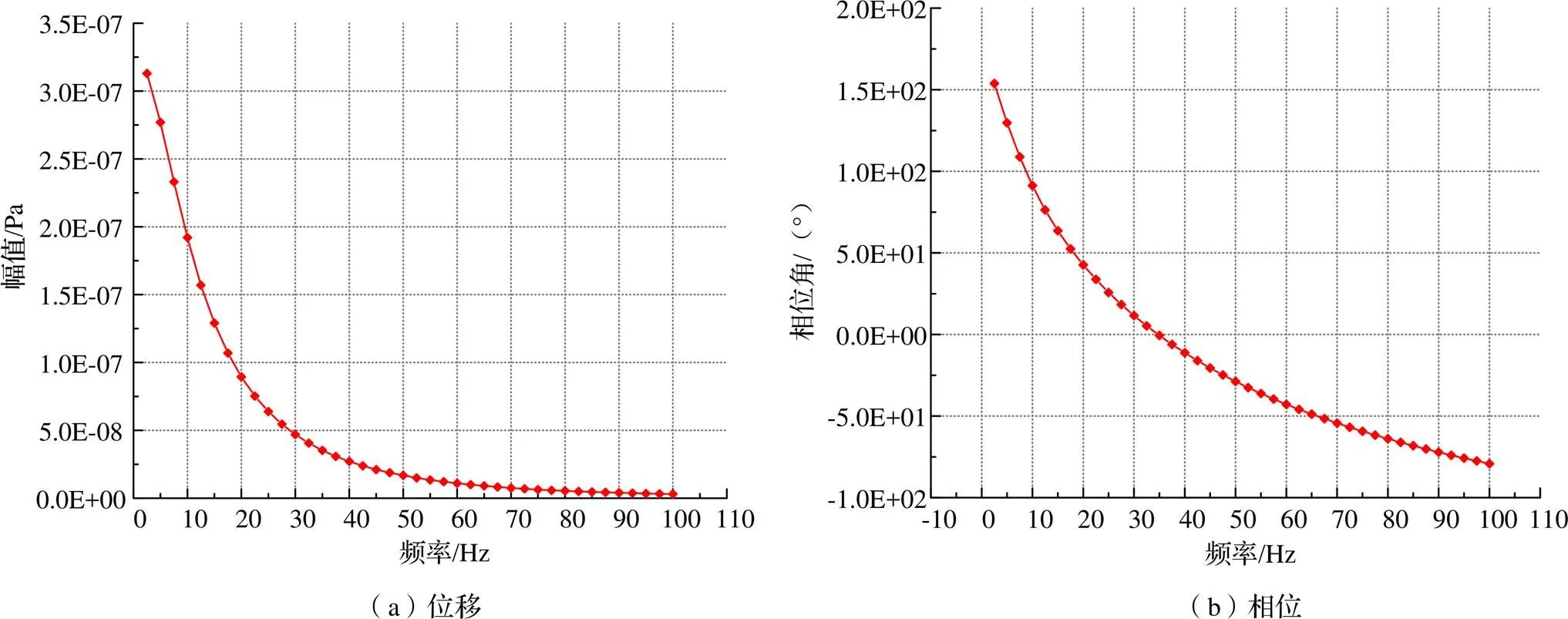
圖9 高彈聯軸器位移幅值及相位圖

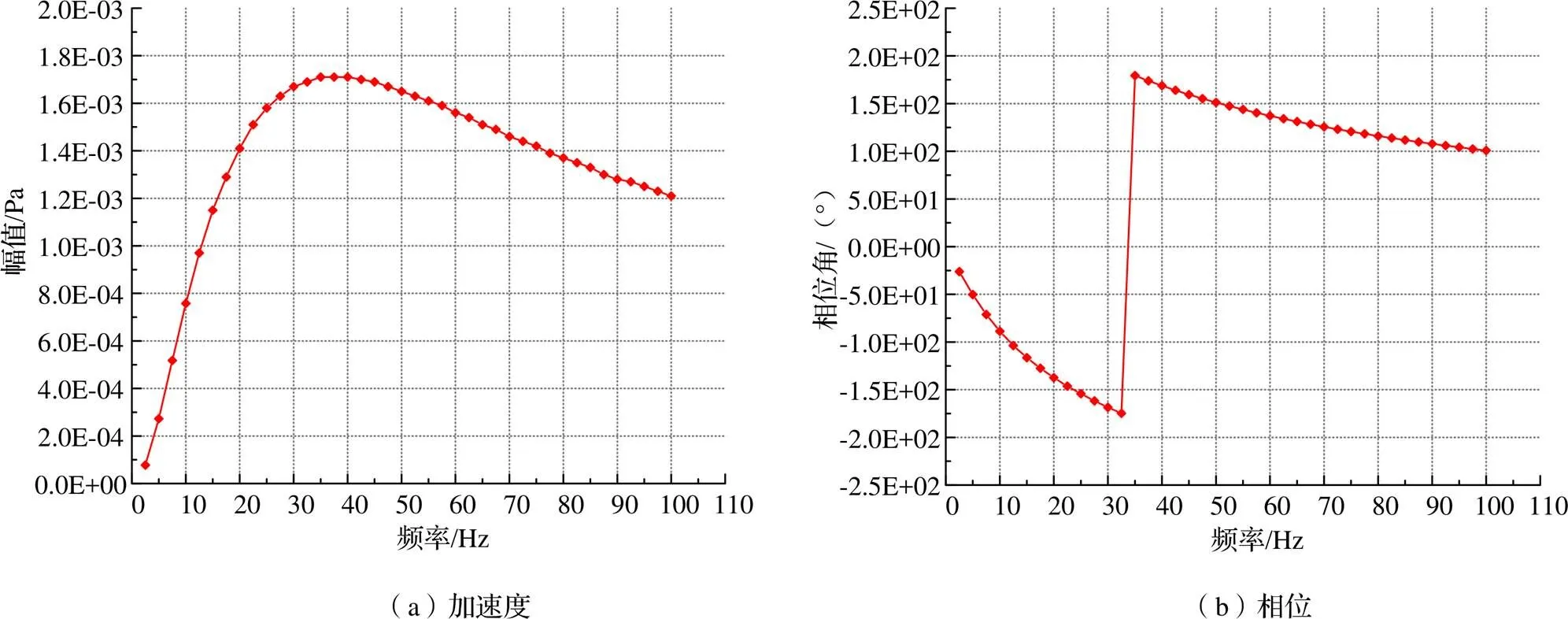
圖10 高彈聯軸器加速度幅值及相位圖

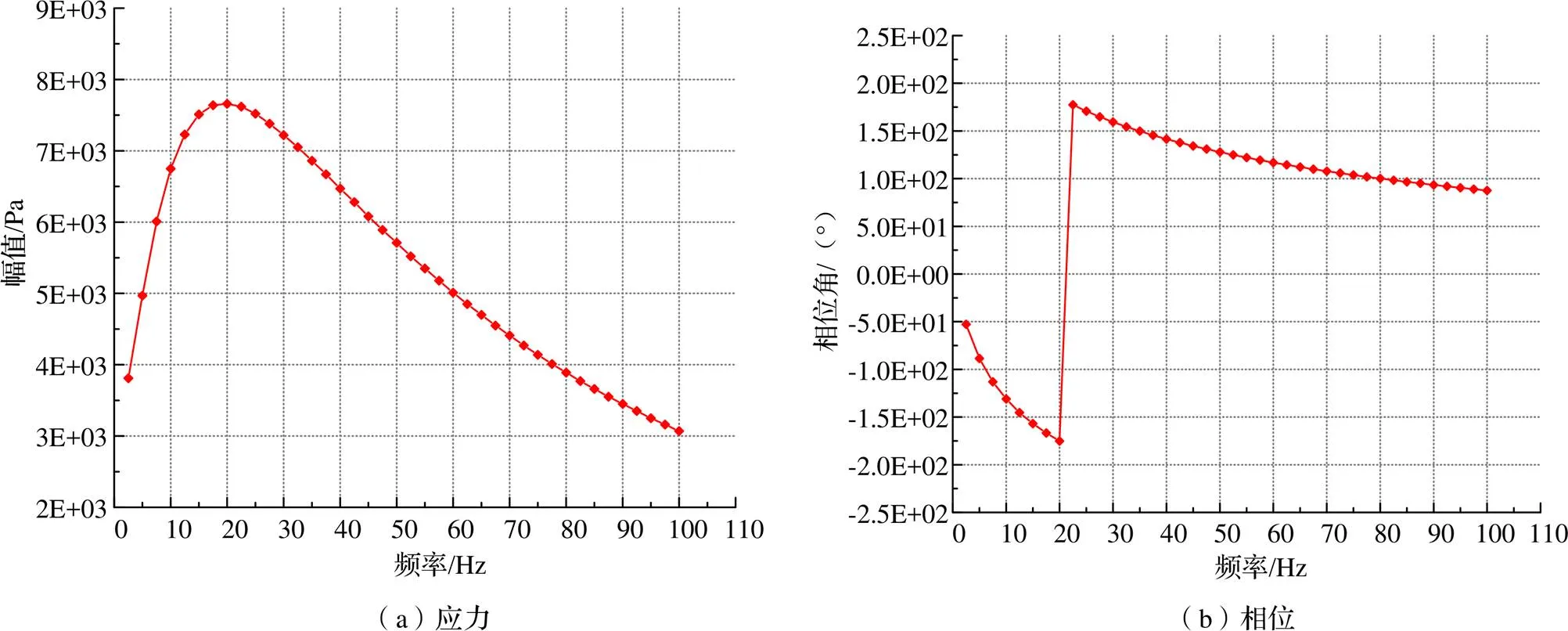
圖11 高彈聯軸器應力度幅值及相位圖

由圖8～圖11的分析結果可以看出，該高彈聯軸器在低頻時對幅值的影響較大，隨著頻率的逐漸升高其變形量趨于定值。通過加速度和應力分析可以看出，其危險在頻率21 Hz和39 Hz，有應力、加速度2個指標響應量的峰值；頻率100 Hz時出現最小應力響應，頻率110 Hz時出現最小變形量及加速度響應波谷。根據以上分析可以得知，高彈聯軸器對應的危險激振頻率段為0～110 Hz。

前面計算了項目使用的MTU-16V4000S83柴油發動機輸出的激振頻率值約為253.3 Hz，在柴油發動機啟動從0 r/min加速度到額定轉速1900 r/min時間短，能很快地越過高彈聯軸器的低頻共振區間。因此可以得出AC 11高彈聯軸器不會與MTU-16V4000S83柴油發動機發生共振，能滿足其動態要求。

3 結論

根據理論選型計算初步確定了高彈聯軸器的型號為ARCUSAFLEX-AC 11，然后以該型號的高彈性聯軸器為研究對象，進行了高彈性聯軸器三維建模、靜強度有限元分析、模態分析及動態特性計算分析研究，得到如下結論：

（1）通過額定轉矩和沖擊轉矩的理論計算表明，選用ARCUSAFLEX-AC 11高彈聯軸器能保證壓裂車的正常運用。

（2）采用有限元法可以較方便地得到高彈性聯軸器的靜動態特性參數，通過模態分析能夠知道其固有頻率以及主振型，清晰地得到高彈聯軸器固有頻率的變化趨勢。

（3）在模態分析的基礎上進行諧響應分析，根據分析結果可知，該型號的高彈性聯軸器滿足該柴油機載荷下的強度要求，能夠有效避免與柴油機產生共振，并且還確定了該高彈聯軸器的危險頻率為21 Hz和39 Hz。

該項目研究結果可為壓裂車高彈性聯軸器與柴油發動機的選型與匹配提供選型理論依據和技術支撐，也為今后專門設計適合壓裂車高彈聯軸器提供了設計思路以及設計方法。

[1]張大權，張家強. 中國非常規油氣勘探開發進展與前景[J]. 資源科學，2015，37（5）：1069-1074.

[2]翟光明，王世洪，何文淵. 近十年全球油氣勘探點趨向與啟示[J]. 石油學報，2012，33（增刊1）：14-19.

[3]謝華銀，侯天柱. LS1210型高彈性聯軸器疲勞壽命預測[J]. 柴油機，2019，41（3）：37-39.

[4]吳量，胡覺凡. 液壓安全聯軸器的選型計算[J]. 重型機械，2016 （4）：85-89.

[5]吳東闖. KWGP無極繩絞車聯軸器的選型計算與改進[J]. 煤炭與化工，2016，39（8）：114-115.

[6]姜小熒，周文建. 高彈性聯軸器振動特性試驗方法研究[J]. 柴油機，2012，34（5）：40-41.

[7]趙之鐵，褚洪森. 淺談橡膠高彈性聯軸器選用、計算[J]. 價值工程，2015，33（5）：136-137.

[8]劉巖強. 理論力學[M]. 2版. 東營：中國石油大學出版社，2002：275.

[9]韓勇，馬詠梅. 基于ANSYS二次橡膠減振器的模態分析[J]. 機械設計與制造，2010，63（3）：63-65.

[10]莫麗，黃崗. 2500型五缸壓裂泵整機模態分析及結構優化[J]. 石油機械，2012，40（7）：67-69.

[11]劉忠硯，劉健. 壓裂車重載隔振器性能分析與系統仿真[J]. 石油機械，2016，41（4）：76-81.

[12]鄭彬，鐘發. 鼓式制動器模態及諧響應分析[J]. 中國農機化學報，2020，41（4）：118-122.

[13]李斌華. 激光陀螺捷聯慣組減震系統設計及其動力學研究[D]. 長沙：國防科技大學，2008.

Selection and Matching Analysis of High Elastic Coupling of Fracturing Truck

PENG Haiyan1，PANG Qianghong1，LIU Qiong2

(1.School of Mechanical Engineering, Sichuan University, Chengdu 610041, China;2.College of Mechanical and Electrical Engineering,Chengdu Vocational and Technical College of Aviation, Chengdu 610100, China)

In order to study whether the high-elastic coupling matches the diesel engine model on the platform during the fracturing vehicle operation and to avoid resonance between the two, this article selects and matches the high-elastic coupling under the condition of specified diesel engine. First, the theoretical selection calculation of the high-elastic coupling is carried out, and then a three-dimensional model is established on the selected high-elastic coupling. ANSYS is applied for static analysis and modal analysis, and the first 10 natural frequencies and the main frequency modes are obtained. Based on the modal analysis, the harmonic response analysis is carried out to obtain the acceleration, displacement, deformation and stress response curves. The results show that the dangerous excitation frequency corresponding to the high elastic coupling is 0~110 Hz and dangerous frequency points are 21 Hz and 39 Hz. Through the static and dynamic analysis, more reliable and safe high-elastic coupling is selected. This study provides structural design ideas and optimization theory basis for the high-elastic coupling used in fracturing vehicles in the future.

fracturing truck；high elastic coupling；modal analysis；harmonic response analysis

TE934

A

10.3969/j.issn.1006-0316.2021.02.004

1006－0316 (2021) 02－0024－08

2020－06－22

校企聯合開發項目（19H0193）

彭海巖（1989－），男，四川資陽人，碩士，主要研究方向為高彈聯軸器的振動分析，E-mail：peng13032835705@163.com。