雙石英玻璃珠的低速沖擊破碎行為

簡世豪，苗春賀，張 磊，單俊芳，王鵬飛，徐松林,2

（1. 中國科學技術大學中國科學院材料力學行為和設計重點實驗室，安徽 合肥 230027；2. 中國地震局地震預測研究所高壓物理與地震科技聯合實驗室，北京 100036）

顆粒物質在自然界中廣泛存在，并在工業生產中廣泛應用。顆粒破碎行為及其相關機制的研究在凝聚態物理、土木工程、醫藥工程、粉末技術、物流運輸等許多領域都有重要的理論和應用價值[1-3]。迄今為止，大多數研究主要集中于單個玻璃珠的破碎行為，如在Hertz 接觸理論框架下研究玻璃珠的彈性接觸剛度和有效模量[2,4]，在Weibull 分布函數框架下研究玻璃珠的彈性特性、拉伸強度和屈服強度等[2-3,5]。高速沖擊下顆粒破碎機制相對比較清楚，但中低速沖擊下顆粒破碎機制還需要進一步開展研究和探索。

顆粒動態破碎主要采用4 種實驗技術：直接撞擊[6]、輕氣炮平板撞擊[7]、雙面撞擊[8]以及利用分離式霍普金森壓桿（Split Hopkinson pressure bar，SHPB）設備[9]。低速沖擊下，球體的破碎作用力源于錐體周圍的拉伸環向應力，破碎形式主要表現為Hertzian 環和錐形裂紋。高速沖擊下，顆粒被粉碎為更細小的顆粒。Potapov 等[10]的數值分析結果表明：玻璃珠破壞存在兩種失效機制，即從接觸點開始徑向延伸變形產生的拉應力失效和垂直徑向延伸方向的橫向裂紋產生的拉伸失效。低速沖擊下的失效破壞以前者為主，高速沖擊時則為兩種失效機制共同作用。方繼松等[11]采用離散元數值模擬了單玻璃珠撞擊剛壁的過程，研究結果揭示了更加復雜的破壞形態和機理。

單顆粒破碎反映的是顆粒內部力鏈體系的演化，多顆粒破碎則可反映不同力鏈體系的鏈接與演化，對于應力狀態的波動更為敏感，可以更好地揭示實際顆粒體系的破碎機制，但目前取得的實驗結果相對較少。Parab 等[12]采用SHPB 裝置對分別由1、2、3、5 個顆粒組成的4 種鈉鈣玻璃珠群進行了沖擊加載實驗，利用高速同步輻射X 射線相襯成像技術進行原位觀測，結果表明：多顆粒體系中，裂紋從兩個顆粒間的接觸區域開始擴展；在進一步壓縮時，大量裂紋在某個顆粒中萌生，其中一個初始裂紋和新形成的子裂紋在穿過顆粒時迅速分叉，并爆炸性地將顆粒破碎成許多小碎片，而其他顆粒幾乎完好無損。Jiang 等[13]開展了兩個玻璃珠鏈的沖擊實驗，結果表明：只有小部分輸入應力波能通過雙珠鏈系統的破碎而耗散，隨著輸入能量的增加，能量耗散效率提高；摩擦耗散（特別是在嚴重破碎時）似乎總是占據主導地位。截至目前，對于顆粒沖擊破碎機制的認識仍存在較大爭議。

基于此，本研究將結合高速攝影技術對雙石英玻璃珠進行SHPB 沖擊實驗，對比單石英玻璃珠的沖擊破碎行為，探討低速沖擊下石英玻璃顆粒的破碎機制。

1 實 驗

1.1 實驗材料

實驗所用石英玻璃珠的化學組分（質量分數）為SiO2(69.13%)、B2O3(10.75%)、K2O (6.29%)、Na2O (10.40%)、BaO (3.07%)、As2O3(0.36%)。實驗樣品的直徑分別為：(8.30 ± 0.10) mm、(11.68 ± 0.16) mm、(15.42 ± 0.21) mm、(17.50 ± 0.23) mm。玻璃珠直徑的相對偏差在1.4%以內，較均勻。計算中采用樣品的實際尺寸。

1.2 沖擊實驗

沖擊壓縮實驗在SHPB 裝置上進行。實驗裝置如圖1 所示，子彈長30 cm，入射桿和透射桿的長度均為100 cm，直徑均為14.50 mm。為保證有足夠長的脈寬，在入射桿端部添加足夠大的整形器，使加載波上升沿變緩。為保證實驗的可重復性，在試件與桿之間加入碳化鎢墊片。

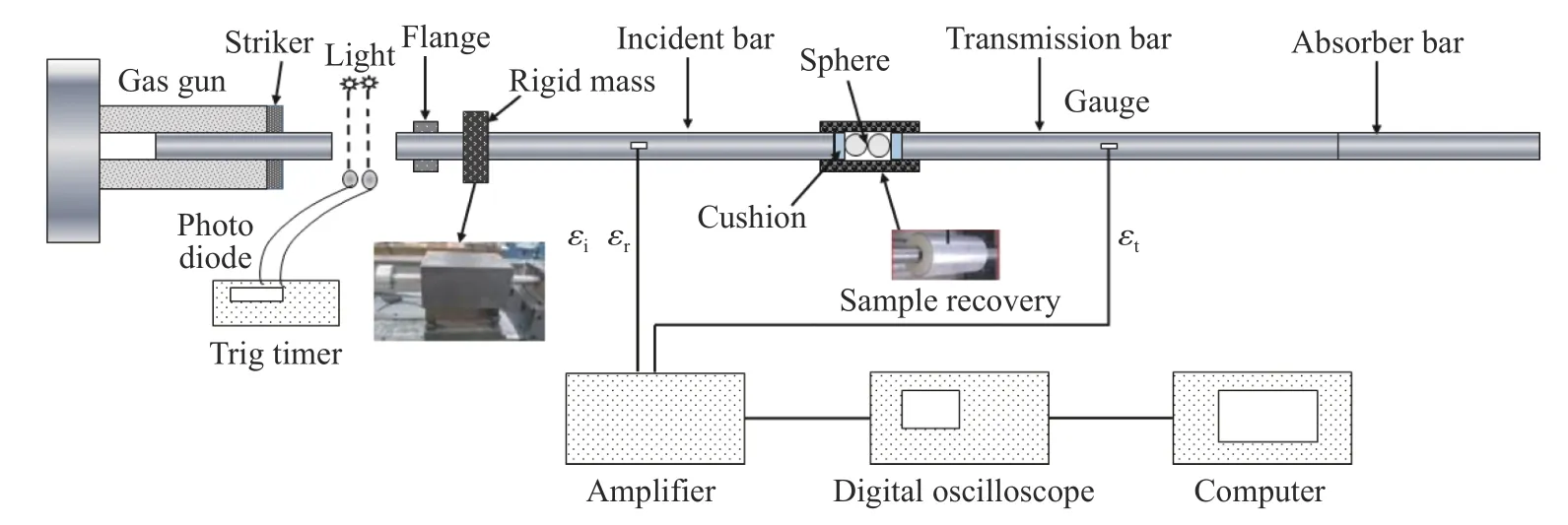
圖1 SHPB 實驗裝置Fig. 1 Schematic diagram of the modified SHPB device

沖擊速度較低時，球體內不會出現破碎現象；沖擊速度足夠高時，球體會被撞擊粉碎；并且存在一個球體破碎的臨界速度。直徑為8.30、11.68、15.42、17.50 mm 的玻璃球，其臨界破碎沖擊速度分別為(3.4 ± 0.1) m/s、(5.6 ± 0.2) m/s、(6.7 ± 0.4) m/s、(8.0 ± 0.4) m/s[3]，此時試樣保持完整和破碎的概率均為50%。因此，結合嘗試實驗的結果確定本實驗條件如下：對直徑為8.30 mm 的玻璃珠分別開展速度為5.6、7.0、9.0 m/s 的沖擊實驗，對直徑為11.68 mm 的玻璃珠分別開展速度為6.0、7.5、9.5 m/s 的沖擊實驗，對直徑為15.42 mm 的玻璃珠分別開展速度為6.5、9.5、11.5 m/s 的沖擊實驗，對直徑為17.50 mm 的玻璃珠分別開展速度為7.5、9.5、11.5 m/s的沖擊實驗。每個沖擊速度下，均開展5 次以上重復實驗，選取重復性較好的3 次結果進行分析。

在開展動態實驗的同時，使用Phantom V12.1 高速相機進行全程跟蹤拍攝，在相機前放置有機玻璃板對鏡頭進行保護。動態實驗中幀間隔為14 μs，畫幅分辨率約為240 × 150 像素。實驗中使用兩個2 000 W 新聞燈提供足夠亮的光源。對于不需要拍攝的實驗，采用兩個塑料袋分別套封玻璃珠，以便同時收集兩個玻璃珠的沖擊破碎產物。破碎產物的統計先采用篩分法進行質量百分比統計，然后選取尺度在1 000 μm以下的顆粒，采用合肥工業大學材料測試中心的激光粒度分析儀Mastersizer 2000 進行體積百分比統計。

1.3 沖擊過程瞬態紅外測溫

紅外測溫技術（Infrared temperature measurement system, ITMS）是一種快速獲取試樣表面實時溫度的有效方法。劉永貴等[14]、單俊芳等[15]分別對沖擊下的鈦鎳合金和花崗巖進行了瞬態紅外測溫，形成了較可靠的實驗技術；Guo 等[16]、Jiang 等[17]進一步采用多點瞬態紅外測溫技術分別研究了金屬的熱塑失穩和陶瓷的脆性破裂機制。本研究采用相同的測試裝置，結合沖擊過程進行玻璃珠試樣的局部瞬態測溫，具體實驗裝置布局如圖2 所示。瞬態紅外測溫系統主要包括：紅外探測器、鍍金凹面鏡、前置放大器、斬波器、直流電源等。沖擊作用下，試件內部由于塑性變形、破碎、相變等變化產生輻射能，這些輻射能通過聚焦凹面鏡匯聚到探測器內的光敏單元上，轉化為電信號后傳輸到示波器上并進行記錄。由于測溫系統對外界變化非常敏感，因此每次動態實驗之前都要對系統進行原位溫度標定。

圖2 結合紅外測溫的SHPB 實驗裝置Fig. 2 Modified SHPB with ITMS

實驗采用Judson 公司生產的4 單元HgCdTe 紅外測溫系統，設備型號為MCT-Q-1。測點尺寸為1 mm × 1 mm，測點間距0.05 mm，響應時間約0.5 μs。測點定位如圖2 所示，由于有兩個測點信號非常弱，實驗時只取兩個信號較強的測點，每次實驗前采用激光光源進行測點位置確定。其他參數可參見文獻[17]。

2 實驗結果

2.1 載 荷-位 移 關 系

沖擊過程中試樣所受的載荷一般采用三波法進行估算。這一計算方法的前提條件是試樣所受的載荷/變形基本達到均勻狀態，即試件兩端的載荷差異小于5%。但從實驗結果來看，在雙玻璃珠系試樣中很難保證此條件。文獻[3]對不同沖擊速度下4 種直徑的單個玻璃珠兩端載荷的差異性進行了實驗統計，結果表明：沖擊過程中，兩端載荷差異性隨沖擊速度/直徑的增大而增大。直徑17.50 mm 的試樣在應變率為400 s-1時，差異性達到9.0%～12.4%。雙玻璃珠系試樣兩端的載荷差異性同樣隨著沖擊速度/直徑的增大而增大，其變化規律與單玻璃珠相似，但載荷差異幅值比單玻璃珠試樣大1 倍。后面討論的情況是在相應的載荷非均勻性基礎上進行的，為了說明問題，以透射載荷作為參考。

圖3 為作用在試樣上的透射載荷-位移關系曲線。直徑分別為8.30 和11.68 mm 的雙玻璃珠系試樣的透射載荷-位移關系曲線均呈現出明顯的雙峰結構，表明試樣經歷了兩次壓縮過程。低速沖擊時，第1 個峰的幅值較低，第2 個峰的幅值較高；隨著沖擊速度的增大，第1 個峰的幅值迅速增大，第2 個峰的幅值增加相對較緩慢，與第1 個峰的發展相關聯。

直徑為15.42 和17.50 mm 的雙玻璃珠系試樣的透射載荷-位移關系曲線隨沖擊速度增大時的變化相對復雜。低速沖擊時，透射載荷-位移曲線呈現出明顯的雙峰結構；隨著沖擊速度的增大，透射載荷-位移曲線逐漸呈現出單峰結構。這種變化趨勢反映了尺寸效應和加載速率效應在脆性材料破壞過程中的耦合作用。下面將結合回收產物的分布特征和高速攝影結果進行綜合分析。

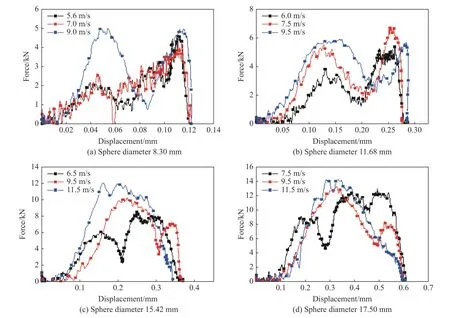
圖3 透射載荷-位移關系曲線Fig. 3 Transmitted load vs. displacement curves

2.2 破碎產物分布特征

實驗中將帶封口的尼龍收集袋分別套在兩個玻璃珠上來實現沖擊過程碎片的獨立收集。低速沖擊下，玻璃珠的破碎主要有3 種形式：形成層片狀碎片的錐形劈裂、形成較長裂紋面的中心劈裂以及形成細小顆粒的粉碎性破壞，3 種形式的破碎產物均在回收樣品中大量存在。圖4 為雙玻璃珠系試樣沖擊破碎產物的質量百分比分布，對同一次沖擊中兩個玻璃珠的碎片分別進行統計，“front”表示與入射桿接觸的玻璃珠，“back”表示與透射桿接觸的玻璃珠。由圖4 可知：玻璃珠的碎片分布與前后位置、加載速度以及玻璃珠直徑均有關聯；低速沖擊下破碎產物的質量百分比分布不適用Weibull 分布函數描述。原因在于：此沖擊速度范圍比臨界破碎速度略高，顆粒破碎機制相對復雜，有局部剪切破壞、局部拉伸破壞等多種破壞模式，破碎形態多樣化，且較大尺寸碎片的產生具有一定的偶然性。

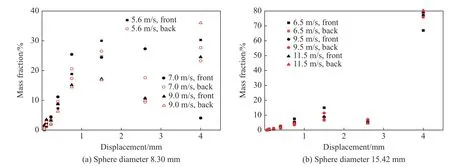
圖4 破碎產物質量分布曲線Fig. 4 Mass distribution of fragmentation products

在上述破碎產物中篩選顆粒直徑小于2.5 mm 的部分進行激光粒度分析，統計結果如圖5 所示。由圖5 可知，細小顆粒的體積百分比滿足Weibull 分布函數。對于直徑為8.30 mm 的雙玻璃珠系試樣：在5.6 m/s的沖擊速度下，前端玻璃珠的碎片尺寸比后端的大；隨著沖擊速度增大，前后端玻璃珠的破碎尺寸分布逐漸接近；沖擊速度為9.0 m/s 時，后端玻璃珠的破碎尺寸比前端略大。對于直徑為15.42 mm 的雙玻璃珠系試樣：在6.5 m/s 的沖擊速度下，前端玻璃珠的碎片尺寸比后端的小；隨著沖擊速度增大，前后端玻璃珠的破碎尺寸分布逐漸接近，但后端玻璃珠的破碎尺寸始終比前端略大。直徑11.68 mm 的試樣與直徑8.30 mm 的試樣相似，直徑17.50 mm 的試樣與直徑15.42 mm 的試樣相似。產生差異的原因在于：試樣中前后端玻璃珠所受載荷不同，沖擊過程中后端所受載荷比前端高；同時，玻璃珠的截面積沿沖擊方向先逐漸變大，而后逐漸變小，對局部剪切引起的破碎擴散過程有一定的影響，即直徑越大，對破碎擴散過程的限制越強。這也使得應變率越高，局部應變梯度越大。

圖5 細顆粒產物的體積分布曲線Fig. 5 Volume distribution of finer particle products

3 低速沖擊下玻璃珠的破碎機制分析

3.1 高速攝影下的破碎發展過程

圖6 為單個玻璃珠沖擊破碎過程中的高速攝影圖像[3]。單個玻璃珠的沖擊破碎源于玻璃珠兩端接觸部位局部的Hertz 裂紋擴張（圖6(a)中紅色圈出部分）。隨著沖擊過程的進行，此部分逐漸擴散，有一個明顯的擴散界面，往玻璃球中部發展，其傳播速度隨玻璃球破碎截面面積的增大而減小，平均約320 m/s。當傳播速度減小到一定程度（例如50 m/s，甚至更小）時，Hertz 裂紋界面逐步穩定下來，同時，在玻璃珠中部產生貫穿球體的斜直裂紋。這種斜直裂紋的發展很快，從產生到結束不超過15 μs（圖6(b)中綠色圈出部分），其產生源于垂直沖擊方向的側面拉伸破裂。

雙玻璃珠體系反映出沖擊速度和玻璃珠尺寸會影響前端和后端玻璃珠的破碎次序和破碎程度。圖7 為直徑11.68 mm 的雙玻璃珠體系沖擊破碎過程中的高速攝影圖像，對應的沖擊速度為9.09 m/s。單個玻璃珠的沖擊壓縮反映了與圖6 相同的破碎過程。圖7(a)、圖7(b)、圖7(c)中主要是接觸部位Hertz 裂紋破碎區的發展；圖7(d)中Hertz 裂紋破碎區逐漸停止發展，玻璃珠內部產生貫穿的斜直裂紋系；圖7(e)、圖7(f)中入射端玻璃珠先發生破碎，隨后反射端的玻璃珠破碎。

圖6 單顆粒沖擊破碎（箭頭為沖擊方向）[3]Fig. 6 Images of single sphere failure under impact(The arrow denotes the impact direction)[3]

圖7 雙玻璃珠系的沖擊破碎（箭頭為沖擊方向）Fig. 7 Images of double spheres failure under impact (The arrow denotes the impact direction)

將高速攝影結果與透射載荷-位移曲線進行對比發現，第1 個波峰與入射端玻璃珠的破碎程度對應良好，第2 個波峰與反射端玻璃珠的破碎程度對應良好。對4 種直徑的雙玻璃珠系分別進行3 種沖擊速度下的高速攝影分析，結果表明：低速沖擊時(如6.0 m/s)，反射端的玻璃珠先破碎，入射端的玻璃珠后破碎；隨著沖擊速度逐漸增大，反射端和入射端的玻璃珠幾乎同時破碎；當速度增大至一定值時(如9.0 m/s)，入射端的玻璃珠先破碎，反射端的玻璃珠后破碎。其原因在于：桿的波阻抗比玻璃珠高，對雙玻璃珠系后端所受的載荷有反射增強作用；低速沖擊時，雖然入射端玻璃珠沒有破碎，但是后端玻璃珠由于反射應力增強而發生破碎。高速沖擊時，前端玻璃珠直接發生沖擊破碎。

因此，中低速沖擊時玻璃珠的破碎是以接觸部位的Hertz 裂紋的擴散過程為先導，而后誘導產生貫穿玻璃珠的斜直裂紋系。前期以局部剪切變形為主，后期以側向拉伸破壞為主。這使得玻璃珠的沖擊破碎機制較復雜，Weibull 強度統計規律也需要作出相應的改變[3]。

3.2 瞬態紅外溫度的發展過程

圖8 所示為直徑11.68 mm 的單個玻璃珠沖擊過程中的紅外溫升歷程。圖8 中藍色曲線為透射載荷-時間曲線，將其在圖中列出以便與溫升過程進行對比。沖擊速度為5.98 m/s 時，玻璃珠沒有發生破碎，圖8(a)中所示玻璃珠的壓縮過程有較小幅度的紅外溫升，約為0.3 ℃。壓縮過程結束后，沒有明顯的溫升。這說明壓縮過程有微小的破裂存在，壓縮過程終止時，微小破裂停止發展。此過程中的溫升可基于應力-應變關系曲線，結合塑性功-熱能轉換原理進行理論計算[17]。理論溫升值（TAl-T0）的計算公式為

沖擊速度為7.41 m/s 時，玻璃珠發生破碎，圖8(b)顯示玻璃珠的壓縮過程有較大幅度的紅外溫升，壓縮過程終止時，兩個測點的溫升分別為0.5 和0.9 ℃，反映出壓縮過程局部破裂的差異。壓縮過程終止后，兩個測點均有較小幅度的溫升，表明局部微小破裂仍有發展。當沖擊速度達到9.28 m/s 時，玻璃珠嚴重破碎，圖8(c)顯示玻璃珠的壓縮過程在大幅度的溫升之后，溫度存在一定程度的降低，最后穩定在約1 ℃。初期的大幅度溫升表明局部嚴重破裂，輻射出較高的紅外能；而后發生較小規模的穩定破裂，輻射穩定的紅外能。更高速度的沖擊與其規律相似，但是兩個測點的差異會更大。壓縮過程終止時，兩個測點均保持較高水平的溫升，表明即便沒有外載荷作用，較大的破裂仍在發展。

圖8 沖擊產生的局部紅外溫升Fig. 8 Local infrared temperature rise generated during impact

脆性材料的沖擊破碎至少包含兩種機制：只在壓縮過程導致“塑性溫升”的微小破裂和在壓縮過程結束后仍導致溫升的宏觀破裂。文獻[17]利用較規則的氮化硼試樣，對兩種機制的溫升進行了分離。本研究中的試樣形態不利于進行此類分離。比較3 種沖擊速度下破裂的發展過程，發現破碎界面的發展存在一種破碎擴散阻力，當沖擊速度達到一定幅值后，外載荷作用促使內部破碎擴散阻力超過其閾值，動態破碎過程可以自主完成。本實驗中，此臨界破碎擴散阻力介于5.98～7.41 m/s 的沖擊速度之間。雙玻璃珠系的溫升具有更復雜的形態，本次不進行討論。

3.3 沖擊破碎擴散過程的控制方程

石英玻璃沖擊破碎陣面的產生與初始加工缺陷和剪切作用有關[18]，由此，Feng[19]提出了一種剪切激活的擴散方程，用剪切引起的孔隙體積Vd作為擴散變量來描述破碎陣面的傳播

式中：t、x 分別為時間坐標和縱坐標，D、f 分別為損傷體積擴散和損傷體積驅動函數。損傷體積擴散函數表示為

式中： s(x,t)=(Y(x,t)－YF)/(YHEL－YF)； 擴散系數 λ 為材料參數；應力偏量， σxx和 σyy分別為縱向和側向應力；YHEL和YF分別表示無損材料在Hugoniot 彈性極限和損傷材料在完全失效狀態下的應力偏 量。損傷體積驅動函數表示為

式中：參數 td為 給定縱向位置的損傷演化特征時間，只有當 Vd＞Vd0和 Y ＞YTHD時損傷體積驅動演化才能被激活（Vd0和YTHD分別表示應力偏量閾值和膨脹體積臨界值）。

Jiang 等[17]基于此思想，結合高速攝影全場應變演化采用等效剪應變( εe)作為擴散變量研究了六方氮化硼材料中破壞陣面的傳播。本研究對象為玻璃珠，樣品幾何形態比上述研究要復雜得多，需要考慮截面變化的影響。由此，可初步得到剪切激活的擴散方程（圖9 所示，其中xf為破碎陣面的位置）為

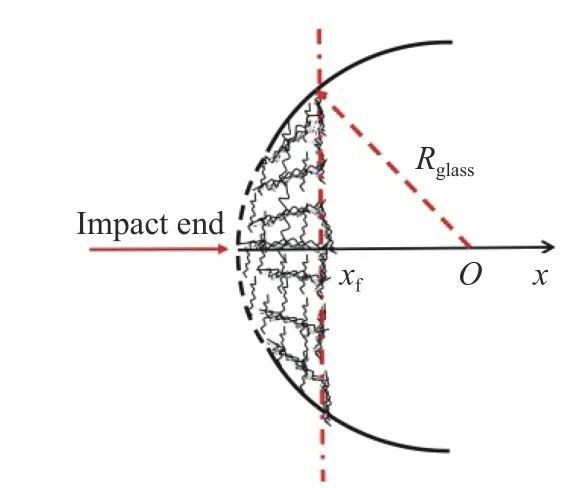
圖9 破碎陣面Fig. 9 Failure wave front

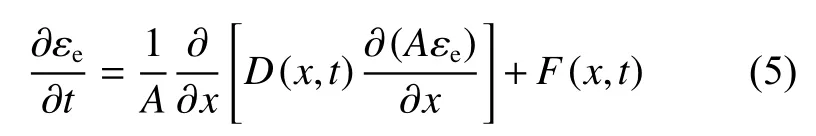
其中

式中： εeTHD為 局部失效的臨界剪應變； τd為材料參數；YM為玻璃珠試樣的極限強度；A 為x 處的截面面積 ，。局部破碎試樣的壓縮行為可近似描述為

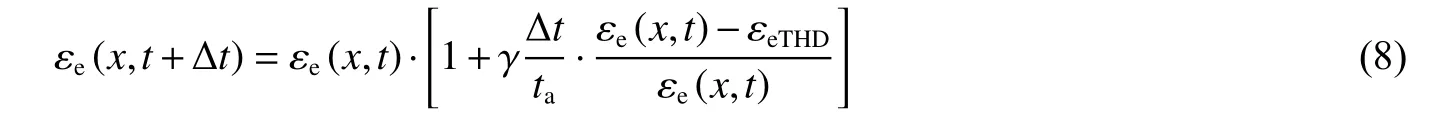
式中： Δt 為時間增量； ta為與脈沖寬度相關的時間參量； γ為激活因子，在沖擊端面略高于1.0，支撐端面略低于1.0。

此擴散分析主要用于局部的Hertz 裂紋擴張和裂紋系的擴散過程研究。

進一步確定玻璃珠中破碎陣面的終止位置，此時處于Hertz 裂紋擴張和裂紋系的擴散階段停止、準 備轉入貫穿性破壞產生階段。由 ε=ε(x,t) 和(x,t)，可得到

由此，結合式(5)、式(9)、式(10)，以及實測入射波、反射波和透射波信息，分析剪切激活的損傷擴散阻力。

4 結 論

基于高速攝影和瞬態紅外測溫技術，對4 種直徑的雙玻璃珠系進行了沖擊實驗，研究其沖擊破碎機制，得到以下主要結論。

（1）在低速沖擊下，雙玻璃珠的破碎次序隨著沖擊速度的增大，逐漸從反射端的玻璃珠先破碎過渡到入射端的玻璃珠先破碎。玻璃珠的沖擊破碎源于兩端接觸部位局部的Hertz 裂紋擴張和裂紋系的擴散，最后在玻璃珠中部產生貫穿球體的斜直裂紋而發生整體崩潰。破碎產物中直徑小于2.5 mm 的細顆粒的分布滿足Weibull 分布。

（2）瞬態紅外測溫結果表明，玻璃珠的破碎主要包含兩種機制，即只在壓縮過程導致“塑性溫升”的微小破裂和在壓縮過程結束后仍導致溫升的宏觀破裂。低速沖擊過程存在臨界破碎擴散阻力。這需要結合進一步的理論分析進行界定。