對2020年高考卷的挖掘與思考

2021-04-08 03:06:32何正文

何正文

(廣東省肇慶市百花中學 526020)

高考卷往往具有高度啟發性，本文對2020年的數學高考試卷進行分析，對高考題的考查背景、目標、意義進行解剖，對其中某幾個典型題目進行挖掘，希望對高三教學有一定的指導作用.

一、伸展高考試題變式，提高數學能力，化變形為階梯，登高望遠

例1(2020年全國Ⅰ卷理科第6題)函數f(x)=x4-2x3的圖象在點(1，f(1))處的切線方程為( ).

A.y=-2x-1 B.y=-2x+1

C.y=2x-3 D.y=2x+1

分析這是一道考查利用導數求解函數的切線方程，考查計算能力，屬于基礎題，對這道題進行深入挖掘，可以設計出下面的變式題.

變式1過點(1，-1)作曲線f(x)=x4-2x3的切線l，求直線l的方程.

變式2若直線y=-2x+m與曲線f(x)=x4-2x3相切，求m.

變式3斜率為-2的直線l與曲線f(x)=x4-2x3恰有一個、兩個、三個公共點，分別求出直線l的縱截距或其取值范圍.

變式4曲線f(x)=x4-2x3上是否存在這樣的點P，使得曲線在點P處的切線與曲線再無其余公共點？若存在，此點有何特殊性？

變式5斜率為-2的直線與曲線f(x)=x4-2x3相切于點P，并與曲線有另一交點Q，求P、Q兩點的坐標.

教師要充分挖掘試題本身的形，幫助學生找到其中的義，通過變形熟悉共性的含義，從而提高學生的數學能力.

例2(2020年全國Ⅱ卷理科第17題)在△ABC中，sin2A-sin2B-sin2C=sinBsinC.

(1)求角A；

(2)若BC=3，求△ABC周長的最大值.

本題對應(人教A版高中數學《必修5》教材習題1.2 A組(14)):在△ABC中，角A,B,C所對應的邊分別為a,b,c，求證：c(acosB-bcosA)=a2-b2.

解法同例1，利用余弦定理、正弦定理可求解出來.

反思以上高考題(17)是教材A習題(14)的異曲同工，并且均可以從正弦定理、余弦定理等角度入手.相比之下高考題(17)讓考生更加清晰.從高考題中能找到課本習題的影子，無論課本習題還是高考題，都要挖掘其背后的化歸、分類、整體數學思想.

1.化歸

這道高考三角函數題，有化歸數學思想，本質就是把未知引向已知，把陌生引向熟悉.通過不斷地變形轉換，把不熟悉、不規范、復雜的形式化歸為熟悉、規范甚至模式化、簡單的形式.

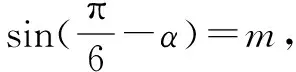
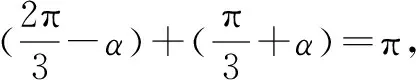
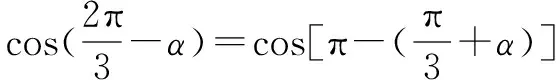
=-m.

2.分類

分類討論思想體現化整為零、積零為整兩個方面，注重條理、邏輯.能訓練學生的思維條理性和概括性，所以在高考試題中占有重要的位置.

解析(1)當n奇數時，

(2)當n偶數時，

3.整體思想

數學整體思想方法從整體結構或整體特征考慮，化繁為簡，化零為整，化難為易.

例5 已知函數f(x)=msin(πx+α)+ncos(πx+β)(m,n,α,β為非零實數),且f(2009)=-1，求f(2010)的值.

分析直接求出系數m,n比較困難,不妨利用誘導公式和已知考察f(2009)和f(2010)的關系再進行求解.

解析因為f(2009)=msin(2009π+α)+ncos(2009π+β)=msin(π+α)+ncos(π+β)=-msinα-ncosβ=-(msinα+ncosβ)=-1，

所以msinα+ncosβ=1.

故f(2010)=msin(2010π+α)+ncos(2010π+β)=msinα+ncosβ=1.

點評注意整體思想的應用.解答本題的關鍵就是求得式子asinα+bcosβ=1(整體)，它是聯系已知和未知的紐帶.

例6(2020年全國Ⅰ卷理科第17題)設{an}是公比不為1的等比數列，a1為a2，a3的等差中項．

(1)求{an}的公比；

(2)若a1=1，求數列{nan}的前n項和．

這道題的難點在第(2)問，此題讓我想起了一道課本習題：求和S=1+2x+3x2+…+nxn-1(人教版必修5第61頁).

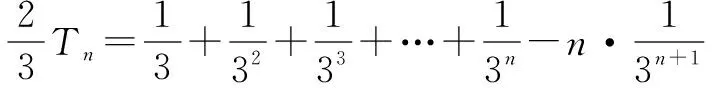
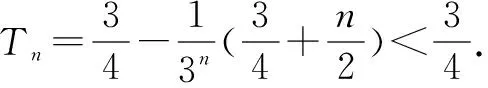
如果我們跳出這道題的慣性解法，不用錯位相減法求和呢？

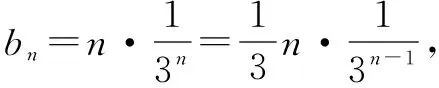
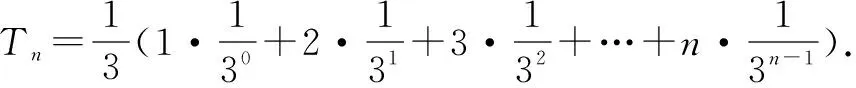
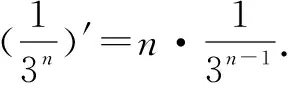
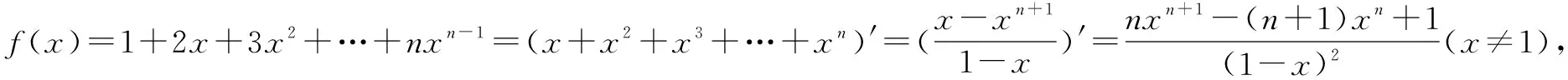
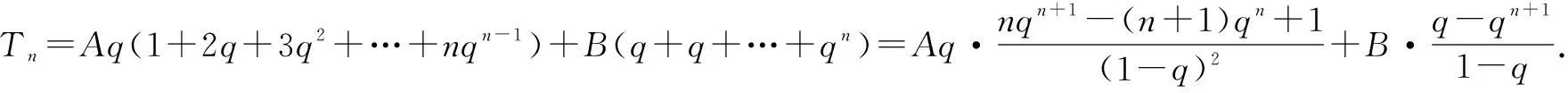
這是我們跳出了數學思維定勢，挖掘題目后面的本質.數學思維是今年高考突出考查的重點.

今年的高考題型特點是少陷阱、少套路，淡化刷題性價比.多注重數學思想，多側重數學思維，強化實踐性的應用.教師要培養學生的應用數學能力，注重數學思維養成，數學知識結構的完善.這是筆者對今年高考題的認識，希望能給高三教師同行們一些啟發，更希望幫助更多的高三學子更好備考，做到事半功倍，舉一反三.