細看近八年高考中的排列組合試題

武增明

(云南省玉溪第一中學 653100)

從2009年開始，全國多數省市使用新課標，2012年，全國多數省市根據新課標考綱命制高考數學試題，所以筆者想到細看2012年至2019年全國各省市高考試題中的排列組合試題.高考題凝聚著眾多命題專家的心血，是命題專家智慧的結晶.深入研究歷年高考試題是科學復習備考的有效途徑.排列和組合是高中數學學習中一個很特別的內容，它對學生提出了較高的分析問題和解決問題能力的要求，是培養學生思維的一個重要場所.排列組合問題是高考常考題，縱觀近八年高考試題，多數排列組合試題難度不大，大部分題型都是以選擇題和填空題的形式出現，但題型多樣，解題思路獨特，方法靈活，考生普遍感到困難，失分現象嚴重.為此，本文對近八年全國各省市高考中的排列組合試題進行分類例析，以揭示其求解規律.這些高考題不僅為一線教師的教學提供了豐富的教學資源和很強的教學導向，也可成為高三同仁在2021年高考備考教學復習中具有很大參考價值的第一手資料，同時希望能對2021年乃至今后幾年挑戰高考的考生有所啟示和幫助.

一、排列問題

例1 (2012年高考四川卷理科數學第11題)方程ay=b2x2+c中的a，b，c∈{-3，-2，0，1，2，3}，且a，b，c互不相同.在所有這些方程所表示的曲線中，不同的拋物線共有( ).

A. 60條 B. 62條 C. 71條 D. 80條

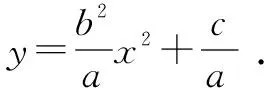
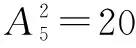
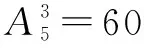
綜上所述，滿足題意的不同的拋物線有14+48=62條，故選B.

例2 (2012年高考全國卷理科數學第11題)將字母a，a，b，b，c，c排成三行兩列，要求每行的字母互不相同，每列的字母也互不相同，則不同的排列方法共有( ).

A. 12種 B. 18種 C. 24種 D. 36種

例3 (2012年高考北京卷理科數學第6題)從0，2中選一個數字，從1，3，5中選兩個數字，組成無重復數字的三位數，其中奇數的個數為( ).

A. 24 B. 18 C. 12 D. 6

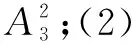
例4 (2013年高考全國大綱卷理科數學第14題)6個人排成一行，其中甲、乙兩人不相鄰的不同排法共有____種(用數字作答).

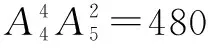
例5 (2013年高考北京卷理科數學第12題)將序號分別為1，2，3，4，5的5張參觀券全部分給4人，每人至少1張，如果分給同一人的2張參觀券連號，那么不同的分法種數是____.

例6 (2013年高考福建卷理科數學第5題)滿足a，b∈{-1，0，1，2}，且關于x的方程ax2+2x+b=0有實數解的有序數對(a，b)的個數為( ).

A. 14 B. 13 C. 12 D. 10

解析當a=0時，符合的有(0，-1) ，(0，0) ，(0，1) ，(0，2).

當a≠0時，Δ≥0，即ab≤1，符合的有(-1，-1) ，(-1，0) ，(-1，1) ，(-1，2) ，(1，-1) ，(1，0) ，(1，1)，(2，-1) ，(2，0).

綜上，符合題意的共有13對，故選B.

例7 (2013年高考四川卷理科數學第8題)從1，3，5，7，9這五個數中，每次取出兩個不同的數分別為a，b，共可得到lga-lgb的不同值的個數是( ).

A. 9 B. 10 C. 18 D. 20

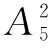
例8 (2014年高考北京卷理科數學第13題)把5件不同產品擺成一排，若產品A與產品B相鄰，且產品A與產品C不相鄰，則不同的擺法有____種.

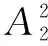
例9 (2014年高考四川卷理科數學第6題)六個人從左至右排成一行，最左端只能排甲或乙，最右端不能排甲，則不同的排法共有( ).

A. 192種 B. 216種 C. 240種 D. 288種

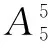
例10 (2014年高考重慶卷理科數學第9題)某次聯歡會要安排3個歌舞類節目、2個小品類節目和1個相聲類節目的演出順序，則同類節目不相鄰的排法種數是( ).

A. 72 B. 120 C. 144 D. 168

二、組合問題

例11 (2012年高考山東卷理科數學第11題)現有16張不同的卡片，其中紅色、黃色、藍色、綠色卡片各4張，從中任取3張，要求這3張卡片不能是同一種顏色，且紅色卡片至多1張，不同取法的種數為( ).

A. 232 B. 252 C. 472 D. 484

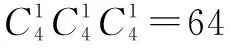
例12 (2012年高考陜西卷理科數學第8題)兩人進行乒乓球比賽，先贏3局者獲勝，決出勝負為止，則所有可能出現的情形(各人輸贏局次的不同視為不同情形)共有( ).

A. 10種 B. 15種 C. 20種 D. 30種

例13 (2012年高考課程標準卷理科數學第2題)將2名教師、4名學生分成2個小組，分別安排到甲、乙兩地參加社會實踐活動，每個小組由1名教師和2名學生組成，不同的安排方案共有( ).

A. 12種 B. 10種 C. 9種 D. 8種

例14 (2012年高考浙江卷理科數學第6題)若從1，2，3，…，9這9個整數中同時取4個不同的數，其和為偶數，則不同的取法共有( ).

A. 60種 B. 63種 C. 65種 D. 66種

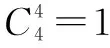
例15 (2013年高考浙江卷理科數學第14題)將A，B，C，D，E，F六個字母排成一排，且A，B均在C的同側，則不同的排法共有____種(用數字作答).

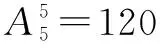
例16 (2017年高考浙江卷理科數學第16題)從6男2女共8名學生中選出隊長1人、副隊長1人、普通隊員2人組成4人服務隊，要求服務隊中至少有1名女生，共有____種不同的選法(用數字作答).

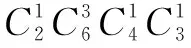
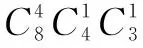
例17 (2018年高考全國Ⅰ卷理科數學第15題)從2位女生、4位男生中選3人參加科技比賽，且至少有1位女生入選，則不同的選法共有____種(用數字填寫答案).

三、排列組合問題

例18 (2012年高考重慶卷理科數學第15題)某藝校在一天的6節課中隨機安排語文、數學、外語三門文化課和其他三門藝術課各1節，則在課表上的相鄰兩節文化課之間最多間隔1節藝術課的概率為____(用數字作答).

例19 (2014年高考浙江卷理科數學第14題)在8張獎券中有一、二、三等獎各1張，其余5張無獎.將這8張獎券分配給4個人，每人2張，不同的獲獎情況有____種(用數字作答).

例20 (2018年高考浙江卷理科數學第16題)從1，3，5，7，9中任取2個數字，從0，2，4，6中任取2個數字，一共可以組成____個沒有重復數字的四位數(用數字作答).

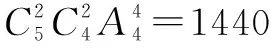
四、重復排列問題

例21 (2013年高考山東卷理科數學第10題)用0，1，…，9十個數字，可以組成有重復數字的三位數的個數為( ).

A. 243 B. 252 C. 261 D. 279

解析組成所有(有重復數字和無重復數字)三位數的個數是9×10×10=900(個)，沒有重復數字的三位數的個數是9×9×8=648(個)，所以，可以組成有重復數字的三位數的個數為900-648=252(個)，故選B.

五、重復排列組合問題

例22 (2014年高考全國Ⅰ卷理科數學第5題)4位同學各自在周六、周日兩天中任選一天參加公益活動，則周六、周日都有同學參加公益活動的概率為( ).

本題考查古典概型，實質是考查重復組合的應用.

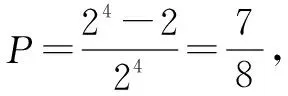
圖1

例23 (2019年高考全國Ⅰ卷理科數學第6題)我國古代典籍《周易》用“卦”描述萬物的變化.第一“重卦”由從下到上排列的6個爻組成，爻分為陽爻“——”和陰爻“— —”，圖1就是一重卦.在所有重卦中隨機取一重卦，則該重卦恰有3個陽爻的概率是( ).

解析本題考查古典概型，實質是考查排列組合的應用.

解答此題的關鍵是要清楚兩個問題：

第1個問題是，由1個陽爻“——”和1個陰爻“— —”一共可以組成多少個重卦？

這個問題的答案是2×2×2×2×2×2=26=64個.

第2個問題是，由3個陽爻“——”和3個陰爻“— —”一共可以組成多少個重卦？

故所有的重卦共有26個，其中恰有3個陽爻的重卦有20個.

評注(1)由1個陽爻“——”和1個陰爻“— —”組成所有重卦的情況是“可重復排列”的排列組合問題.(2)從下到上的每個爻都有兩種選擇，且可重復選.

六、局部平均分組分配問題

例24 (2017年高考全國Ⅱ卷理科數學第6題)安排3名志愿者完成4項工作，每人至少完成1項，每項工作由1人完成，則不同的安排方式共有( ).

A. 12種 B. 18種 C. 24種 D. 36種

解析本題是考查排列組合中的不定向分配問題.

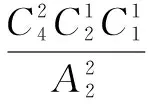
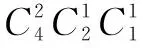
七、排列組合與概率問題

例25 (2012年高考江蘇卷理科數學第6題)現有10個數，它們能構成一個以1為首項，-3為公比的等比數列，若從這10個數中隨機抽取一個數，則它小于8的概率是____.

解析本題考查古典概型，實質是考查組合的應用.

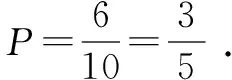
例26 (2012年高考上海卷理科數學第11題)三位同學參加跳高、跳遠、鉛球項目的比賽，若每人都選擇其中兩個項目，則有且僅有兩人選擇的項目完全相同的概率是____(結果用最簡分數表示).

解析本題考查古典概型，實質是考查組合的應用.

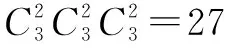
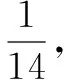
簡解本題考查古典概型，實質是考查組合的應用.

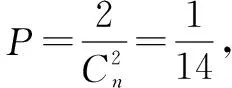
例28 (2013年高考江蘇卷理科數學第7題)現有某類病毒記作XmYn，其中正整數m，n(m≤7，n≤9)可以任意選取，則m，n都取到奇數的概率為____.

解析本題考查古典概型，實質是考查排列的應用.

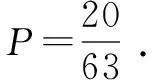
例29 (2014年高考上海卷理科數學第10題)為強化安全意識，某商場擬在未來的連續10天中隨機選擇3天進行緊急疏散演練，則選擇的3天恰好為連續3天的概率是____(結果用最簡分數表示).

簡解本題考查古典概型，實質是考查組合的應用.

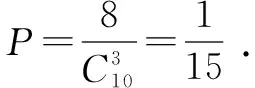
例30 (2014年高考陜西卷理科數學第6題)從正方形四個頂點及其中心這5個點中，任取2個點，則這2個點的距離不小于該正方形邊長的概率為( ).

解析本題考查古典概型，實質是考查組合的應用.

例31 (2014年高考江西卷理科數學第12題)10件產品中有7件正品、3件次品，從中任取4件，則恰好取到1件次品的概率是.

簡解本題考查古典概型，實質是考查組合的應用.

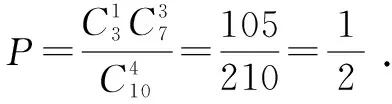
例32 (2014年高考江蘇卷第4題)從1，2，3，6這4個數中一次隨機地取2個數，則所取2個數的乘積為6的概率是____.

簡解本題考查古典概型，實質是考查組合的應用.

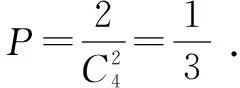
例33 (2017年高考山東卷理科數學第8題)從分別標有1，2，…，9的9張卡片中不放回地隨機抽取2次，每次抽取1張，則抽到的2張卡片上的數奇偶性不同的概率是( ).

解析本題考查古典概型，實質是考查組合的應用.

例34 (2019年高考江蘇卷理科數學第6題)從3名男同學和2名女同學中任選2名同學參加志愿者服務，則選出的2名同學中至少有1名女同學的概率是____.

簡解本題考查古典概型，實質是考查組合的應用.

說明以上例題，筆者沒有按從易到難的順序編排.

排列組合的應用問題千變萬化，學生很難摸索其規律，所以在學習中，我們一線教師應該引導學生以特殊類型為突破口，與學生一道歸納、總結一些常見模型，通過一些常見模型鞏固一些方法，拓展一些思維.常見的模型有：列舉法、直接法、間接法(剔除法、排除法)、優先法、捆綁法、分組法、插空法、插板法、投信法，這些方法在上述歷年高考排列組合試題中都體現得淋漓盡致，請讀者朋友、同學們認真加以領悟.