構建函數解不等式

顧冬梅

(江蘇省海門市第一中學 226100)

函數與方程、化歸與轉化思想是高中數學的重要思想，構建函數是這兩種思想的體現.在高中數學教學中有一類是導數與不等式相結合問題，學生感到有點棘手，本文針對常出現的三類不等式怎樣構造函數作了一點總結，希望對大家有所啟發.

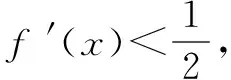
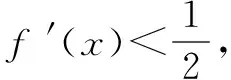
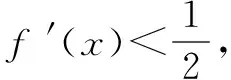
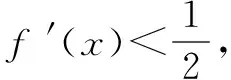
總結這類問題將導數不等式與所求不等式形式相結合投石問路構造新函數，有些表面上看似復雜，但若用整體的思想看待問題，抓住本質，問題就迎刃而解了.而基于例題的變式又是將解題的關鍵由點及面、舉一反三的效果，真正訓練了學生的感悟深度和效度.

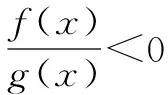
變式設f(x)是R上的奇函數，在區間(-∞，0)上有xf′(x)+f(x)<0且f(-2)=0，求不等式xf(x)<0的解集.

分析例2中突破口是f′(x)g(x)>f(x)g′(x)，移項后得f′(x)g(x)-f(x)g′(x)>0.

例2的變題中有xf′(x)+f(x)<0，根據求導的乘法法則自然會構建函數h(x)=xf(x),構建的函數完全與所求不等式xf(x)<0吻合.

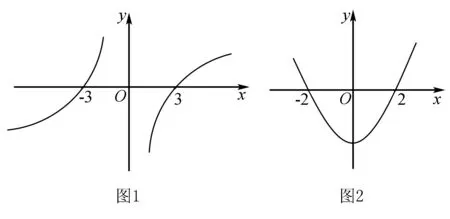
解析構建函數h(x)=xf(x)，在(-∞，0)上有xf′(x)+f(x)<0,則h(x)=xf(x) 在(-∞，0)是單調減函數，且由f(x)是R上的奇函數得h(x)在R上為偶函數，由f(-2)=0得到h(-2)=0.有了函數的單調性及奇偶性，不妨畫出函數好h(x)圖象(如圖2)，得xf(x)<0的解為(-2,2).

總結例2及其變題都是以乘法、除法的求導法則為突破口構建相應函數.我們要通過問題的形式讓學生自發地總結求導的一般特點和一般方法，讓學生在感悟中總結，總結中提升.

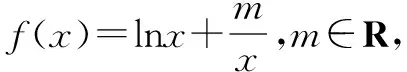
分析本題將不等式f(x2)-f(x1)f(x2)，那么f(x)就是在這個區間上的減函數)，不妨構建g(x)=f(x)-x.

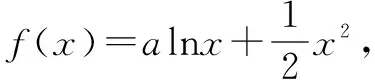
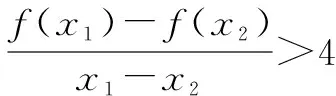
總結例3及其變式都是緊緊抓住函數單調性的定義，因為題目中涉及x1，x2，所以比較自然地聯系函數的單調性的定義，根據定義把已知進行條件變形，那么構建函數也就不難了.

構造函數本就是解決問題的一種技巧，它考查了學生的觀察和動手能力，本文通過三個例題講述了在導數知識中需要構建函數解不等式問題.但是用構建函數解不等式或證明不等式的題目大量存在，還需要學生進一步思考和總結.