介數中心性和黃金分割理論在室內木質門參數化設計中的應用*

鄭小蓉 陳星艷 彭思立 陶 濤

[1.中南林業科技大學, 湖南 長沙 410014；2.美宅科技（北京）有限公司,北京 100089]

近年來隨著房地產業的興起，室內木質門也進入了高速發展階段[1]。根據中國林產工業協會數據，我國木門需求主要來自商品房、保障性住房、二次裝修等，并已形成珠三角地區、長三角地區、東北三省、西北地區和西南地區五大室內木質門產業集群[2]。在實際的設計和生產中，根據門洞尺寸，可將室內木質平開門分為單開門、子母門和對開門三類[3]。由于國內門洞的尺寸標準不統一，木門設計通常采用參數化設計[4]。目前在木門的參數化設計中，可變參數大多較為單一，這雖然有利于節約成本和降低生產難度，但存在尺寸變化后比例失調和美觀度下降等問題。分析變型零件尺寸參數的傳遞路徑[5]，解決家具產品零部件之間因個別零件尺寸變化而產生的尺寸約束沖突問題，是參數化設計在家具產品設計中廣泛運用的關鍵[6]。本文將介數中心性理論和黃金分割比例理論應用于木門的參數化設計，為木門參數化設計提供理論與應用參考。

1 理論基礎簡述

1.1 參數化設計

“參數化” 一詞來源于數學中的參數方程，是指使用某些可以編輯的參數更改系統的最終結果。2005 年，英國設計師扎哈在設計德國費諾科學中心時，采用復雜的型面結構，為使工程師快速得到計算結果，首次將參數化設計軟件引入建筑行業[7]。如今，參數化設計已廣泛應用于工業產品設計[8]。為滿足市場個性化、模塊化和大批量生產需求[9]，設計師通過參數化技術使模型建立更快捷高效，設計實體更精準安全。

1.2 介數中心性

介數中心性（Betweenness Centrality）由美國社會學家Linton C. Freeman提出。節點的介數中心性是指網絡中所有最短路徑中經過該節點的路徑占所有節點對的最短路徑總數的比例[10]。該項指標表明信息傳播到該節點的可能性[11]，節點v的介數中心性可表示為：

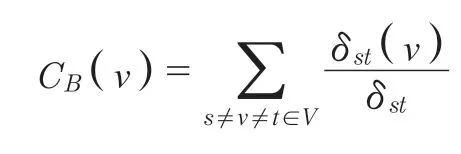
式中：V代表節點集，s、v、t代表合集V中的不同節點，CB(v)代表節點v的介數中心性數值，δst（v）指節點對（s，t）之間的最短路徑經過節點v的條數,δst指節點對（s，t）之間最短路徑的條數[12]。介數中心性可表示某個節點在整個網絡模型中的重要性，主要應用于社交網絡的關系評估[13]。在產品設計的參數化尺寸變形中，介數中心性數值可代表某個零部件對整個產品的重要程度。

1.3 黃金分割比例

比例是一種量度的比率關系，它包含某一個事物的整體與局部之間、局部與局部之間的關系[14]。黃金分割由古希臘數學家歐幾里德提出，指事物之間各部分的數學比例關系, 較大部分與較小部分之間的比值是1∶0.618[15]。黃金分割比例廣泛應用于工業設計、雕刻和建筑等領域，被公認為最具有審美價值的比例數值[16]，可以在設計中從理性的角度賦予產品一定的美學價值[17]。

2 在室內木門參數化設計中的應用

2.1 木門參數化設計流程

在木門參數化設計中，一般設計流程如圖1 所示。1）通過輸入的門洞尺寸判斷門的類型。木門類型由門洞尺寸決定，尺寸約束為單開門寬度：700～999 mm；子母門寬度：1 000～1 333 mm；對開門寬度：1 400～ 1 899 mm；高度統一為1 800～2 400 mm。2）確定木門類型后，分析零部件的組成，選取影響平面造型的零部件，建立零部件模型。3）計算模型網絡中各個零部件的介數中心性數值，作為尺寸變形的參考依據。4）根據黃金比例設置零部件的比例約束，以保證產品整體比例的協調與美感。5）根據實際和工藝情況進行調整，確定最終模型的尺寸。

圖1 參數化設計流程Fig.1 Parametric design process

2.2 建立木門零部件參數模型

室內木門的部件可分為門套、門扇和五金配件[18]。其中門套包括口線、口線底座、門套板、門檔板、密封條等，門扇包括上冒、中冒、下冒、左右門梃、上下門芯、造型線條等，五金配件包括拉手、鎖具、鉸鏈、門吸、密封條、緊固件、貓眼等[19]。

木門零部件參數可分為不變參數、可變參數、導出參數和約束參數[20]。在本模型中，不變參數為木門厚度，其中門套深度尺寸由墻體厚度決定，門扇厚度由各門款的功能和造型決定；可變參數為門的寬度和高度；導出參數為各個零部件的定位尺寸，由零部件定形尺寸和縫隙決定；約束參數包括尺寸約束和比例約束[21]。

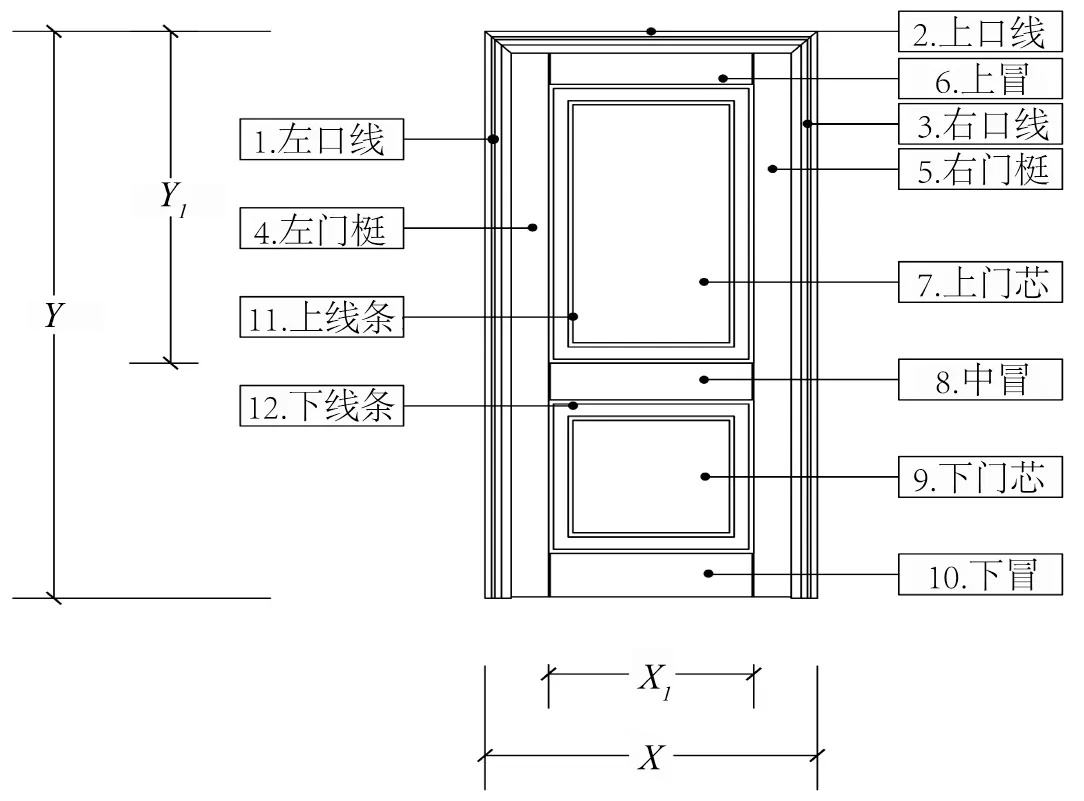
圖2 零部件參數模型圖Fig.2 Drawing of part notes

本文以單開門為例，提取對木門參數化造型有影 響的可變參數和約束參數進行分析，建立的木門零部件參數模型如圖2 所示。

2.3 確定木門模型零部件尺寸形變優先級

將圖2 的零部件參數模型繪制成零部件關系網格，如圖3 所示。根據介數中心性計算出各個節點的介數中心性數值，數值大小代表各個節點對于整體的重要性，是參數化設計的初步依據。以節點2 為例，其作為路徑（1,3）,（4,5）,（1,6）,（3,6）,（3,4）和（1,5）的最短路徑節點，CB(v)的值為1、1/6、1/2、1/2、1 和1 之和，即節點2 的介數中心性數值為4.17。將關系網格模型導入Gephi軟件中，可計算出其他節點的介數中心性數值，計算結果如表1 所示[22]。

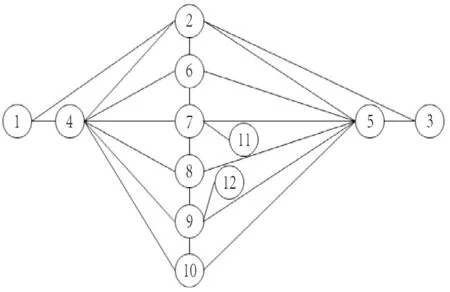
圖3 零件關系網格圖Fig.3 Diagram of part relationship grid

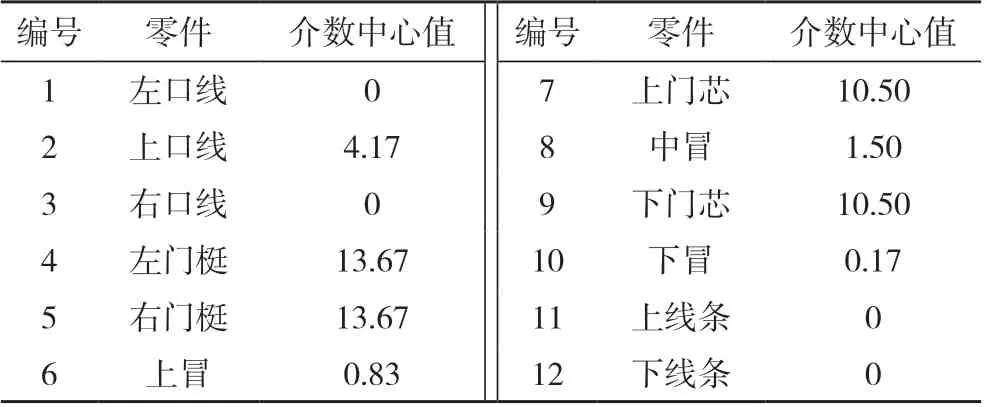
表1 零件的介數中心性數值表Tab.1 Table of intermediate centrality values of parts

使用數據可視化軟件Power-BI將介數中心性表格繪制成零件關系網格圖如圖4 所示，在圖中圓點表示零件，圓的半徑越大則零件的介數中心性值越大，該零件在產品整體中越重要；圓點之間的連線粗細表示兩個零件的接觸面積，連線越粗，表示兩個零件的接觸面積越大，即它們之間的相互影響力越大；相同顏色和粗細的線代表同一類連接線[23]。

在Power-BI的網格圖中拖拽某一節點，與其關聯的其他節點也會被拖拽。圖5 為零件拖拽對比圖，圖5a拖拽的是右口線，可見產品整體受到的影響較小；圖5b拖拽的是右門梃，產品整體受到的影響較大。可以直觀地看到不同介數中心性數值的兩個零件的變化對產品整體產生的影響具有明顯差異。在參數化設計中，不同零件的尺寸變形對于其他零件和產品整體的影響力與零件的介數中心性數值成正相關[24]。

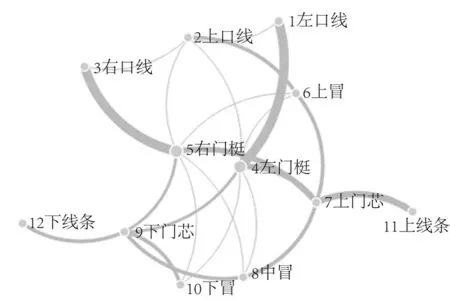
圖4 零件的介數中心性數值網格圖Fig.4 Graph of the numerical grid of the part's centrality

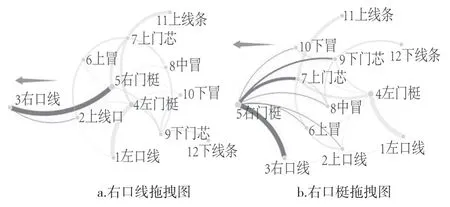
圖5 網格零件拖拽對比圖Fig.5 Diagram of drag and drop comparison of mesh parts

2.4 設置零部件比例約束

為保持木門造型的比例美，在參數化設計時，不能按照單一的理性理論進行尺寸變化，應設置一定的比例約束，以防止尺寸變形導致門比例失調。本文按照黃金分割比例將門扇的寬度和高度各設置一個比例，寬度方向為X1=0.618X，高度方向為Y1=0.618Y，詳見圖2 中的尺寸標注。

2.5 輸出參數化設計模型與對比分析

此款木門的默認尺寸為860 mm ×2 000 mm，是該門款中的常規尺寸。但在實際中建筑門洞尺寸大小不一，因此假設門洞尺寸為單開門的最大尺寸 999 mm ×2 300 mm。在進行參數化設計時，如果按照傳統做法只改變單一的零部件尺寸（如門芯的尺寸），效果如圖6a所示，x軸方向有上下門芯進行拉伸，y軸方向僅有上門芯進行拉伸。存在的問題是上下門芯的比例略有失調，左右兩側門梃比較單薄，對門整體的視覺效果沒有形成很好的支撐作用，產生一種不穩定感。如果按照介數中心性數值的占比對各零部件進行尺寸變形，效果如圖6b所示，根據各個零件在整體的重要性進行尺寸變形，與圖6a相比y軸上的尺寸變形得到較好的調整，但由于左右門梃的介數中心性數值過大 ，使得x軸上出現與圖6a相反的情況，即左右門梃的寬度太大，擠壓門芯空間，使門的整體造型顯得厚重呆板。圖6c是在圖6b基礎上，按照黃金分割比進行調整后的效果，可以看出，與前兩個參數化設計變形結果相比，圖6c中的產品整體更和諧，零部件之間的比例恰當，是較為美觀的設計[25]。

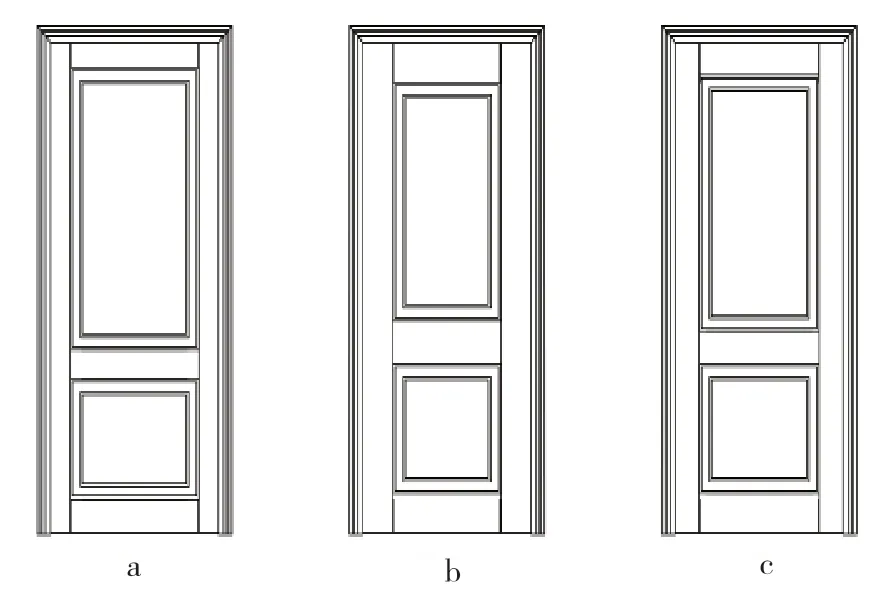
圖6 參數化設計對比圖Fig.6 Parametric design comparison chart

該門款是經典簡單的木門款式，因此在生產中會采取統一的口線橫截面。在上述參數化設計過程中表1 的上口線數值，在實際應用中可設置為0，以保持整體造型的統一。如果門款的造型比較復雜，上口線也可以不與左右口線保持一致的橫截面，單獨設計上口線的造型。該案例僅討論單開門的參數化設計情況，子母門和對開門的零部件比單開門多，情況更為復雜。同樣，造型、零部件和紋樣設計比較復雜的門款也會給參數化設計增加一定的難度，但也可以按照本案例中提出的參數化變形思路和操作步驟，根據門款本身的造型和工藝，進行產品尺寸的參數化設計。

3 結論

本文針對木門參數化設計中存在的變形比例失調問題，對木門參數化設計進行優化：1）引入網格模型的介數中心性理論，將木門結構進行拆分，建立影響平面造型的零部件網格模型。根據模型確定各零部件的參數化變形優先級，作為木門參數化設計流程中的首次尺寸變形依據。2）根據黃金分割原理設置比例約束，對首次尺寸變形的產品進行二次修改，使產品比例和諧并富有美感。3）根據門款的實際造型和工藝，對二次修改的產品進行尺寸調整，輸出最終產品方案。使用改進后的創新流程進行木門參數化產品設計，可增加產品美感，但同時也會增加成本。

工業產品的設計是理性與美學、理論與實踐相結合的產物。在實際設計中，根據門款樣式對零部件的布局進行分析，將理論應用于實踐中，才能設計出滿足市場需要和用戶審美需求的產品。