基于GPU的多相信道化算法效率分析與應用

陳永強，馬 宏，黨宏杰，焦義文，劉燕都

(1.航天工程大學 電子與光學工程系，北京 101416；2.北京通信與跟蹤技術研究所，北京 100094)

0 引言

多相濾波器組(Polyphase Filter Bank, PFB)是數字信號濾波抽取的一種高效實現結構，利用該技術可將串行的信道化過程分解為并行的多路處理流程，從而提高數字信號處理效率[1]。1991年,SETI首次將PFB引入射電系統并使用該技術設計了頻譜分析儀[2]，此后，PFB被越來越多地用于信號處理數字后端，目前國際上多個重要系統均使用了PFB技術進行觀測頻譜的信道化[3]。

20世紀60年代,美國Geraid.Estrin[4]率先提出可重構計算(Reconfigurable Computing)概念。該技術核心思想在于，在通用平臺上通過系統軟硬件結構的靈活重構實現不同的功能[5-6]。圖形處理器件(Graphic Processing Unit, GPU)由于具有眾多的運算核心，特別適合于大量數據的并行處理，2007年NVIDIA提出的計算統一設備架構(Compute Unified Device Architecture, CUDA)從軟件和硬件層面大大簡化了基于GPU的系統開發流程，使得GPU在通用計算領域得到更為廣泛應用。當前，由于GPU相較于FPGA能夠實現較高的頻譜高分辨率且具有更高的可重構性和擴展性[4]，基于CPU+GPU的異構信號處理系統在射電天文[7-8]、雷達[9-10]、無線通信[11-12]等眾多領域成為研究熱點。

隨著基于GPU的高性能計算(High Performance Computation,HPC)技術的快速發展，基于GPU的PFB系統研究逐漸受到研發人員的重視。2011年，麻省理工學院Haystack天文臺的Mark[13]使用NVIDIA Tesla C2050 GPU設計了一款用于VLBI 數字采集系統RDBE的PFB系統，驗證了用GPU替代現有的FPGA板信號處理系統的可能性。測試結果顯示，系統實時數據處理速率達到890 MB/s，而且隨著GPU技術的進一步發展，系統的處理能力將進一步提升和擴展。2014-2016年，馬里蘭大學的Scott C. Kim等研究了基于GPU的多載波系統低延遲多速率重信道化器[14-16]和寬帶接收機[12]，該團隊利用GPU多層次線程結構和存儲結構對PFB的實現進行了優化，采用時域卷積和高維線程模型，在數十兆赫茲帶寬內實現了2G、3G和4G無線電通信信號的高效信道化，系統具有設計靈活、軟件重構、低延遲和高數據吞吐量等優點。2017-2018年，Simon Faulkner等基于GPU開發了一款射頻頻譜感知截獲系統，并為該系統研發了信道化設備[17-18]。該系統采用多相濾波結構實現寬帶信號的信道化接收，采用CUDA stream對流程進行了并發優化。最終，系統處理帶寬達到500 MHz帶寬，可實現1.333 Gs/s采樣率的實時信道化處理能力。該文獻提出的信道化器是一種比較成熟的PFB結構。2017年，新疆天文臺[8]為其觀測系統設計了基于GPU的多相濾波系統，為GPU在國內數字后端應用進行了有效的探索。

在多相濾波系統中，FIR濾波環節由于涉及大量數據的乘加運算，是影響系統效率的關鍵因素。當前，在GPU平臺上FIR濾波算法的實現方式主要分為頻域濾波算法[19]和時域濾波算法[20]2種。文獻[21-22]給出了基于FFT的頻域FIR濾波方法的實現方式，得到了較好的加速比,同時對比了GPU、Intel-ipps和FFTW三個平臺上長序列頻域濾波效率，證明Intel-ipps性能略優于FFTW。而Scott C. Kim[12]、Mark[13]及Jayanth Chennamangalam[23]等均從時域實現了多相濾波過程，給出了時域FIR在連續信號濾波中的應用。以上文獻分別從時域和頻域給出了長序列FIR濾波的優勢和實現方法，卻沒有給出在不同的應用場景下2種濾波算法的適用條件。另外，近年來，在基于FPGA的平臺上，基于DA法[24-25]和查找表法[26]等多種優化方法的高效并行FIR濾波方法研究取得豐碩成果，但這些方法難以直接移植到GPU平臺。

本文首先介紹了基于多相濾波技術的并行信道化算法，并分析了其運算效率；然后對運算過程中耗時最長的多通道并行濾波過程進行了分析，基于CUDA流式架構分別設計了基于時域卷積和頻域快速卷積的FIR濾波算法，并分析了2種算法在多相信道化結構中的性能；最后基于GPU平臺設計了多相信道化實現方法并用實驗驗證了分析的正確性。

1 基于多相濾波技術的并行信道化算法

典型的K通道并行信道化算法低通濾波實現原理框圖如圖1所示[27]。

圖1 多通道基帶轉換原理框圖Fig.1 Block diagram of multi-channel baseband conversion

圖1中，各信道中心頻率為ωk=2πfk/fs，由于實際處理過程中所用均為實信號，因此本文重點針對實信號進行分析。設經過D倍抽取后,輸出采樣率為fs2=fs/D，采樣周期Ts2=DTs1，在實信號模式下，該結構第k通道數學表達式為：

yk(mTs2)=x1(nTs1)e-jωkn*hLP(nTs1)|n=mD|=

(1)

為了提高運算效率，對濾波過程進行多相分解，將濾波器分解為并行的K路，每一路分支濾波器長L=[N/K]。原型低通濾波器索引i可分解為：

i=qK+p，

(2)

式中，q為每一路分支濾波器內部點數索引，q=0,1,2,…,L-1；p為分支濾波器索引，p=0,1,2,…,K-1。可得：

(3)

令hp(m)=hLP((mK+p)Ts1)表示第p路分支濾波器，xp(m)=x1[(mD-p)Ts1]表示并行分路后第p路輸入信號。式(3)可改寫為：

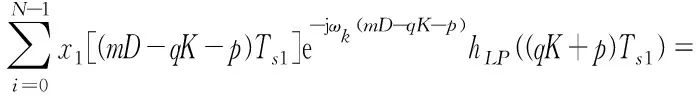
(4)

令h=K/D，i=q,l=qh,則有：

(5)

(6)

此時，實際上按照多相分支濾波器架構完成了中心頻率為ωk的射頻信號的單通道信道化濾波接收。由于各通道均勻劃分，可令ωk=2πk/D，濾波器截至頻率為π/D，則第k通道信道化后的信號可表示為：

(7)

式中，為了最大限度提高處理效率，降低每個通道的數據速率，令抽取倍數D等于通道數K，即可得到最大抽取的DFT濾波器組：

(8)

式(8)即為最大抽取DFT濾波器組的經典多相信道化結構的數學表示，也是干涉測量基帶轉換器、射電天文數字后端等系統常用信道化算法。該算法本質是多通道并行分支濾波和多路DFT，DFT可用其快速算法FFT實現，因此多路分支濾波運算效率成為制約該結構實時性的主要因素。由式(8)可知，分支濾波過程本質上仍然是多路FIR濾波過程，而對于長度為L的輸入序列x(n),n=0,1,…,L-1和長度為M的FIR濾波器h(n),n=0,1,…,M-1，FIR濾波過程可用如下線性卷積關系表示：

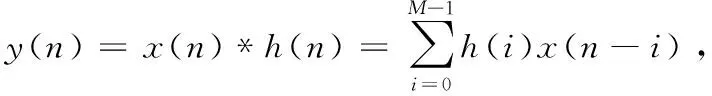
(9)

式中，y(n)為線性卷積輸出，其長度為L+M-1。此時，問題轉化為長序列FIR濾波的高效實現。

2 基于CUDA的長序列實時FIR濾波方法研究

在實際工程實踐中，由于輸入信號過長無法一次處理，通常需要做分段處理，但由于卷積運算本身特殊性，分段處理時在每一段數據兩端位置將出現結果異常。為解決這一問題，研究者提出基于重疊相加法和重疊保留法[28]的長序列FIR濾波連續方法。馬里蘭大學的Kim等[12]利用卷積算法和重疊保留法在CUDA平臺上實現了高效濾波運算，設計了基于GPU的寬帶信道化接收機。為了提高卷積運算的效率，文獻[21-22]也提出了重疊相加法和頻域卷積相結合的快速濾波方法，并給出了該方法在CUDA平臺上的應用效果。本節將重點根據并行信道化運算需求，設計適用于本文架構的高效濾波方法。

2.1 典型長序列濾波算法

為了實現長序列的連續濾波，需要對輸入數據分段進行運算。而根據分段處理方法的不同，常用的長序列濾波方法分為重疊相加法和重疊保留法[29]。2種算法實現流程如下。

2.1.1 基于重疊相加法的長序列分段濾波方法

設長為N，輸入數據x(n)每一段處理長度為L，濾波器h(n)階數為M-1，那么該算法的執行流程為：

① 將輸入數據分段，每段長度為L；

② 計算第1段數據與h(n)的卷積，得到濾波結果y0(n)長度為L+M-1；

③ 計算第2段數據與h(n)的卷積，得到濾波結果y1(n)長度為L+M-1；

④ 將y1(n)與y0(n)拼接作為輸出，并使得y1(n)的前M-1點與y0(n)的后M-1點重疊相加；

⑤ 以拼接結果作為新的y0(n)并重復以上兩步，直到分段數據處理完畢。

2.1.2 基于重疊保留法的長序列分段濾波方法

設長為N，輸入數據x(n)每一段處理長度為L，濾波器h(n)階數為M-1，那么該算法的執行流程為：

① 將輸入數據分段，每段長度為L；

⑥ 以y0(n)，y1(n)，y2(n)，…的順序拼接結果即可得到濾波輸出。

重疊相加法的優勢在于對輸入數據的操作簡單，在分段方法確定后即可直接進行卷積運算，流程清晰，但完成卷積運算后各段結果數據之間增加了加法操作。重疊保留法需要對輸入數據進行M-1點的循環拷貝，增加了數據傳輸的壓力，但其輸出數據直接為最終結果，無需額外操作。2種方法雖略有區別，但其綜合運算復雜度相當[30]，本文選擇重疊保留法作為數據處理方法。

2.2 基于GPU的多通道并行時域濾波方法

由式(9)可知，對一個時間序列做FIR濾波本質上就是將該信號與濾波器單位沖激響應做線性卷積。輸出信號實際上是以濾波器單位沖擊響應為權值，對輸入信號滑動求取加權和。在實時信號處理中，這一過程可以通過重疊保留法予以實現。GPU架構下基于重疊保留法的多通道并行FIR實現過程如圖2所示。

圖2 基于重疊保留法的時域FIR濾波流程Fig.2 Time-domain FIR filtering process based on overlap preservation method

GPU架構下基于重疊保留法的長序列時域FIR濾波流程如下：

① 設參與濾波的數據為k路，定義并啟動k路CUDA stream，保證每一個stream對應處理一路數據；

② 在每一個stream內，將輸入采樣信號x(n)用重疊保留法分塊為xi(n)，分塊后每一段數據大小為L，濾波器長度為M，然后將第1段數據前向擴展M-1個點，使得其中擴展后數據長度為L+M-1；

③ 利用線性卷積分別計算第1段前L次滑動卷積過程，將L點結果輸出至顯存；

④ 將上一段后M-1點數據拷貝到下一段數據頭部重新組成L+M-1點數據；

⑤ 重復③、④兩步，計算每一段分塊數據時域濾波結果yi(n)；

⑥ 將yi(n)各段拼接整合，提取出整段數據最終的濾波結果。

2.3 基于GPU的多通道并行頻域濾波方法

由傅里葉變換的原理可知，2個序列的DFT的乘積相當于該序列時域做循環卷積(或圓周卷積)。而根據文獻[33]利用圓周卷積無混疊計算線性卷積的條件是，輸出信號y(n)至少需要N點DFT，N≥L+M-1，即：

Y(k)=X(k)H(k),k=0,1,...,N-1，

(10)

式中，X(k)，H(k)對應于x(n)和h(n)的N點DFT。由于輸出信號y(n)的N點DFT一定可以在頻域表示該信號，故利用DFT先求的輸入信號和濾波器系數的N點DFT，然后在頻域逐點相乘得到乘積序列Y(k)，最后對Y(k)求N點DFT得到的圓周卷積，該圓周卷積結果等于x(n)和h(n)的線性卷積，即：

y(n)=x(n)*h(n)=IDFT[X(k)H(k)]=

IDFT[Y(k)]，

(11)

式中，k=0,1,...,N-1；n=0,1,...,N-1。

以上方法給出了利用DFT實現線性卷積的過程，從公式和數據處理流程上看，與時域直接卷積方法相比，該方法增加了信號和濾波器系數時域擴展、DFT運算、頻域乘法運算以及IDFT運算，流程更加復雜，但是與復雜的卷積運算相比，DFT和IDFT可以通過快速算法得到所需信號，極大地提高了運算效率。基于重疊保留法的頻域FIR實現過程如圖3所示。

圖3 基于重疊保留法的頻域FIR濾波流程Fig.3 Frequency-domain FIR filtering process based on overlap preservation method

GPU平臺上基于重疊保留法的頻域快速卷積算法流程如下：

① 設參與濾波的數據為k路，則定義并啟動k路CUDA stream和FFT句柄，并將Cufft句柄綁定到stream；

② 將輸入采樣信號x(n)分段，第i段為xi(n)；每一段數據長度為L，濾波器h(n)長度為M;

③ 將每一段數據xi(n)和濾波器系數h(n)擴展為L+M-1位。其中數據向前擴展M-1位，即在x0(n)前M-1位補零，此后在xi(n)前M-1位補xi-1(n)的后M-1位；在h(n)后向擴展L-1位并補零；

④ 利用Cufft庫函數計算分段數據L+M-1點FFT，Xi(k)=FFT[xi(n)]，同時對濾波器也做相同點數的FFT，Hi(k)=FFT[h(n)]；

⑤ 將經過FFT運算的數據Xi(k)和濾波器系數Hi(k)對應相乘，得到每一段數據的濾波結果的頻譜，Yi(k)=Xi(k)Hi(k)；

⑥ 對濾波結果的頻譜做L+M-1點FFT，yi(n)=IFFT[Yi(k)]，即可得到分段數據長度為L+M-1的線性卷積結果yi(n)；

⑦ 將yi(n)中后L點數據取出并按順序拼接，即可得到整段數據的濾波結果。

2.4 2種濾波方法對比分析及實現

基于重疊保留法的頻域濾波過程有效利用了FFT算法優勢，在長序列高階濾波過程中加速效果明顯。然而，該方法將原本簡單的乘加運算關系變成了變量擴展、分段FFT、相乘、分段IFFT等多個步驟，增加了流程的復雜度，給流程的調度帶來了額外的開銷，而且在濾波器階數較少的情況下，在重疊部分需要額外增加大量的內存操作和運算，這些操作將直接影響算法性能；另外，為了使用FFT算法加速運算過程，數據長度也需滿足2的整數次冪的要求。與之相比，時域濾波方法由于簡單直接，在低階運算中將具有更優的應用效果，但卷積運算本身的復雜性將導致時域算法在高階濾波運算中效率急劇下降。下面用仿真方法對2種算法的運算復雜度進行分析。

設每一路輸入數據分段長度為L，濾波器系數長度M，基于重疊保留法的時域和頻域濾波算法的計算復雜度根據卷積和FFT算法的不同而有較大差異。下面以2種算法中耗時較長的乘法計算次數為參考，分析2種算法的運算復雜度。

2.4.1 時域卷積算法

在基于重疊保留法的時域濾波算法中，直接卷積運算將需要2×L×M次乘法運算；由于數據前向擴展M-1點，共增加約M(M-1)次乘法運算。所以采用基于重疊保留法的時域濾波算法需要的乘法運算次數為：

N=2ML+M(M-1)=M(2L+M-1)。

(12)

當數據長度與濾波器系數相當，即M≈L時：

N≈3L2。

(13)

當數據長度遠大于濾波器系數，即M?L時：

N≈2ML。

(14)

對比式(13)、式(14)可知，當濾波器階數較少時，時域方法乘法運算量與數據長度近似成線性關系。隨著濾波器階數的增加，運算復雜度急劇增大，當濾波器階數與數據長度相當時，乘法運算量與數據長度近似成平方關系。由此可見，時域卷積方法在低階條件下將具有更大的優勢。

2.4.2 頻域卷積算法

當采用頻域濾波算法時，需要首先對數據和濾波器系數進行擴展，使得2路數據長度均達到L+M-1點，然后對2路擴展數據做FFT運算，則FFT運算實際乘法運算次數為：

N=4×[(L+M-1)/2×lb(L+M-1)+(L+M-

1)/2×lb(L+M-1)]=

4×[(L+M-1)lb(L+M-1)]。

(15)

2個序列相乘需要經過L+M-1次乘法，得到L+M-1個結果，再對L+M-1點數據進行IFFT運算，需要2×[(L+M-1)lb(L+M-1)]次乘法。由此可知，采用頻域卷積需要的乘法次數為：

N=6×(L+M-1)lb(L+M-1)+(L+M-1)=

(L+M-1)[6lb(L+M-1)+1] 。

(16)

當數據長度與濾波器系數相當，即M≈L時：

N= 2L[6lb(2L)+1]。

(17)

當數據長度遠大于濾波器系數，即M?L時：

N≈L[6lbL+1]。

(18)

2.4.3 2種算法對比

從以上分析可以看出，時域濾波方法過程簡單，當濾波器階數較少時，運算效率較高；但受卷積運算影響，當濾波器階數較大時，單次運算量過大，難以滿足要求。而頻域濾波方法充分利用了FFT運算的高效結構，能夠明顯降低乘法運算次數，而且隨著濾波器階數的增加和處理數據點數的增加，這種優勢將更加明顯；但頻域濾波方法在運算過程中需要對參與運算的濾波器系數和輸入數據進行擴充，并在擴充的基礎上開展2次FFT運算、一次逐點乘法運算和一次IFFT運算，給運算過程帶來額外的負擔，而且這種負擔在濾波器階數較低時將更為顯著。

為了對時域和頻域濾波方法在不同數據條件下的性能進行定量分析，本文通過實驗對2種方法的性能進行了驗證。輸入仿真數據長度為L為1 024點，濾波器系數序列點數M分別選擇4，8，16，32，64，128，256，512，1 024。如此參數設置將確保仿真過程能夠涵蓋從M?L到M≈L的整個范圍，從而對2種算法的性能進行全面的分析。

仿真結果如圖4所示，設N為運算量，M為濾波器系數個數，L為輸入數據總長度。圖中藍色曲線表示時域卷積算法在不同濾波器系數M條件下運算量N隨著輸入數據總點數L的變化關系。綠色曲線表示頻域卷積算法在不同M條件下N隨著L的變化關系。圖中ConvM和fftM分別表示濾波器系數為M時，時域卷積和頻域濾波算法的運算量。

圖4 時域卷積和頻域卷積性能對比Fig.4 Performance comparison between time-domain convolution and frequency-domain convolution

從仿真結果可知：

① 隨著濾波器階數的增加，時域濾波方法的運算量隨著處理數據點數的增加而迅速增大，與之相反，頻域濾波方法在M值增加的過程中運算量并未出現劇烈變化。由此可知，在濾波器階數較大的條件下，頻域濾波算法具有較為明顯的優勢，而且這種優勢隨著M值的增加而更加明顯，這與上文分析一致。

② 在濾波器階數與數據長度相當時，頻域卷積算法得優勢最為明顯。

③ 在M值與L值相比明顯較小時，頻域濾波方法的不足隨著M值的減小而越發顯著。在本文仿真條件下，當M值等于或小于16時，頻域濾波方法在不同數據長度時的運算量和運算量增加速率均明顯高于時域算法。

④ 當L值在1 024量級，M=32時，時域和頻域2種卷積方法的計算量相當，且頻域算法計算量增加速率更快。因此，在一次處理的輸入數據較大而M不大于32時，時域算法的運算量將低于頻域算法。

綜合以上仿真結果分析，在長序列實時濾波運算中可得出如下結論：

① FIR濾波器階數是影響卷積運算效率的主要因素，數據分段方法在一定條件下可以影響運算效率；

② 更高的濾波器階數只有與之相當的數據長度時才能體現頻域濾波的高效率優勢，即當濾波器階數較高時，數據段的長度最佳選擇是與濾波器階數相當；

③ 當濾波器階數較小，小于或等于16時，無論分段長度多長，時域濾波效率均優于頻域濾波效率。且在此條件下，為了減少分段處理時額外的數據拷貝消耗，更長的數據分段長度將更有利于濾波運算效率的提升。

在信道化運算過程中，各路濾波器為原型濾波器多相分解之后的序列，其長度將是M/D，其中D為多相分支的路數。在寬帶數據處理中，為了最大限度降低信號速率，一般會選擇較大的D，這將導致每一路分支濾波器階數的降低。若原型濾波器長度為256，分路數D為16，則每一路分支濾波器長度即為16，在此條件下選擇時域濾波算法將是最優選擇，而每次處理的信號長度盡可能大將有助于提升數據處理效率。

3 實驗驗證

基帶轉換器是VLBI系統數字信號采集和處理的核心裝備，其主要功能是為后端處理系統提供多通道的基帶信號。由于干涉測量系統需要利用帶寬綜合技術對大帶寬內的多個子帶進行處理，因此要求基帶轉換器能夠對寬帶信號進行信道化處理，為后端處理系統輸出所需的子帶信號。多相信道化算法由于其高效優勢在基帶轉換器的實現過程中得到了廣泛應用，目前國際主流基帶轉換器均采用該算法進行寬帶信號的實時處理。

為了驗證以上分析結果的正確性，按照式(8)的分析結果，設計了基于GPU的VLBI多相信道化器。設每個分支濾波模塊輸入信號x(n)長度為L，對應的FIR分支濾波器系數序列h(n)長度為M，則基于CUDA的分支濾波算法流程如圖5所示。

圖5 分支濾波算法流程Fig.5 Block diagram of branch filtering algorithm flow

圖中分支濾波模塊是整個信道化模塊中運算量最大的部分，每一個分支濾波器是一個獨立的濾波運算單元，完成輸入數據和濾波器系數的卷積運算。在多項濾波實現中，各通道輸入數據和濾波器系數均已經通過多相分解實現了并行化，將各通道數據與運算流程解耦合，使得各通道數據在處理過程中相互獨立。而在各通道內部，輸入數據與分支濾波器通過卷積運算實現濾波操作。

由圖5可以看出，輸入數據被分成并行的D路，原型濾波器也做相應的多相分解，使得分支路數也為D，然后根據分支路數啟動D路并行的CUDA stream。每一路數據的運算過程發生在各自的CUDA stream內，這種設計一方面充分利用了各路數據的并行性，使得各路數據處理流程在stream之間完全獨立，消除了因串行等待造成的時間延遲；另一方面采用這種方法有效合并了各路數據的內存訪問，解決了因內存讀取不連續造成的效率降低下的問題。

由式(9)可知，在每一個CUDA stream內，實際上進行的是M點濾波器系數和L點輸入數據的線性卷積運算，而對于一個輸出點而言，卷積運算本質上是2個M點長度序列的逐點對應乘加。在圖5所示的算法流程中，每個線程負責完成M次乘加運算并最終實現一個卷積結果的輸出，所有L個線程并行啟動即可完成所有輸出點的運算。為了降低因運算過程中對濾波器系數反復讀取造成的運算效率損失，利用線程塊的共享內存存儲參與運算的數據和系數。

本文VLBI基帶轉換器基于CUDA10.2和VS2015開發，GPU采用NVIDIA Tesla V100，信道化軟硬件開發設計采用圖2、圖3所示多相信道化結構。輸入數據在信道化入口即按通道數進行串并轉換，劃分為均勻的多路，然后按照通道數啟動CUDA stream對每一之路數據異步并行處理。在時域卷積模式下每一個流內按照圖5所示流程進行分支濾波操作，每一個流內數據處理順序進行，各流之間數據傳輸和核函數的執行異步并發。在各流完成各自操作后，對各通道數據按通道數進行D點FFT，得到并行的多路基帶數據輸出。輸出數據按要求將寬帶信號均勻劃分為D路。

輸入數據采樣率為1 024 Ms/s，信道化輸出16路復信號，每一路帶寬64 MHz。取0.156 25 s原始數據進行測試，即總共數據點數為1 677 216。多相濾波原型濾波器階數255，則每路分支濾波器系數點數為16。分別按照每段數據長度1 024，4 096，65 536，262 144點對原始數據進行分段處理。分別統計每種分段長度條件下時域卷積算法和頻域濾波算法條件下信道化所用時長，結果如圖6所示。

圖6 時域卷積和頻域卷積性能對比Fig.6 Performance comparison of time domain convolution and frequency domain convolution

由圖6可以看出，當濾波器階數為15時，各種數據分段長度下，時域濾波性能均優于頻域濾波性能，且隨著數據分段長度的增加，2種濾波方法性能均明顯增強，這與本文的預測完全一致。但是，受GPU片上資源限制，單次處理的數據長度不可能無限制增加，在數據長度超過65 536點時，算法性能增加速度變慢甚至出現下降。因此，在本文所示信道化運算條件下，以單通道每次處理65 536點數據為最佳設置。另外,從圖6放大部分可看出，2種算法中每一段數據的處理耗時均隨著處理數據長度的增加而近似線性增加，且頻域算法的耗時增加速率明顯高于時域算法，這與本文預測一致。

4 結束語

以干涉測量多相信道化基帶轉換器為應用背景，以基于GPU的通用計算平臺為應用目標，提出一種基于CUDA的多相信道化實現方法，為了提高FIR濾波環節的運算效率，針對信道化算法中運算量最大的分支濾波模塊，利用重疊保留法設計了基于CUDA的頻域濾波算法和時域濾波算法。然后，利用仿真平臺對2種算法的運算復雜度和適用條件進行了分析，結果顯示：

① 時域濾波方法簡單高效，但受卷積運算復雜度影響，單次運算量大，在濾波器階數較低(≤16)且數據速率較高時適用；

② 頻域濾波方法流程復雜，但FFT算法的應用使得運算量大大降低，適用于濾波器階數較大(≥32)的場合。

利用以上分析結果設計了基于GPU的16通道多相信道化算法實現結構，并對該結構進行了測試，結果顯示在各分支濾波器系數長度為16條件下，隨著處理數據點數的增加，采用多通道并行時域卷積算法能夠達到更高的運算效率，與分析結果一致。未來，該分析結果有望為干涉測量系帶轉換器的高效實現提供有效的技術支持。